数学人教A版(2019)必修第一册5.1.2弧度制 课件(共15张ppt)
文档属性
| 名称 | 数学人教A版(2019)必修第一册5.1.2弧度制 课件(共15张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-29 07:38:33 | ||
图片预览






文档简介
(共15张PPT)
高中数学 人教A版 必修第一册 第五章
5.1.2 弧度制
问题1:初中学过哪些度量角的单位?它们之间如何换算呢?
问题2:你知道300+sin300等于多少
吗?
两个不同量之间无法运算.
不同单位之间可以换算.
1吨=1000千克=1000公斤;
1m=10dm=100cm=1000mm.
不同的单位制能给解决问题带来方便.
类比思考,角的度量是否也能用不同的单位制呢?能否像度量
长度那样,用十进制的实数来度量角的大小呢?
环节1:角度制的再认识
问题3 在初中,我们用角度制 度量角,比如直角是900的角.
你还记得10的角是如何定义的吗?
这种用度作为单位来度量角的单位制叫做角度制
实际上,将圆周等分成360份,是古巴比伦
人的创举,据说其渊源与天文学有关.
问题4 如果将圆周等分成其他份数,
是否也可以建立度量角的方式呢?
历史上还有将圆周分成400份的百分制、分成6000份的密位制
等.
环节1:角度制的再认识
互联网、书籍等途径查阅相关文献
资料,知道密位制这种度量角的单位
广泛应用于航海和军事上.但沿用至今
的360等分制,这种分法确实有其优越
性,使用起来比较方便,如因为360的
因数较多,所以一些特殊角都是整数,
很多正多边形的内角都为整数等.
问题5 这些度量角的方式的共同点是什么?
都是将圆周进行等分;要度量角的大小,得先建立1个“单位”的角的
大小.
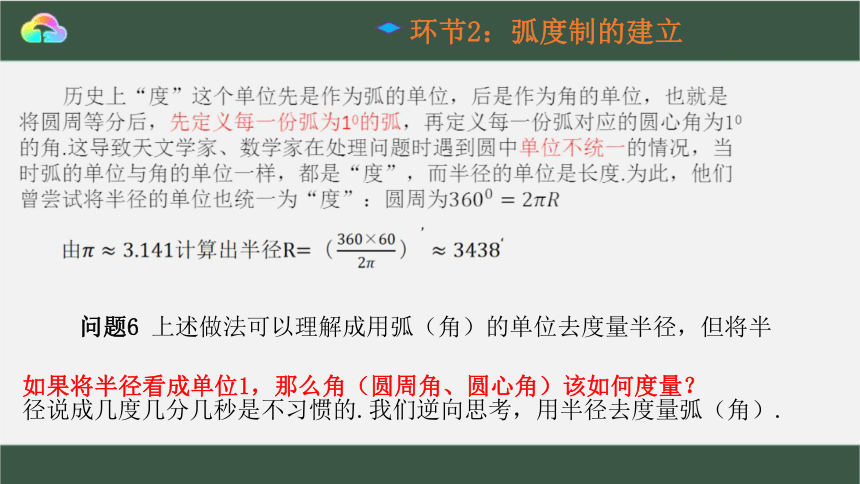
环节2:弧度制的建立
问题6 上述做法可以理解成用弧(角)的单位去度量半径,但将半
径说成几度几分几秒是不习惯的.我们逆向思考,用半径去度量弧(角).
如果将半径看成单位1,那么角(圆周角、圆心角)该如何度量?
环节2:弧度制的建立
弧度制
思想
!
定义:长度等于半径长的圆弧所对的圆心角叫作1弧度的角.
(
环节3: 弧度制的深度认识
弧度单位用符号rad表示,读作弧度. rad是radian的缩写,
radian取自radius(半径)与angle(角),我国曾译作“弪(jìng)
”,取自“弧”和“径”.所以这一新的角的度量单位表明了半径、
圆心角、弧长三者之间的关系.
从感性认知到
理性分析
问题7 你能探究出半径、圆心角、弧长三者的关系式吗
?
(
环节3: 弧度制的深度认识
追问1 圆心角的大小与哪些量有关?请用关系式表示
.
(
环节3: 弧度制的深度认识
圆心角与半径无关.从而可以利
用单位圆直观认识弧度作为角的度量
单位,并用图表示出它.
规定:把半径为1的圆叫做单位圆.
追问4 1弧度的角有多大呢
?
=1rad<60
0
=2rad<1200
(
环节3: 弧度制的深度认识
追问5 当角的终边逆时针旋转时为正角,相应的弧度数为正,当顺时针旋转呢
一般地,正角的弧度数是一个正数,负角的弧度数是一个负数,
零角的弧度数是0.由此我们知道,用弧度(实数)度量了角,弧度
是十进制,而角度是六十进制.
问题8 角度制、弧度制都是角的度量制,它们之间应该可以换算.如何换算呢
?
你认为联系两种度量制的桥梁是什么?
(
环节3: 弧度制的深度认识
从角度到弧度,角的度量单位放大了57倍多.
今后用弧度制表示角时,“弧度”二字或“rad”通
常略去不写,而只写该角所对应的弧度数.
课后请用计算器进行角度与弧度的互化动手操作.
角度与弧度的互化
问题9 请填写下列特殊角的度数与弧度数的对应表:
度 00 300 450
1200 1350 1500
3600
0
弧度
角的概念推广后,在弧度制下,角的集合与实数集R之间建
立起一一对应的关系,每一个角都有唯一的一个实数(等于这
个角的弧度数)与它对应,反过来,每一个实数也都有唯一的
一个角(即弧度数等于这个实数的角)与它对应.
在初等数学和日常生活中人们习惯使用角度制,但在高等数学中引入弧
度制更加便利,如能大大简化微积分中关于三角函数的各种公式,在以后的
高等数学和物理学中大家会感受到弧度制相较于角度制的便利之处.我们通
过一个大家熟悉的例子来看弧度制的优点.
弧度制的应用
问题10 利用弧度制证明下列关于扇形的公式:
证明:
问题11 你能说出角度制与弧度制的异同吗?
基础知识:
相同点:都是通过等分圆周的方式建立的度量角的单位制,
不同点:1.弧度制以长度来度量角,角度制是以角量角;
2.进制不同;3.1弧度是等于半径长的弧所对的圆心角的大小,而10的
角是周角的360分之一,弧度单位比角度单位大了57倍多.
角度制
弧度制
基本技能:
从历史悠久、底蕴深厚的数学文化入手学习弧度制,研究路径由
角度制的再认识——弧度制的建立——弧度制的深度认识——学以致
研究路径:
用.
背景——定义——表示
课后作业: P175练习1、2,习题2、3;
P176拓广探索10、12
高中数学 人教A版 必修第一册 第五章
5.1.2 弧度制
问题1:初中学过哪些度量角的单位?它们之间如何换算呢?
问题2:你知道300+sin300等于多少
吗?
两个不同量之间无法运算.
不同单位之间可以换算.
1吨=1000千克=1000公斤;
1m=10dm=100cm=1000mm.
不同的单位制能给解决问题带来方便.
类比思考,角的度量是否也能用不同的单位制呢?能否像度量
长度那样,用十进制的实数来度量角的大小呢?
环节1:角度制的再认识
问题3 在初中,我们用角度制 度量角,比如直角是900的角.
你还记得10的角是如何定义的吗?
这种用度作为单位来度量角的单位制叫做角度制
实际上,将圆周等分成360份,是古巴比伦
人的创举,据说其渊源与天文学有关.
问题4 如果将圆周等分成其他份数,
是否也可以建立度量角的方式呢?
历史上还有将圆周分成400份的百分制、分成6000份的密位制
等.
环节1:角度制的再认识
互联网、书籍等途径查阅相关文献
资料,知道密位制这种度量角的单位
广泛应用于航海和军事上.但沿用至今
的360等分制,这种分法确实有其优越
性,使用起来比较方便,如因为360的
因数较多,所以一些特殊角都是整数,
很多正多边形的内角都为整数等.
问题5 这些度量角的方式的共同点是什么?
都是将圆周进行等分;要度量角的大小,得先建立1个“单位”的角的
大小.
环节2:弧度制的建立
问题6 上述做法可以理解成用弧(角)的单位去度量半径,但将半
径说成几度几分几秒是不习惯的.我们逆向思考,用半径去度量弧(角).
如果将半径看成单位1,那么角(圆周角、圆心角)该如何度量?
环节2:弧度制的建立
弧度制
思想
!
定义:长度等于半径长的圆弧所对的圆心角叫作1弧度的角.
(
环节3: 弧度制的深度认识
弧度单位用符号rad表示,读作弧度. rad是radian的缩写,
radian取自radius(半径)与angle(角),我国曾译作“弪(jìng)
”,取自“弧”和“径”.所以这一新的角的度量单位表明了半径、
圆心角、弧长三者之间的关系.
从感性认知到
理性分析
问题7 你能探究出半径、圆心角、弧长三者的关系式吗
?
(
环节3: 弧度制的深度认识
追问1 圆心角的大小与哪些量有关?请用关系式表示
.
(
环节3: 弧度制的深度认识
圆心角与半径无关.从而可以利
用单位圆直观认识弧度作为角的度量
单位,并用图表示出它.
规定:把半径为1的圆叫做单位圆.
追问4 1弧度的角有多大呢
?
=1rad<60
0
=2rad<1200
(
环节3: 弧度制的深度认识
追问5 当角的终边逆时针旋转时为正角,相应的弧度数为正,当顺时针旋转呢
一般地,正角的弧度数是一个正数,负角的弧度数是一个负数,
零角的弧度数是0.由此我们知道,用弧度(实数)度量了角,弧度
是十进制,而角度是六十进制.
问题8 角度制、弧度制都是角的度量制,它们之间应该可以换算.如何换算呢
?
你认为联系两种度量制的桥梁是什么?
(
环节3: 弧度制的深度认识
从角度到弧度,角的度量单位放大了57倍多.
今后用弧度制表示角时,“弧度”二字或“rad”通
常略去不写,而只写该角所对应的弧度数.
课后请用计算器进行角度与弧度的互化动手操作.
角度与弧度的互化
问题9 请填写下列特殊角的度数与弧度数的对应表:
度 00 300 450
1200 1350 1500
3600
0
弧度
角的概念推广后,在弧度制下,角的集合与实数集R之间建
立起一一对应的关系,每一个角都有唯一的一个实数(等于这
个角的弧度数)与它对应,反过来,每一个实数也都有唯一的
一个角(即弧度数等于这个实数的角)与它对应.
在初等数学和日常生活中人们习惯使用角度制,但在高等数学中引入弧
度制更加便利,如能大大简化微积分中关于三角函数的各种公式,在以后的
高等数学和物理学中大家会感受到弧度制相较于角度制的便利之处.我们通
过一个大家熟悉的例子来看弧度制的优点.
弧度制的应用
问题10 利用弧度制证明下列关于扇形的公式:
证明:
问题11 你能说出角度制与弧度制的异同吗?
基础知识:
相同点:都是通过等分圆周的方式建立的度量角的单位制,
不同点:1.弧度制以长度来度量角,角度制是以角量角;
2.进制不同;3.1弧度是等于半径长的弧所对的圆心角的大小,而10的
角是周角的360分之一,弧度单位比角度单位大了57倍多.
角度制
弧度制
基本技能:
从历史悠久、底蕴深厚的数学文化入手学习弧度制,研究路径由
角度制的再认识——弧度制的建立——弧度制的深度认识——学以致
研究路径:
用.
背景——定义——表示
课后作业: P175练习1、2,习题2、3;
P176拓广探索10、12
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
