人教版小学数学六年级下册第三单元《圆柱与圆锥》单元练习题(含答案)
文档属性
| 名称 | 人教版小学数学六年级下册第三单元《圆柱与圆锥》单元练习题(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 166.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-29 00:00:00 | ||
图片预览



文档简介
六年级数学下册第三单元《圆柱与圆锥》单元练习题
一、选择题(共7小题,每小题2分,满分14分)
1.计算一个烟筒需要多少铁皮,是求它的( )。
A.侧面积 B.表面积 C.体积 D.溶积
2.下面四种测量圆锥高的方法中,( )是正确的。
A. B. C. D.
3.小明买了一瓶水,喝掉了一部分后还有剩余(如图所示),已知这个瓶子的内直径是。根据图中标出的数据,小明用算式“”计算的是( )。
A.喝掉的水的体积 B.瓶子的容积
C.剩余的水的体积 D.喝掉的水和剩余的水相差的体积
4.一根圆柱形木料的底面半径是,长是。如图所示,将它截成段,求这些木料的表面积比原来增加了多少平方米。列式是( )。
A. B. C. D.
5.一个圆柱形水桶,从里面量直径为,桶深。现将水倒进桶里,水占水桶容积的( )。
A. B. C. D.
6.如图,把一个圆柱切拼成一个近似的长方体,比较切拼前、后的体积和表面积,下面说法正确的是( )。
A.体积、表面积均不变 B.体积变小,表面积不变
C.体积不变,表面积变小 D.体积不变,表面积变大
7.如图,这两个等底等高的容器内的沙子图中阴影部分相比,( )。
A.甲比乙多 B.乙比甲多 C.同样多 D.无法确定
二、判断题(共5小题,每小题2分,满分10分)
8.上、下两个底面相等的物体一定是圆柱。( )
9.求圆柱形容器的容积,就是求这个容器里面能容纳的物体的体积。( )
10.将圆锥沿高切开,所得到的横截面是一个等腰三角形。( )
11.一个圆柱的体积是一个圆锥的倍,那么它们等底等高。( )
12.圆柱的体积一般比它的表面积大。( )
三、填空题(共8小题,每小题2分,满分16分)
13.一个圆柱的底面周长是分米,高是分米,它的侧面积是( )平方分米,体积是( )立方分米。
14.一个透明的圆柱形水杯,从正面看如图所示,杯中已装有的水,还可以装()的水。
15.一个直角三角形的两条直角边分别是和,以其中一条直角边为轴旋转一周后所形成的立体图形是( ),它的体积最大是( )。
16.一个圆柱形水桶的容积是升,从里面量,水桶的底面积是平方分米,现在装了桶水,那么水面的高度是( )分米。
17.把一个长、宽、高的长方体木块削成一个最大的圆柱,圆柱的体积是()。
18.一个圆柱高,如果它的高减少,侧面积就减少。原来这个圆柱的体积是( )。
19.一个圆柱的体积是立方分米,当它的底面半径扩大为原来的倍,高变为原来的时,体积变成( )立方分米。
20.把一个圆柱削成一个最大的圆锥后,削去部分体积比这个圆锥体积大,原来圆柱的体积是( ),这个圆锥的体积是( )。
四、计算题(共3小题,每小题8分,满分24分)
21.求下列圆柱的侧面积。
(1)底面半径是,高是。
(2)底面积是,高是。
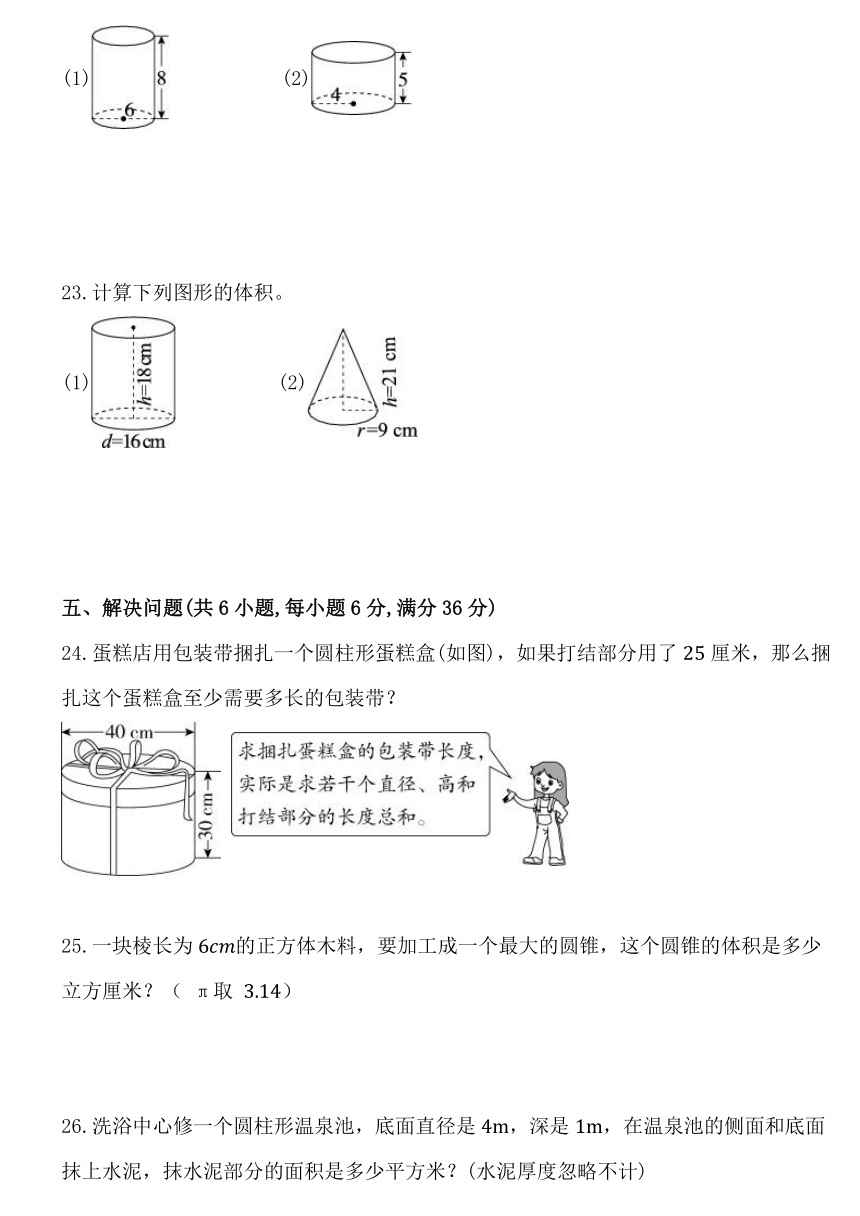
22.计算下面圆柱的表面积。(单位:)
(1) (2)
23.计算下列图形的体积。
(1) (2)
五、解决问题(共6小题,每小题6分,满分36分)
24.蛋糕店用包装带捆扎一个圆柱形蛋糕盒(如图),如果打结部分用了厘米,那么捆扎这个蛋糕盒至少需要多长的包装带?
25.一块棱长为的正方体木料,要加工成一个最大的圆锥,这个圆锥的体积是多少立方厘米?( 取 )
26.洗浴中心修一个圆柱形温泉池,底面直径是,深是,在温泉池的侧面和底面抹上水泥,抹水泥部分的面积是多少平方米?(水泥厚度忽略不计)
27.一个圆锥形的沙堆,它的占地面积是,高是,每立方米沙子重。用一辆载质量为的汽车把这堆沙子运走,至少要几次才能运完?
28.一个圆柱形容器,底面周长是厘米,高是厘米,把一个底面直径是厘米,高是厘米的圆锥形铁块放入圆柱形容器中并加水,使水正好淹没铁块,当把铁块取出后,容器中的水高多少厘米?
29.学校用的自来水水管的内直径为,自来水的流速一般为每秒,如果某一天忘记关上水龙头,一分钟将浪费多少升水
参考答案
1.A
2.C
3.B
4.D
5.D
6.D
7.C
8.错
9.对
10.对
11.错
12.错
13.;
14.
15.圆锥;
16.
17.
【解析】以长宽的面作底面,作高,削成的圆柱的体积最大。
18.
19.
20.;
【解析】把一个圆柱削成一个最大的圆锥,那么这个圆柱和圆锥等底等高,根据等底等高的圆柱体积是圆锥体积的倍,设这个圆锥的体积是,那么原来圆柱的体积是,根据削去部分体积比这个圆锥体积大,就是原来圆柱的体积圆锥体积圆锥体积,则原来圆柱的体积是,这个圆锥的体积是。
故答案为:,。
21.(1)
(2)假设圆柱的底面半径为。
22.(1)(平方厘米)
(2)(平方厘米)
23.(1)圆柱的体积:
(2)圆锥的体积:
24.(厘米)
【解析】包装带的长度等于个直径、条高和打结部分的长度和。
25.(立方厘米)
答:这个圆锥的体积是立方厘米。
26.
答:抹水泥部分的面积是。
27.(次)
答:至少要次才能运完。
28.(厘米)
答:容器中的水高厘米。
【解析】根据圆锥的体积公式,先求出圆锥形铁块的体积,即下降部分的水的体积,然后除以圆柱形容器的底面积,求出水面下降的高度,最后用原来水的高度减去下降的高度,就可以求出此时容器中水的高度。
29.分秒
答:一分钟将浪费水。
【解析】自来水水管的形状是圆柱形,要求一分钟浪费多少升水,就应根据圆柱的体积计算公式求出每秒流出的水量,然后乘秒。
一、选择题(共7小题,每小题2分,满分14分)
1.计算一个烟筒需要多少铁皮,是求它的( )。
A.侧面积 B.表面积 C.体积 D.溶积
2.下面四种测量圆锥高的方法中,( )是正确的。
A. B. C. D.
3.小明买了一瓶水,喝掉了一部分后还有剩余(如图所示),已知这个瓶子的内直径是。根据图中标出的数据,小明用算式“”计算的是( )。
A.喝掉的水的体积 B.瓶子的容积
C.剩余的水的体积 D.喝掉的水和剩余的水相差的体积
4.一根圆柱形木料的底面半径是,长是。如图所示,将它截成段,求这些木料的表面积比原来增加了多少平方米。列式是( )。
A. B. C. D.
5.一个圆柱形水桶,从里面量直径为,桶深。现将水倒进桶里,水占水桶容积的( )。
A. B. C. D.
6.如图,把一个圆柱切拼成一个近似的长方体,比较切拼前、后的体积和表面积,下面说法正确的是( )。
A.体积、表面积均不变 B.体积变小,表面积不变
C.体积不变,表面积变小 D.体积不变,表面积变大
7.如图,这两个等底等高的容器内的沙子图中阴影部分相比,( )。
A.甲比乙多 B.乙比甲多 C.同样多 D.无法确定
二、判断题(共5小题,每小题2分,满分10分)
8.上、下两个底面相等的物体一定是圆柱。( )
9.求圆柱形容器的容积,就是求这个容器里面能容纳的物体的体积。( )
10.将圆锥沿高切开,所得到的横截面是一个等腰三角形。( )
11.一个圆柱的体积是一个圆锥的倍,那么它们等底等高。( )
12.圆柱的体积一般比它的表面积大。( )
三、填空题(共8小题,每小题2分,满分16分)
13.一个圆柱的底面周长是分米,高是分米,它的侧面积是( )平方分米,体积是( )立方分米。
14.一个透明的圆柱形水杯,从正面看如图所示,杯中已装有的水,还可以装()的水。
15.一个直角三角形的两条直角边分别是和,以其中一条直角边为轴旋转一周后所形成的立体图形是( ),它的体积最大是( )。
16.一个圆柱形水桶的容积是升,从里面量,水桶的底面积是平方分米,现在装了桶水,那么水面的高度是( )分米。
17.把一个长、宽、高的长方体木块削成一个最大的圆柱,圆柱的体积是()。
18.一个圆柱高,如果它的高减少,侧面积就减少。原来这个圆柱的体积是( )。
19.一个圆柱的体积是立方分米,当它的底面半径扩大为原来的倍,高变为原来的时,体积变成( )立方分米。
20.把一个圆柱削成一个最大的圆锥后,削去部分体积比这个圆锥体积大,原来圆柱的体积是( ),这个圆锥的体积是( )。
四、计算题(共3小题,每小题8分,满分24分)
21.求下列圆柱的侧面积。
(1)底面半径是,高是。
(2)底面积是,高是。
22.计算下面圆柱的表面积。(单位:)
(1) (2)
23.计算下列图形的体积。
(1) (2)
五、解决问题(共6小题,每小题6分,满分36分)
24.蛋糕店用包装带捆扎一个圆柱形蛋糕盒(如图),如果打结部分用了厘米,那么捆扎这个蛋糕盒至少需要多长的包装带?
25.一块棱长为的正方体木料,要加工成一个最大的圆锥,这个圆锥的体积是多少立方厘米?( 取 )
26.洗浴中心修一个圆柱形温泉池,底面直径是,深是,在温泉池的侧面和底面抹上水泥,抹水泥部分的面积是多少平方米?(水泥厚度忽略不计)
27.一个圆锥形的沙堆,它的占地面积是,高是,每立方米沙子重。用一辆载质量为的汽车把这堆沙子运走,至少要几次才能运完?
28.一个圆柱形容器,底面周长是厘米,高是厘米,把一个底面直径是厘米,高是厘米的圆锥形铁块放入圆柱形容器中并加水,使水正好淹没铁块,当把铁块取出后,容器中的水高多少厘米?
29.学校用的自来水水管的内直径为,自来水的流速一般为每秒,如果某一天忘记关上水龙头,一分钟将浪费多少升水
参考答案
1.A
2.C
3.B
4.D
5.D
6.D
7.C
8.错
9.对
10.对
11.错
12.错
13.;
14.
15.圆锥;
16.
17.
【解析】以长宽的面作底面,作高,削成的圆柱的体积最大。
18.
19.
20.;
【解析】把一个圆柱削成一个最大的圆锥,那么这个圆柱和圆锥等底等高,根据等底等高的圆柱体积是圆锥体积的倍,设这个圆锥的体积是,那么原来圆柱的体积是,根据削去部分体积比这个圆锥体积大,就是原来圆柱的体积圆锥体积圆锥体积,则原来圆柱的体积是,这个圆锥的体积是。
故答案为:,。
21.(1)
(2)假设圆柱的底面半径为。
22.(1)(平方厘米)
(2)(平方厘米)
23.(1)圆柱的体积:
(2)圆锥的体积:
24.(厘米)
【解析】包装带的长度等于个直径、条高和打结部分的长度和。
25.(立方厘米)
答:这个圆锥的体积是立方厘米。
26.
答:抹水泥部分的面积是。
27.(次)
答:至少要次才能运完。
28.(厘米)
答:容器中的水高厘米。
【解析】根据圆锥的体积公式,先求出圆锥形铁块的体积,即下降部分的水的体积,然后除以圆柱形容器的底面积,求出水面下降的高度,最后用原来水的高度减去下降的高度,就可以求出此时容器中水的高度。
29.分秒
答:一分钟将浪费水。
【解析】自来水水管的形状是圆柱形,要求一分钟浪费多少升水,就应根据圆柱的体积计算公式求出每秒流出的水量,然后乘秒。
