3.1.1图形的平移(第1课时) 课件(共40张PPT)
文档属性
| 名称 | 3.1.1图形的平移(第1课时) 课件(共40张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-31 00:00:00 | ||
图片预览





文档简介
(共40张PPT)
北师大八下数学
同步精品课件
北师大版八年级下册
第三章 图形的平移与旋转
第1课时
平移的认识及性质
3.1 图形的平移
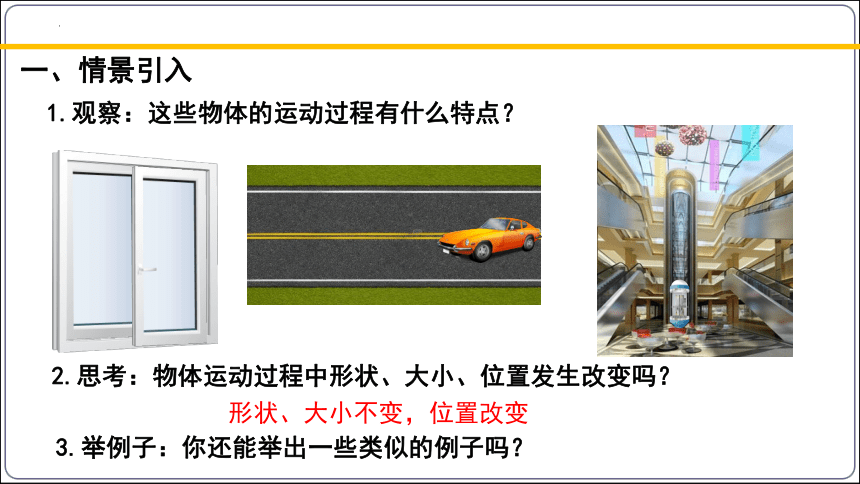
1.观察:这些物体的运动过程有什么特点?
一、情景引入
2.思考:物体运动过程中形状、大小、位置发生改变吗?
形状、大小不变,位置改变
3.举例子:你还能举出一些类似的例子吗?
思考:尝试总结以上运动过程具备什么共同特征?
8米
4米
问题:请你用一句话描述下面运动.
二、探索新知
国旗向上移动15米
行李向左移动8米
物品向右上方移动4米
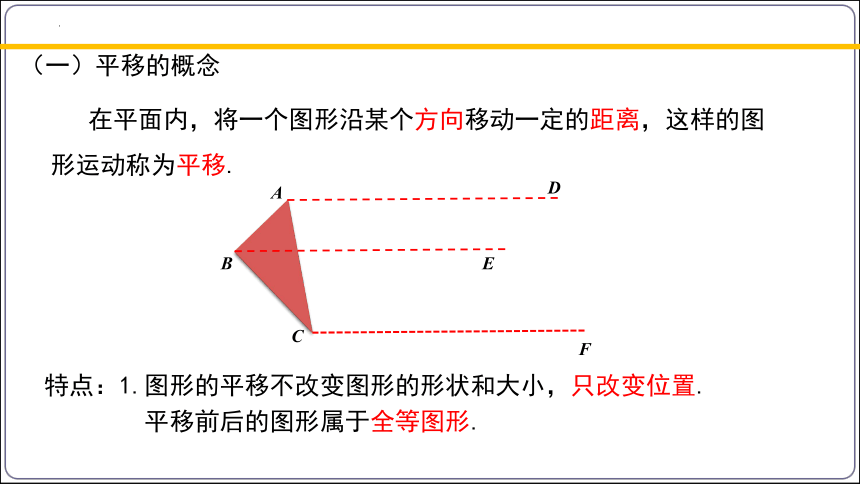
特点:1.图形的平移不改变图形的形状和大小,只改变位置.
平移前后的图形属于全等图形.
A
B
C
D
E
F
在平面内,将一个图形沿某个方向移动一定的距离,这样的图形运动称为平移.
(一)平移的概念
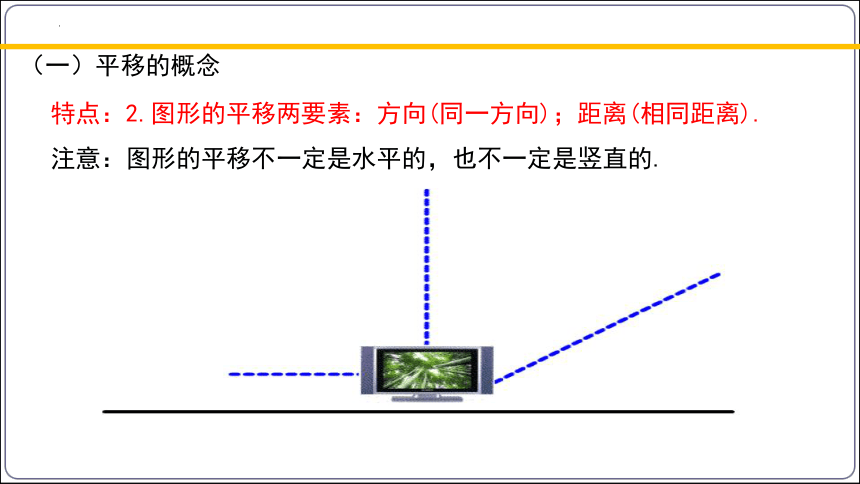
注意:图形的平移不一定是水平的,也不一定是竖直的.
(一)平移的概念
特点:2.图形的平移两要素:方向(同一方向);距离(相同距离).
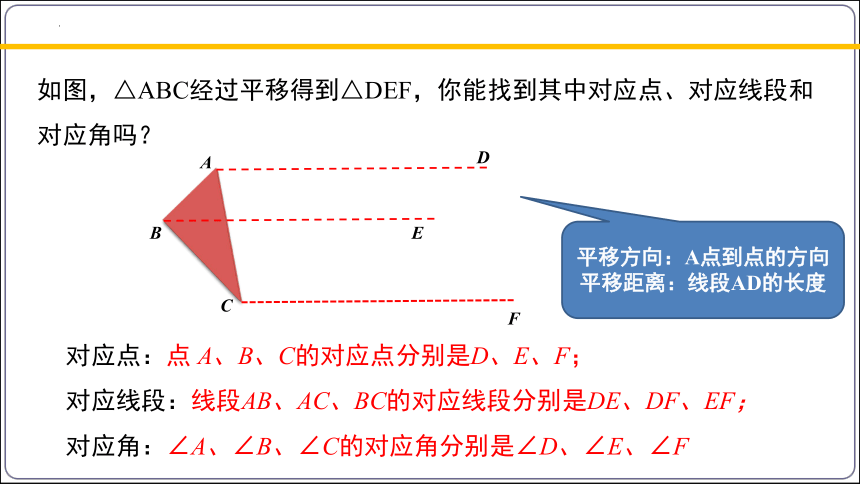
如图,△ABC经过平移得到△DEF,你能找到其中对应点、对应线段和对应角吗?
对应点:点 A、B、C的对应点分别是D、E、F;
对应线段:线段AB、AC、BC的对应线段分别是DE、DF、EF;
对应角:∠A、∠B、∠C的对应角分别是∠D、∠E、∠F
A
B
C
D
E
F
平移方向:A点到点的方向
平移距离:线段AD的长度
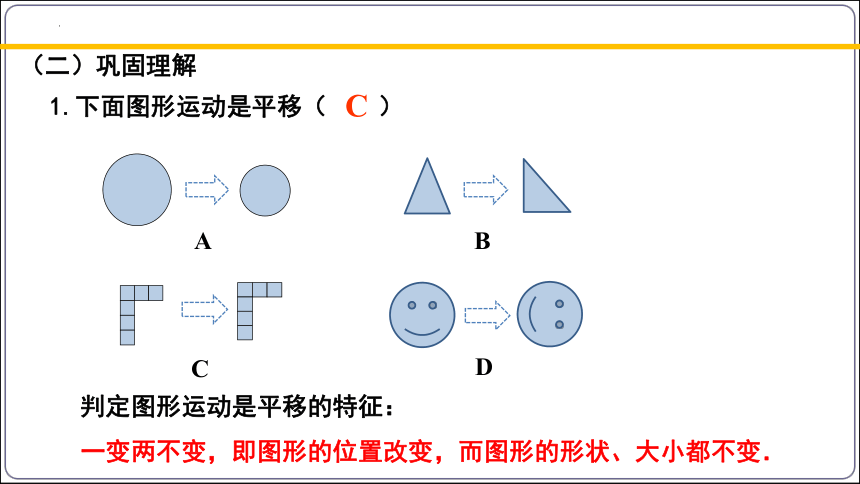
判定图形运动是平移的特征:
一变两不变,即图形的位置改变,而图形的形状、大小都不变.
1.下面图形运动是平移( )
A
C
D
B
C
(二)巩固理解
2.以下现象,其中属于平移的是( )
①打开教室的门时,门的移动;
②打气筒打气时,活塞的运动;
③钟摆的摆动;
④传送带上,瓶装饮料的移动
A.①② B.①③
C.②③ D.②④
D
(二)巩固理解
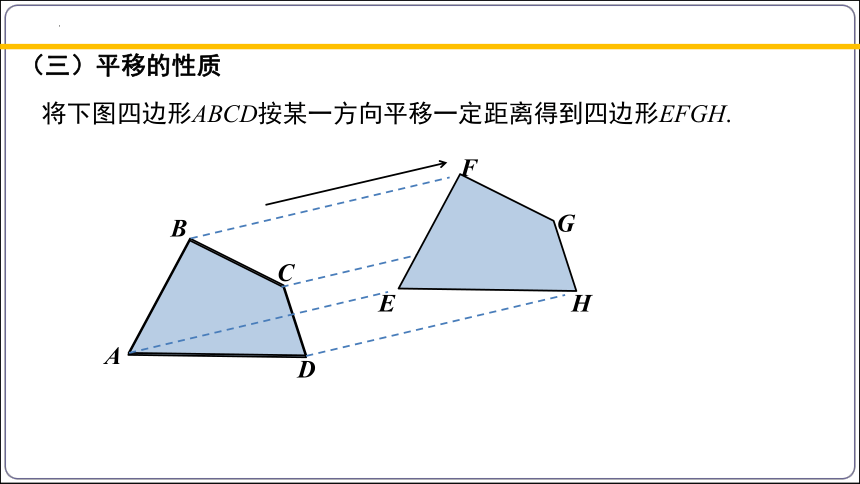
将下图四边形ABCD按某一方向平移一定距离得到四边形EFGH.
A
B
C
D
E
F
G
H
(三)平移的性质
A
B
C
D
E
F
G
H
(1)在图中任选一组对应线段,每对对应线段有怎样的关系?
包括数量关系与位置关系
∴AB∥EF,BC∥FG,CD∥GH ,AD∥EH
AB=EF,BC=FG,CD=GH ,AD=EH
A
B
C
D
E
F
G
H
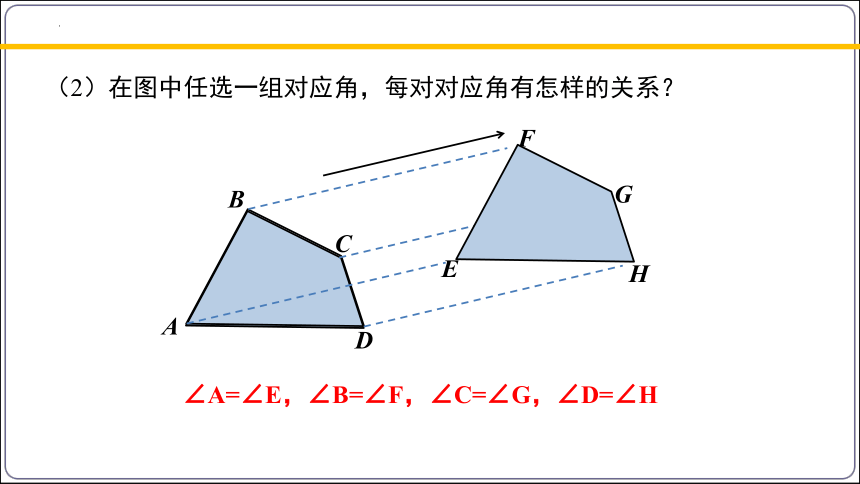
(2)在图中任选一组对应角,每对对应角有怎样的关系?
∠A=∠E,∠B=∠F,∠C=∠G,∠D=∠H
A
B
C
D
E
F
G
H
(3)对应点所连接的线段,它们之间有什么关系?
线段AE,BF,CG,DH
AE∥BF∥CG∥DH
AE=BF=CG=DH
改变图形的形状,上述性质还成立吗?
性质 几何语言 图示
对应线段平行(或在同一直线上)且相等
∵△ABC平移得到△DEF,
∴AB∥DE,AC∥DF,BC∥EF(或共线)
AB=DE,AC=DF,BC=EF.
对应角相等
对应点所连的线段平行(或在同一直线上)且相等
∵△ABC平移得到△DEF,
∴∠BAC=∠EDF, ∠ABC=∠DEF,∠ACB=∠DFE
∵△ABC平移得到△DEF,
∴AD∥BE∥CF(或共线),
AD=BE=CF
A
B
C
D
E
F
A
B
C
D
E
F
图形平移的基本性质:
方法总结
平移性质理解的两个角度
(1)位置:对应线段平行或在同一条直线上;对应点的连线平行或在同一条直线上.
(2)数量:对应线段相等;对应角相等;对应点的连线相等.
A
B
C
D
E
F
A
B
C
D
E
F
3.经过平移,△ABC的顶点A移到了点D.
(1)指出平移的方向和平移的距离;
(2)画出平移后的三角形.
A
B
C
D
(三)巩固练习
解:(1)如图,连接AD ,平移的方向是点A到点D的方向,平移的距离是线段AD的长度.
(2)如图,分别过点B,C按射线AD的方向作线段BE,CF,使得它们与线段AD平行且相等,连接DE,DF,EF, △DEF就是△ABC平移后的图形.
A
B
C
D
E
F
你还有画△DEF的其他方法呢?
A
B
C
D
解:如图,过点D按射线AB的方向做线段DE平行且等于AB;过点D按射线AC的方向做线段DF平行且等于AC;连接EF. ΔDEF 就是ΔABC平移后的图形.
A
B
C
D
A
B
C
D
E
F
平移作图的一般步骤:
应分四步——定、找、移、连.
(1)定:确定平移的方向和距离;
(2)找:找出表示图形的关键点(图形的顶点、拐点、连接点);
(3)移:过关键点作平行且相等的线段,得到关键点的对应点;
(平行和相等可以按照平移方向和距离,也可以按照对应边的关系)
(4)连:按原图顺次连接对应点.
例1:冰墩墩,是2022年北京冬季奥运会的吉祥物.冰墩墩寓意创造非凡、探索未来,体现了追求卓越、引领时代,以及面向未来的无限可能.下面哪个图形是由冰墩墩平移得到( )
三、典例精练
知识点一:平移的概念
A. B. C. D.
D
例2.如图,△ABC以每秒2cm的速度沿着射线BC向右平移,平移2秒后所得图形是△DEF,如果AD=2CE,那么BC的长是( )
A.4
B.6
C.8
D.9
三、典例精练
知识点二:平移的性质
B
例3.如图,将△ABC平移到△A′B′C′的位置,使点B′在AC边上,若∠B=55°,∠C=100°,则∠AB′A′的度数为______.
25°
三、典例精练
知识点二:平移的性质
三、典例精练
知识点二:平移的性质
例4.如图,将直角三角形ABC沿BC方向平移得到直角三角DEF.若AB=8cm,BE=4cm,DH=2cm,则图中阴影部分面积为( )
A
A.28cm2
B.29cm2
C.30cm2
D.32cm2
例5:将图中的字母N沿水平方向向右平移3cm,作出平移后的图形.
三、典例精练
知识点三:平移的画图
平移作图的步骤:(1)定方向;(2)定距离;(3)找对应点;(4)连线段
1.下面生活现象中,物体的运动情况可以看成平移的是( )A.时钟摆动的钟摆 B.在笔直的公路上行驶的汽车 C.体温计中水银柱的上升 D.汽车玻璃窗上雨刷的运动
四、课堂练习
B
2. 在图形平移中,下面说法中错误的是( )
A. 图形上任意点移动的方向相同
B. 图形上任意点移动的距离相等
C. 图形上任意两点的连线的长度不变
D. 图形上可能存在不动点
D
四、课堂练习
3.如图,△ABC经过平移得到△DEF,其中点A的对应点是点D,则下列结论不一定正确的是 ( )
A.BC∥EF
B.AD=BE
C.BE∥CF
D.AC=EF
D
四、课堂练习
4. 如图,△ABC沿着由点B到点E的方向平移到△DEF,已知BC=5,EC=3,那么平移的距离为 ( )
A.2
B.3
C.5
D.7
A
四、课堂练习
5.如图,将△ABE向右平移2 cm得到△DCF,△ABE的周长是16cm,那么四边形ABFD的周长是 ( )
A.16 cm
B.18 cm
C.20 cm
D.21 cm
C
四、课堂练习
6. 如图,将△ABC沿射线AB的方向平移到△DEF的位置,点A、B、C的对应点分别为点D、E、F,若∠ABC=75°,则∠CFE= °.
105
四、课堂练习
7.如图,图中小正方形的边长为a,则阴影部分的面积是____
a2
四、课堂练习
8. 如图,经过平移,△ABC的边AB移到了EF,画出平移后的三角形.
解:如图,△EFD为平移后的三角形.
四、课堂练习
1m
1m
21m
15m
A
C
D
B
图 1
9.如图是一块长方形的草地,长为21米.宽为15米 在草地上有两条宽为1米的小道,长方形的草地上除小道外长满青草,求长草部分的面积为多少
1m
1m
21m
15m
A
C
D
B
图 1
四、课堂练习
解:S草地=(21-1)×(15-1)=20×14=280(m2).
答:草地面积为540平方米.
1m
21m
15m
A
C
D
B
变式:如图是一块长方形的草地, 长为21米.宽为15米.在草地上有一条宽为1米的小道,长方形的草地上除小道外长满青草.求长草部分的面积为多少
解:S草地=(21-1)×(15-1)=20×14=280(m2).
答:草地面积为540平方米.
四、课堂练习
10.如图,△ABC是边长为2的等边三角形,将△ABC沿直线BC平移到△DCE的位置,连接BD.
(1)△ABC平移的距离为________;
(2)求BD的长.
四、课堂练习
2
解(2)∵BE=2BC=4,DE=AC=2,
∠E=∠ACB=60°,
又∵∠E=∠ACB=60°,
∴AC∥DE,∴BD⊥AC,
∴△BED是直角三角形,
∵BE=4,DE=2,
∴DE= BE,∴BD⊥DE,
∴BD= = .
五、课堂小结
平移 内容 图示
定义
在平面内,将一个图形沿某个方向移动一定的距离,这样的图形运动称为平移.
特征
1.平移不改变图形的形状和大小,只改变位置.
2.平移前后的图形属于全等图形;
3.两要素:方向与距离
A
B
C
D
E
F
作图
(1)定:确定方向和距离;(2)找:找图形的关键点;
(3)移:平移得到关键点的对应点;
(4)连:按原图顺次连接对应点.
性质 几何语言 图示
对应线段平行(或在同一直线上)且相等
∵△ABC平移得到△DEF,
∴AB∥DE,AC∥DF,BC∥EF(或共线)
AB=DE,AC=DF,BC=EF.
对应角相等
对应点所连的线段平行(或在同一直线上)且相等
∵△ABC平移得到△DEF,
∴∠BAC=∠EDF, ∠ABC=∠DEF,∠ACB=∠DFE
∵△ABC平移得到△DEF,
∴AD∥BE∥CF(或共线),
AD=BE=CF
A
B
C
D
E
F
A
B
C
D
E
F
图形平移的基本性质:
完成课本P67第1、2、3、4、5题
六、布置作业
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
北师大八下数学
同步精品课件
北师大版八年级下册
第三章 图形的平移与旋转
第1课时
平移的认识及性质
3.1 图形的平移
1.观察:这些物体的运动过程有什么特点?
一、情景引入
2.思考:物体运动过程中形状、大小、位置发生改变吗?
形状、大小不变,位置改变
3.举例子:你还能举出一些类似的例子吗?
思考:尝试总结以上运动过程具备什么共同特征?
8米
4米
问题:请你用一句话描述下面运动.
二、探索新知
国旗向上移动15米
行李向左移动8米
物品向右上方移动4米
特点:1.图形的平移不改变图形的形状和大小,只改变位置.
平移前后的图形属于全等图形.
A
B
C
D
E
F
在平面内,将一个图形沿某个方向移动一定的距离,这样的图形运动称为平移.
(一)平移的概念
注意:图形的平移不一定是水平的,也不一定是竖直的.
(一)平移的概念
特点:2.图形的平移两要素:方向(同一方向);距离(相同距离).
如图,△ABC经过平移得到△DEF,你能找到其中对应点、对应线段和对应角吗?
对应点:点 A、B、C的对应点分别是D、E、F;
对应线段:线段AB、AC、BC的对应线段分别是DE、DF、EF;
对应角:∠A、∠B、∠C的对应角分别是∠D、∠E、∠F
A
B
C
D
E
F
平移方向:A点到点的方向
平移距离:线段AD的长度
判定图形运动是平移的特征:
一变两不变,即图形的位置改变,而图形的形状、大小都不变.
1.下面图形运动是平移( )
A
C
D
B
C
(二)巩固理解
2.以下现象,其中属于平移的是( )
①打开教室的门时,门的移动;
②打气筒打气时,活塞的运动;
③钟摆的摆动;
④传送带上,瓶装饮料的移动
A.①② B.①③
C.②③ D.②④
D
(二)巩固理解
将下图四边形ABCD按某一方向平移一定距离得到四边形EFGH.
A
B
C
D
E
F
G
H
(三)平移的性质
A
B
C
D
E
F
G
H
(1)在图中任选一组对应线段,每对对应线段有怎样的关系?
包括数量关系与位置关系
∴AB∥EF,BC∥FG,CD∥GH ,AD∥EH
AB=EF,BC=FG,CD=GH ,AD=EH
A
B
C
D
E
F
G
H
(2)在图中任选一组对应角,每对对应角有怎样的关系?
∠A=∠E,∠B=∠F,∠C=∠G,∠D=∠H
A
B
C
D
E
F
G
H
(3)对应点所连接的线段,它们之间有什么关系?
线段AE,BF,CG,DH
AE∥BF∥CG∥DH
AE=BF=CG=DH
改变图形的形状,上述性质还成立吗?
性质 几何语言 图示
对应线段平行(或在同一直线上)且相等
∵△ABC平移得到△DEF,
∴AB∥DE,AC∥DF,BC∥EF(或共线)
AB=DE,AC=DF,BC=EF.
对应角相等
对应点所连的线段平行(或在同一直线上)且相等
∵△ABC平移得到△DEF,
∴∠BAC=∠EDF, ∠ABC=∠DEF,∠ACB=∠DFE
∵△ABC平移得到△DEF,
∴AD∥BE∥CF(或共线),
AD=BE=CF
A
B
C
D
E
F
A
B
C
D
E
F
图形平移的基本性质:
方法总结
平移性质理解的两个角度
(1)位置:对应线段平行或在同一条直线上;对应点的连线平行或在同一条直线上.
(2)数量:对应线段相等;对应角相等;对应点的连线相等.
A
B
C
D
E
F
A
B
C
D
E
F
3.经过平移,△ABC的顶点A移到了点D.
(1)指出平移的方向和平移的距离;
(2)画出平移后的三角形.
A
B
C
D
(三)巩固练习
解:(1)如图,连接AD ,平移的方向是点A到点D的方向,平移的距离是线段AD的长度.
(2)如图,分别过点B,C按射线AD的方向作线段BE,CF,使得它们与线段AD平行且相等,连接DE,DF,EF, △DEF就是△ABC平移后的图形.
A
B
C
D
E
F
你还有画△DEF的其他方法呢?
A
B
C
D
解:如图,过点D按射线AB的方向做线段DE平行且等于AB;过点D按射线AC的方向做线段DF平行且等于AC;连接EF. ΔDEF 就是ΔABC平移后的图形.
A
B
C
D
A
B
C
D
E
F
平移作图的一般步骤:
应分四步——定、找、移、连.
(1)定:确定平移的方向和距离;
(2)找:找出表示图形的关键点(图形的顶点、拐点、连接点);
(3)移:过关键点作平行且相等的线段,得到关键点的对应点;
(平行和相等可以按照平移方向和距离,也可以按照对应边的关系)
(4)连:按原图顺次连接对应点.
例1:冰墩墩,是2022年北京冬季奥运会的吉祥物.冰墩墩寓意创造非凡、探索未来,体现了追求卓越、引领时代,以及面向未来的无限可能.下面哪个图形是由冰墩墩平移得到( )
三、典例精练
知识点一:平移的概念
A. B. C. D.
D
例2.如图,△ABC以每秒2cm的速度沿着射线BC向右平移,平移2秒后所得图形是△DEF,如果AD=2CE,那么BC的长是( )
A.4
B.6
C.8
D.9
三、典例精练
知识点二:平移的性质
B
例3.如图,将△ABC平移到△A′B′C′的位置,使点B′在AC边上,若∠B=55°,∠C=100°,则∠AB′A′的度数为______.
25°
三、典例精练
知识点二:平移的性质
三、典例精练
知识点二:平移的性质
例4.如图,将直角三角形ABC沿BC方向平移得到直角三角DEF.若AB=8cm,BE=4cm,DH=2cm,则图中阴影部分面积为( )
A
A.28cm2
B.29cm2
C.30cm2
D.32cm2
例5:将图中的字母N沿水平方向向右平移3cm,作出平移后的图形.
三、典例精练
知识点三:平移的画图
平移作图的步骤:(1)定方向;(2)定距离;(3)找对应点;(4)连线段
1.下面生活现象中,物体的运动情况可以看成平移的是( )A.时钟摆动的钟摆 B.在笔直的公路上行驶的汽车 C.体温计中水银柱的上升 D.汽车玻璃窗上雨刷的运动
四、课堂练习
B
2. 在图形平移中,下面说法中错误的是( )
A. 图形上任意点移动的方向相同
B. 图形上任意点移动的距离相等
C. 图形上任意两点的连线的长度不变
D. 图形上可能存在不动点
D
四、课堂练习
3.如图,△ABC经过平移得到△DEF,其中点A的对应点是点D,则下列结论不一定正确的是 ( )
A.BC∥EF
B.AD=BE
C.BE∥CF
D.AC=EF
D
四、课堂练习
4. 如图,△ABC沿着由点B到点E的方向平移到△DEF,已知BC=5,EC=3,那么平移的距离为 ( )
A.2
B.3
C.5
D.7
A
四、课堂练习
5.如图,将△ABE向右平移2 cm得到△DCF,△ABE的周长是16cm,那么四边形ABFD的周长是 ( )
A.16 cm
B.18 cm
C.20 cm
D.21 cm
C
四、课堂练习
6. 如图,将△ABC沿射线AB的方向平移到△DEF的位置,点A、B、C的对应点分别为点D、E、F,若∠ABC=75°,则∠CFE= °.
105
四、课堂练习
7.如图,图中小正方形的边长为a,则阴影部分的面积是____
a2
四、课堂练习
8. 如图,经过平移,△ABC的边AB移到了EF,画出平移后的三角形.
解:如图,△EFD为平移后的三角形.
四、课堂练习
1m
1m
21m
15m
A
C
D
B
图 1
9.如图是一块长方形的草地,长为21米.宽为15米 在草地上有两条宽为1米的小道,长方形的草地上除小道外长满青草,求长草部分的面积为多少
1m
1m
21m
15m
A
C
D
B
图 1
四、课堂练习
解:S草地=(21-1)×(15-1)=20×14=280(m2).
答:草地面积为540平方米.
1m
21m
15m
A
C
D
B
变式:如图是一块长方形的草地, 长为21米.宽为15米.在草地上有一条宽为1米的小道,长方形的草地上除小道外长满青草.求长草部分的面积为多少
解:S草地=(21-1)×(15-1)=20×14=280(m2).
答:草地面积为540平方米.
四、课堂练习
10.如图,△ABC是边长为2的等边三角形,将△ABC沿直线BC平移到△DCE的位置,连接BD.
(1)△ABC平移的距离为________;
(2)求BD的长.
四、课堂练习
2
解(2)∵BE=2BC=4,DE=AC=2,
∠E=∠ACB=60°,
又∵∠E=∠ACB=60°,
∴AC∥DE,∴BD⊥AC,
∴△BED是直角三角形,
∵BE=4,DE=2,
∴DE= BE,∴BD⊥DE,
∴BD= = .
五、课堂小结
平移 内容 图示
定义
在平面内,将一个图形沿某个方向移动一定的距离,这样的图形运动称为平移.
特征
1.平移不改变图形的形状和大小,只改变位置.
2.平移前后的图形属于全等图形;
3.两要素:方向与距离
A
B
C
D
E
F
作图
(1)定:确定方向和距离;(2)找:找图形的关键点;
(3)移:平移得到关键点的对应点;
(4)连:按原图顺次连接对应点.
性质 几何语言 图示
对应线段平行(或在同一直线上)且相等
∵△ABC平移得到△DEF,
∴AB∥DE,AC∥DF,BC∥EF(或共线)
AB=DE,AC=DF,BC=EF.
对应角相等
对应点所连的线段平行(或在同一直线上)且相等
∵△ABC平移得到△DEF,
∴∠BAC=∠EDF, ∠ABC=∠DEF,∠ACB=∠DFE
∵△ABC平移得到△DEF,
∴AD∥BE∥CF(或共线),
AD=BE=CF
A
B
C
D
E
F
A
B
C
D
E
F
图形平移的基本性质:
完成课本P67第1、2、3、4、5题
六、布置作业
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
