2024年九年级中考数学二轮专题复习课件 专题七 图形的折叠、旋转与平移 课件(共37张PPT)
文档属性
| 名称 | 2024年九年级中考数学二轮专题复习课件 专题七 图形的折叠、旋转与平移 课件(共37张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-31 12:28:56 | ||
图片预览



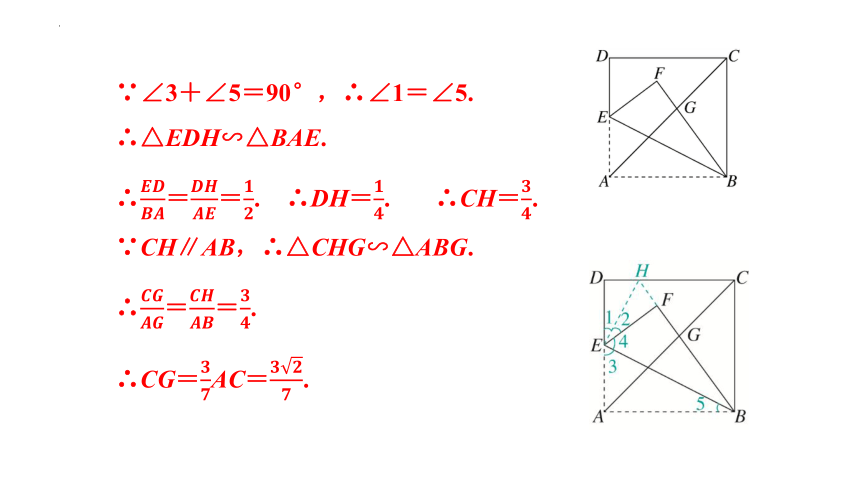
文档简介
(共37张PPT)
第二部分 专题复习
专题七 图形的折叠、旋转与平移
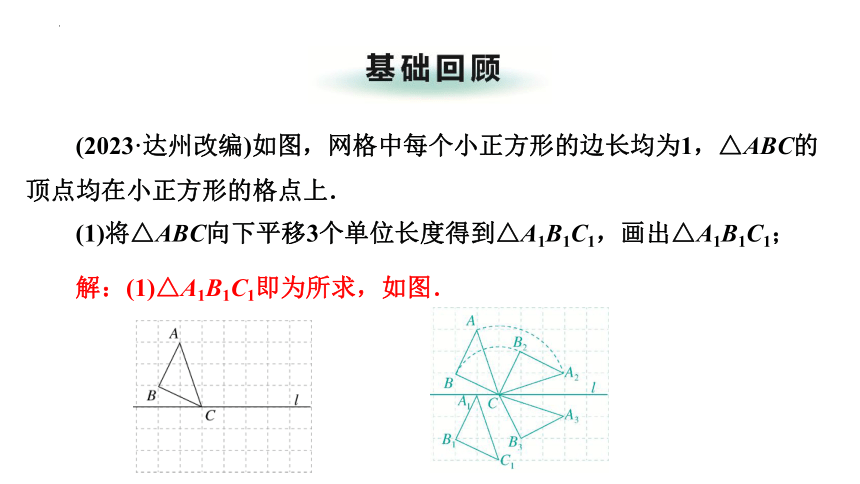
(2023·达州改编)如图,网格中每个小正方形的边长均为1,△ABC的顶点均在小正方形的格点上.
(1)将△ABC向下平移3个单位长度得到△A1B1C1,画出△A1B1C1;
解:(1)△A1B1C1即为所求,如图.
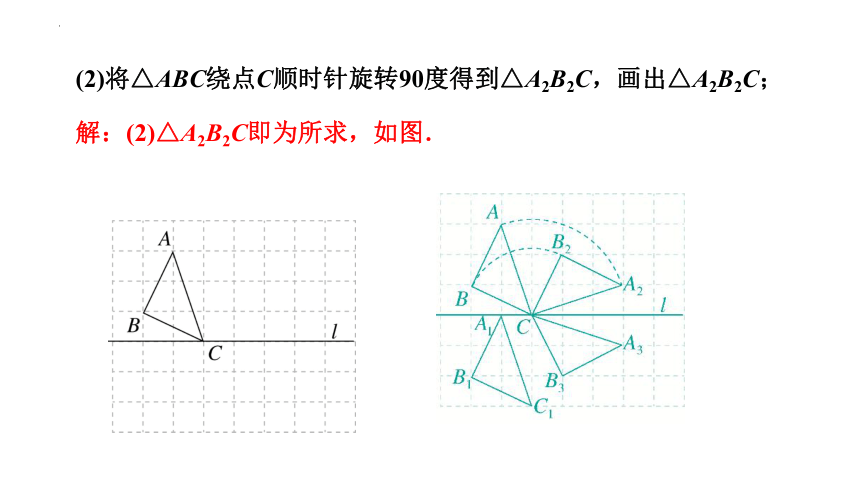
(2)将△ABC绕点C顺时针旋转90度得到△A2B2C,画出△A2B2C;
解:(2)△A2B2C即为所求,如图.
(3)在(2)的运动过程中请计算出△ABC扫过的面积;
(3)S△ABC=2×3-×2×1-×2×1-×3×1=.
∵AC==,∴S扇形AC ) ==.
∴在(2)的运动过程中△ABC扫过的面积为S=S△ABC+S扇形AC =.
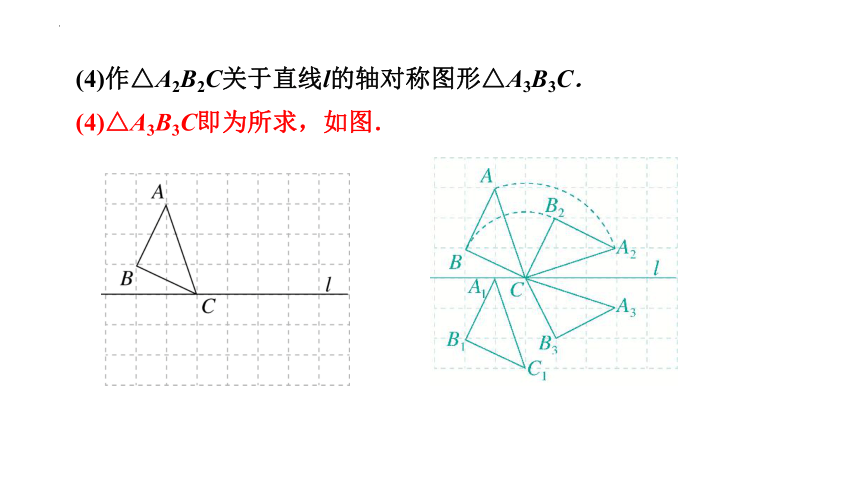
(4)作△A2B2C关于直线l的轴对称图形△A3B3C.
(4)△A3B3C即为所求,如图.
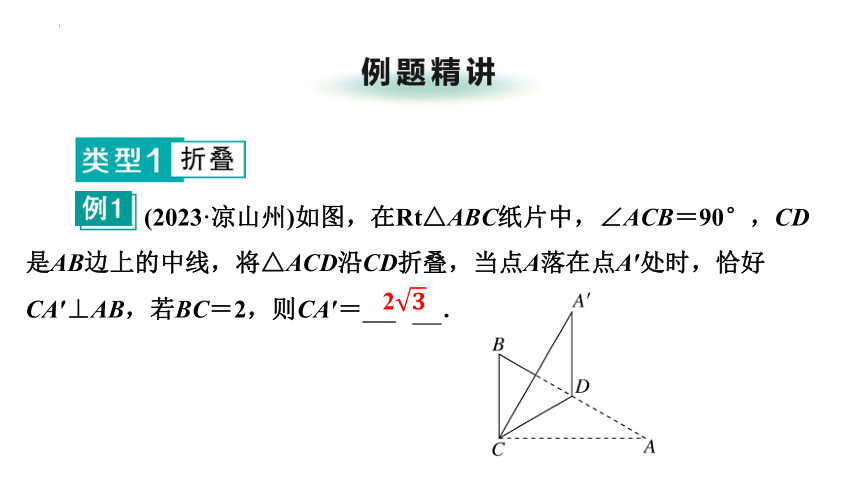
(2023·凉山州)如图,在Rt△ABC纸片中,∠ACB=90°,CD是AB边上的中线,将△ACD沿CD折叠,当点A落在点A′处时,恰好CA′⊥AB,若BC=2,则CA′= 2 .
2
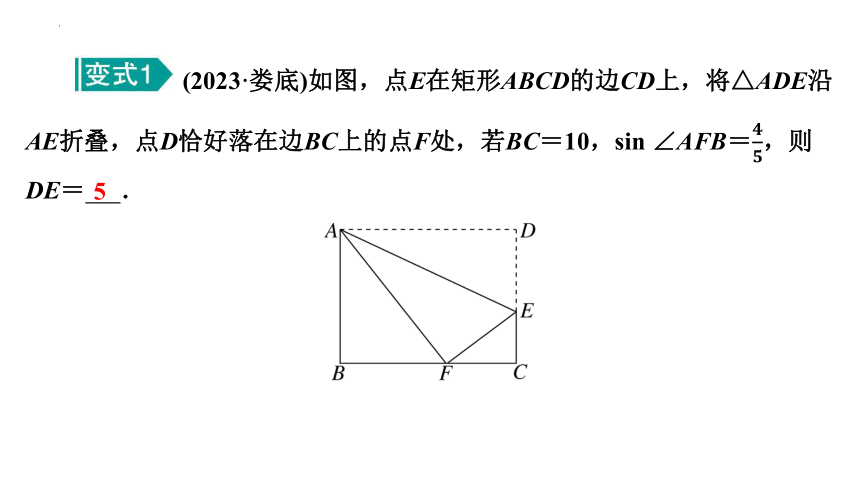
(2023·娄底)如图,点E在矩形ABCD的边CD上,将△ADE沿AE折叠,点D恰好落在边BC上的点F处,若BC=10,sin ∠AFB=,则DE= 5 .
5
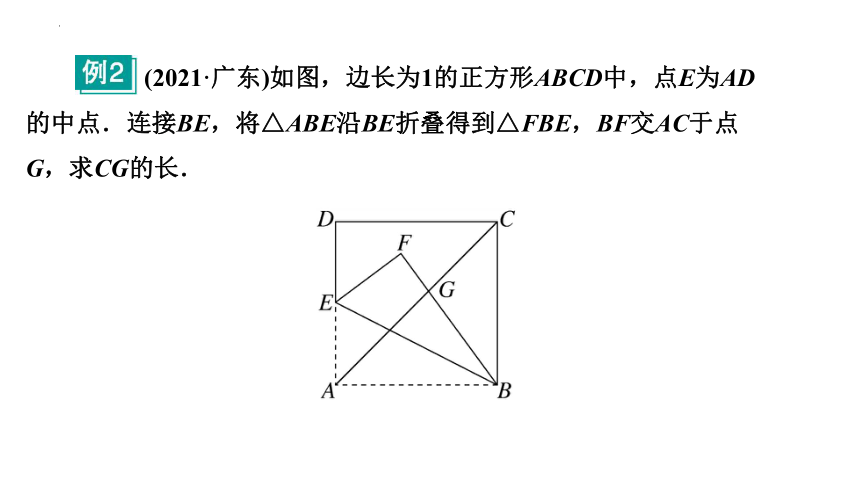
(2021·广东)如图,边长为1的正方形ABCD中,点E为AD的中点.连接BE,将△ABE沿BE折叠得到△FBE,BF交AC于点G,求CG的长.
解:如图,延长BF交CD于点H,连接EH.
∵四边形ABCD是正方形,
∴AB∥CD,∠D=∠DAB=90°,AD=CD=AB=1.
∴AC===.
由翻折的性质可知,AE=EF,∠EAB=∠EFB=90°,∠3=∠4.
∵点E是AD的中点,∴AE=DE=EF=.
在Rt△EHD和Rt△EHF中,
∴Rt△EHD≌Rt△EHF(HL).∴∠1=∠2.
∵∠DEF+∠AEF=180°,∴2∠1+2∠3=180°.
∴∠1+∠3=90°.
∵∠3+∠5=90°,∴∠1=∠5.
∴△EDH∽△BAE.
∴==. ∴DH=. ∴CH=.
∵CH∥AB,∴△CHG∽△ABG.
∴==.
∴CG=AC=.
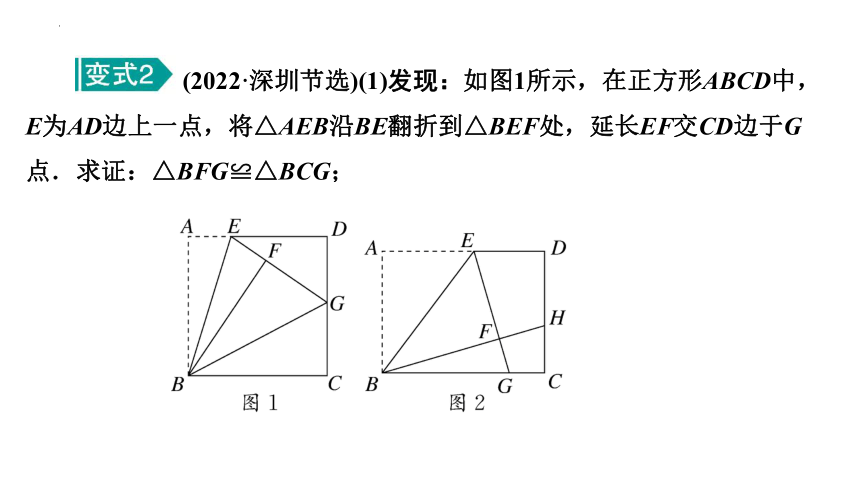
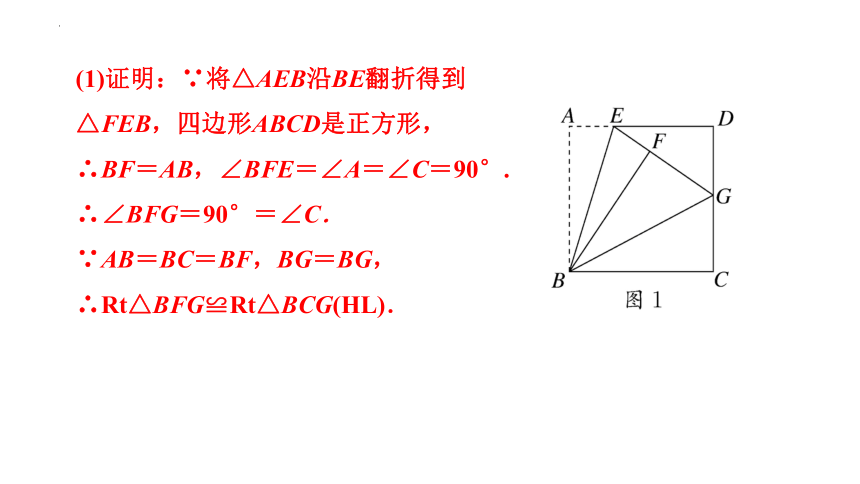
(2022·深圳节选)(1)发现:如图1所示,在正方形ABCD中,E为AD边上一点,将△AEB沿BE翻折到△BEF处,延长EF交CD边于G点.求证:△BFG≌△BCG;
(1)证明:∵将△AEB沿BE翻折得到
△FEB,四边形ABCD是正方形,
∴BF=AB,∠BFE=∠A=∠C=90°.
∴∠BFG=90°=∠C.
∵AB=BC=BF,BG=BG,
∴Rt△BFG≌Rt△BCG(HL).
(2)探究:如图2,在矩形ABCD中,E为AD边上一点,且AD=8,AB=6.将△AEB沿BE翻折到△BEF处,延长EF交BC边于点G,延长BF交CD边于点H,且FH=CH,求AE的长.
(2)解:延长BH,AD交于点Q,如图.
设FH=CH=x,则BH=6+x.
在Rt△BCH中,BC2+CH2=BH2,
即82+x2=(6+x)2.解得x=.
∴DH=DC-CH=.
∵∠BFG=∠BCH=90°,∠GBF=∠HBC,∴△BFG∽△BCH.
∴==,即==.
∴BG=,FG=.
∵DQ∥CB,∴△DHQ∽△CHB.
∴=,即=. ∴QD=.
设AE=EF=m,则DE=8-m.
∴EQ=DE+QD=8-m+=-m.
∵EQ∥GB,∴△EFQ∽△GFB.
∴=,即=.解得m=.
∴AE的长为.
(毕节中考)如图1,在Rt△ABC中,∠BAC=90°,AB=AC,D为△ABC内一点,将线段AD绕点A逆时针旋转90°得到AE,连接CE,BD的延长线与CE交于点F.
(1)求证:BD=CE,BD⊥CE;
(1)证明:如答图1,设AC与BF交于点O.
∵线段AD绕点A逆时针旋转90°得到AE,
∴AD=AE,∠DAE=90°.
∵∠BAC=90°,∴∠BAC=∠DAE.∴∠BAD=∠CAE.
在△ABD和△ACE中,
∴△ABD≌△ACE(SAS).∴BD=CE,∠ABD=∠ACE.
又∵∠AOB=∠COF,∴∠BFC=∠BAC=90°.∴BD⊥CE.
(2)如图2,连接AF,DC,已知∠BDC=135°,判断AF与DC的位置关系,并说明理由.
(2)解:AF∥DC.
理由如下:如答图2,过点A作AG⊥BF于点G,AH⊥CE于点H.
由(1)知△ABD≌△ACE.
∴BD=CE,S△ABD=S△ACE.
∴BD·AG=CE·AH. ∴AG=AH.
又∵AG⊥BF,AH⊥CE, ∴FA平分∠BFE.
又∵∠BFE=90°,∴∠AFD=45°.
∵∠BDC=135°,∴∠FDC=45°.
∴∠AFD=∠FDC.∴AF∥DC.
(2023·自贡)如图1,一大一小两个等腰直角三角形叠放在一起,M,N分别是斜边DE,AB的中点,DE=2,AB=4.
(1)将△CDE绕顶点C旋转一周,请直接写出点M,N距离的最大值和最小值;
解:(1)如答图1,以C为圆心,CM长为半径画圆,连接CN交DE于M1,延长NC交⊙C于M2.
∵△ACB是等腰直角三角形,N是AB的中点,
∴CN平分∠ACB,CN=AB=×4=2.
∵△DCE是等腰直角三角形,
∴M1是DE的中点.∴CM1=DE=×2=1.
∴点M,N距离的最小值是NM1=CN-CM1=2-1=1,点M,N距离的最大值是NM2=CN+CM2=2+1=3.
(2)将△CDE绕顶点C逆时针旋转120°(如图2),求MN的长.
(2)如答图2,连接CM,CN,作NH⊥MC交MC的延长线于点H.
∵△ACB是等腰直角三角形,点N是AB的中点,
∴CN=AB=2.同理,CM=DE=1.
∵△CDE绕顶点C逆时针旋转120°,∴∠MCN=120°.
∴∠NCH=180°-∠MCN=60°.
∴CH=CN=1.∴NH==.
∵MH=MC+CH=2,∴MN==.
(广东中考节选)如图,在平面直角坐标系中,抛物线y=x2+x-与x轴交于点A,B(点A在点B右侧),点D为抛物线的顶点,点C在y轴的正半轴上,CD交x轴于点F,△CAD绕点C顺时针旋转得到△CFE,点A恰好旋转到点F,连接BE.
(1)解:令x2+x-=0,解得x1=1,x2=-7.
∴A(1,0),B(-7,0).
由y=x2+x-=(x+3)2-2,得D(-3,-2).
(1)求点A,B,D的坐标;
(2)求证:四边形BFCE是平行四边形.
(2)证明:∵△CAD绕点C顺时针旋转得到△CFE,
∴∠ACF=∠ECF,CF=CA.
∵CO⊥AF,∴OF=OA=1.
∴F(-1,0).又D(-3,-2),
易求得直线DF的解析式为y=x+.
当x=0时,y=.
∴C(0,).
∴OC=.
∴CA=CF==2.
又FA=2,∴△ACF是等边三角形.
∴∠AFC=∠ACF.
∴∠ECF=∠ACF=∠AFC=60°.
∴EC∥BF.
∵EC=DC==6,BF=6,∴EC=BF.
∴四边形BFCE是平行四边形.
(2023·北京)在△ABC中,∠B=∠C=α(0°<α<45°),AM⊥BC于点M,D是线段MC上的动点(不与点M,C重合),将线段DM绕点D顺时针旋转2α得到线段DE.
(1)如图1,当点E在线段AC上时,求证:点D是MC的中点;
(1)证明:由旋转的性质,得DM=DE,∠MDE=2α.
∵∠C=α,∴∠DEC=∠MDE-∠C=α.
∴∠C=∠DEC.∴DE=DC.
∴DM=DC,即点D是MC的中点.
(2)如图2,若在线段BM上存在点F(不与点B,M重合)满足DF=DC,连接AE,EF,直接写出∠AEF的大小,并证明.
(2)解:∠AEF=90°.证明如下:
如图,延长FE到H使EH=FE,连接CH,AH,AF.
∵DF=DC,∴DE是△FCH的中位线.∴DE∥CH,CH=2DE.
由旋转的性质,得DE=DM,∠MDE=2α.∴∠FCH=2α.
∵∠B=∠ACB=α,∴∠ACH=α,△ABC是等腰三角形.
∴∠B=∠ACH,AB=AC.
设DM=DE=m,CD=n,则CH=2m,CM=m+n,DF=CD=n.
∴FM=DF-DM=n-m.
∵AM⊥BC,∴BM=CM=m+n.
∴BF=BM-FM=m+n-(n-m)=2m.
∴CH=BF.
在△ABF和△ACH中,
∴△ABF≌△ACH(SAS).∴AF=AH.
∵FE=EH,∴AE⊥FH,即∠AEF=90°.
(2023·濮阳二模)如图,在Rt△ABO中,∠OAB=90°,点A在x轴的正半轴上,B点坐标为(2,4),反比例函数y=(x>0)的图象过斜边OB的中点D,交AB于点C.
(1)求反比例函数的解析式及△OBC的面积;
解:(1)∵B(2,4),点D为OB的中点,∴OA=2,AB=4,D(1,2).
把D(1,2)代入y=,得k=2.
∴反比例函数的解析式为y=(x>0).
∵C在AB上,∠OAB=90°,∴设点C(2,m),代入y=,得m=1.
∴C(2,1).∴AC=1.∴BC=AB-AC=3.
∴S△OBC=OA·BC=×2×3=3.
(2)将Rt△ABO沿x轴向右平移到△A′B′O′的位置,若四边形OBB′O′是菱形,求B′O′与y=(x>0)图象的交点E的坐标.
(2)在Rt△OAB中,OA=2,AB=4,
∴OB===2.
∵四边形OBB′O′是菱形,
∴O′(2,0),B′(2+2,4).
设直线B′O′的解析式为y=k1x+b1(k1≠0).
把O′(2,0),B′(2+2,4)代入y=k1x+b1,
得 解得
∴直线B′O′的解析式为y=2x-4.
∵直线B′O′与反比例函数图象的交点为E,
∴联立,得
解得(负值已舍去)
∴E(+,2-2).
(2023·萍乡模拟)如图,在平面直角坐标系中,△ABC的边AB在y轴上,AC∥x轴,点C的坐标为(4,6),AB=3,将△ABC向下方平移,得到△DEF,且点A的对应点D落在反比例函数y=(x>0)图象上,点B的对应点E落在x轴上,连接OD,OD∥BC.
(1)求证:四边形ODFE为平行四边形;
(1)证明:由平移的性质,可知BC∥EF,AC∥DF,AB∥DE.
∵AC∥x轴,且OE在x轴上,
∴AC∥OE.∴DF∥OE.
∵OD∥BC,BC∥EF,∴OD∥EF.
∴四边形ODFE为平行四边形.
(2)求反比例函数y=(x>0)的表达式;
(2)解:连接CD,如图.
∵四边形ODFE为平行四边形,∴OD=EF=BC.
又∵OD∥BC,∴四边形BCDO是平行四边形.
∴CD=OB,CD∥AB.
∵DE∥AB,∴C,D,E三点共线.
∴CE∥AO.
∵AC∥OE,∴四边形ACEO是平行四边形.
∴OE=AC.
∵点C的坐标为(4,6),AB=3,∴OE=AC=4,DE=AB=3.
∴点D的坐标为(4,3).
∵点D在反比例函数y=(x>0)的图象上,∴k=4×3=12.
∴反比例函数的表达式为y=(x>0).
(3)求△ABC平移的距离及线段BC扫过的面积.
(3)解:连接BE,CF,如图.
在Rt△BOE中,OB=OA-AB=6-3=3,OE=4,
∴BE===5.
∴△ABC平移的距离为5.
∵BC∥EF,BC=EF,∴四边形BCFE是平行四边形.
∴S BCFE=2S△BCE=2×CE·OE=2××6×4=24.
∴线段BC扫过的面积为24.
第二部分 专题复习
专题七 图形的折叠、旋转与平移
(2023·达州改编)如图,网格中每个小正方形的边长均为1,△ABC的顶点均在小正方形的格点上.
(1)将△ABC向下平移3个单位长度得到△A1B1C1,画出△A1B1C1;
解:(1)△A1B1C1即为所求,如图.
(2)将△ABC绕点C顺时针旋转90度得到△A2B2C,画出△A2B2C;
解:(2)△A2B2C即为所求,如图.
(3)在(2)的运动过程中请计算出△ABC扫过的面积;
(3)S△ABC=2×3-×2×1-×2×1-×3×1=.
∵AC==,∴S扇形AC ) ==.
∴在(2)的运动过程中△ABC扫过的面积为S=S△ABC+S扇形AC =.
(4)作△A2B2C关于直线l的轴对称图形△A3B3C.
(4)△A3B3C即为所求,如图.
(2023·凉山州)如图,在Rt△ABC纸片中,∠ACB=90°,CD是AB边上的中线,将△ACD沿CD折叠,当点A落在点A′处时,恰好CA′⊥AB,若BC=2,则CA′= 2 .
2
(2023·娄底)如图,点E在矩形ABCD的边CD上,将△ADE沿AE折叠,点D恰好落在边BC上的点F处,若BC=10,sin ∠AFB=,则DE= 5 .
5
(2021·广东)如图,边长为1的正方形ABCD中,点E为AD的中点.连接BE,将△ABE沿BE折叠得到△FBE,BF交AC于点G,求CG的长.
解:如图,延长BF交CD于点H,连接EH.
∵四边形ABCD是正方形,
∴AB∥CD,∠D=∠DAB=90°,AD=CD=AB=1.
∴AC===.
由翻折的性质可知,AE=EF,∠EAB=∠EFB=90°,∠3=∠4.
∵点E是AD的中点,∴AE=DE=EF=.
在Rt△EHD和Rt△EHF中,
∴Rt△EHD≌Rt△EHF(HL).∴∠1=∠2.
∵∠DEF+∠AEF=180°,∴2∠1+2∠3=180°.
∴∠1+∠3=90°.
∵∠3+∠5=90°,∴∠1=∠5.
∴△EDH∽△BAE.
∴==. ∴DH=. ∴CH=.
∵CH∥AB,∴△CHG∽△ABG.
∴==.
∴CG=AC=.
(2022·深圳节选)(1)发现:如图1所示,在正方形ABCD中,E为AD边上一点,将△AEB沿BE翻折到△BEF处,延长EF交CD边于G点.求证:△BFG≌△BCG;
(1)证明:∵将△AEB沿BE翻折得到
△FEB,四边形ABCD是正方形,
∴BF=AB,∠BFE=∠A=∠C=90°.
∴∠BFG=90°=∠C.
∵AB=BC=BF,BG=BG,
∴Rt△BFG≌Rt△BCG(HL).
(2)探究:如图2,在矩形ABCD中,E为AD边上一点,且AD=8,AB=6.将△AEB沿BE翻折到△BEF处,延长EF交BC边于点G,延长BF交CD边于点H,且FH=CH,求AE的长.
(2)解:延长BH,AD交于点Q,如图.
设FH=CH=x,则BH=6+x.
在Rt△BCH中,BC2+CH2=BH2,
即82+x2=(6+x)2.解得x=.
∴DH=DC-CH=.
∵∠BFG=∠BCH=90°,∠GBF=∠HBC,∴△BFG∽△BCH.
∴==,即==.
∴BG=,FG=.
∵DQ∥CB,∴△DHQ∽△CHB.
∴=,即=. ∴QD=.
设AE=EF=m,则DE=8-m.
∴EQ=DE+QD=8-m+=-m.
∵EQ∥GB,∴△EFQ∽△GFB.
∴=,即=.解得m=.
∴AE的长为.
(毕节中考)如图1,在Rt△ABC中,∠BAC=90°,AB=AC,D为△ABC内一点,将线段AD绕点A逆时针旋转90°得到AE,连接CE,BD的延长线与CE交于点F.
(1)求证:BD=CE,BD⊥CE;
(1)证明:如答图1,设AC与BF交于点O.
∵线段AD绕点A逆时针旋转90°得到AE,
∴AD=AE,∠DAE=90°.
∵∠BAC=90°,∴∠BAC=∠DAE.∴∠BAD=∠CAE.
在△ABD和△ACE中,
∴△ABD≌△ACE(SAS).∴BD=CE,∠ABD=∠ACE.
又∵∠AOB=∠COF,∴∠BFC=∠BAC=90°.∴BD⊥CE.
(2)如图2,连接AF,DC,已知∠BDC=135°,判断AF与DC的位置关系,并说明理由.
(2)解:AF∥DC.
理由如下:如答图2,过点A作AG⊥BF于点G,AH⊥CE于点H.
由(1)知△ABD≌△ACE.
∴BD=CE,S△ABD=S△ACE.
∴BD·AG=CE·AH. ∴AG=AH.
又∵AG⊥BF,AH⊥CE, ∴FA平分∠BFE.
又∵∠BFE=90°,∴∠AFD=45°.
∵∠BDC=135°,∴∠FDC=45°.
∴∠AFD=∠FDC.∴AF∥DC.
(2023·自贡)如图1,一大一小两个等腰直角三角形叠放在一起,M,N分别是斜边DE,AB的中点,DE=2,AB=4.
(1)将△CDE绕顶点C旋转一周,请直接写出点M,N距离的最大值和最小值;
解:(1)如答图1,以C为圆心,CM长为半径画圆,连接CN交DE于M1,延长NC交⊙C于M2.
∵△ACB是等腰直角三角形,N是AB的中点,
∴CN平分∠ACB,CN=AB=×4=2.
∵△DCE是等腰直角三角形,
∴M1是DE的中点.∴CM1=DE=×2=1.
∴点M,N距离的最小值是NM1=CN-CM1=2-1=1,点M,N距离的最大值是NM2=CN+CM2=2+1=3.
(2)将△CDE绕顶点C逆时针旋转120°(如图2),求MN的长.
(2)如答图2,连接CM,CN,作NH⊥MC交MC的延长线于点H.
∵△ACB是等腰直角三角形,点N是AB的中点,
∴CN=AB=2.同理,CM=DE=1.
∵△CDE绕顶点C逆时针旋转120°,∴∠MCN=120°.
∴∠NCH=180°-∠MCN=60°.
∴CH=CN=1.∴NH==.
∵MH=MC+CH=2,∴MN==.
(广东中考节选)如图,在平面直角坐标系中,抛物线y=x2+x-与x轴交于点A,B(点A在点B右侧),点D为抛物线的顶点,点C在y轴的正半轴上,CD交x轴于点F,△CAD绕点C顺时针旋转得到△CFE,点A恰好旋转到点F,连接BE.
(1)解:令x2+x-=0,解得x1=1,x2=-7.
∴A(1,0),B(-7,0).
由y=x2+x-=(x+3)2-2,得D(-3,-2).
(1)求点A,B,D的坐标;
(2)求证:四边形BFCE是平行四边形.
(2)证明:∵△CAD绕点C顺时针旋转得到△CFE,
∴∠ACF=∠ECF,CF=CA.
∵CO⊥AF,∴OF=OA=1.
∴F(-1,0).又D(-3,-2),
易求得直线DF的解析式为y=x+.
当x=0时,y=.
∴C(0,).
∴OC=.
∴CA=CF==2.
又FA=2,∴△ACF是等边三角形.
∴∠AFC=∠ACF.
∴∠ECF=∠ACF=∠AFC=60°.
∴EC∥BF.
∵EC=DC==6,BF=6,∴EC=BF.
∴四边形BFCE是平行四边形.
(2023·北京)在△ABC中,∠B=∠C=α(0°<α<45°),AM⊥BC于点M,D是线段MC上的动点(不与点M,C重合),将线段DM绕点D顺时针旋转2α得到线段DE.
(1)如图1,当点E在线段AC上时,求证:点D是MC的中点;
(1)证明:由旋转的性质,得DM=DE,∠MDE=2α.
∵∠C=α,∴∠DEC=∠MDE-∠C=α.
∴∠C=∠DEC.∴DE=DC.
∴DM=DC,即点D是MC的中点.
(2)如图2,若在线段BM上存在点F(不与点B,M重合)满足DF=DC,连接AE,EF,直接写出∠AEF的大小,并证明.
(2)解:∠AEF=90°.证明如下:
如图,延长FE到H使EH=FE,连接CH,AH,AF.
∵DF=DC,∴DE是△FCH的中位线.∴DE∥CH,CH=2DE.
由旋转的性质,得DE=DM,∠MDE=2α.∴∠FCH=2α.
∵∠B=∠ACB=α,∴∠ACH=α,△ABC是等腰三角形.
∴∠B=∠ACH,AB=AC.
设DM=DE=m,CD=n,则CH=2m,CM=m+n,DF=CD=n.
∴FM=DF-DM=n-m.
∵AM⊥BC,∴BM=CM=m+n.
∴BF=BM-FM=m+n-(n-m)=2m.
∴CH=BF.
在△ABF和△ACH中,
∴△ABF≌△ACH(SAS).∴AF=AH.
∵FE=EH,∴AE⊥FH,即∠AEF=90°.
(2023·濮阳二模)如图,在Rt△ABO中,∠OAB=90°,点A在x轴的正半轴上,B点坐标为(2,4),反比例函数y=(x>0)的图象过斜边OB的中点D,交AB于点C.
(1)求反比例函数的解析式及△OBC的面积;
解:(1)∵B(2,4),点D为OB的中点,∴OA=2,AB=4,D(1,2).
把D(1,2)代入y=,得k=2.
∴反比例函数的解析式为y=(x>0).
∵C在AB上,∠OAB=90°,∴设点C(2,m),代入y=,得m=1.
∴C(2,1).∴AC=1.∴BC=AB-AC=3.
∴S△OBC=OA·BC=×2×3=3.
(2)将Rt△ABO沿x轴向右平移到△A′B′O′的位置,若四边形OBB′O′是菱形,求B′O′与y=(x>0)图象的交点E的坐标.
(2)在Rt△OAB中,OA=2,AB=4,
∴OB===2.
∵四边形OBB′O′是菱形,
∴O′(2,0),B′(2+2,4).
设直线B′O′的解析式为y=k1x+b1(k1≠0).
把O′(2,0),B′(2+2,4)代入y=k1x+b1,
得 解得
∴直线B′O′的解析式为y=2x-4.
∵直线B′O′与反比例函数图象的交点为E,
∴联立,得
解得(负值已舍去)
∴E(+,2-2).
(2023·萍乡模拟)如图,在平面直角坐标系中,△ABC的边AB在y轴上,AC∥x轴,点C的坐标为(4,6),AB=3,将△ABC向下方平移,得到△DEF,且点A的对应点D落在反比例函数y=(x>0)图象上,点B的对应点E落在x轴上,连接OD,OD∥BC.
(1)求证:四边形ODFE为平行四边形;
(1)证明:由平移的性质,可知BC∥EF,AC∥DF,AB∥DE.
∵AC∥x轴,且OE在x轴上,
∴AC∥OE.∴DF∥OE.
∵OD∥BC,BC∥EF,∴OD∥EF.
∴四边形ODFE为平行四边形.
(2)求反比例函数y=(x>0)的表达式;
(2)解:连接CD,如图.
∵四边形ODFE为平行四边形,∴OD=EF=BC.
又∵OD∥BC,∴四边形BCDO是平行四边形.
∴CD=OB,CD∥AB.
∵DE∥AB,∴C,D,E三点共线.
∴CE∥AO.
∵AC∥OE,∴四边形ACEO是平行四边形.
∴OE=AC.
∵点C的坐标为(4,6),AB=3,∴OE=AC=4,DE=AB=3.
∴点D的坐标为(4,3).
∵点D在反比例函数y=(x>0)的图象上,∴k=4×3=12.
∴反比例函数的表达式为y=(x>0).
(3)求△ABC平移的距离及线段BC扫过的面积.
(3)解:连接BE,CF,如图.
在Rt△BOE中,OB=OA-AB=6-3=3,OE=4,
∴BE===5.
∴△ABC平移的距离为5.
∵BC∥EF,BC=EF,∴四边形BCFE是平行四边形.
∴S BCFE=2S△BCE=2×CE·OE=2××6×4=24.
∴线段BC扫过的面积为24.
同课章节目录
