2023-2024学年数学七年级下册 第9章 平行线单元测试试题(青岛版)提升卷(含解析)
文档属性
| 名称 | 2023-2024学年数学七年级下册 第9章 平行线单元测试试题(青岛版)提升卷(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-29 15:35:50 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
2023-2024学年数学七年级平行线(青岛版)
单元测试 提升卷 含解析
学校:___________姓名:___________班级:___________考号:___________
评卷人得分
一、单选题(共30分)
1.(本题3分)下列语句中叙述正确的有( )
①相等的角是对顶角;
②过一点有且只有一条直线与已知直线平行;
③若与相交,与相交,则与相交;
④两条直线被第三条直线所截,同旁内角互补;
⑤直线外一点到这条直线的垂线段,叫做点到直线的距离.
A.0个 B.1个 C.2个 D.3个
2.(本题3分)如图,,则的度数是( )
A. B. C. D.
3.(本题3分)如图,,连接,E是线段上一动点,、分别平分、,若,则的度数用含α的式子表示为( )
A. B. C. D.
4.(本题3分)如图,下列结论错误的是( )
A.与是邻补角 B.与是同位角
C.与是内错角 D.与是同旁内角
5.(本题3分)若与的两边分别平行,且,,则的度数为( )
A. B. C.或 D.或
6.(本题3分)如图,,平分,平分,,则下列结论:①;②;③;④;⑤.其中正确的结论有( )
A.1个 B.2个 C.3个 D.4个
7.(本题3分)如图是一盏可调节台灯及其示意图.固定支撑杆垂直底座于点,与是分别可绕点和旋转的调节杆,台灯灯罩可绕点旋转调节光线角度,在调节过程中,最外侧光线、组成的始终保持不变.现调节台灯,使外侧光线,,若,则( )
A. B. C. D.
8.(本题3分)一根直尺和一个含角的直角三角板按如图方式叠合在一起,若,则的度数是( )
A. B. C. D.
9.(本题3分)如图,直线上有两点A、C,分别引两条射线、.,与在直线异侧.若,射线、分别绕A点,C点以1度/秒和6度/秒的速度同时顺时针转动,设时间为t秒,在射线转动一周的时间内,当时间t的值为( )时,与平行.( )
A.4秒 B.10秒 C.40秒 D.4或40秒
10.(本题3分)如图,直线,. 其中,,则的最大整数值是( )
A.109° B.110° C. D.
评卷人得分
二、填空题(共24分)
11.(本题3分)一大门的栏杆如图所示,垂直地面于点A,平行于地面,则 .
12.(本题3分)如图,将木条a、b与c钉在一起,,转动木条a改变的度数,若要使木条a与b平行,则的度数应为 .
13.(本题3分)如图,已知,分别交,于点E,F,,则 .
14.(本题3分)将两张长方形纸片按如图所示摆放,使其中一张长方形纸片的一个顶点恰好落在另一张长方形纸片的一条边上,若,则 .
15.(本题3分)如图,直线和是两条互相平行的直线,点和分别在直线和上,是平面内一点(不在两条直线上),满足,,则 度.
16.(本题3分)如图,,直线交,于点,把一块含的三角板按如图所示位置摆放,测得,则 .
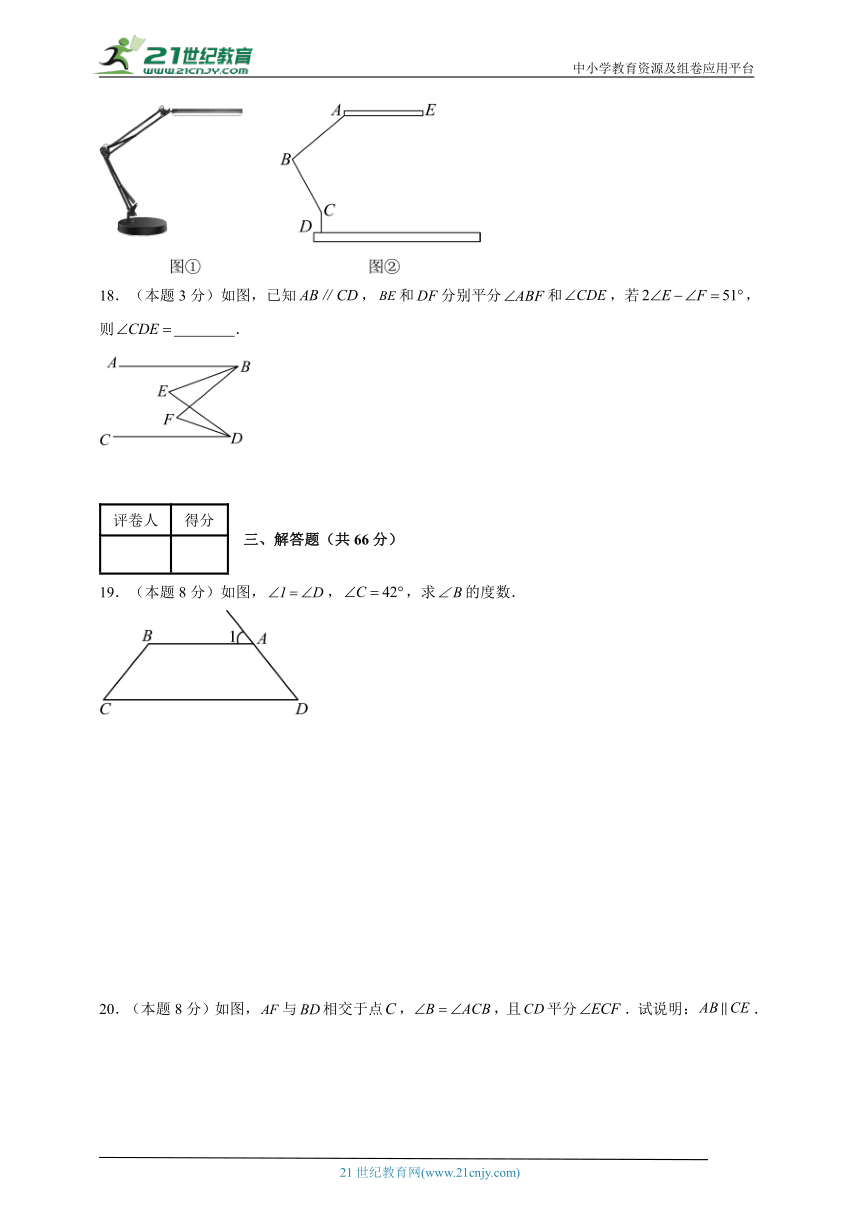
17.(本题3分)图①是小明写字桌上的一款长臂折叠护眼台灯,支柱与桌面垂直,小明将台灯的灯管高度调节后如图②所示. 已知此时灯管与桌面平行, , ,则调节杆和的夹角 .
18.(本题3分)如图,已知,和分别平分和,若,则 .
评卷人得分
三、解答题(共66分)
19.(本题8分)如图,,,求的度数.
20.(本题8分)如图,与相交于点,,且平分.试说明:.
21.(本题10分)如图,直线c,d分别截直线a,b,已知,,求和的度数.
22.(本题10分)如图,,,,平分交于点.
(1)求的度数;
(2)试说明.
23.(本题10分)图1是一种网红弹弓的实物图,在两边系上皮筋,拉动皮筋可形成如图2的平面示意图,弹弓的两边可看成是平行的,即,现测得,.过点P作,如图3.
(1)求的度数;
(2)根据下面的信息窗.判断此次瞄准是否最准确.
信息窗 当拉起皮筋使时,瞄准最准确
24.(本题10分)已知与,其中是锐角,设,.
(1)若,:
①如下图,此时与的数量关系是_________;
②实际上除了①中的图形.还有另外一种情况,请在下面给出的基础上画出相应的,并求出与的数量关系;
(2)若,,,直接写出的值.
25.(本题10分)如图,灯A射线从开始顺时针旋转至便立即回转,灯B射线从开始顺时针旋转至便立即回转,两灯不停交叉照射巡视,若灯A转动的速度是每秒,灯B转动的速度是每秒.假定主道路是平行的,即,且.
(1)填空:
(2)若灯B射线先转动30秒,灯A射线才开始转动,在灯B射线到达之前,A灯转动几秒,两灯的光束互相平行?
(3)若两灯同时开始转动,两灯射出的光束交于点C,且,则在灯B射线到达之前,转动的时间为______秒.
参考答案:
1.A
【分析】本题主要考查了平行线的性质,对顶角,点到直线的距离及平行公理的概念;根据对顶角的概念、平行公理、平行线的性质、点到直线的距离逐一判定.
【详解】
解:①相等的角不一定是对顶角;①错误;
②经过直线外一点,有且只有一条直线与已知直线平行;②错误;
③若与相交,与相交,则与不一定相交;③错误;
④两条平行直线被第三条直线所截,同旁内角互补;④错误;
⑤直线外一点到这条直线的垂线段的长度,叫做点到直线的距离;⑤错误.
故选:A.
2.C
【分析】
本题考查平行线的性质,对顶角相等,掌握平行线的性质是解题关键.根据“两直线平行,同旁内角互补”可求出,再根据对顶角相等求解即可.
【详解】解:∵,
∴,
∴.
故选:C.
3.A
【分析】
本题考查了角平分线的定义,平行线的性质,熟练掌握两直线平行,内错角相等是解题关键.过点作,过点作,根据平行线的性质和角平分线的定义求解即可.
【详解】解:如图,过点作,过点作,
,
,,
,
,
、分别平分、,
,,
,
,,
,
故选:A.
4.C
【分析】
本题考查了邻补角、同位角、内错角、同旁内角的定义,根据邻补角、同位角、内错角、同旁内角的定义逐项分析即可求解.
【详解】解:A、两个角有一条公共边,且它们的另一边互为反向延长线,具有这种关系的两个角,互为邻补角;故与是邻补角;A选项不符合题意;
B、两条直线,被第三条直线所截,在截线的同旁,且在被截两直线,的同一侧的角,我们把这样的两个角称为同位角;故与是同位角;B选项不符合题意;
C、两条直线被第三条直线所截,两个角分别在截线的两侧,且夹在两条被截直线之间,具有这样位置关系的一对角叫做内错角;故与不是内错角;C选项符合题意;
D、两条直线被第三条直线所截,在截线同旁,且在被截线之内的两角,叫做同旁内;故与是同旁内角;D选项不符合题意;
故选:C.
5.C
【分析】
本题考查平行线的性质,分两种情况进行讨论求解即可.
【详解】解:当两角相等时,如图,
∴,
解得:,
∴;
当两角互补时,如图:
∴,
解得:,
∴;
故选C.
6.D
【分析】
本题考查平行线的性质,垂线,解题的关键是熟练掌握平行线的性质定理.
由可得,由平分可得,故①不正确,⑤正确;由平分,平分,可得,故②正确;由可得,从而可得,故③正确;由可得,从而可得,
由可得,可得,故④正确.
【详解】解:,
,
平分,
,
故①不正确,⑤正确;
平分,平分,
,
,
,
∴,故②正确;
,
,故③正确;
,
,
,
,
,
,故④正确.
故正确结论为:②③④⑤,
故选:D.
7.B
【分析】
本题主要考查了平行线的性质与判定,如图所示,过点A作,过点B作,则,由得到,则,进而得到,再根据平行线的性质得到,由此即可得到.正确作出辅助线是解题的关键.
【详解】解:如图所示,过点A作,过点B作,
∵,
∴,
∵,
∴,即,
∵,
∴,
∴,
∵,,
∴,
∴,
∴,
故选:B.
8.D
【分析】
本题考查了平行线的性质,三角板中角度的求解,先根据平角的定义求出的度数,再利用两直线平行同位角相等即可求解.
【详解】解:如图,
,
,
,
故选:D.
9.D
【分析】分情况讨论:①与在的两侧,分别表示出与,然后根据内错角相等两直线平行,列式计算即可得解;②旋转到与都在的右侧,分别表示出与,然后根据同位角相等两直线平行,列式计算即可得解;③旋转到与都在的左侧,分别表示出与,然后根据同位角相等两直线平行,列式计算即可得解.
【详解】解:分三种情况:
如图①,与在的两侧时,
∵,,
∴,,
要使,则,
即,
解得;
此时,
∴;
②旋转到与都在的右侧时,
∵,,
要使,则,
即,
解得,
此时,
∴;
③旋转到与都在的左侧时,
∴,,
要使,则,
即,
解得,
此时,
而,
∴此情况不存在.
综上所述,当时间t的值为4秒或40秒时,与平行.
故选:D.
【点睛】本题考查了平行线的判定,读懂题意并熟练掌握平行线的判定方法是解题的关键,要注意分情况讨论.
10.A
【分析】先添加辅助线,再根据平行线的性质和三角形外角性质,求出与的关系式,最后由,即可求出范围,得出答案.
【详解】如图,延长,分别交和于点,,
∵,,
∴,
∵,
∴,
∵,,,
∴,
∴,
∴,整理得:,
∴,
解得:,
∴的最大整数值是.
故选:.
【点睛】本题考查了平行线的性质,三角形外角性质的应用,解题的关键是熟练掌握平行线的性质及等角度的转换.
11.
【分析】
本题主要考查了平行线的性质,两直线平行,同旁内角互补.正确作出辅助线是解题的关键.过B作,则.根据平行线的性质即可求解.
【详解】
解:过B作,
∵,
∴,
∴,
又∵,
∴,
∴,
∴.
故答案为:.
12./度;
【分析】
本题考查平行线的性质,根据两直线平行同位角相等即可得到答案;
【详解】解:∵,,
∴,
故答案为:.
13.59
【分析】
本题考查了直线平行的性质:两直线平行,同位角相等.也考查了对顶角的性质.根据两直线平行,同位角相等得到,再根据对顶角相等得,从而求出的度数.
【详解】解:,
,
,,
,
故答案为:59.
14./
【分析】
本题考查平行线的性质,根据两直线平行内错角相等即可得到答案;
【详解】解:过作,
由题意可得,
,
∵,
∴,
∴,,
∵,,
∴,
故答案为:.
15.
【分析】
本题考查了平行线的判定和性质,熟练掌握“平行于同一条直线的两直线平行”是解题的关键.
过点作,根据平行于同一条直线的两直线平行可得,根据两直线平行,内错角相等可得,求得,根据两直线平行,同旁内角互补即可求解.
【详解】解:如图:过点作,则,
∵,,
∴,
则,
∵,
∴;
故答案为:.
16.15
【分析】
本题主要考查了平行线的性质、角的和差等知识点,掌握两直线平行、内错角相等成为解题的关键.
由邻补角的定义可得,根据,然后根据角的和差即可解答.
【详解】解:∵,
∴,
∵,
∴,
∴.
故答案为:15.
17./100度
【分析】本题考查平行线的判定和性质.解题的关键是过拐点构造平行线.过点作,过点作,根据平行线的性质分别求出,,进而可求出的度数.
【详解】解:过点作,过点作,
∴,
∵,
∴.
∵ ,,,
∴,,
∵,
∴,
∴,
∴,
故答案为:.
18./度
【分析】过作,过作,可得,,,,,即可求解.
【详解】解:如图,过作,过作,
,
,
,,
,,
设,,
,,
和分别平分和,
, ,
,,
,
,
,
,
解得:,
;
故答案:.
【点睛】本题考查了平行线的性质,掌握性质,作出适当的辅助线是解题的关键.
19.
【分析】
本题主要考查平等线的判定与性质,由得出,由得,从而可得答案.
【详解】解:∵,
∴,
∴,
∵,
∴.
20.见解析
【分析】
本题考查了平行线的判定,掌握“同位角相等,两直线平行”是解题的关键.根据角平分线的定义结合对顶角得到,则可证明,根据平行线的判定即可证明.
【详解】
证明:因为平分,
所以.
因为,
所以.
因为,
所以.
所以.
21.,
【分析】
本题考查了平行线的判定和性质,邻补角的性质,掌握平行线的判定和性质是解题的关键.
根据证明,再利用平行线的性质求解即可.
【详解】解:∵,
∴,
∴,
∴.
22.(1)
(2)见解析
【分析】
本题主要考查了平行线的性质与判定,角平分线的定义,熟知平行线的性质与判定条件是解题的关键.
(1)由可得,进而可得的度数;
(2)由可得,结合平分,可得,再由平行线的判定,即可得出结论.
【详解】(1)解:∵,
∴,
∵,
∴.
(2)解:∵,
∴,
∴,
∵平分,
∴,
∴,
∴.
23.(1)
(2)不是最准确的
【分析】
本题考查的是平行线的性质,平行公理的应用,熟记两直线平行,同旁内角互补是解本题的关键.
(1)由,可得,根据可得;
(2)证明,可得,从而可得结论.
【详解】(1)解:,
.
,
.
,
;
(2)解:,,
.
.
.
,
此次瞄准不是最准确的.
24.(1)①;②图见解析,
(2)或
【分析】本题考查平行线的性质,解答时需要一定的灵活变换图形的能力,以及探究能力.
(1)①根据,,由两直线平行,同位角相等即可得到,利用等量代换即可得到,即可得出结论;②根据,,画出与射线延伸方向相反的情况,即可探究出α与β的另一种数量关系,再利用平行线的性质说明理由即可;
(2)根据题意,画出符合题意的两个图形,再利用平行线的性质探究出结论即可.
【详解】(1)解:①∵,
∴,
∵,
∴,
∴,
故答案为:;
②α与β的数量关系还可能是:.
图形如下:
理由如下:
∵,
∴,
∵,
∴,即;
(2)解:设的垂足为D.
情况1:如图,
∵,,
∴,
∵,
∴,即,
;
情况2:如图,
反向延长得,
由情况1,知,
∵,
∴,
整理,得,
,
综上,的值为:或.
25.(1)60
(2)A灯旋转30秒或110秒时,两灯的光束互相平行
(3)60或140或100
【分析】
本题主要考查了平行线的性质以及角的和差关系的运用,解决问题的关键是运用分类思想进行求解,解题时注意:两直线平行,内错角相等;两直线平行,同旁内角互补.
(1)根据,,即可得到的度数;
(2)设A灯转动t秒,两灯的光束互相平行,分两种情况进行讨论∶当时,根据,可得;当时,根据,可得;
(3)分两种情形,根据平行线的性质,构建方程解决问题即可.
【详解】(1)解:,,
.
故答案为:.
(2)设A灯转动t秒.两灯的光束互相平行,
①当时,如图1
,
,
,
,
,
,
解得:;
②当时,如图2,
,
,
,
,
解得:,
综上所述,A灯旋转30秒或110秒时.两灯的光束互相平行.
(3)设灯A射线转动时间为t秒,
,
,
又,
,
解得:(舍去)
或,
解得,
如图4中,当时
,
,
综上所述:满足条件的值为60或140或100秒.
故答案为:60或140或100.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2023-2024学年数学七年级平行线(青岛版)
单元测试 提升卷 含解析
学校:___________姓名:___________班级:___________考号:___________
评卷人得分
一、单选题(共30分)
1.(本题3分)下列语句中叙述正确的有( )
①相等的角是对顶角;
②过一点有且只有一条直线与已知直线平行;
③若与相交,与相交,则与相交;
④两条直线被第三条直线所截,同旁内角互补;
⑤直线外一点到这条直线的垂线段,叫做点到直线的距离.
A.0个 B.1个 C.2个 D.3个
2.(本题3分)如图,,则的度数是( )
A. B. C. D.
3.(本题3分)如图,,连接,E是线段上一动点,、分别平分、,若,则的度数用含α的式子表示为( )
A. B. C. D.
4.(本题3分)如图,下列结论错误的是( )
A.与是邻补角 B.与是同位角
C.与是内错角 D.与是同旁内角
5.(本题3分)若与的两边分别平行,且,,则的度数为( )
A. B. C.或 D.或
6.(本题3分)如图,,平分,平分,,则下列结论:①;②;③;④;⑤.其中正确的结论有( )
A.1个 B.2个 C.3个 D.4个
7.(本题3分)如图是一盏可调节台灯及其示意图.固定支撑杆垂直底座于点,与是分别可绕点和旋转的调节杆,台灯灯罩可绕点旋转调节光线角度,在调节过程中,最外侧光线、组成的始终保持不变.现调节台灯,使外侧光线,,若,则( )
A. B. C. D.
8.(本题3分)一根直尺和一个含角的直角三角板按如图方式叠合在一起,若,则的度数是( )
A. B. C. D.
9.(本题3分)如图,直线上有两点A、C,分别引两条射线、.,与在直线异侧.若,射线、分别绕A点,C点以1度/秒和6度/秒的速度同时顺时针转动,设时间为t秒,在射线转动一周的时间内,当时间t的值为( )时,与平行.( )
A.4秒 B.10秒 C.40秒 D.4或40秒
10.(本题3分)如图,直线,. 其中,,则的最大整数值是( )
A.109° B.110° C. D.
评卷人得分
二、填空题(共24分)
11.(本题3分)一大门的栏杆如图所示,垂直地面于点A,平行于地面,则 .
12.(本题3分)如图,将木条a、b与c钉在一起,,转动木条a改变的度数,若要使木条a与b平行,则的度数应为 .
13.(本题3分)如图,已知,分别交,于点E,F,,则 .
14.(本题3分)将两张长方形纸片按如图所示摆放,使其中一张长方形纸片的一个顶点恰好落在另一张长方形纸片的一条边上,若,则 .
15.(本题3分)如图,直线和是两条互相平行的直线,点和分别在直线和上,是平面内一点(不在两条直线上),满足,,则 度.
16.(本题3分)如图,,直线交,于点,把一块含的三角板按如图所示位置摆放,测得,则 .
17.(本题3分)图①是小明写字桌上的一款长臂折叠护眼台灯,支柱与桌面垂直,小明将台灯的灯管高度调节后如图②所示. 已知此时灯管与桌面平行, , ,则调节杆和的夹角 .
18.(本题3分)如图,已知,和分别平分和,若,则 .
评卷人得分
三、解答题(共66分)
19.(本题8分)如图,,,求的度数.
20.(本题8分)如图,与相交于点,,且平分.试说明:.
21.(本题10分)如图,直线c,d分别截直线a,b,已知,,求和的度数.
22.(本题10分)如图,,,,平分交于点.
(1)求的度数;
(2)试说明.
23.(本题10分)图1是一种网红弹弓的实物图,在两边系上皮筋,拉动皮筋可形成如图2的平面示意图,弹弓的两边可看成是平行的,即,现测得,.过点P作,如图3.
(1)求的度数;
(2)根据下面的信息窗.判断此次瞄准是否最准确.
信息窗 当拉起皮筋使时,瞄准最准确
24.(本题10分)已知与,其中是锐角,设,.
(1)若,:
①如下图,此时与的数量关系是_________;
②实际上除了①中的图形.还有另外一种情况,请在下面给出的基础上画出相应的,并求出与的数量关系;
(2)若,,,直接写出的值.
25.(本题10分)如图,灯A射线从开始顺时针旋转至便立即回转,灯B射线从开始顺时针旋转至便立即回转,两灯不停交叉照射巡视,若灯A转动的速度是每秒,灯B转动的速度是每秒.假定主道路是平行的,即,且.
(1)填空:
(2)若灯B射线先转动30秒,灯A射线才开始转动,在灯B射线到达之前,A灯转动几秒,两灯的光束互相平行?
(3)若两灯同时开始转动,两灯射出的光束交于点C,且,则在灯B射线到达之前,转动的时间为______秒.
参考答案:
1.A
【分析】本题主要考查了平行线的性质,对顶角,点到直线的距离及平行公理的概念;根据对顶角的概念、平行公理、平行线的性质、点到直线的距离逐一判定.
【详解】
解:①相等的角不一定是对顶角;①错误;
②经过直线外一点,有且只有一条直线与已知直线平行;②错误;
③若与相交,与相交,则与不一定相交;③错误;
④两条平行直线被第三条直线所截,同旁内角互补;④错误;
⑤直线外一点到这条直线的垂线段的长度,叫做点到直线的距离;⑤错误.
故选:A.
2.C
【分析】
本题考查平行线的性质,对顶角相等,掌握平行线的性质是解题关键.根据“两直线平行,同旁内角互补”可求出,再根据对顶角相等求解即可.
【详解】解:∵,
∴,
∴.
故选:C.
3.A
【分析】
本题考查了角平分线的定义,平行线的性质,熟练掌握两直线平行,内错角相等是解题关键.过点作,过点作,根据平行线的性质和角平分线的定义求解即可.
【详解】解:如图,过点作,过点作,
,
,,
,
,
、分别平分、,
,,
,
,,
,
故选:A.
4.C
【分析】
本题考查了邻补角、同位角、内错角、同旁内角的定义,根据邻补角、同位角、内错角、同旁内角的定义逐项分析即可求解.
【详解】解:A、两个角有一条公共边,且它们的另一边互为反向延长线,具有这种关系的两个角,互为邻补角;故与是邻补角;A选项不符合题意;
B、两条直线,被第三条直线所截,在截线的同旁,且在被截两直线,的同一侧的角,我们把这样的两个角称为同位角;故与是同位角;B选项不符合题意;
C、两条直线被第三条直线所截,两个角分别在截线的两侧,且夹在两条被截直线之间,具有这样位置关系的一对角叫做内错角;故与不是内错角;C选项符合题意;
D、两条直线被第三条直线所截,在截线同旁,且在被截线之内的两角,叫做同旁内;故与是同旁内角;D选项不符合题意;
故选:C.
5.C
【分析】
本题考查平行线的性质,分两种情况进行讨论求解即可.
【详解】解:当两角相等时,如图,
∴,
解得:,
∴;
当两角互补时,如图:
∴,
解得:,
∴;
故选C.
6.D
【分析】
本题考查平行线的性质,垂线,解题的关键是熟练掌握平行线的性质定理.
由可得,由平分可得,故①不正确,⑤正确;由平分,平分,可得,故②正确;由可得,从而可得,故③正确;由可得,从而可得,
由可得,可得,故④正确.
【详解】解:,
,
平分,
,
故①不正确,⑤正确;
平分,平分,
,
,
,
∴,故②正确;
,
,故③正确;
,
,
,
,
,
,故④正确.
故正确结论为:②③④⑤,
故选:D.
7.B
【分析】
本题主要考查了平行线的性质与判定,如图所示,过点A作,过点B作,则,由得到,则,进而得到,再根据平行线的性质得到,由此即可得到.正确作出辅助线是解题的关键.
【详解】解:如图所示,过点A作,过点B作,
∵,
∴,
∵,
∴,即,
∵,
∴,
∴,
∵,,
∴,
∴,
∴,
故选:B.
8.D
【分析】
本题考查了平行线的性质,三角板中角度的求解,先根据平角的定义求出的度数,再利用两直线平行同位角相等即可求解.
【详解】解:如图,
,
,
,
故选:D.
9.D
【分析】分情况讨论:①与在的两侧,分别表示出与,然后根据内错角相等两直线平行,列式计算即可得解;②旋转到与都在的右侧,分别表示出与,然后根据同位角相等两直线平行,列式计算即可得解;③旋转到与都在的左侧,分别表示出与,然后根据同位角相等两直线平行,列式计算即可得解.
【详解】解:分三种情况:
如图①,与在的两侧时,
∵,,
∴,,
要使,则,
即,
解得;
此时,
∴;
②旋转到与都在的右侧时,
∵,,
要使,则,
即,
解得,
此时,
∴;
③旋转到与都在的左侧时,
∴,,
要使,则,
即,
解得,
此时,
而,
∴此情况不存在.
综上所述,当时间t的值为4秒或40秒时,与平行.
故选:D.
【点睛】本题考查了平行线的判定,读懂题意并熟练掌握平行线的判定方法是解题的关键,要注意分情况讨论.
10.A
【分析】先添加辅助线,再根据平行线的性质和三角形外角性质,求出与的关系式,最后由,即可求出范围,得出答案.
【详解】如图,延长,分别交和于点,,
∵,,
∴,
∵,
∴,
∵,,,
∴,
∴,
∴,整理得:,
∴,
解得:,
∴的最大整数值是.
故选:.
【点睛】本题考查了平行线的性质,三角形外角性质的应用,解题的关键是熟练掌握平行线的性质及等角度的转换.
11.
【分析】
本题主要考查了平行线的性质,两直线平行,同旁内角互补.正确作出辅助线是解题的关键.过B作,则.根据平行线的性质即可求解.
【详解】
解:过B作,
∵,
∴,
∴,
又∵,
∴,
∴,
∴.
故答案为:.
12./度;
【分析】
本题考查平行线的性质,根据两直线平行同位角相等即可得到答案;
【详解】解:∵,,
∴,
故答案为:.
13.59
【分析】
本题考查了直线平行的性质:两直线平行,同位角相等.也考查了对顶角的性质.根据两直线平行,同位角相等得到,再根据对顶角相等得,从而求出的度数.
【详解】解:,
,
,,
,
故答案为:59.
14./
【分析】
本题考查平行线的性质,根据两直线平行内错角相等即可得到答案;
【详解】解:过作,
由题意可得,
,
∵,
∴,
∴,,
∵,,
∴,
故答案为:.
15.
【分析】
本题考查了平行线的判定和性质,熟练掌握“平行于同一条直线的两直线平行”是解题的关键.
过点作,根据平行于同一条直线的两直线平行可得,根据两直线平行,内错角相等可得,求得,根据两直线平行,同旁内角互补即可求解.
【详解】解:如图:过点作,则,
∵,,
∴,
则,
∵,
∴;
故答案为:.
16.15
【分析】
本题主要考查了平行线的性质、角的和差等知识点,掌握两直线平行、内错角相等成为解题的关键.
由邻补角的定义可得,根据,然后根据角的和差即可解答.
【详解】解:∵,
∴,
∵,
∴,
∴.
故答案为:15.
17./100度
【分析】本题考查平行线的判定和性质.解题的关键是过拐点构造平行线.过点作,过点作,根据平行线的性质分别求出,,进而可求出的度数.
【详解】解:过点作,过点作,
∴,
∵,
∴.
∵ ,,,
∴,,
∵,
∴,
∴,
∴,
故答案为:.
18./度
【分析】过作,过作,可得,,,,,即可求解.
【详解】解:如图,过作,过作,
,
,
,,
,,
设,,
,,
和分别平分和,
, ,
,,
,
,
,
,
解得:,
;
故答案:.
【点睛】本题考查了平行线的性质,掌握性质,作出适当的辅助线是解题的关键.
19.
【分析】
本题主要考查平等线的判定与性质,由得出,由得,从而可得答案.
【详解】解:∵,
∴,
∴,
∵,
∴.
20.见解析
【分析】
本题考查了平行线的判定,掌握“同位角相等,两直线平行”是解题的关键.根据角平分线的定义结合对顶角得到,则可证明,根据平行线的判定即可证明.
【详解】
证明:因为平分,
所以.
因为,
所以.
因为,
所以.
所以.
21.,
【分析】
本题考查了平行线的判定和性质,邻补角的性质,掌握平行线的判定和性质是解题的关键.
根据证明,再利用平行线的性质求解即可.
【详解】解:∵,
∴,
∴,
∴.
22.(1)
(2)见解析
【分析】
本题主要考查了平行线的性质与判定,角平分线的定义,熟知平行线的性质与判定条件是解题的关键.
(1)由可得,进而可得的度数;
(2)由可得,结合平分,可得,再由平行线的判定,即可得出结论.
【详解】(1)解:∵,
∴,
∵,
∴.
(2)解:∵,
∴,
∴,
∵平分,
∴,
∴,
∴.
23.(1)
(2)不是最准确的
【分析】
本题考查的是平行线的性质,平行公理的应用,熟记两直线平行,同旁内角互补是解本题的关键.
(1)由,可得,根据可得;
(2)证明,可得,从而可得结论.
【详解】(1)解:,
.
,
.
,
;
(2)解:,,
.
.
.
,
此次瞄准不是最准确的.
24.(1)①;②图见解析,
(2)或
【分析】本题考查平行线的性质,解答时需要一定的灵活变换图形的能力,以及探究能力.
(1)①根据,,由两直线平行,同位角相等即可得到,利用等量代换即可得到,即可得出结论;②根据,,画出与射线延伸方向相反的情况,即可探究出α与β的另一种数量关系,再利用平行线的性质说明理由即可;
(2)根据题意,画出符合题意的两个图形,再利用平行线的性质探究出结论即可.
【详解】(1)解:①∵,
∴,
∵,
∴,
∴,
故答案为:;
②α与β的数量关系还可能是:.
图形如下:
理由如下:
∵,
∴,
∵,
∴,即;
(2)解:设的垂足为D.
情况1:如图,
∵,,
∴,
∵,
∴,即,
;
情况2:如图,
反向延长得,
由情况1,知,
∵,
∴,
整理,得,
,
综上,的值为:或.
25.(1)60
(2)A灯旋转30秒或110秒时,两灯的光束互相平行
(3)60或140或100
【分析】
本题主要考查了平行线的性质以及角的和差关系的运用,解决问题的关键是运用分类思想进行求解,解题时注意:两直线平行,内错角相等;两直线平行,同旁内角互补.
(1)根据,,即可得到的度数;
(2)设A灯转动t秒,两灯的光束互相平行,分两种情况进行讨论∶当时,根据,可得;当时,根据,可得;
(3)分两种情形,根据平行线的性质,构建方程解决问题即可.
【详解】(1)解:,,
.
故答案为:.
(2)设A灯转动t秒.两灯的光束互相平行,
①当时,如图1
,
,
,
,
,
,
解得:;
②当时,如图2,
,
,
,
,
解得:,
综上所述,A灯旋转30秒或110秒时.两灯的光束互相平行.
(3)设灯A射线转动时间为t秒,
,
,
又,
,
解得:(舍去)
或,
解得,
如图4中,当时
,
,
综上所述:满足条件的值为60或140或100秒.
故答案为:60或140或100.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第8章 角
- 8.1 角的表示
- 8.2 角的比较
- 8.3 角的度量
- 8.4 对顶角
- 8.5 垂直
- 第9章 平行线
- 9.1 同位角、内错角、同旁内角
- 9.2 平行线和它的画法
- 9.3 平行线的性质
- 9.4 平行线的判定
- 第10章 一次方程组
- 10.1 认识二元一次方程组
- 10.2 二元一次方程组的解法
- 10.3 三元一次方程组
- 10.4 列方程组解应用题
- 第11章 整式的乘除
- 11.1 同底数幂的乘法
- 11.2 积的乘方与幂的乘方
- 11.3 单项式的乘法
- 11.4 多项式乘多项式
- 11.5 同底数幂的除法
- 11.6 零指数幂与负整数指数幂
- 第12章 乘法公式与因式分解
- 12.1 平方差公式
- 12.2 完全平方公式
- 12.3 用提公因式法进行因式分解
- 12.4 用公式法进行因式分解
- 第13章 平面图形的认识
- 13.1 三角形
- 13.2 多边形
- 13.3 圆
- 第14章 位置与坐标
- 14.1 用有序数对表示位置
- 14.2 平面直角坐标系
- 14.3 直角坐标系中的图形
- 14.4 用方向和距离描述两个物体的相对位置
