人教版七年级下册9.3一元一次不等式组 课件(共22张PPT)
文档属性
| 名称 | 人教版七年级下册9.3一元一次不等式组 课件(共22张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 729.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-29 00:00:00 | ||
图片预览








文档简介
(共22张PPT)
一元一次不等式组
(第一课时)
人教版七年级下册
解下列不等式,并在数轴上表示解集:
一、复习巩固
学校在举办的《铸牢中华民族共同体意识》系列活动中需成立雪莲花合唱团,要在各班选拔学生(男女均可),但被选拔的同学应具备下列条件:
(1)身高x要高于160cm,(2)身高x要低于170cm.
请你列出我班两次都站起来的同学满足的不等关系式
x>160和x<170
这两个不等式同时成立。
二、一元一次不等式组的概念及解集
类似于方程组,由几个含同一未知数的一元一次不等式合起来,组成一个一元一次不等式组。
为此,我们用大括号把上述两个不等式联立起来,得
x>160和x<170
判断下列各式是不是一元一次不等式组?
í
ì
-
>
<
í
ì
>
+
<
-
2
1
)
2
(
1
3
3
6
7
2
)
1
(
x
x2
x
y
×
×
×
√
练一练
√
×
√
强调:
1.未知数的个数为1。
(一元)
2.未知数项的次数为1。
(一次)
3.由几个一元一次不等式组成。
4.必须是整式。
5.化简后是一元一次不等式。
对于不等式组 怎样确定不等式组中x取值范围呢?
一般地,几个不等式的解集的公共部分,叫做由它们所组成的一元一次不等式组的解集。
解不等式组就是求一元一次不等式组的解集的过程。
类比二元一次方程组的解和解二元一次方程组的概念,你能得出一元一次不等式组的解集和解一元一次不等式组的概念吗?
三、一元一次不等式组的解法
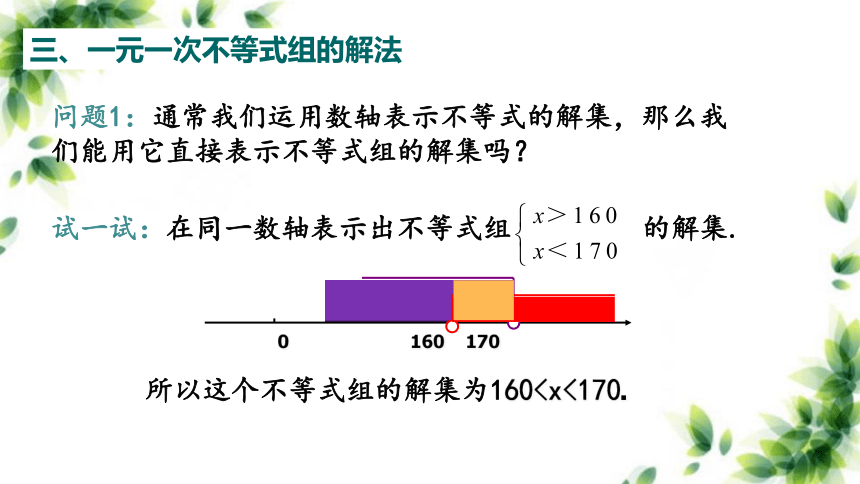
问题1:通常我们运用数轴表示不等式的解集,那么我们能用它直接表示不等式组的解集吗?
试一试:在同一数轴表示出不等式组 的解集.
所以这个不等式组的解集为1600 160 170
问题2:解由两个一元一次不等式组成的不等式组,在取各不等式的解的公共部分时,有几种不同情况
同大取大
问题2:解由两个一元一次不等式组成的不等式组,在取各不等式的解的公共部分时,有几种不同情况
同小取小
问题2:解由两个一元一次不等式组成的不等式组,在取各不等式的解的公共部分时,有几种不同情况
大小小大中间找
问题2:解由两个一元一次不等式组成的不等式组,在取各不等式的解的公共部分时,有几种不同情况
无解
无解
无解
无解
大大小小解不了
问题2:解由两个一元一次不等式组成的不等式组,在取各不等式的解的公共部分时,有几种不同情况
一元一次不等式组的解集图析(a>b)
填表:
不等式组
不等式组的 解集
x﹥-3
-5﹤x≤-3
x<-3
无解
练一练
例1.解下列不等式组:
(1) (2)
①
②
①
②
解:解不等式①,得 x>2
解不等式②,得 x>3
把不等式①②的解集在数轴上表示出来,如图所示
∴ 此不等式组的解集是x>3.
∴ 此不等式组无解.
(2)
①
②
∴ 此不等式组无解.
总结解一元一次不等式组的步骤:
(1)依次解各个一元一次不等式;
(2)把各个一元一次不等式的解集分别表示在同一条数轴上;
(3)根据解集在数轴上的表示的公共部分确定不等式组的解集。
(1) (2)
解:解不等式①,得 x>-2.4
解不等式②,得 x≤3.5
把不等式①②的解集在数轴上表示出来
∴ 此不等式组的解集是 -2.4<x≤3.5
解下列不等式组:
练一练
解: 解不等式①,得x ≤ 3.
0
-3
3
解不等式②,得x <-3.
把不等式①、②的解集在数轴上表示出来
∴此不等式组的解集是 x<-3.
①
②
非负整数时,
∴ x可取的整数值是0,1,2,3,4.
四、能力提升
解不等式3≤2X-1≤5 ,你觉得该怎样思考这个问题,你有解决的办法吗?
通过本节课学习,
你有哪些收获?
你学会了那些思考问题的方法?
你的兴奋点是...
五、课堂小结
必做题
1.数学书129页练习第1题
2.数学书130页习题9.3复习巩固第1.2题
能力提升
数学书130页习题9.3拓广探索第5题
六、作业布置
七、板书设计
一元一次不等式组
一、概念 二、一元一次不等式组的解法 例1 例2
1、定义 口诀
2、解集
3、解一元一次不等式组
一元一次不等式组
(第一课时)
人教版七年级下册
解下列不等式,并在数轴上表示解集:
一、复习巩固
学校在举办的《铸牢中华民族共同体意识》系列活动中需成立雪莲花合唱团,要在各班选拔学生(男女均可),但被选拔的同学应具备下列条件:
(1)身高x要高于160cm,(2)身高x要低于170cm.
请你列出我班两次都站起来的同学满足的不等关系式
x>160和x<170
这两个不等式同时成立。
二、一元一次不等式组的概念及解集
类似于方程组,由几个含同一未知数的一元一次不等式合起来,组成一个一元一次不等式组。
为此,我们用大括号把上述两个不等式联立起来,得
x>160和x<170
判断下列各式是不是一元一次不等式组?
í
ì
-
>
<
í
ì
>
+
<
-
2
1
)
2
(
1
3
3
6
7
2
)
1
(
x
x2
x
y
×
×
×
√
练一练
√
×
√
强调:
1.未知数的个数为1。
(一元)
2.未知数项的次数为1。
(一次)
3.由几个一元一次不等式组成。
4.必须是整式。
5.化简后是一元一次不等式。
对于不等式组 怎样确定不等式组中x取值范围呢?
一般地,几个不等式的解集的公共部分,叫做由它们所组成的一元一次不等式组的解集。
解不等式组就是求一元一次不等式组的解集的过程。
类比二元一次方程组的解和解二元一次方程组的概念,你能得出一元一次不等式组的解集和解一元一次不等式组的概念吗?
三、一元一次不等式组的解法
问题1:通常我们运用数轴表示不等式的解集,那么我们能用它直接表示不等式组的解集吗?
试一试:在同一数轴表示出不等式组 的解集.
所以这个不等式组的解集为160
问题2:解由两个一元一次不等式组成的不等式组,在取各不等式的解的公共部分时,有几种不同情况
同大取大
问题2:解由两个一元一次不等式组成的不等式组,在取各不等式的解的公共部分时,有几种不同情况
同小取小
问题2:解由两个一元一次不等式组成的不等式组,在取各不等式的解的公共部分时,有几种不同情况
大小小大中间找
问题2:解由两个一元一次不等式组成的不等式组,在取各不等式的解的公共部分时,有几种不同情况
无解
无解
无解
无解
大大小小解不了
问题2:解由两个一元一次不等式组成的不等式组,在取各不等式的解的公共部分时,有几种不同情况
一元一次不等式组的解集图析(a>b)
填表:
不等式组
不等式组的 解集
x﹥-3
-5﹤x≤-3
x<-3
无解
练一练
例1.解下列不等式组:
(1) (2)
①
②
①
②
解:解不等式①,得 x>2
解不等式②,得 x>3
把不等式①②的解集在数轴上表示出来,如图所示
∴ 此不等式组的解集是x>3.
∴ 此不等式组无解.
(2)
①
②
∴ 此不等式组无解.
总结解一元一次不等式组的步骤:
(1)依次解各个一元一次不等式;
(2)把各个一元一次不等式的解集分别表示在同一条数轴上;
(3)根据解集在数轴上的表示的公共部分确定不等式组的解集。
(1) (2)
解:解不等式①,得 x>-2.4
解不等式②,得 x≤3.5
把不等式①②的解集在数轴上表示出来
∴ 此不等式组的解集是 -2.4<x≤3.5
解下列不等式组:
练一练
解: 解不等式①,得x ≤ 3.
0
-3
3
解不等式②,得x <-3.
把不等式①、②的解集在数轴上表示出来
∴此不等式组的解集是 x<-3.
①
②
非负整数时,
∴ x可取的整数值是0,1,2,3,4.
四、能力提升
解不等式3≤2X-1≤5 ,你觉得该怎样思考这个问题,你有解决的办法吗?
通过本节课学习,
你有哪些收获?
你学会了那些思考问题的方法?
你的兴奋点是...
五、课堂小结
必做题
1.数学书129页练习第1题
2.数学书130页习题9.3复习巩固第1.2题
能力提升
数学书130页习题9.3拓广探索第5题
六、作业布置
七、板书设计
一元一次不等式组
一、概念 二、一元一次不等式组的解法 例1 例2
1、定义 口诀
2、解集
3、解一元一次不等式组
