【备课参考】2015秋冀教版数学八上课件17.5反证法(共24张PPT)
文档属性
| 名称 | 【备课参考】2015秋冀教版数学八上课件17.5反证法(共24张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 857.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-10-02 00:00:00 | ||
图片预览




文档简介
课件24张PPT。间接证明综合法 利用已知条件和某些数学定义、定理、
公理等,经过一系列的推理论证,最后推导
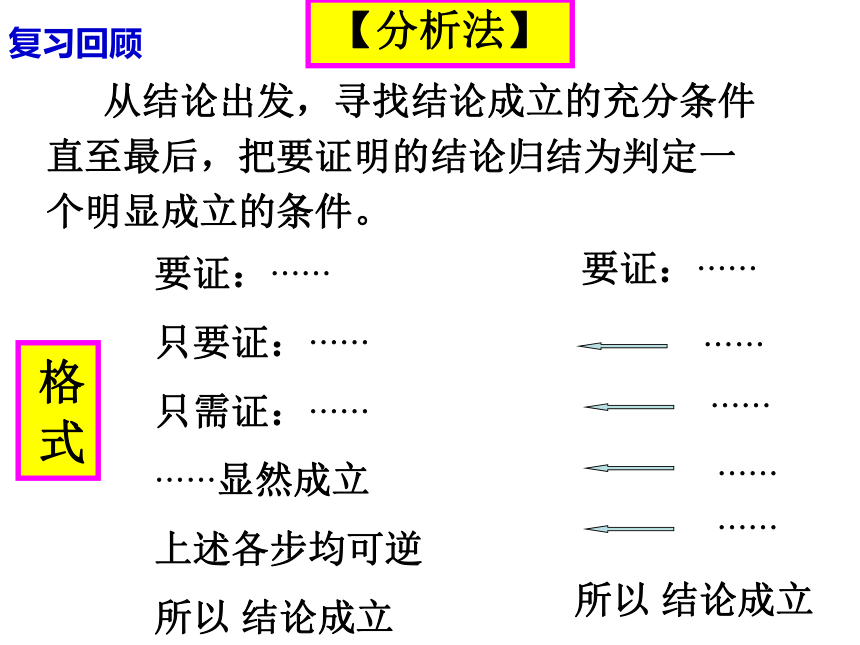
出所要证明的结论或所要解决的问题的结果。由因导果复习回顾【分析法】 从结论出发,寻找结论成立的充分条件
直至最后,把要证明的结论归结为判定一
个明显成立的条件。要证:??
只要证:??
只需证:??
??显然成立
上述各步均可逆
所以 结论成立格 式复习回顾
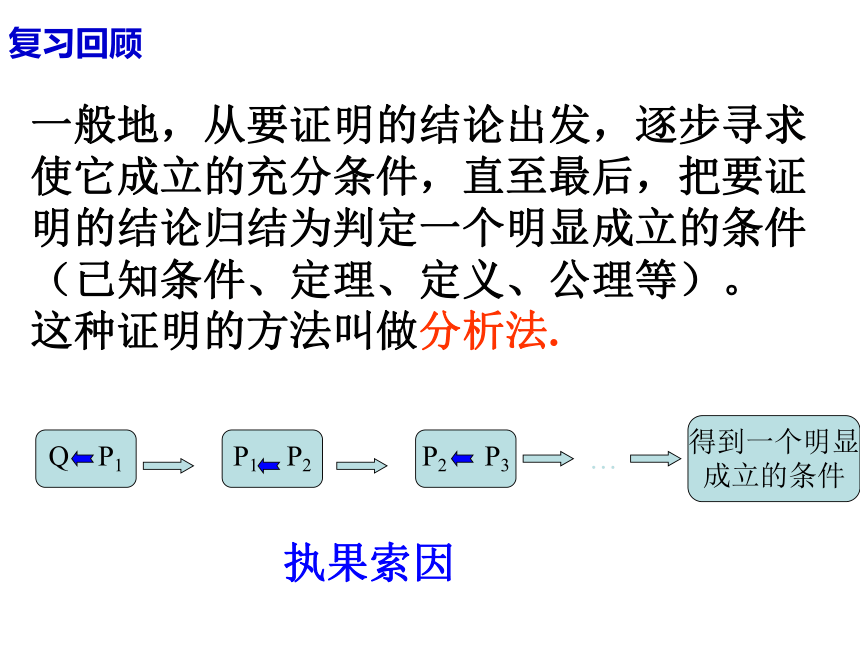
一般地,从要证明的结论出发,逐步寻求
使它成立的充分条件,直至最后,把要证
明的结论归结为判定一个明显成立的条件
(已知条件、定理、定义、公理等)。
这种证明的方法叫做分析法.Q P1P1 P2P2 P3得到一个明显
成立的条件…执果索因复习回顾1.直接证明的方法:(1)比较法:作差比较法;作商比较法;(2)综合法:(3)分析法:2.没有特别要求的证明题:
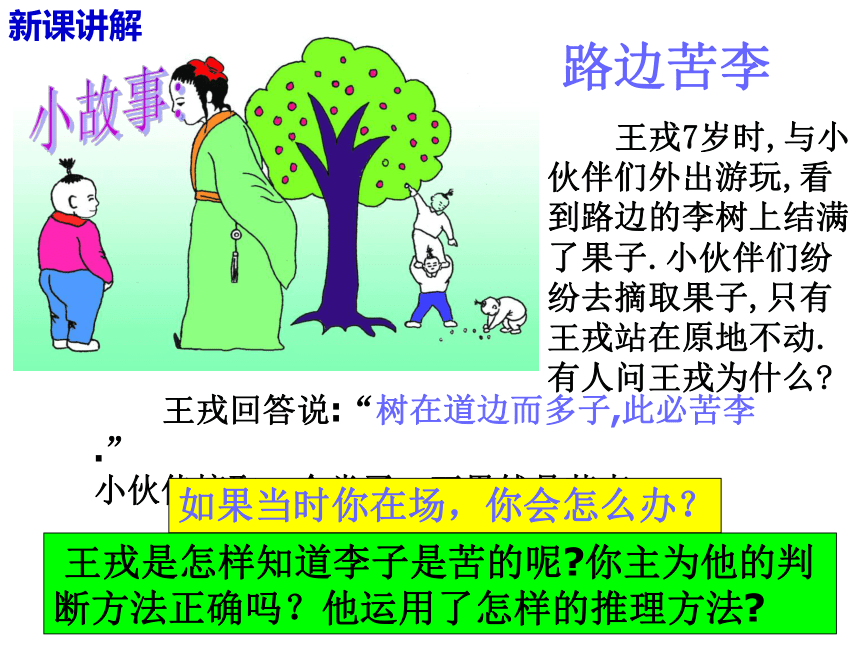
用分析法寻找证明思路,用综合法写出证明过程!路边苦李 王戎7岁时,与小伙伴们外出游玩,看到路边的李树上结满了果子.小伙伴们纷纷去摘取果子,只有王戎站在原地不动.有人问王戎为什么?
王戎回答说:“树在道边而多子,此必苦李.”
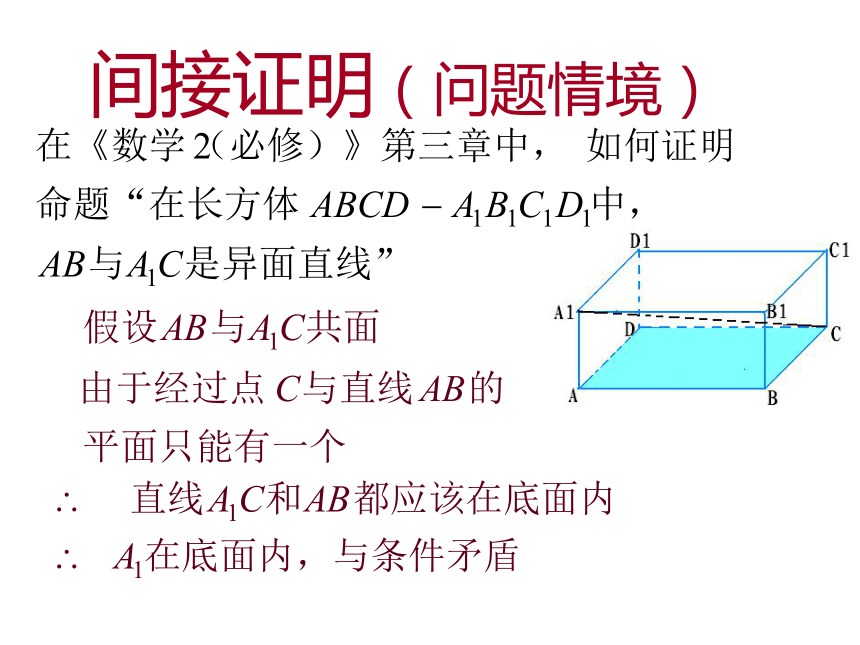
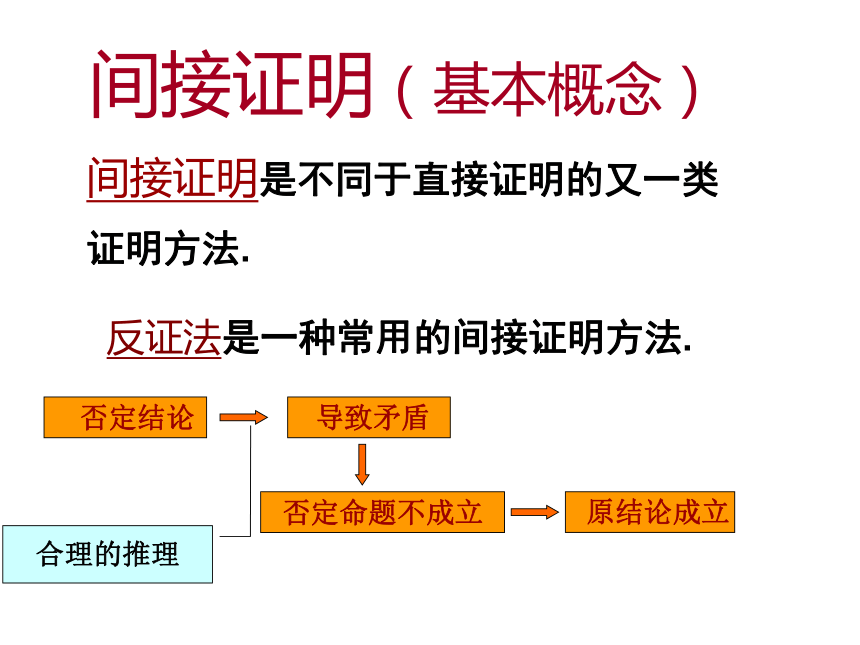
小伙伴摘取一个尝了一下果然是苦李. 王戎是怎样知道李子是苦的呢?你主为他的判断方法正确吗?他运用了怎样的推理方法?小故事:如果当时你在场,你会怎么办?新课讲解间接证明(问题情境)间接证明(基本概念)间接证明是不同于直接证明的又一类
证明方法.反证法是一种常用的间接证明方法. 否定结论 导致矛盾 否定命题不成立 原结论成立 合理的推理 在证明一个命题时,先假设命题不成立,
从这样的假设出发,经过推理得出和已知条件矛盾,或者与定义、公理、定理等矛盾,
从而得出假设命题不成立是错误的,
即所求证的命题正确.这种证明方法叫做反证法.反证法定义:例题1:求证在同一平面内,如果一条直线和两条平
行直线中的一条相交,那么和另一条也相交.已知:直线l1,l2,l3在同一平面内,且l1∥l2,l3与l1相交于点P.求证:l3与l2相交.l1l2l3Pl3与l2 不相交.l3∥l2l1∥l2 经过直线外一点,有且只有一条直线与已知直线平行假设推理矛盾假设不成立命题成立反证法的步骤一、提出假设二、推理论证三、得出矛盾四、结论成立以假设为条件,结合已知条件推理,得出与已知条件或是正确命题相矛盾的结论这与“......”相矛盾所以假设不成立,所求证的命题成立假设待证命题不成立,或是命题的反面成立。[能力测试]写出下列各结论的反面:
(1)a//b;
(2)a≥0;
(3)b是正数;
(4)a⊥ba<0b是0或负数a不垂直于b1.用反证法证明(填空):
在三角形的内角中,至少有一个角不小于60°已知:如图, ∠A,∠B,∠C是△ABC的内角求证: ∠A,∠B,∠C中至少有一个角不小于600.证明:假设所求证的结论不成立,即
∠A__60°, ∠B__60°, ∠C__60°
则 ∠A+∠B+∠C < 1800
这于_______________矛盾
所以假设______,
所以,所求证的结论成立.<<<三角形三个内角的和等于180°不成立2.已知:如图,直线l1,l2,l3在同一平面内,且l1∥l2,l3 ∥l1,l3∥l2求证:而l1∥l2,l3 ∥l1这与“经过直线外一点有且只有一条直线与已知直线
平行”相矛盾,所以假设不成立,即l3∥l2证明:假设T是正弦函数的周期则对任意实数x都有:令x=0,得即从而对任意实数x都应有这与矛盾.因此,原命题成立.解:例题2:先求出周期 思路 用反证法证明 是最小正周期.例题2:求证:若一个整数的平方是偶数,则这个数也是偶数.假设这个数是奇数,可以设为2k+1,证:则有而不是偶数这与原命题条件矛盾.例题3:练习:3.已知0(1-c)a, 不能都大于1/4证:假设(1-a)b,(1-b)c,(1-c)a都大于1/4,由(1-a)b>1/4和a>0得:由另两式得:b(1-c)a, 不能都大于1/4用反证法证题时,应注意的事项 :
??(1)周密考察原命题结论的否定事项,
防止否定不当或有所遗漏;
(2)推理过程必须完整,否则不能说
明命题的真伪性;
(3)在推理过程中,要充分使用已知条
件,否则推不出矛盾,或者不能断
定推出的结果是错误的。
间接证明(回顾小结)间接证明 反证法 同一法 枚举法 完全归纳法 间接证明(例题2)2.已知:求证:(2)中至少有一个不小于.(1)
公理等,经过一系列的推理论证,最后推导
出所要证明的结论或所要解决的问题的结果。由因导果复习回顾【分析法】 从结论出发,寻找结论成立的充分条件
直至最后,把要证明的结论归结为判定一
个明显成立的条件。要证:??
只要证:??
只需证:??
??显然成立
上述各步均可逆
所以 结论成立格 式复习回顾
一般地,从要证明的结论出发,逐步寻求
使它成立的充分条件,直至最后,把要证
明的结论归结为判定一个明显成立的条件
(已知条件、定理、定义、公理等)。
这种证明的方法叫做分析法.Q P1P1 P2P2 P3得到一个明显
成立的条件…执果索因复习回顾1.直接证明的方法:(1)比较法:作差比较法;作商比较法;(2)综合法:(3)分析法:2.没有特别要求的证明题:
用分析法寻找证明思路,用综合法写出证明过程!路边苦李 王戎7岁时,与小伙伴们外出游玩,看到路边的李树上结满了果子.小伙伴们纷纷去摘取果子,只有王戎站在原地不动.有人问王戎为什么?
王戎回答说:“树在道边而多子,此必苦李.”
小伙伴摘取一个尝了一下果然是苦李. 王戎是怎样知道李子是苦的呢?你主为他的判断方法正确吗?他运用了怎样的推理方法?小故事:如果当时你在场,你会怎么办?新课讲解间接证明(问题情境)间接证明(基本概念)间接证明是不同于直接证明的又一类
证明方法.反证法是一种常用的间接证明方法. 否定结论 导致矛盾 否定命题不成立 原结论成立 合理的推理 在证明一个命题时,先假设命题不成立,
从这样的假设出发,经过推理得出和已知条件矛盾,或者与定义、公理、定理等矛盾,
从而得出假设命题不成立是错误的,
即所求证的命题正确.这种证明方法叫做反证法.反证法定义:例题1:求证在同一平面内,如果一条直线和两条平
行直线中的一条相交,那么和另一条也相交.已知:直线l1,l2,l3在同一平面内,且l1∥l2,l3与l1相交于点P.求证:l3与l2相交.l1l2l3Pl3与l2 不相交.l3∥l2l1∥l2 经过直线外一点,有且只有一条直线与已知直线平行假设推理矛盾假设不成立命题成立反证法的步骤一、提出假设二、推理论证三、得出矛盾四、结论成立以假设为条件,结合已知条件推理,得出与已知条件或是正确命题相矛盾的结论这与“......”相矛盾所以假设不成立,所求证的命题成立假设待证命题不成立,或是命题的反面成立。[能力测试]写出下列各结论的反面:
(1)a//b;
(2)a≥0;
(3)b是正数;
(4)a⊥ba<0b是0或负数a不垂直于b1.用反证法证明(填空):
在三角形的内角中,至少有一个角不小于60°已知:如图, ∠A,∠B,∠C是△ABC的内角求证: ∠A,∠B,∠C中至少有一个角不小于600.证明:假设所求证的结论不成立,即
∠A__60°, ∠B__60°, ∠C__60°
则 ∠A+∠B+∠C < 1800
这于_______________矛盾
所以假设______,
所以,所求证的结论成立.<<<三角形三个内角的和等于180°不成立2.已知:如图,直线l1,l2,l3在同一平面内,且l1∥l2,l3 ∥l1,l3∥l2求证:而l1∥l2,l3 ∥l1这与“经过直线外一点有且只有一条直线与已知直线
平行”相矛盾,所以假设不成立,即l3∥l2证明:假设T是正弦函数的周期则对任意实数x都有:令x=0,得即从而对任意实数x都应有这与矛盾.因此,原命题成立.解:例题2:先求出周期 思路 用反证法证明 是最小正周期.例题2:求证:若一个整数的平方是偶数,则这个数也是偶数.假设这个数是奇数,可以设为2k+1,证:则有而不是偶数这与原命题条件矛盾.例题3:练习:3.已知0
??(1)周密考察原命题结论的否定事项,
防止否定不当或有所遗漏;
(2)推理过程必须完整,否则不能说
明命题的真伪性;
(3)在推理过程中,要充分使用已知条
件,否则推不出矛盾,或者不能断
定推出的结果是错误的。
间接证明(回顾小结)间接证明 反证法 同一法 枚举法 完全归纳法 间接证明(例题2)2.已知:求证:(2)中至少有一个不小于.(1)
同课章节目录
- 第十二章 分式和分式方程
- 12.1 分式
- 12.2 分式的乘除
- 12.3 分式的加减
- 12.4 分式方程
- 12.5 分式方程的应用
- 第十三章 全等三角形
- 13.1 命题与证明
- 13.2 全等图形
- 13.3 全等三角形的判定
- 13.4 三角形的尺规作图
- 第十四章 实数
- 14.1 平方根
- 14.2 立方根
- 14.3 实数
- 14.4 近似数
- 14.5 用计算器求平方根与立方根
- 第十五章 二次根式
- 15.1 二次根式
- 15.2 二次根式的乘除
- 15.3 二次根式的加减
- 15.4 二次根式的混合
- 第十六章 轴对称和中心对称
- 16.1 轴对称
- 16.2 线段的垂直平分
- 16.3 角的平分线
- 16.4 中心对称图形
- 16.5 利用图形的平移、旋转和轴对称设计图案
- 第十七章 特殊三角形
- 17.1 等腰三角形
- 17.2 直角三角形
- 17.3 勾股定理
- 17.4 直角三角形全等的判定
- 17.5 反证法
