第八章 8.3.2 圆柱、圆锥、圆台、球的表面积和体积 课件(共29张PPT)
文档属性
| 名称 | 第八章 8.3.2 圆柱、圆锥、圆台、球的表面积和体积 课件(共29张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-31 00:00:00 | ||
图片预览






文档简介
(共29张PPT)
第七章
8.3.2 圆柱、圆锥、圆台、球的表面积和体积
人教A版(2019)
教学目标
学习目标 数学素养
1.了解圆柱、圆锥、圆台、球的表面积和体积计算公式. 1.数学运算素养.
2.理解并掌握侧面展开图与几何体的表面积之间的关系,并能运用计算公式求几何体的表面积和体积. 2.数学抽象素养.
温故知新
矩形面积公式:
圆面积公式:
圆周长公式:
扇形面积公式:
棱柱、棱锥、棱台的表面积就是围成它们的各个面的面积的和,也就是展开图的面积.
s
知新探究
圆柱、圆锥、圆台的表面积
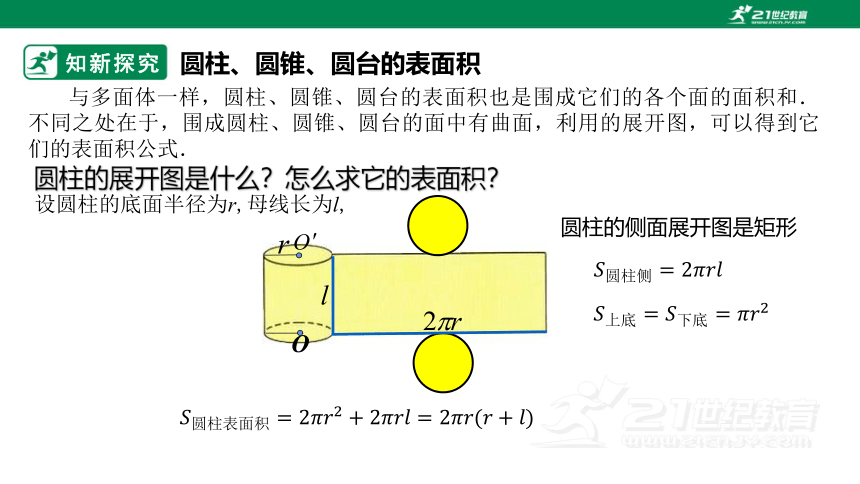
与多面体一样,圆柱、圆锥、圆台的表面积也是围成它们的各个面的面积和.不同之处在于,围成圆柱、圆锥、圆台的面中有曲面,利用的展开图,可以得到它们的表面积公式.
圆柱的展开图是什么?怎么求它的表面积?
设圆柱的底面半径为r,母线长为l,
圆柱的侧面展开图是矩形
O
知新探究
圆柱、圆锥、圆台的表面积
圆锥的展开图是什么?怎么求它的表面积?
设圆锥的底面半径为r,母线长为l,
O
圆锥的侧面展开图是扇形
如图中,.
.
知新探究
圆柱、圆锥、圆台的表面积
参照圆柱和圆锥的侧面展开图,试想象圆台的侧面展开图是什么 ,它的表面积是什么?
设r′、r分别是上、下底面半径,l是母线长,
).
O
O’
圆台的侧面展开图是扇环
知新探究
圆柱、圆锥、圆台的表面积
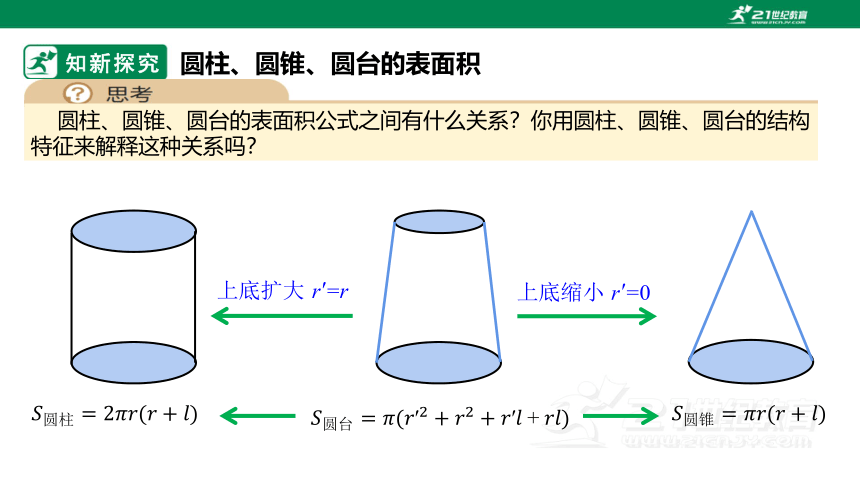
圆柱、圆锥、圆台的表面积公式之间有什么关系?你用圆柱、圆锥、圆台的结构特征来解释这种关系吗?
知新探究
圆柱、圆锥、圆台的表面积
知新探究
圆柱、圆锥、圆台的体积
我们以前学习圆柱、圆锥的体积公式,即
知新探究
圆柱、圆锥、圆台的体积
由于圆台是由圆锥截成的,因此可以利用圆锥的体积公式推导出圆台的体积公式
h
知新探究
圆柱、圆锥、圆台的体积
圆柱、圆锥、圆台的体积公式之间有什么关系?你用圆柱、圆锥、圆台的结构特征来解释这种关系吗?
知新探究
圆柱、圆锥、圆台的体积
结合棱柱、棱锥、棱台和圆柱、圆锥、圆台的体积公式,你将它们统一成柱体、锥体、台体的体积公式吗?
知新探究
柱体、锥体、台体的体积公式之间的关系
上底扩大
上底缩小
S为底面面积,h为柱体高
S分别为上、下底面面积,h 为台体高
S为底面面积,h为锥体高
知新探究
球的表面积和体积
设球的半径为R,它的表面积只与半径R有关,是以R为自变量的函数.
事实上,如果球的半径为R,那么它的表面积是
R
知新探究
球的表面积和体积
小学,我们学习了圆的面积公式,你还记得是如何求得的吗 类比这种方法你能由球的表面积公式推导出球的体积公式
类比利用圆的周长求圆的面积的方法,我们可以利用球的表面积求球的体积.如图,把球O的表面分成n个小网格,连接球心O和每个小网格的顶点,整个球体就被分割成n个“小锥形”.
O
A
B
D
C
O
A
B
C
D
知新探究
球的表面积和体积
当n越大,每个小网格越小时,每个“小锥体”的底面就越平,“小锥体”就越近似于棱锥,其高越近似于半径R.设O-ABCD是其中的一个“小锥体”,它的体积
O
A
B
D
C
O
A
B
C
D
.
由于球的体积就是n个“小锥体”的体积之和,而这n个“小锥体”的底面积之和就是球的表面积.因此,球的体积
.
由此,我们得到了球的体积公式
.
知新探究
球的表面积和体积
R
.
球的表面积、体积公式
设球的半径为R,
知新探究
【例1】如图,某种浮标由两个半球和一个圆柱黏合而成,半球的直径是0.3m,圆柱高0.6m.如果在浮标表面涂一层防水漆,每平方米需要0.5kg涂料,那么给1000个这样的浮标涂防水漆需要多少涂料?()
一个浮标的表面积为
解:
0.8478(m3)
所以给1000个这样的浮标涂防水漆需涂料
423.9(kg).
知新探究
【例2】如图,圆柱的底面直径和高都等于球的直径,求球与圆柱的体积之比.
解:
设球的半径为R,则圆柱的底面半径为R,高为2R,
∵,.
∴.
拓展:证明球的表面积等于圆柱的侧面积.
∵.
∴.
知新探究
【例3】如图,正方体的棱长为a,它的各个顶点都在球的球面上,求球的表面积和体积.
解:
由正方体内接于球得,球的直径等于正方体的对角线长.
∴,即.
∴.
拓展:如图,正方体的各个顶点都在球上(球内接正方体)若球的半径为R,求正方体的表面积和体积.
分析:正方体内接于球,则由球和正方体都是中心对称图形可知,它们中心重合,则正方体对角线与球的直径相等.
初试身手
1.⑴圆柱的一个底面积是S,侧面展开图是一个正方形,那么这个圆柱的侧面积为( )
A. B. C. D.
⑵圆台的上、下底面面积分别是π、4π,侧面积是6π,这个圆台的体积是 .
解:
⑴设圆柱底面半径为r,则,母线
∴,故选A.
A
⑵如图,设上底面半径为r,下底面半径为R,母线长为l,高为h.
∵,
∴
∴
则.
.
初试身手
2.在梯形ABCD中,∠ABC=,AD∥BC,BC=2AD=2AB=2.将梯形ABCD绕AD所在直线旋转一周而形成的曲面所围成的几何体的表面积为( )
A.4π B.(4+)π C.6π D.(5+)π
解:
∵在梯形ABCD中,∠ABC=,AD∥BC,BC=2AD=2AB=2,
∴将梯形ABCD绕AD所在直线旋转一周而形成的曲面所围成的几何体是一个底面半径为AB=1,高为BC=2的圆柱减去一个底面半径为AB=1,高为BC-AD=2-1=1的圆锥的组合体.
∴几何体的表面积
=.
D
初试身手
3.已知正四棱锥的顶点都在同一球面上,且该棱锥的高为4,底面边长为,则该球的体积为________.
解:
如图,设球的半径为R,则正四棱锥的高=4,
在Rt△A中,,
即
解得 .
而,=2,
球的体积.
.
课堂小结
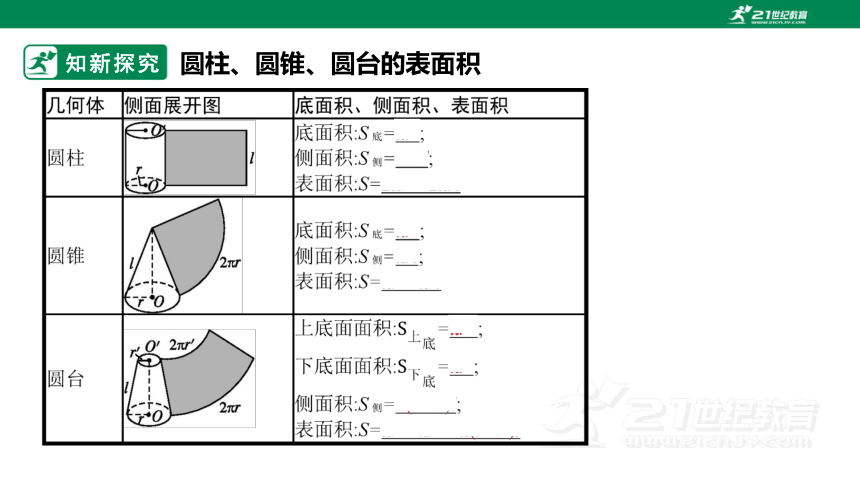
1.柱体、锥体、台体的表面积
圆台
圆柱
圆锥
2.柱体、锥体、台体的体积
柱体
台体
锥体
课堂小结
3.球的体积、表面积公式
R
.
设球的半径为R,
作业布置
作业: P120 习题8. 第4,5,7,8, 9题.
尽情享受学习数学的快乐吧!
我们下节课再见!
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
第七章
8.3.2 圆柱、圆锥、圆台、球的表面积和体积
人教A版(2019)
教学目标
学习目标 数学素养
1.了解圆柱、圆锥、圆台、球的表面积和体积计算公式. 1.数学运算素养.
2.理解并掌握侧面展开图与几何体的表面积之间的关系,并能运用计算公式求几何体的表面积和体积. 2.数学抽象素养.
温故知新
矩形面积公式:
圆面积公式:
圆周长公式:
扇形面积公式:
棱柱、棱锥、棱台的表面积就是围成它们的各个面的面积的和,也就是展开图的面积.
s
知新探究
圆柱、圆锥、圆台的表面积
与多面体一样,圆柱、圆锥、圆台的表面积也是围成它们的各个面的面积和.不同之处在于,围成圆柱、圆锥、圆台的面中有曲面,利用的展开图,可以得到它们的表面积公式.
圆柱的展开图是什么?怎么求它的表面积?
设圆柱的底面半径为r,母线长为l,
圆柱的侧面展开图是矩形
O
知新探究
圆柱、圆锥、圆台的表面积
圆锥的展开图是什么?怎么求它的表面积?
设圆锥的底面半径为r,母线长为l,
O
圆锥的侧面展开图是扇形
如图中,.
.
知新探究
圆柱、圆锥、圆台的表面积
参照圆柱和圆锥的侧面展开图,试想象圆台的侧面展开图是什么 ,它的表面积是什么?
设r′、r分别是上、下底面半径,l是母线长,
).
O
O’
圆台的侧面展开图是扇环
知新探究
圆柱、圆锥、圆台的表面积
圆柱、圆锥、圆台的表面积公式之间有什么关系?你用圆柱、圆锥、圆台的结构特征来解释这种关系吗?
知新探究
圆柱、圆锥、圆台的表面积
知新探究
圆柱、圆锥、圆台的体积
我们以前学习圆柱、圆锥的体积公式,即
知新探究
圆柱、圆锥、圆台的体积
由于圆台是由圆锥截成的,因此可以利用圆锥的体积公式推导出圆台的体积公式
h
知新探究
圆柱、圆锥、圆台的体积
圆柱、圆锥、圆台的体积公式之间有什么关系?你用圆柱、圆锥、圆台的结构特征来解释这种关系吗?
知新探究
圆柱、圆锥、圆台的体积
结合棱柱、棱锥、棱台和圆柱、圆锥、圆台的体积公式,你将它们统一成柱体、锥体、台体的体积公式吗?
知新探究
柱体、锥体、台体的体积公式之间的关系
上底扩大
上底缩小
S为底面面积,h为柱体高
S分别为上、下底面面积,h 为台体高
S为底面面积,h为锥体高
知新探究
球的表面积和体积
设球的半径为R,它的表面积只与半径R有关,是以R为自变量的函数.
事实上,如果球的半径为R,那么它的表面积是
R
知新探究
球的表面积和体积
小学,我们学习了圆的面积公式,你还记得是如何求得的吗 类比这种方法你能由球的表面积公式推导出球的体积公式
类比利用圆的周长求圆的面积的方法,我们可以利用球的表面积求球的体积.如图,把球O的表面分成n个小网格,连接球心O和每个小网格的顶点,整个球体就被分割成n个“小锥形”.
O
A
B
D
C
O
A
B
C
D
知新探究
球的表面积和体积
当n越大,每个小网格越小时,每个“小锥体”的底面就越平,“小锥体”就越近似于棱锥,其高越近似于半径R.设O-ABCD是其中的一个“小锥体”,它的体积
O
A
B
D
C
O
A
B
C
D
.
由于球的体积就是n个“小锥体”的体积之和,而这n个“小锥体”的底面积之和就是球的表面积.因此,球的体积
.
由此,我们得到了球的体积公式
.
知新探究
球的表面积和体积
R
.
球的表面积、体积公式
设球的半径为R,
知新探究
【例1】如图,某种浮标由两个半球和一个圆柱黏合而成,半球的直径是0.3m,圆柱高0.6m.如果在浮标表面涂一层防水漆,每平方米需要0.5kg涂料,那么给1000个这样的浮标涂防水漆需要多少涂料?()
一个浮标的表面积为
解:
0.8478(m3)
所以给1000个这样的浮标涂防水漆需涂料
423.9(kg).
知新探究
【例2】如图,圆柱的底面直径和高都等于球的直径,求球与圆柱的体积之比.
解:
设球的半径为R,则圆柱的底面半径为R,高为2R,
∵,.
∴.
拓展:证明球的表面积等于圆柱的侧面积.
∵.
∴.
知新探究
【例3】如图,正方体的棱长为a,它的各个顶点都在球的球面上,求球的表面积和体积.
解:
由正方体内接于球得,球的直径等于正方体的对角线长.
∴,即.
∴.
拓展:如图,正方体的各个顶点都在球上(球内接正方体)若球的半径为R,求正方体的表面积和体积.
分析:正方体内接于球,则由球和正方体都是中心对称图形可知,它们中心重合,则正方体对角线与球的直径相等.
初试身手
1.⑴圆柱的一个底面积是S,侧面展开图是一个正方形,那么这个圆柱的侧面积为( )
A. B. C. D.
⑵圆台的上、下底面面积分别是π、4π,侧面积是6π,这个圆台的体积是 .
解:
⑴设圆柱底面半径为r,则,母线
∴,故选A.
A
⑵如图,设上底面半径为r,下底面半径为R,母线长为l,高为h.
∵,
∴
∴
则.
.
初试身手
2.在梯形ABCD中,∠ABC=,AD∥BC,BC=2AD=2AB=2.将梯形ABCD绕AD所在直线旋转一周而形成的曲面所围成的几何体的表面积为( )
A.4π B.(4+)π C.6π D.(5+)π
解:
∵在梯形ABCD中,∠ABC=,AD∥BC,BC=2AD=2AB=2,
∴将梯形ABCD绕AD所在直线旋转一周而形成的曲面所围成的几何体是一个底面半径为AB=1,高为BC=2的圆柱减去一个底面半径为AB=1,高为BC-AD=2-1=1的圆锥的组合体.
∴几何体的表面积
=.
D
初试身手
3.已知正四棱锥的顶点都在同一球面上,且该棱锥的高为4,底面边长为,则该球的体积为________.
解:
如图,设球的半径为R,则正四棱锥的高=4,
在Rt△A中,,
即
解得 .
而,=2,
球的体积.
.
课堂小结
1.柱体、锥体、台体的表面积
圆台
圆柱
圆锥
2.柱体、锥体、台体的体积
柱体
台体
锥体
课堂小结
3.球的体积、表面积公式
R
.
设球的半径为R,
作业布置
作业: P120 习题8. 第4,5,7,8, 9题.
尽情享受学习数学的快乐吧!
我们下节课再见!
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
