第1课时 数列的概念与简单表示法
文档属性
| 名称 | 第1课时 数列的概念与简单表示法 |

|
|
| 格式 | pptx | ||
| 文件大小 | 10.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-01 00:00:00 | ||
图片预览











文档简介
(共52张PPT)
4.1数列的概念
第1课时 数列的概念与简单表示法
答辩人:亮亮图文
1.数列及其相关概念
(1)定义:按___________排列的一列数叫做数列.
(2)项:数列中的_________叫做这个数列的项.
(3)形式:a1,a2,a3,…,an,…,简记为{an},其中an是数列的第__项,第1项也叫做
首项.
确定的顺序
每一个数
n
【思考】
(1)如果组成两个数列的数相同但排列次序不同,那么它们是相同的数列吗
提示:从数列的定义可以看出,组成数列的数是按一定顺序排列的,如果组成数列的数相同但排列次序不同,那么它们就不是同一数列.
(2)同一个数在数列中可以重复出现吗
提示:在数列的定义中,并没有规定数列中的数必须不同,因此,同一个数在数列中可以重复出现.例如:1,-1,1,-1,1,…;2,2,2,….
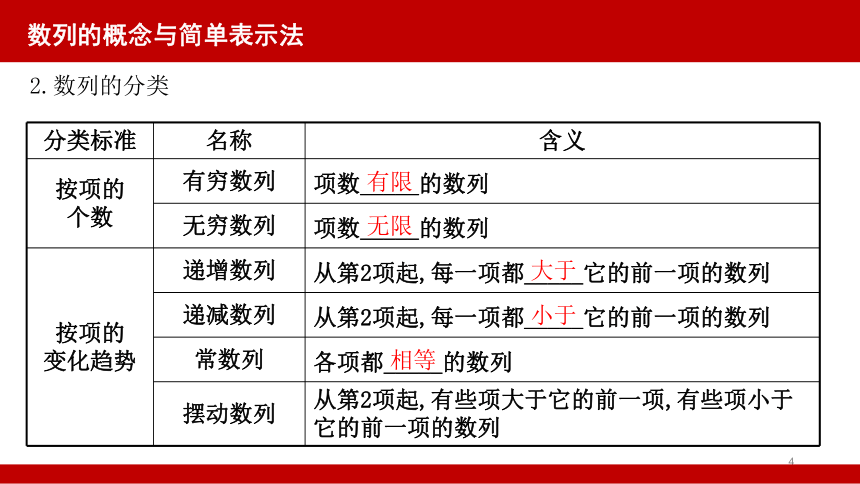
2.数列的分类
分类标准 名称 含义
按项的 个数 有穷数列 项数_____的数列
无穷数列 项数_____的数列
按项的 变化趋势 递增数列 从第2项起,每一项都_____它的前一项的数列
递减数列 从第2项起,每一项都_____它的前一项的数列
常数列 各项都_____的数列
摆动数列 从第2项起,有些项大于它的前一项,有些项小于它的前一项的数列
有限
无限
大于
小于
相等
3.函数与数列的关系
数列{an}是从________(或它的有限子集{1,2,…,n})到实数集R的函数,自变量
是序号n,对应的函数值是数列的第n项an,记为an=f(n).
正整数N*
4.数列的通项公式:如果数列{an}的第n项an与它的序号n之间的对应关系可以
用_________来表示,那么这个式子叫做这个数列的通项公式.
一个式子
1.思维辨析(对的打“√”,错的打“×”)
(1)1,2,3,4和1,2,4,3是相同的数列. ( )
(2){an}与an是一样的,都表示数列. ( )
(3)所有数列都能写出其通项公式且一个数列的通项公式是唯一的. ( )
(4)数列3,1,-1,-3,-5,-10的通项公式为an=5-2n.( )
提示:(1)×.两个数列相同,每一项都必须相同,而且数列具有顺序性.
(2)×.因为{an}代表一个数列,而an只是这个数列中的第n项,故{an}与an是不一样的.
(3)×.有的数列就没有通项公式,而且有的数列的通项公式不唯一.
(4)×. 第六项为-10,不符合an=5-2n,故an=5-2n不是此数列的通项公式.
2.数列3,4,5,6,…的一个通项公式为 ( )
A.an=n,n∈N* B.an=n+1,n∈N*
C.an=n+2,n∈N* D.an=2n,n∈N*
【解析】选C.这个数列的前4项都比序号大2,所以,它的一个通项公式为an=n+2,n∈N*.
3.已知数列{an}的通项公式是an=n2+1,则122是该数列的 ( )
A.第9项 B.第10项 C.第11项 D.第12项
【解析】选C.令n2+1=122,则n2=121,
所以n=11或n=-11(舍去).
4.已知数列{an}的通项公式是an=2n-1,则a8=________.
【解析】a8=2×8-1=15.
答案:15
题型一 数列的概念以及分类
【典例】1.下列说法错误的是 ( )
A.数列4,7,3,4的首项是4
B.数列{an}中,若a1=3,则从第2项起,各项均不等于3
C.数列1,2,3,…就是数列{n}
D.数列中的项不能是三角形
2.已知下列数列:
①2 011,2 012,2 013,2 014,2 015,2 016;
②1, , ,…, ,…;
③1,- , ,…, ,…;
④1,0,-1,…,sin ,…;
⑤2,4,8,16,32,…;
⑥-1,-1,-1,-1.
其中,有穷数列是________,无穷数列是________,递增数列是________,递减数列是________,常数列是________,摆动数列是________(填序号).
【思维·引】1.依据数列的定义逐项判断.
2.依据数列分类中有关数列的定义,逐个判断.
【解析】1.选B.由数列的相关概念可知,数列4,7,3,4的首项是4,故A正确.
同一个数在数列中可以重复出现,故B错误.
按一定顺序排列的一列数称为数列,所以数列1,2,3,…就是数列{n},故C正确.
数列中的项必须是数,不能是其他形式,故D正确.
2.①为有穷数列且为递增数列;②为无穷数列、递减数列;③为无穷数列、摆动数列;④是摆动数列,也是无穷数列;⑤为递增数列,也是无穷数列;⑥为有穷数列,也是常数列.
答案:①⑥ ②③④⑤ ①⑤ ② ⑥ ③④
【内化·悟】
1.与集合中元素的性质相比较,数列中的项的性质具有哪些特点
提示:(1)确定性:一个数是或不是某一数列中的项是确定的,集合中的元素也具有确定性;
(2)可重复性:数列中的数可以重复,而集合中的元素不能重复出现(即互异性);
(3)有序性:一个数列不仅与构成数列的“数”有关,而且与这些数的排列顺序有关,而集合中的元素没有顺序(即无序性);
(4)数列中的每一项都是数,而集合中的元素还可以代表除数字外的其他事物.
2.如何判断两个数列是相同数列
提示:组成数列的数相同,且排列次序也相同的两个数列才是相同的数列.
【类题·通】
数列概念的三个注意点
(1)数列{an}表示数列a1,a2,a3,…,an,…,不是表示一个集合,与集合表示有本质的区别.
(2)从数列的定义可以看出,如果组成数列的数相同而排列次序不同,那么它们就是不同的数列;在定义中,并没有规定数列中的数必须不同,因此,同一个数在数列中可以重复出现.
(3)数列中各项的次序揭示了数列的规律性,是理解、把握数列的关键.
【习练·破】
下列数列中,既是无穷数列又是递增数列的是 ( )
A.1, , ,…
B.sin ,sin ,sin ,sin ,…
C.-1,- ,- ,- ,…
D.1,2,3,4,…,30
【解析】选C.数列1, , ,…是无穷数列,但它不是递增数列,而是递减
数列;数列sin ,sin ,sin ,sin ,…是无穷数列,但它既不是递增数
列,又不是递减数列;数列-1,- ,- ,- ,…是无穷数列,也是递增数列;数列
1,2,3,4,…,30是递增数列,但不是无穷数列.
【加练·固】
下列数列
(1)1,2,22,23,…,263;
(2)0,10,20,30,…,1 000;
(3)2,4,6,8,10,…;
(4)-1,1,-1,1,-1,…;
(5)7,7,7,7,…;
(6)
其中有穷数列是________,无穷数列是________,递增数列是________,递减数列是________,摆动数列是________,常数列是________.(填序号)
【解析】根据数列的概念知有穷数列是(1)(2),无穷数列是 (3)(4)(5)(6),递增数列是(1)(2)(3),递减数列是(6),摆动数列是 (4),常数列是(5).
答案:(1)(2) (3)(4)(5)(6) (1)(2)(3) (6) (4) (5)
类型二 观察法写出数列的通项公式
【典例】1.(2020·徐州高一检测)数列3,6,11,20,…的一个通项公式为
( )
A.an=3n B.an=n(n+2)
C.an=n+2n D.an=2n+1
2.写出下列数列的一个通项公式:
(1) ,2, ,8, ,…;
(2)1,-3,5,-7,9,…;
(3)9,99,999,9 999,…;
(4) …;
(5) …;
(6)4,0,4,0,4,0,….
【思维·引】1.根据特点,观察、分析,寻找数列的每一项与其所在项的序号之间的关系,归纳出一个通项公式即可.
2.首先要熟悉一些常见数列的通项公式,然后对于复杂数列的通项公式,其项与序号之间的关系不容易发现,要将数列各项的结构形式加以变形,将数列的各项分解成若干个常见数列对应项的“和”“差”“积”“商”后再进行归纳.
【解析】1.选C.依题意,a1=3=1+21;a2=6=2+22;a3=11=3+23;a4=20=4+24;…,
所以an=n+2n.
2.(1)数列的项有的是分数,有的是整数,可先将各项都统一成分数再观察:
…,所以,它的一个通项公式为an= .
(2)数列各项的绝对值分别为1,3,5,7,9,…是连续的正奇数,其通项公式为2n
-1;考虑(-1)n+1具有转换符号的作用,所以数列的一个通项公式为an=(-1)n+1(2n
-1).
(3)各项加1后,分别变为10,100,1 000,10 000,…此数列的通项公式为10n,可
得原数列的一个通项公式为an=10n-1.
(4)数列中每一项均由三部分组成,分母是从1开始的奇数列,其通项公式为2n-
1;分子的前一部分是从2开始的自然数的平方,分子的后一部分是减去一个从1
开始的自然数,综合得原数列的一个通项公式为an=
(5)这个数列的前4项的绝对值都等于序号与序号加1的积的倒数,且奇数项为
负,偶数项为正,所以它的一个通项公式是an=(-1)n·
(6)由于该数列中,奇数项全部都是4,偶数项全部都是0,因此可用分段函数的
形式表示通项公式,即an=
又因为数列可改写为2+2,2-2,2+2,2-2,2+2,2-2,…,因此其通项公式又可表示
为an=2+2×(-1)n+1.
【素养·探】
在与观察法写出数列的通项公式有关的问题中,经常利用核心素养中的逻辑推理,通过研究数列的前几项与项的序号之间的关系,归纳出数列的通项公式.
将本例2(6)的数列改为“3,5,3,5,3,5,…”,如何写出其通项公式
【解析】此数列的奇数项为3,偶数项为5,故通项公式可写为an=
此数列两项3与5的平均数为 =4,
奇数项为4-1,偶数项为4+1,
故通项公式还可写为an=4+(-1)n.
【类题·通】
(1)用观察法求数列通项公式的策略
(2)对于符号交替出现的情况,可先观察其绝对值,再用(-1)k处理符号问题.
(3)对于周期出现的数列,可考虑拆成几个简单数列和的形式,或者利用周期函数,如三角函数等.
【习练·破】
写出下列数列的一个通项公式:
(1)0,3,8,15,24,…;
(2)1 ,2 ,3 ,4 ,…;
(3)1,11,111,1 111,….
【解析】(1)观察数列中的数,可以看到0=1-1,3=4-1,8=9-1,15=16-1,24=25-1,
…,所以它的一个通项公式是an=n2-1(n∈N*).
(2)此数列的整数部分1,2,3,4,…恰好是序号n,分数部分与序号n的关系为
故所求的数列的一个通项公式为an=n+ = (n∈N*).
(3)原数列的各项可变为 ×9, ×99, ×999, ×9 999,…,易知数列
9,99,999,9 999,…的一个通项公式为an=10n-1,所以原数列的一个通项公式为
an= (10n-1)(n∈N*).
【加练·固】
根据下面数列的前几项的值,写出数列的一个通项公式:
(1) 3,5,7,9,11,13,…;
(2) , , , , , …;
(3) 0, 1, 0, 1, 0, 1,…;
(4) 1, 3, 3, 5, 5, 7, 7, 9, 9,…;
(5) 2, -6, 12, -20, 30, -42,….
【解析】(1)从3开始的奇数列,an=2n+1.
(2)分子为偶数,分母为相邻两奇数的积
an=
(4) 将数列变形为1+0, 2+1, 3+0, 4+1, 5+0, 6+1, 7+0, 8+1, …,
所以
(5) 将数列变形为1×2, -2×3, 3×4, -4×5, 5×6,…,
所以an=(-1)n+1n(n+1).
类型三 数列通项公式的简单应用
【典例】已知数列{an}的通项公式为an= .
(1)求a10.
(2)判断 是否为该数列中的项.若是,它为第几项 若不是,请说明理由.
(3)求证:0【思维·引】(1)将n=10代入{an}的通项公式即可求a10.
(2)令an= ,若n为正整数,则 是{an}的项,否则,不是{an}的项.
(3)分离常数后可证.
【解析】(1)根据题意可得a10=
(2)令an= ,即 = ,解得n=3,
所以 为数列{an}中的项,为第3项.
(3)由题知an= =1- ,
因为n∈N*,所以3n+1>3,所以0< <1,
所以0<1- <1,即0【类题·通】
1.利用数列的通项公式求某项的方法
数列的通项公式给出了第n项an与它的位置序号n之间的关系,只要用序号代替公式中的n,就可以求出数列的相应项.
2.判断某数值是否为该数列的项的方法
先假定它是数列中的第n项,然后列出关于n的方程.若方程解为正整数则是数列的一项;若方程无解或解不是正整数,则不是该数列的一项.
【习练·破】
数列{an}的通项公式为an=30+n-n2.
(1)-60是否是{an}中的一项
(2)当n分别取何值时,an=0,an>0,an<0
【解析】(1)假设-60是{an}中的一项,
则-60=30+n-n2.
解得n=10或n=-9(舍去).
所以-60是{an}的第10项.
(2)分别令30+n-n2=0;30+n-n2>0;
30+n-n2<0,
解得n=6;06,
即n=6时,an=0;
当00;
当n>6且n∈N*时,an<0.
【加练·固】
已知数列{an}的通项公式为an= .
(1)写出数列的第4项和第6项.
(2)试问 是该数列的项吗 若是,是第几项 若不是,请说明理由.
【解析】(1)因为an= ,
所以a4= = ,a6= = .
(2)令 = ,则n2+3n-40=0,
解得n=5或n=-8,注意到n∈N*,
故将n=-8舍去,所以 是该数列的第5项.
1.有下列命题:
①数列 …的一个通项公式是an=
②数列的图象是一群孤立的点;
③数列1,-1,1,-1,…与数列-1, 1,-1,1,…是同一数列;
④数列 是递增数列.
其中正确命题的个数为 ( )
A.1 B.2 C.3 D.0
【解析】选A.由通项公式知a1= ≠ ,故①不正确;易知②正确;由于两数列中
数的排列次序不同,因此不是同一数列,故③不正确;④中的数列为递减数列,
所以④不正确.
2.数列 …的一个通项公式是 ( )
【解析】选B.因为数列 …的第三项可写成 这样,每一项都
是含根号的数,且每一个被开方数比前一项的被开方数多3,所以an=
3.在数列{an}中,an=51-n,则a3等于________.
【解析】由已知得a3=51-3= .
答案:
4.在数列{an}中,已知an= n∈N*,则 是数列
中的第________项.
【解析】根据题意,数列{an}中,已知an=
若 即n2+n-1=19,解得:n=4或-5(舍).
答案:4
【新情境·新思维】
大衍数列来源于《乾坤谱》中对易传“大衍之数五十”的推论,主要用于解释中国传统文化中的太极衍生原理,数列中的每一项,都代表太极衍生过程中曾经经历过的两仪数量总和,它是中华传统文化中隐藏着的世界数学史上第一道数列题,该数列从第一项起依次是0,2,4,8,12,18,24,32,40,50,…,求该数列的第18项.
【解析】由题意得,偶数项分别为2,8,18,32,50,…可发现规律为:
2=2×1=2×12=2×
8=2×4=2×22=2×
18=2×9=2×32=2×
32=2×16=2×42=2×
50=2×25=2×52=2× …
则该数列第18项为2× =2×92=2×81=162.
4.1数列的概念
第1课时 数列的概念与简单表示法
答辩人:亮亮图文
1.数列及其相关概念
(1)定义:按___________排列的一列数叫做数列.
(2)项:数列中的_________叫做这个数列的项.
(3)形式:a1,a2,a3,…,an,…,简记为{an},其中an是数列的第__项,第1项也叫做
首项.
确定的顺序
每一个数
n
【思考】
(1)如果组成两个数列的数相同但排列次序不同,那么它们是相同的数列吗
提示:从数列的定义可以看出,组成数列的数是按一定顺序排列的,如果组成数列的数相同但排列次序不同,那么它们就不是同一数列.
(2)同一个数在数列中可以重复出现吗
提示:在数列的定义中,并没有规定数列中的数必须不同,因此,同一个数在数列中可以重复出现.例如:1,-1,1,-1,1,…;2,2,2,….
2.数列的分类
分类标准 名称 含义
按项的 个数 有穷数列 项数_____的数列
无穷数列 项数_____的数列
按项的 变化趋势 递增数列 从第2项起,每一项都_____它的前一项的数列
递减数列 从第2项起,每一项都_____它的前一项的数列
常数列 各项都_____的数列
摆动数列 从第2项起,有些项大于它的前一项,有些项小于它的前一项的数列
有限
无限
大于
小于
相等
3.函数与数列的关系
数列{an}是从________(或它的有限子集{1,2,…,n})到实数集R的函数,自变量
是序号n,对应的函数值是数列的第n项an,记为an=f(n).
正整数N*
4.数列的通项公式:如果数列{an}的第n项an与它的序号n之间的对应关系可以
用_________来表示,那么这个式子叫做这个数列的通项公式.
一个式子
1.思维辨析(对的打“√”,错的打“×”)
(1)1,2,3,4和1,2,4,3是相同的数列. ( )
(2){an}与an是一样的,都表示数列. ( )
(3)所有数列都能写出其通项公式且一个数列的通项公式是唯一的. ( )
(4)数列3,1,-1,-3,-5,-10的通项公式为an=5-2n.( )
提示:(1)×.两个数列相同,每一项都必须相同,而且数列具有顺序性.
(2)×.因为{an}代表一个数列,而an只是这个数列中的第n项,故{an}与an是不一样的.
(3)×.有的数列就没有通项公式,而且有的数列的通项公式不唯一.
(4)×. 第六项为-10,不符合an=5-2n,故an=5-2n不是此数列的通项公式.
2.数列3,4,5,6,…的一个通项公式为 ( )
A.an=n,n∈N* B.an=n+1,n∈N*
C.an=n+2,n∈N* D.an=2n,n∈N*
【解析】选C.这个数列的前4项都比序号大2,所以,它的一个通项公式为an=n+2,n∈N*.
3.已知数列{an}的通项公式是an=n2+1,则122是该数列的 ( )
A.第9项 B.第10项 C.第11项 D.第12项
【解析】选C.令n2+1=122,则n2=121,
所以n=11或n=-11(舍去).
4.已知数列{an}的通项公式是an=2n-1,则a8=________.
【解析】a8=2×8-1=15.
答案:15
题型一 数列的概念以及分类
【典例】1.下列说法错误的是 ( )
A.数列4,7,3,4的首项是4
B.数列{an}中,若a1=3,则从第2项起,各项均不等于3
C.数列1,2,3,…就是数列{n}
D.数列中的项不能是三角形
2.已知下列数列:
①2 011,2 012,2 013,2 014,2 015,2 016;
②1, , ,…, ,…;
③1,- , ,…, ,…;
④1,0,-1,…,sin ,…;
⑤2,4,8,16,32,…;
⑥-1,-1,-1,-1.
其中,有穷数列是________,无穷数列是________,递增数列是________,递减数列是________,常数列是________,摆动数列是________(填序号).
【思维·引】1.依据数列的定义逐项判断.
2.依据数列分类中有关数列的定义,逐个判断.
【解析】1.选B.由数列的相关概念可知,数列4,7,3,4的首项是4,故A正确.
同一个数在数列中可以重复出现,故B错误.
按一定顺序排列的一列数称为数列,所以数列1,2,3,…就是数列{n},故C正确.
数列中的项必须是数,不能是其他形式,故D正确.
2.①为有穷数列且为递增数列;②为无穷数列、递减数列;③为无穷数列、摆动数列;④是摆动数列,也是无穷数列;⑤为递增数列,也是无穷数列;⑥为有穷数列,也是常数列.
答案:①⑥ ②③④⑤ ①⑤ ② ⑥ ③④
【内化·悟】
1.与集合中元素的性质相比较,数列中的项的性质具有哪些特点
提示:(1)确定性:一个数是或不是某一数列中的项是确定的,集合中的元素也具有确定性;
(2)可重复性:数列中的数可以重复,而集合中的元素不能重复出现(即互异性);
(3)有序性:一个数列不仅与构成数列的“数”有关,而且与这些数的排列顺序有关,而集合中的元素没有顺序(即无序性);
(4)数列中的每一项都是数,而集合中的元素还可以代表除数字外的其他事物.
2.如何判断两个数列是相同数列
提示:组成数列的数相同,且排列次序也相同的两个数列才是相同的数列.
【类题·通】
数列概念的三个注意点
(1)数列{an}表示数列a1,a2,a3,…,an,…,不是表示一个集合,与集合表示有本质的区别.
(2)从数列的定义可以看出,如果组成数列的数相同而排列次序不同,那么它们就是不同的数列;在定义中,并没有规定数列中的数必须不同,因此,同一个数在数列中可以重复出现.
(3)数列中各项的次序揭示了数列的规律性,是理解、把握数列的关键.
【习练·破】
下列数列中,既是无穷数列又是递增数列的是 ( )
A.1, , ,…
B.sin ,sin ,sin ,sin ,…
C.-1,- ,- ,- ,…
D.1,2,3,4,…,30
【解析】选C.数列1, , ,…是无穷数列,但它不是递增数列,而是递减
数列;数列sin ,sin ,sin ,sin ,…是无穷数列,但它既不是递增数
列,又不是递减数列;数列-1,- ,- ,- ,…是无穷数列,也是递增数列;数列
1,2,3,4,…,30是递增数列,但不是无穷数列.
【加练·固】
下列数列
(1)1,2,22,23,…,263;
(2)0,10,20,30,…,1 000;
(3)2,4,6,8,10,…;
(4)-1,1,-1,1,-1,…;
(5)7,7,7,7,…;
(6)
其中有穷数列是________,无穷数列是________,递增数列是________,递减数列是________,摆动数列是________,常数列是________.(填序号)
【解析】根据数列的概念知有穷数列是(1)(2),无穷数列是 (3)(4)(5)(6),递增数列是(1)(2)(3),递减数列是(6),摆动数列是 (4),常数列是(5).
答案:(1)(2) (3)(4)(5)(6) (1)(2)(3) (6) (4) (5)
类型二 观察法写出数列的通项公式
【典例】1.(2020·徐州高一检测)数列3,6,11,20,…的一个通项公式为
( )
A.an=3n B.an=n(n+2)
C.an=n+2n D.an=2n+1
2.写出下列数列的一个通项公式:
(1) ,2, ,8, ,…;
(2)1,-3,5,-7,9,…;
(3)9,99,999,9 999,…;
(4) …;
(5) …;
(6)4,0,4,0,4,0,….
【思维·引】1.根据特点,观察、分析,寻找数列的每一项与其所在项的序号之间的关系,归纳出一个通项公式即可.
2.首先要熟悉一些常见数列的通项公式,然后对于复杂数列的通项公式,其项与序号之间的关系不容易发现,要将数列各项的结构形式加以变形,将数列的各项分解成若干个常见数列对应项的“和”“差”“积”“商”后再进行归纳.
【解析】1.选C.依题意,a1=3=1+21;a2=6=2+22;a3=11=3+23;a4=20=4+24;…,
所以an=n+2n.
2.(1)数列的项有的是分数,有的是整数,可先将各项都统一成分数再观察:
…,所以,它的一个通项公式为an= .
(2)数列各项的绝对值分别为1,3,5,7,9,…是连续的正奇数,其通项公式为2n
-1;考虑(-1)n+1具有转换符号的作用,所以数列的一个通项公式为an=(-1)n+1(2n
-1).
(3)各项加1后,分别变为10,100,1 000,10 000,…此数列的通项公式为10n,可
得原数列的一个通项公式为an=10n-1.
(4)数列中每一项均由三部分组成,分母是从1开始的奇数列,其通项公式为2n-
1;分子的前一部分是从2开始的自然数的平方,分子的后一部分是减去一个从1
开始的自然数,综合得原数列的一个通项公式为an=
(5)这个数列的前4项的绝对值都等于序号与序号加1的积的倒数,且奇数项为
负,偶数项为正,所以它的一个通项公式是an=(-1)n·
(6)由于该数列中,奇数项全部都是4,偶数项全部都是0,因此可用分段函数的
形式表示通项公式,即an=
又因为数列可改写为2+2,2-2,2+2,2-2,2+2,2-2,…,因此其通项公式又可表示
为an=2+2×(-1)n+1.
【素养·探】
在与观察法写出数列的通项公式有关的问题中,经常利用核心素养中的逻辑推理,通过研究数列的前几项与项的序号之间的关系,归纳出数列的通项公式.
将本例2(6)的数列改为“3,5,3,5,3,5,…”,如何写出其通项公式
【解析】此数列的奇数项为3,偶数项为5,故通项公式可写为an=
此数列两项3与5的平均数为 =4,
奇数项为4-1,偶数项为4+1,
故通项公式还可写为an=4+(-1)n.
【类题·通】
(1)用观察法求数列通项公式的策略
(2)对于符号交替出现的情况,可先观察其绝对值,再用(-1)k处理符号问题.
(3)对于周期出现的数列,可考虑拆成几个简单数列和的形式,或者利用周期函数,如三角函数等.
【习练·破】
写出下列数列的一个通项公式:
(1)0,3,8,15,24,…;
(2)1 ,2 ,3 ,4 ,…;
(3)1,11,111,1 111,….
【解析】(1)观察数列中的数,可以看到0=1-1,3=4-1,8=9-1,15=16-1,24=25-1,
…,所以它的一个通项公式是an=n2-1(n∈N*).
(2)此数列的整数部分1,2,3,4,…恰好是序号n,分数部分与序号n的关系为
故所求的数列的一个通项公式为an=n+ = (n∈N*).
(3)原数列的各项可变为 ×9, ×99, ×999, ×9 999,…,易知数列
9,99,999,9 999,…的一个通项公式为an=10n-1,所以原数列的一个通项公式为
an= (10n-1)(n∈N*).
【加练·固】
根据下面数列的前几项的值,写出数列的一个通项公式:
(1) 3,5,7,9,11,13,…;
(2) , , , , , …;
(3) 0, 1, 0, 1, 0, 1,…;
(4) 1, 3, 3, 5, 5, 7, 7, 9, 9,…;
(5) 2, -6, 12, -20, 30, -42,….
【解析】(1)从3开始的奇数列,an=2n+1.
(2)分子为偶数,分母为相邻两奇数的积
an=
(4) 将数列变形为1+0, 2+1, 3+0, 4+1, 5+0, 6+1, 7+0, 8+1, …,
所以
(5) 将数列变形为1×2, -2×3, 3×4, -4×5, 5×6,…,
所以an=(-1)n+1n(n+1).
类型三 数列通项公式的简单应用
【典例】已知数列{an}的通项公式为an= .
(1)求a10.
(2)判断 是否为该数列中的项.若是,它为第几项 若不是,请说明理由.
(3)求证:0
(2)令an= ,若n为正整数,则 是{an}的项,否则,不是{an}的项.
(3)分离常数后可证.
【解析】(1)根据题意可得a10=
(2)令an= ,即 = ,解得n=3,
所以 为数列{an}中的项,为第3项.
(3)由题知an= =1- ,
因为n∈N*,所以3n+1>3,所以0< <1,
所以0<1- <1,即0
1.利用数列的通项公式求某项的方法
数列的通项公式给出了第n项an与它的位置序号n之间的关系,只要用序号代替公式中的n,就可以求出数列的相应项.
2.判断某数值是否为该数列的项的方法
先假定它是数列中的第n项,然后列出关于n的方程.若方程解为正整数则是数列的一项;若方程无解或解不是正整数,则不是该数列的一项.
【习练·破】
数列{an}的通项公式为an=30+n-n2.
(1)-60是否是{an}中的一项
(2)当n分别取何值时,an=0,an>0,an<0
【解析】(1)假设-60是{an}中的一项,
则-60=30+n-n2.
解得n=10或n=-9(舍去).
所以-60是{an}的第10项.
(2)分别令30+n-n2=0;30+n-n2>0;
30+n-n2<0,
解得n=6;0
即n=6时,an=0;
当0
当n>6且n∈N*时,an<0.
【加练·固】
已知数列{an}的通项公式为an= .
(1)写出数列的第4项和第6项.
(2)试问 是该数列的项吗 若是,是第几项 若不是,请说明理由.
【解析】(1)因为an= ,
所以a4= = ,a6= = .
(2)令 = ,则n2+3n-40=0,
解得n=5或n=-8,注意到n∈N*,
故将n=-8舍去,所以 是该数列的第5项.
1.有下列命题:
①数列 …的一个通项公式是an=
②数列的图象是一群孤立的点;
③数列1,-1,1,-1,…与数列-1, 1,-1,1,…是同一数列;
④数列 是递增数列.
其中正确命题的个数为 ( )
A.1 B.2 C.3 D.0
【解析】选A.由通项公式知a1= ≠ ,故①不正确;易知②正确;由于两数列中
数的排列次序不同,因此不是同一数列,故③不正确;④中的数列为递减数列,
所以④不正确.
2.数列 …的一个通项公式是 ( )
【解析】选B.因为数列 …的第三项可写成 这样,每一项都
是含根号的数,且每一个被开方数比前一项的被开方数多3,所以an=
3.在数列{an}中,an=51-n,则a3等于________.
【解析】由已知得a3=51-3= .
答案:
4.在数列{an}中,已知an= n∈N*,则 是数列
中的第________项.
【解析】根据题意,数列{an}中,已知an=
若 即n2+n-1=19,解得:n=4或-5(舍).
答案:4
【新情境·新思维】
大衍数列来源于《乾坤谱》中对易传“大衍之数五十”的推论,主要用于解释中国传统文化中的太极衍生原理,数列中的每一项,都代表太极衍生过程中曾经经历过的两仪数量总和,它是中华传统文化中隐藏着的世界数学史上第一道数列题,该数列从第一项起依次是0,2,4,8,12,18,24,32,40,50,…,求该数列的第18项.
【解析】由题意得,偶数项分别为2,8,18,32,50,…可发现规律为:
2=2×1=2×12=2×
8=2×4=2×22=2×
18=2×9=2×32=2×
32=2×16=2×42=2×
50=2×25=2×52=2× …
则该数列第18项为2× =2×92=2×81=162.
