正方形习题课

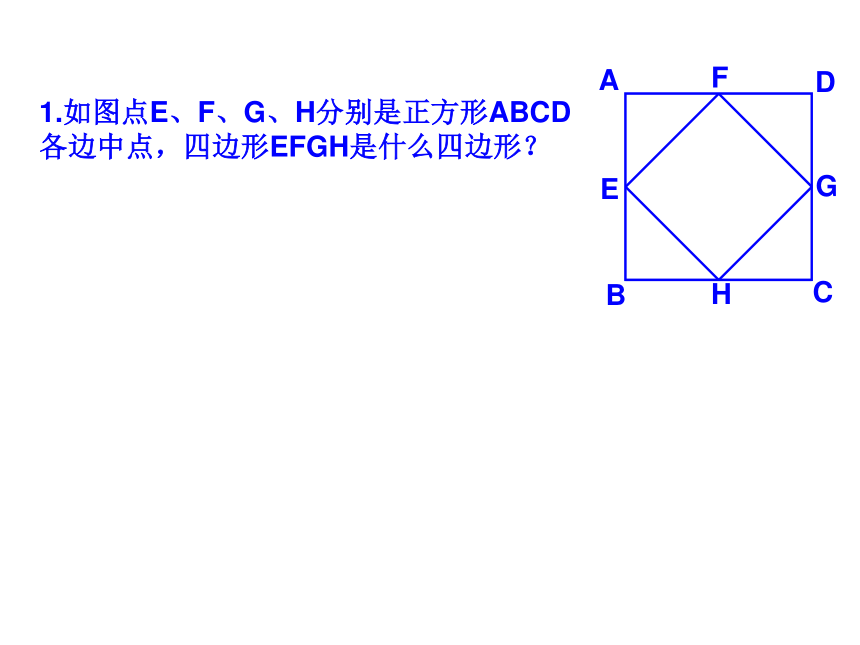
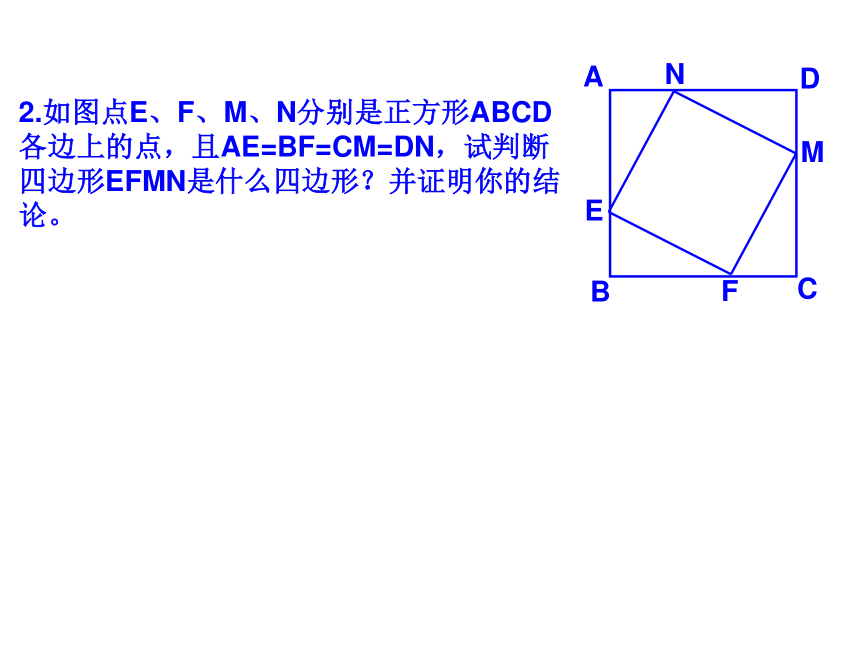
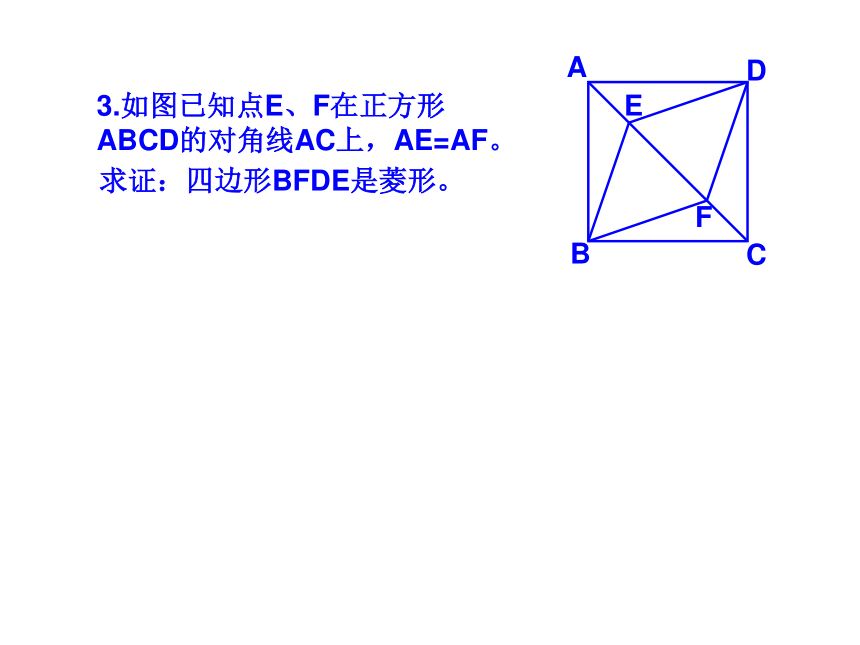
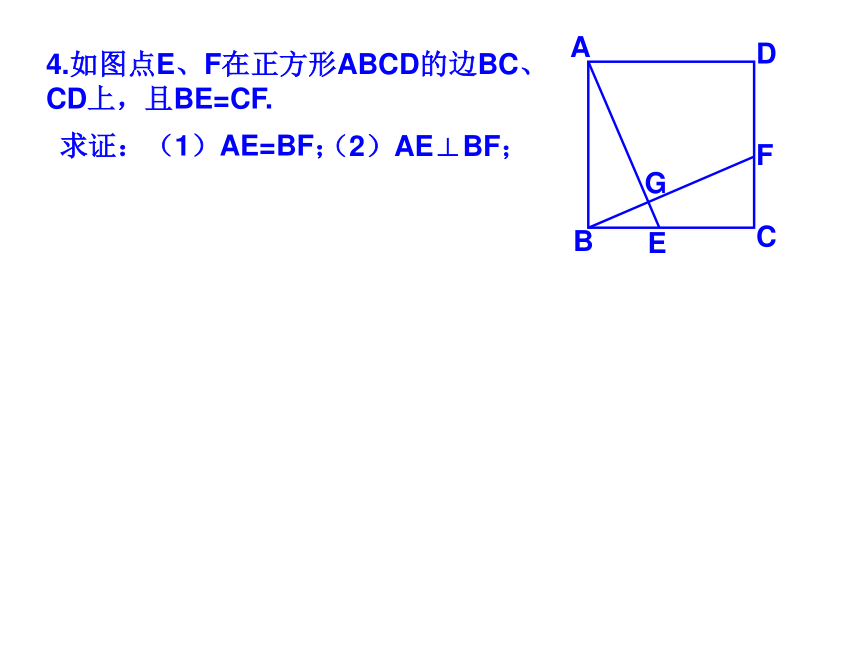
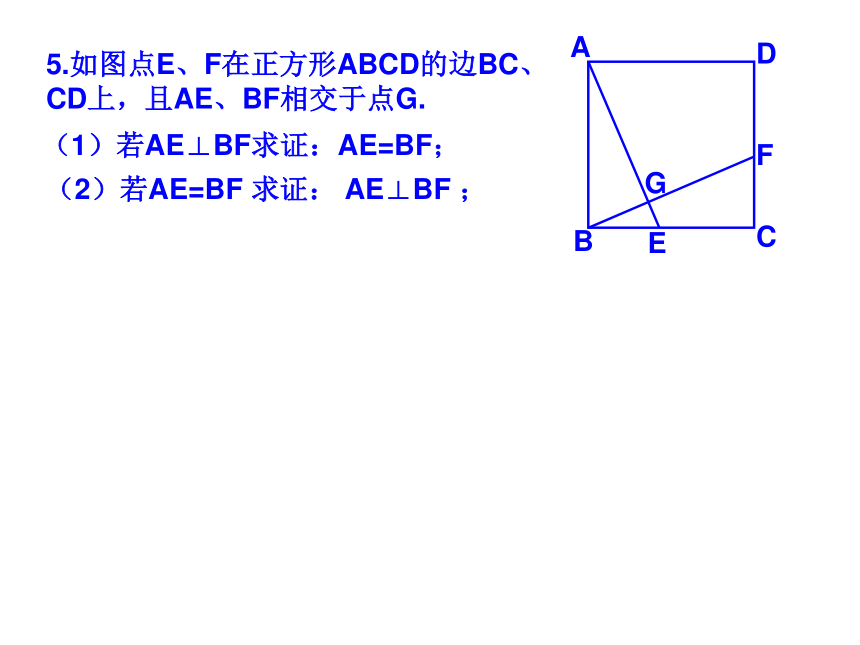
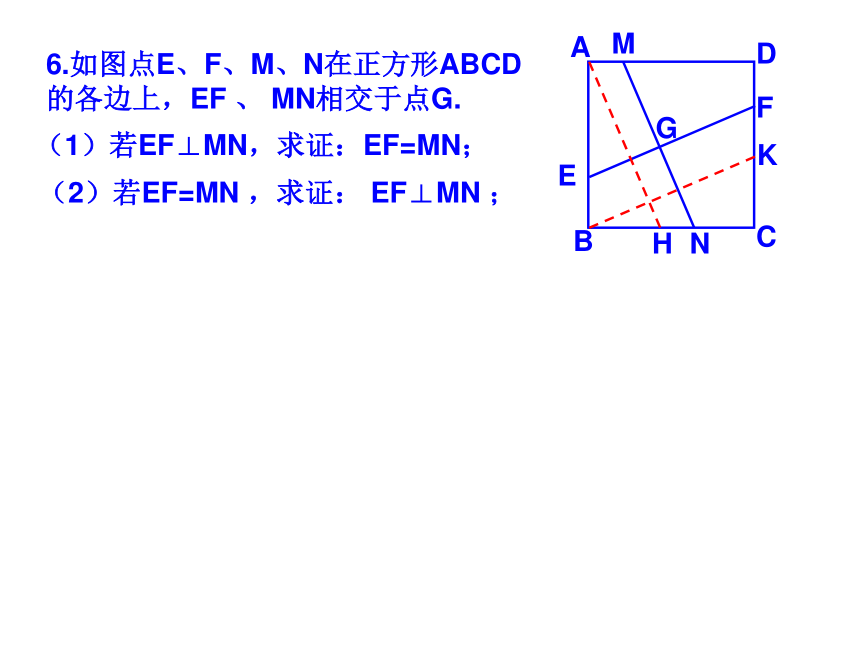
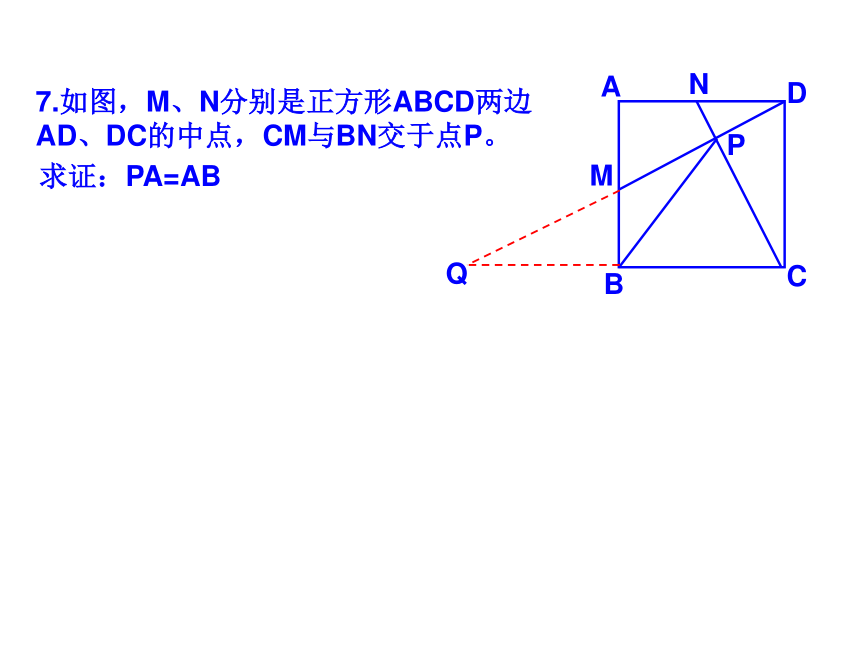
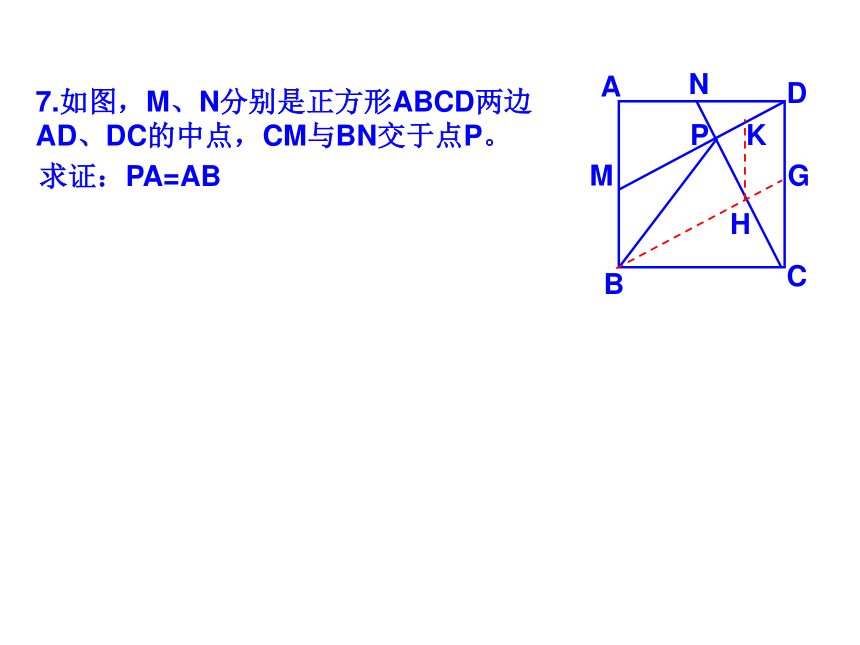
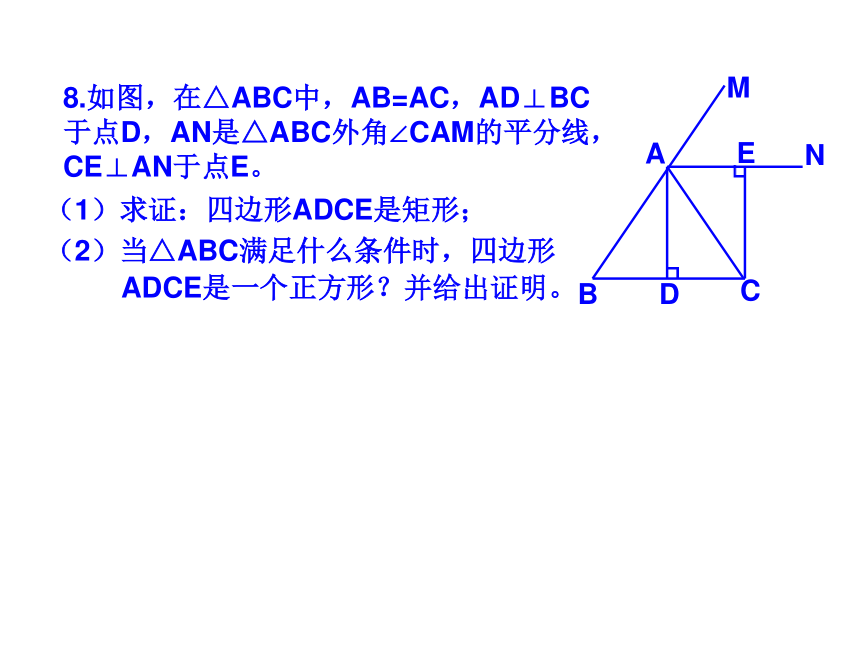
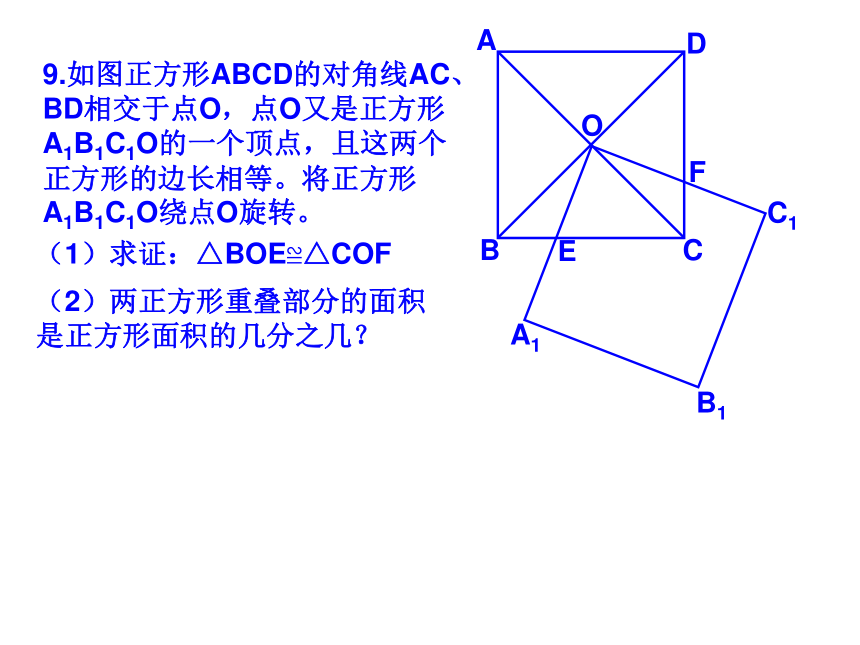
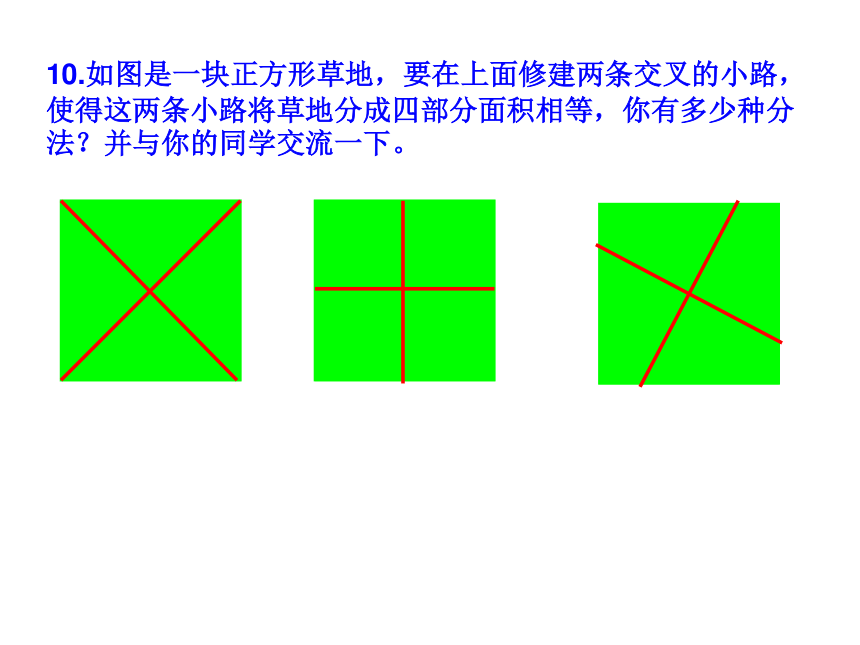
课件35张PPT。 19.2正方形2009.5.191.如图点E、F、G、H分别是正方形ABCD各边中点，四边形EFGH是什么四边形？2.如图点E、F、M、N分别是正方形ABCD各边上的点，且AE=BF=CM=DN，试判断四边形EFMN是什么四边形？并证明你的结论。5.如图点E、F在正方形ABCD的边BC、CD上，且AE、BF相交于点G.（1）若AE⊥BF求证：AE=BF； （2）若AE=BF 求证： AE⊥BF ； 6.如图点E、F、M、N在正方形ABCD的各边上，EF 、 MN相交于点G.（1）若EF⊥MN，求证：EF=MN； DABCEFG（2）若EF=MN ，求证： EF⊥MN ； MNHK7.如图，M、N分别是正方形ABCD两边AD、DC的中点，CM与BN交于点P。求证：PA=ABQ7.如图，M、N分别是正方形ABCD两边AD、DC的中点，CM与BN交于点P。求证：PA=ABDABCMPNGHK8.如图，在△ABC中，AB=AC，AD⊥BC于点D，AN是△ABC外角∠CAM的平分线，CE⊥AN于点E。（1）求证：四边形ADCE是矩形；（2）当△ABC满足什么条件时，四边形ADCE是一个正方形？并给出证明。9.如图正方形ABCD的对角线AC、BD相交于点O，点O又是正方形A1B1C1O的一个顶点，且这两个正方形的边长相等。将正方形A1B1C1O绕点O旋转。（1）求证：△BOE≌△COFABCDOA1B1C1EF（2）两正方形重叠部分的面积是正方形面积的几分之几？10.如图是一块正方形草地，要在上面修建两条交叉的小路，使得这两条小路将草地分成四部分面积相等，你有多少种分法？并与你的同学交流一下。11.如图正方形ABCD和正方形BEFG，A、B、E在同一直线上，连接AG、CE。试探索AG、CE之间的关系，并证明你的结论。11.将正方形BGFE绕点B顺时针旋转α（0°<α <90°）,探究AG、CE的关系，并证明你的结论。12.如图正方形ABCD和正方形BEFG，A、B、E在同一直线上，且四边形AGHD是平行四边形，试探索DH、HF之间的关系，并证明你的结论。12.将正方形BGFE绕点B顺时针旋转α（0°<α <90°）,探究DH、HF的关系，并证明你的结论。ABCDEFGH12.将正方形BGFE绕点B顺时针旋转α（0°<α <90°）,探究DH、HF的关系，并证明你的结论。ABCDEFGH13.如图，AC为正方形ABCD的对角线。操作：在图中，将一把三角尺的直角顶点P放在AC上，沿AC边滑动三角尺，使得直角的一边经过点B，另一边与射线DC相交于点Q。ABCDQP13.如图，AC为正方形ABCD的对角线。操作：在图中，将一把三角尺的直角顶点P放在AC上，沿AC边滑动三角尺，使得直角的一边经过点B，另一边与射线DC相交于点Q。ABCDQP13.如图，AC为正方形ABCD的对角线。操作：在图中，将一把三角尺的直角顶点P放在AC上，沿AC边滑动三角尺，使得直角的一边经过点B，另一边与射线DC相交于点Q。ABCDQP13.如图，AC为正方形ABCD的对角线。操作：在图中，将一把三角尺的直角顶点P放在AC上，沿AC边滑动三角尺，使得直角的一边经过点B，另一边与射线DC相交于点Q。ABCDQP13.如图，AC为正方形ABCD的对角线。操作：在图中，将一把三角尺的直角顶点P放在AC上，沿AC边滑动三角尺，使得直角的一边经过点B，另一边与射线DC相交于点Q。ABCDQP13.如图，AC为正方形ABCD的对角线。操作：在图中，将一把三角尺的直角顶点P放在AC上，沿AC边滑动三角尺，使得直角的一边经过点B，另一边与射线DC相交于点Q。ABCDQP13.如图，AC为正方形ABCD的对角线。操作：在图中，将一把三角尺的直角顶点P放在AC上，沿AC边滑动三角尺，使得直角的一边经过点B，另一边与射线DC相交于点Q。ABCDQP13.如图，AC为正方形ABCD的对角线。操作：在图中，将一把三角尺的直角顶点P放在AC上，沿AC边滑动三角尺，使得直角的一边经过点B，另一边与射线DC相交于点Q。ABCDQP13.如图，AC为正方形ABCD的对角线。操作：在图中，将一把三角尺的直角顶点P放在AC上，沿AC边滑动三角尺，使得直角的一边经过点B，另一边与射线DC相交于点Q。ABCDQP13.如图，AC为正方形ABCD的对角线。操作：在图中，将一把三角尺的直角顶点P放在AC上，沿AC边滑动三角尺，使得直角的一边经过点B，另一边与射线DC相交于点Q。ABCDQP探究：（1）当点Q在边CD边上时，线段PQ与线段PB之间有怎样的大小关系？试证明你观察得到的结论；探究：（2）当点Q在边CD延长线上时，（1）结论是否依然成立？说明理由；探究（3）当点P在线段AC上滑动时（P不与A重合），△PCQ是否可能成为等腰三角形？如果可能，指出所有能使△PCQ成为等腰三角形的点Q的位置，并求出此时线段AB、PA两者的数量关系。14.正方形ABCD与正方形CEFG有公共顶点C，点P为AF的中点。（1）如图放置时，猜想PB与PE的关系，并证明你的结论。FECBADPG14.ABCD与正方形CEFG有公共顶点C，点P为AF的中点。（2）如图放置时，猜想PB与PE的关系，并证明你的结论。14.ABCD与正方形CEFG有公共顶点C，点P为AF的中点。（3）如图放置时，猜想PB与PE的关系，并证明你的结论。15.四边形ABCD是正方形，其对角线AC、BD交于点O，点P为AD边上的动点，PE⊥AC于E，M是AD的中点，连接OE、OF。（1）如图，求证：ME=MF （2）如图当四边形ABCD为矩形时，其他条件不变，上述结论还成立吗？如果成立请证明；如果不成立，其说明理由。（3）当四边形ABCD为一般四边形时，其他条件不变，上述结论还成立吗？如果成立，请证明；如果不成立，那么添加一个什么条件，可使上述结论成立？并完成证明。