鲁教版九年级数学上册第2单元三角函数的应用同步辅导(含答案)
文档属性
| 名称 | 鲁教版九年级数学上册第2单元三角函数的应用同步辅导(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 228.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-10-01 00:00:00 | ||
图片预览


文档简介
鲁教版九年级数学上册第2单元三角函数的应用同步辅导(含答案)
一.选择题(共12小题)
1.(2015 新泰市二模)如图,为安全起见,萌萌拟加长滑梯,将其倾斜角由45°降至30°.已知滑梯AB的长为3m,点D、B、C在同一水平地面上,那么加长后的滑梯AD的长是( )
A.2 B. 2 C. 3 D. 3m
(1题图) (2题图) (3题图)
2.(2014 随州)如图,要测量B点到河岸AD的距离,在A点测得∠BAD=30°,在C点测得∠BCD=60°,又测得AC=100米,则B点到河岸AD的距离为( )
A.100米 B. 50米 C. 米 D. 50米
3.(2014 白云区校级模拟)如图,两个高度相等的圆柱形水杯,甲杯装满液体,乙杯是空杯.若把甲杯中的液体全部倒入乙杯,则乙杯中的液面与图中点P的距离是( )
A.2cm B. 4cm C. 6cm D. 8cm
4.(2014 山西模拟)如图,沿AB方向开山修路,为了加快施工进度,要在小山的另一边同时施工,从AB上的一点C,取∠ACD=146°,CD=500m,∠D=56°.要使点A,C,E在同一条直线上,那么开挖点E离点D的距离是( )
A.500m B. 500sin56°m C. 500cos56°m D. 500tan56°m
(4题图) (5题图) (6题图)
5.(2015 祁阳县三模)如图,河堤横断面迎水坡AB的坡比是1:,堤高BC=10m,则坡面AB的长度是(
A. 15m B. 20m C. 20m D. 10m
6.如图,一水库大坝的横断面为梯形ABCD,坝顶BC宽6米,坝高20米,斜坡AB的坡度i=1:2.5,斜坡CD的坡角为30度,则坝底AD的长度为( )
A. 56米 B. 66米 C. (56+20)米 D. (50+20)米
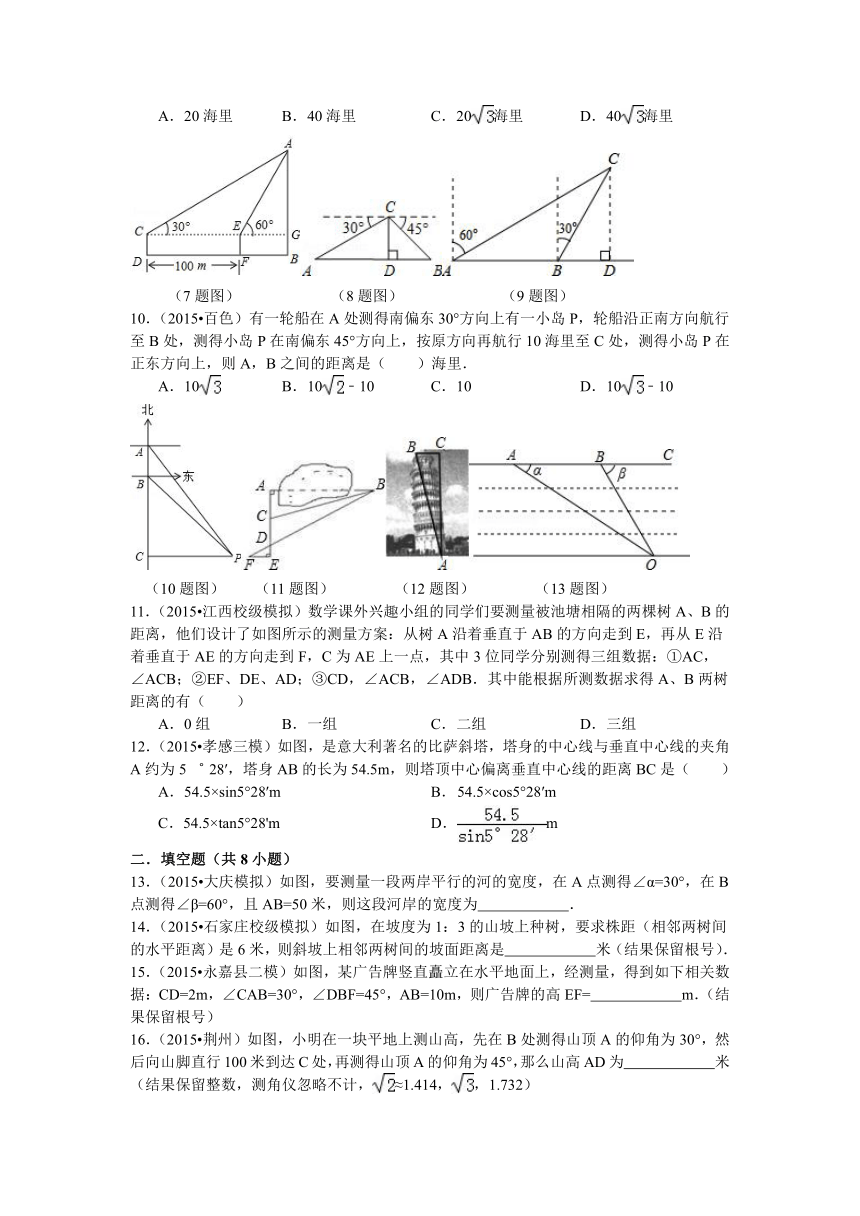
7.(2015 衡阳)如图,为了测得电视塔的高度AB,在D处用高为1米的测角仪CD,测得电视塔顶端A的仰角为30°,再向电视塔方向前进100米达到F处,又测得电视塔顶端A的仰角为60°,则这个电视塔的高度AB(单位:米)为( )
A.50 B. 51 C. 50+1 D. 101
8.(2015 南丹县一模)如图,在热气球C处测得地面A、B两点的俯角分别为30°、45°,热气球C的高度CD为100米,点A、D、B在同一直线上,则AB两点的距离是( )
A.200米 B. 200米 C. 220米 D. 米
9.如图,一渔船由西往东航行,在A点测得海岛C位于北偏东60°的方向,前进40海里到达B点,此时,测得海岛C位于北偏东30°的方向,则海里C到航线AB的距离CD是( )
A.20海里 B. 40海里 C. 20海里 D. 40海里
(7题图) (8题图) (9题图)
10.(2015 百色)有一轮船在A处测得南偏东30°方向上有一小岛P,轮船沿正南方向航行至B处,测得小岛P在南偏东45°方向上,按原方向再航行10海里至C处,测得小岛P在正东方向上,则A,B之间的距离是( )海里.
A.10 B. 10﹣10 C. 10 D. 10﹣10
(10题图) (11题图) (12题图) (13题图)
11.(2015 江西校级模拟)数学课外兴趣小组的同学们要测量被池塘相隔的两棵树A、B的距离,他们设计了如图所示的测量方案:从树A沿着垂直于AB的方向走到E,再从E沿着垂直于AE的方向走到F,C为AE上一点,其中3位同学分别测得三组数据:①AC,∠ACB;②EF、DE、AD;③CD,∠ACB,∠ADB.其中能根据所测数据求得A、B两树距离的有( )
A.0组 B. 一组 C. 二组 D. 三组
12.(2015 孝感三模)如图,是意大利著名的比萨斜塔,塔身的中心线与垂直中心线的夹角A约为5゜28′,塔身AB的长为54.5m,则塔顶中心偏离垂直中心线的距离BC是( )
A.54.5×sin5°28′m B. 54.5×cos5°28′m
C.54.5×tan5°28'm D. m
二.填空题(共8小题)
13.(2015 大庆模拟)如图,要测量一段两岸平行的河的宽度,在A点测得∠α=30°,在B点测得∠β=60°,且AB=50米,则这段河岸的宽度为 .
14.(2015 石家庄校级模拟)如图,在坡度为1:3的山坡上种树,要求株距(相邻两树间的水平距离)是6米,则斜坡上相邻两树间的坡面距离是 米(结果保留根号).
15.(2015 永嘉县二模)如图,某广告牌竖直矗立在水平地面上,经测量,得到如下相关数据:CD=2m,∠CAB=30°,∠DBF=45°,AB=10m,则广告牌的高EF= m.(结果保留根号)
16.(2015 荆州)如图,小明在一块平地上测山高,先在B处测得山顶A的仰角为30°,然后向山脚直行100米到达C处,再测得山顶A的仰角为45°,那么山高AD为 米(结果保留整数,测角仪忽略不计,≈1.414,,1.732)
(14题图) (15题图) (16题图)
17.(2015 大连模拟)为了缓解长沙市区内一些主要路段交通拥挤的现状,交警队在一些主要路口设立了交通路况显示牌(如图).已知立杆AB高度是3m,从侧面D点测得显示牌顶端C点和底端B点的仰角分别是60°和45°.则路况显示牌BC的高度为 米.
(17题图) (18题图) (19题图) (20题图)
18.某中学初三年级的学生开展测量物体高度的实践活动,他们要测量一幢建筑物AB的高度.如图,他们先在点C处测得建筑物AB的顶点A的仰角为30°,然后向建筑物AB前进20m到达点D处,又测得点 A的仰角为60°,则建筑物AB的高度是 m.
19.(2015 宁夏)如图,港口A在观测站O的正东方向,OA=4km,某船从港口A出发,沿北偏东15°方向航行一段距离后到达B处,此时从观测站O处测得该船位于北偏东60°的方向,则该船航行的距离(即AB的长)为 .
20.(2015 湖北模拟)一艘观光游船从港口A以北偏东60°的方向出港观光,航行60海里至C处时发生了侧翻沉船事故,立即发出了求救信号,一艘在港口正东方向的海警船接到求救信号,测得事故船在它的北偏东30°方向,马上以40海里每小时的速度前往救援,海警船到达事故船C处所需的时间大约为 小时(用根号表示).
三.解答题(共6小题)
21.(2015 自贡)如图所示,我市某中学课外活动小组的同学利用所学知识去测量釜溪河沙湾段的宽度.小宇同学在A处观测对岸C点,测得∠CAD=45°,小英同学在距A处50米远的B处测得∠CBD=30°,请你根据这些数据算出河宽.(精确到0.01米,参考数据≈1.414,≈1.732)
22.(2015 贺州)根据道路管理规定,在贺州某段笔直公路上行驶的车辆,限速40千米/时,已知交警测速点M到该公路A点的距离为10米,∠MAB=45°,∠MBA=30°(如图所示),现有一辆汽车由A往B方向匀速行驶,测得此车从A点行驶到B点所用的时间为3秒.
(1)求测速点M到该公路的距离;
(2)通过计算判断此车是否超速.(参考数据:≈1.41,≈1.73,≈2.24)
23.(2015 安徽模拟)如图,某滑板爱好者训练时的斜坡示意图,出于安全因素考虑,决定将训练的斜坡的倾角由45°降为30°,已知原斜坡坡面AB的长为5米,点D、B、C在同一水平地面上.
(1)改善后斜坡坡面AD比原斜坡坡面AB会加长多少米?(精确到0.01)
(2)若斜坡的正前方能有3米长的空地就能保证安全,已知原斜坡AB的前方有6米长的空地,进行这样的改造是否可行?说明理由.
(参考数据:)
24.(2015 繁昌县一模)如图,一堤坝的坡角∠ABC=60°,坡面长度AB=30米(图为横截面),为了使堤坝更加牢固,一施工队欲改变堤坝的坡面,使得坡面的坡角∠ADB=45°,则此时应将坝底向外拓宽多少米?(结果保留到0.1米)(参考数据:≈1.414,≈1.732)
25.(2015 通辽)如图,建筑物AB后有一座假山,其坡度为i=1:,山坡上E点处有一凉亭,测得假山坡脚C与建筑物水平距离BC=25米,与凉亭距离CE=20米,某人从建筑物顶端测得E点的俯角为45°,求建筑物AB的高.(注:坡度i是指坡面的铅直高度与水平宽度的比)
26.(2015 宜宾)如图,某市对位于笔直公路AC上两个小区A、B的供水路线进行优化改造.供水站M在笔直公路AD上,测得供水站M在小区A的南偏东60°方向,在小区B的西南方向,小区A、B之间的距离为300(+l)米,求供水站M分别到小区A、B的距离.(结果可保留根号)
鲁教版九年级数学上册第2单元三角函数的应用同步辅导参考答案
一.选择题(共12小题)
1.C 2.B 3.C 4.C 5.C 6.C 7.C 8.D 9.C
10.D 11.D 12.A
二.填空题(共8小题)
13.25米 14.2 15.(4+4) 16.137 17.(-3)
18. 19.2km 20.
三.解答题(共6小题)
21.解:过C作CE⊥AB于E,设CE=x米,在Rt△AEC中:∠CAE=45°,AE=CE=x
在Rt△BCE中:∠CBE=30°,BE=CE=x,∴x=x+50解之得:x=25+25≈68.30.
答:河宽为68.30米.
(21) (22) (23)
22.解:(1)过M作MN⊥AB,在Rt△AMN中,AM=10,∠MAN=45°,
∴sin∠MAN=,即=,解得:MN=10,
则测速点M到该公路的距离为10米;
(2)由(1)知:AN=MN=10米,
在Rt△MNB中,∠MBN=30°,由tan∠MBN=,得:=,解得:BN=10(米),
∴AB=AN+NB=10+10≈27.3(米),
∴汽车从A到B的平均速度为27.3÷3=9.1(米/秒),
∵9.1米/秒=32.76千米/时<40千米/时,
∴此车没有超速.
23.解:(1)在Rt△ABC中,BC=AC=AB sin45°=(m),
在Rt△ADC中AD==5(m),CD==(m),
∴AD﹣AB≈2.07(m).改善后的斜坡会加长2.07m;
(2)这样改造能行.
∵CD﹣BC≈2.59(m),而6﹣3>2.59,
∴这样改造能行.
24.解:过A点作AE⊥CD于E.在Rt△ABE中,∵∠ABE=60°.
∴AE=AB sin60°=30×=15(米),
BE=AB cos60°=30×=15(米),
在Rt△ADE中,
∵∠ADB=45°,
∴DE=AE=15(米),
∴DB=DE﹣BE=15﹣15≈11.0(米).
故此时应将坝底向外拓宽大约11.0米.
(24) (25) (26)
25.解:过点E作EF⊥BC于点F,过点E作EN⊥AB于点N,
∵建筑物AB后有一座假山,其坡度为i=1:,∴设EF=x,则FC=x,
∵CE=20米,∴x2+(x)2=400,解得:x=10,
则FC=10m,
∵BC=25m,∴BF=NE=(25+10)m,
∴AB=AN+BN=NE+EF=10+25+10=(35+10)m,
答:建筑物AB的高为(35+10)m.
26.B于N,设MN=x米.
在Rt△AMN中,∵∠ANM=90°,∠MAN=30°,
∴MA=2MN=2x,AN=MN=x.
在Rt△AMN中,∵∠BNM=90°,∠MBN=45°,
∴BN=MN=x,MB=MN=x.
∵AN+BN=AB,
∴x+x=300(+l),
∴x=300,
∴MA=2x=600,MB=x=300.
故供水站M到小区A的距离是600米,到小区B的距离是300米.
一.选择题(共12小题)
1.(2015 新泰市二模)如图,为安全起见,萌萌拟加长滑梯,将其倾斜角由45°降至30°.已知滑梯AB的长为3m,点D、B、C在同一水平地面上,那么加长后的滑梯AD的长是( )
A.2 B. 2 C. 3 D. 3m
(1题图) (2题图) (3题图)
2.(2014 随州)如图,要测量B点到河岸AD的距离,在A点测得∠BAD=30°,在C点测得∠BCD=60°,又测得AC=100米,则B点到河岸AD的距离为( )
A.100米 B. 50米 C. 米 D. 50米
3.(2014 白云区校级模拟)如图,两个高度相等的圆柱形水杯,甲杯装满液体,乙杯是空杯.若把甲杯中的液体全部倒入乙杯,则乙杯中的液面与图中点P的距离是( )
A.2cm B. 4cm C. 6cm D. 8cm
4.(2014 山西模拟)如图,沿AB方向开山修路,为了加快施工进度,要在小山的另一边同时施工,从AB上的一点C,取∠ACD=146°,CD=500m,∠D=56°.要使点A,C,E在同一条直线上,那么开挖点E离点D的距离是( )
A.500m B. 500sin56°m C. 500cos56°m D. 500tan56°m
(4题图) (5题图) (6题图)
5.(2015 祁阳县三模)如图,河堤横断面迎水坡AB的坡比是1:,堤高BC=10m,则坡面AB的长度是(
A. 15m B. 20m C. 20m D. 10m
6.如图,一水库大坝的横断面为梯形ABCD,坝顶BC宽6米,坝高20米,斜坡AB的坡度i=1:2.5,斜坡CD的坡角为30度,则坝底AD的长度为( )
A. 56米 B. 66米 C. (56+20)米 D. (50+20)米
7.(2015 衡阳)如图,为了测得电视塔的高度AB,在D处用高为1米的测角仪CD,测得电视塔顶端A的仰角为30°,再向电视塔方向前进100米达到F处,又测得电视塔顶端A的仰角为60°,则这个电视塔的高度AB(单位:米)为( )
A.50 B. 51 C. 50+1 D. 101
8.(2015 南丹县一模)如图,在热气球C处测得地面A、B两点的俯角分别为30°、45°,热气球C的高度CD为100米,点A、D、B在同一直线上,则AB两点的距离是( )
A.200米 B. 200米 C. 220米 D. 米
9.如图,一渔船由西往东航行,在A点测得海岛C位于北偏东60°的方向,前进40海里到达B点,此时,测得海岛C位于北偏东30°的方向,则海里C到航线AB的距离CD是( )
A.20海里 B. 40海里 C. 20海里 D. 40海里
(7题图) (8题图) (9题图)
10.(2015 百色)有一轮船在A处测得南偏东30°方向上有一小岛P,轮船沿正南方向航行至B处,测得小岛P在南偏东45°方向上,按原方向再航行10海里至C处,测得小岛P在正东方向上,则A,B之间的距离是( )海里.
A.10 B. 10﹣10 C. 10 D. 10﹣10
(10题图) (11题图) (12题图) (13题图)
11.(2015 江西校级模拟)数学课外兴趣小组的同学们要测量被池塘相隔的两棵树A、B的距离,他们设计了如图所示的测量方案:从树A沿着垂直于AB的方向走到E,再从E沿着垂直于AE的方向走到F,C为AE上一点,其中3位同学分别测得三组数据:①AC,∠ACB;②EF、DE、AD;③CD,∠ACB,∠ADB.其中能根据所测数据求得A、B两树距离的有( )
A.0组 B. 一组 C. 二组 D. 三组
12.(2015 孝感三模)如图,是意大利著名的比萨斜塔,塔身的中心线与垂直中心线的夹角A约为5゜28′,塔身AB的长为54.5m,则塔顶中心偏离垂直中心线的距离BC是( )
A.54.5×sin5°28′m B. 54.5×cos5°28′m
C.54.5×tan5°28'm D. m
二.填空题(共8小题)
13.(2015 大庆模拟)如图,要测量一段两岸平行的河的宽度,在A点测得∠α=30°,在B点测得∠β=60°,且AB=50米,则这段河岸的宽度为 .
14.(2015 石家庄校级模拟)如图,在坡度为1:3的山坡上种树,要求株距(相邻两树间的水平距离)是6米,则斜坡上相邻两树间的坡面距离是 米(结果保留根号).
15.(2015 永嘉县二模)如图,某广告牌竖直矗立在水平地面上,经测量,得到如下相关数据:CD=2m,∠CAB=30°,∠DBF=45°,AB=10m,则广告牌的高EF= m.(结果保留根号)
16.(2015 荆州)如图,小明在一块平地上测山高,先在B处测得山顶A的仰角为30°,然后向山脚直行100米到达C处,再测得山顶A的仰角为45°,那么山高AD为 米(结果保留整数,测角仪忽略不计,≈1.414,,1.732)
(14题图) (15题图) (16题图)
17.(2015 大连模拟)为了缓解长沙市区内一些主要路段交通拥挤的现状,交警队在一些主要路口设立了交通路况显示牌(如图).已知立杆AB高度是3m,从侧面D点测得显示牌顶端C点和底端B点的仰角分别是60°和45°.则路况显示牌BC的高度为 米.
(17题图) (18题图) (19题图) (20题图)
18.某中学初三年级的学生开展测量物体高度的实践活动,他们要测量一幢建筑物AB的高度.如图,他们先在点C处测得建筑物AB的顶点A的仰角为30°,然后向建筑物AB前进20m到达点D处,又测得点 A的仰角为60°,则建筑物AB的高度是 m.
19.(2015 宁夏)如图,港口A在观测站O的正东方向,OA=4km,某船从港口A出发,沿北偏东15°方向航行一段距离后到达B处,此时从观测站O处测得该船位于北偏东60°的方向,则该船航行的距离(即AB的长)为 .
20.(2015 湖北模拟)一艘观光游船从港口A以北偏东60°的方向出港观光,航行60海里至C处时发生了侧翻沉船事故,立即发出了求救信号,一艘在港口正东方向的海警船接到求救信号,测得事故船在它的北偏东30°方向,马上以40海里每小时的速度前往救援,海警船到达事故船C处所需的时间大约为 小时(用根号表示).
三.解答题(共6小题)
21.(2015 自贡)如图所示,我市某中学课外活动小组的同学利用所学知识去测量釜溪河沙湾段的宽度.小宇同学在A处观测对岸C点,测得∠CAD=45°,小英同学在距A处50米远的B处测得∠CBD=30°,请你根据这些数据算出河宽.(精确到0.01米,参考数据≈1.414,≈1.732)
22.(2015 贺州)根据道路管理规定,在贺州某段笔直公路上行驶的车辆,限速40千米/时,已知交警测速点M到该公路A点的距离为10米,∠MAB=45°,∠MBA=30°(如图所示),现有一辆汽车由A往B方向匀速行驶,测得此车从A点行驶到B点所用的时间为3秒.
(1)求测速点M到该公路的距离;
(2)通过计算判断此车是否超速.(参考数据:≈1.41,≈1.73,≈2.24)
23.(2015 安徽模拟)如图,某滑板爱好者训练时的斜坡示意图,出于安全因素考虑,决定将训练的斜坡的倾角由45°降为30°,已知原斜坡坡面AB的长为5米,点D、B、C在同一水平地面上.
(1)改善后斜坡坡面AD比原斜坡坡面AB会加长多少米?(精确到0.01)
(2)若斜坡的正前方能有3米长的空地就能保证安全,已知原斜坡AB的前方有6米长的空地,进行这样的改造是否可行?说明理由.
(参考数据:)
24.(2015 繁昌县一模)如图,一堤坝的坡角∠ABC=60°,坡面长度AB=30米(图为横截面),为了使堤坝更加牢固,一施工队欲改变堤坝的坡面,使得坡面的坡角∠ADB=45°,则此时应将坝底向外拓宽多少米?(结果保留到0.1米)(参考数据:≈1.414,≈1.732)
25.(2015 通辽)如图,建筑物AB后有一座假山,其坡度为i=1:,山坡上E点处有一凉亭,测得假山坡脚C与建筑物水平距离BC=25米,与凉亭距离CE=20米,某人从建筑物顶端测得E点的俯角为45°,求建筑物AB的高.(注:坡度i是指坡面的铅直高度与水平宽度的比)
26.(2015 宜宾)如图,某市对位于笔直公路AC上两个小区A、B的供水路线进行优化改造.供水站M在笔直公路AD上,测得供水站M在小区A的南偏东60°方向,在小区B的西南方向,小区A、B之间的距离为300(+l)米,求供水站M分别到小区A、B的距离.(结果可保留根号)
鲁教版九年级数学上册第2单元三角函数的应用同步辅导参考答案
一.选择题(共12小题)
1.C 2.B 3.C 4.C 5.C 6.C 7.C 8.D 9.C
10.D 11.D 12.A
二.填空题(共8小题)
13.25米 14.2 15.(4+4) 16.137 17.(-3)
18. 19.2km 20.
三.解答题(共6小题)
21.解:过C作CE⊥AB于E,设CE=x米,在Rt△AEC中:∠CAE=45°,AE=CE=x
在Rt△BCE中:∠CBE=30°,BE=CE=x,∴x=x+50解之得:x=25+25≈68.30.
答:河宽为68.30米.
(21) (22) (23)
22.解:(1)过M作MN⊥AB,在Rt△AMN中,AM=10,∠MAN=45°,
∴sin∠MAN=,即=,解得:MN=10,
则测速点M到该公路的距离为10米;
(2)由(1)知:AN=MN=10米,
在Rt△MNB中,∠MBN=30°,由tan∠MBN=,得:=,解得:BN=10(米),
∴AB=AN+NB=10+10≈27.3(米),
∴汽车从A到B的平均速度为27.3÷3=9.1(米/秒),
∵9.1米/秒=32.76千米/时<40千米/时,
∴此车没有超速.
23.解:(1)在Rt△ABC中,BC=AC=AB sin45°=(m),
在Rt△ADC中AD==5(m),CD==(m),
∴AD﹣AB≈2.07(m).改善后的斜坡会加长2.07m;
(2)这样改造能行.
∵CD﹣BC≈2.59(m),而6﹣3>2.59,
∴这样改造能行.
24.解:过A点作AE⊥CD于E.在Rt△ABE中,∵∠ABE=60°.
∴AE=AB sin60°=30×=15(米),
BE=AB cos60°=30×=15(米),
在Rt△ADE中,
∵∠ADB=45°,
∴DE=AE=15(米),
∴DB=DE﹣BE=15﹣15≈11.0(米).
故此时应将坝底向外拓宽大约11.0米.
(24) (25) (26)
25.解:过点E作EF⊥BC于点F,过点E作EN⊥AB于点N,
∵建筑物AB后有一座假山,其坡度为i=1:,∴设EF=x,则FC=x,
∵CE=20米,∴x2+(x)2=400,解得:x=10,
则FC=10m,
∵BC=25m,∴BF=NE=(25+10)m,
∴AB=AN+BN=NE+EF=10+25+10=(35+10)m,
答:建筑物AB的高为(35+10)m.
26.B于N,设MN=x米.
在Rt△AMN中,∵∠ANM=90°,∠MAN=30°,
∴MA=2MN=2x,AN=MN=x.
在Rt△AMN中,∵∠BNM=90°,∠MBN=45°,
∴BN=MN=x,MB=MN=x.
∵AN+BN=AB,
∴x+x=300(+l),
∴x=300,
∴MA=2x=600,MB=x=300.
故供水站M到小区A的距离是600米,到小区B的距离是300米.
