1.3.1单调性与最大（小）值

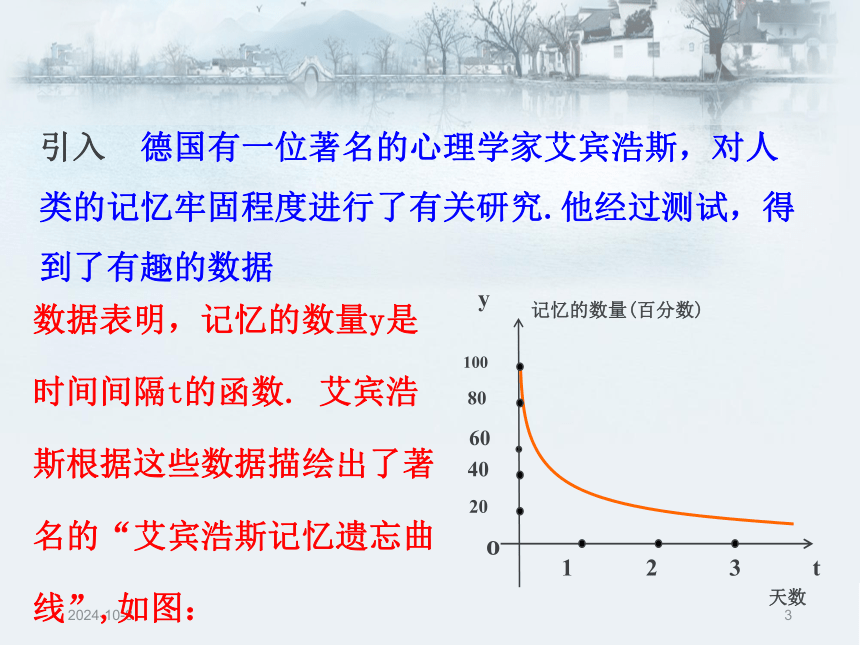
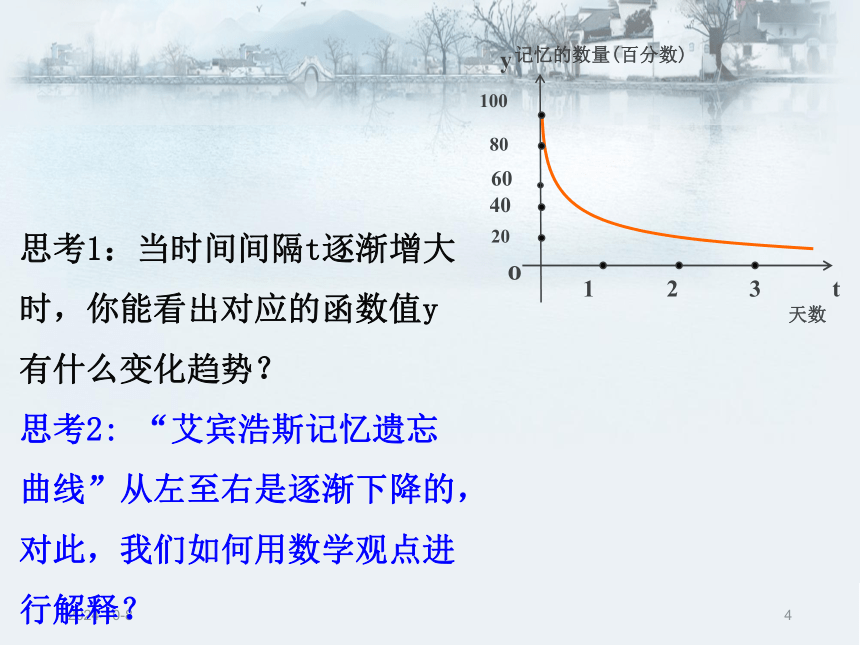
课件47张PPT。2018/12/21喷泉喷出的抛物线型水柱到达“最高点”后便下落，经历了先“增”后“减”的过程，从中我们发现单调性与函数的最值之间似乎有着某种“联系”，让我们来研究——函数的最大值与最小值.2018/12/221.3.1 单调性与 最大（小）值2018/12/23引入 德国有一位著名的心理学家艾宾浩斯，对人类的记忆牢固程度进行了有关研究.他经过测试，得到了有趣的数据数据表明，记忆的数量y是时间间隔t的函数. 艾宾浩斯根据这些数据描绘出了著名的“艾宾浩斯记忆遗忘曲线”,如图：1002018/12/24思考1：当时间间隔t逐渐增大
时，你能看出对应的函数值y
有什么变化趋势？
思考2: “艾宾浩斯记忆遗忘曲线”从左至右是逐渐下降的，对此，我们如何用数学观点进行解释？2018/12/25画出下列函数的图象，观察其变化规律： 1、从左至右图象上升还是下降 ____?
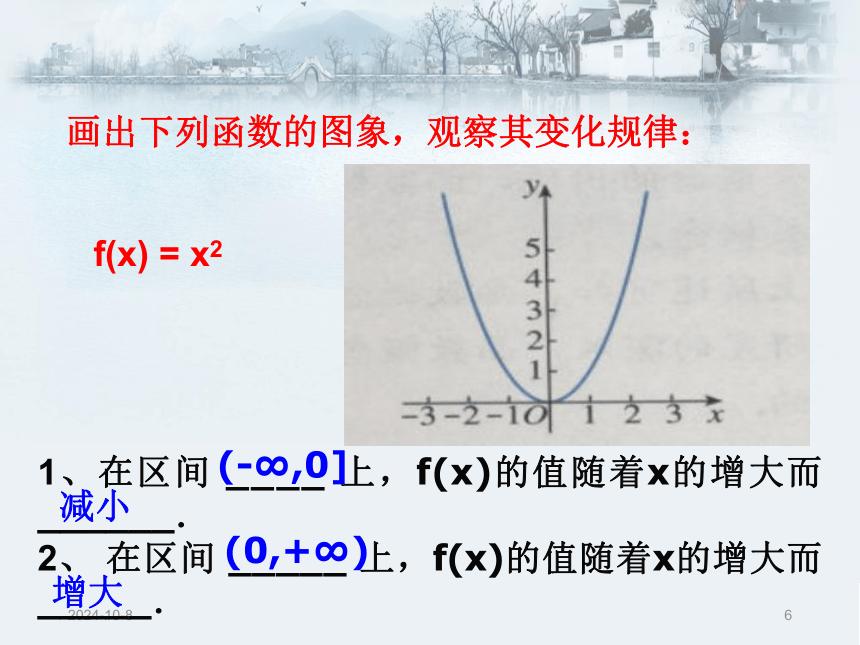
2、在区间 ________上，随着x的增大，f(x)的值随着 ______ ．f(x) = x(-∞,+∞)增大上升2018/12/261、在区间 ____ 上，f(x)的值随着x的增大而 ______．
2、 在区间 _____ 上，f(x)的值随着x的增大而 _____． f(x) = x2(-∞,0](0,+∞)增大减小画出下列函数的图象，观察其变化规律： 2018/12/27在某一区间内
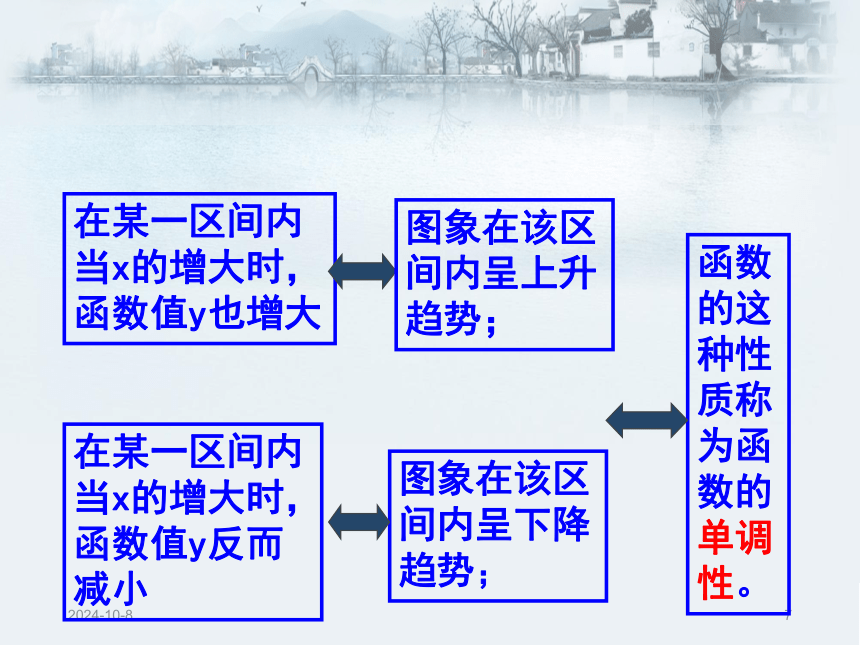
当x的增大时，函数值y反而减小图象在该区间内呈下降趋势；在某一区间内
当x的增大时，函数值y也增大图象在该区间内呈上升趋势；函数的这种性质称为函数的单调性。2018/12/28 如果函数y=f(x)在某个区间上是增函数或是减函数，那么就说函数y=f(x)在这一区间具有（严格的）单调性，
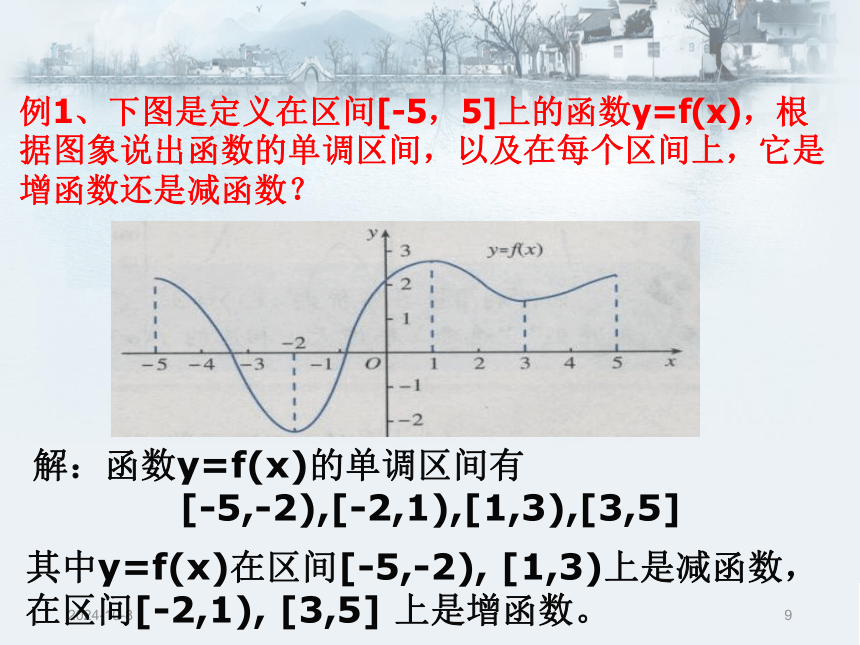
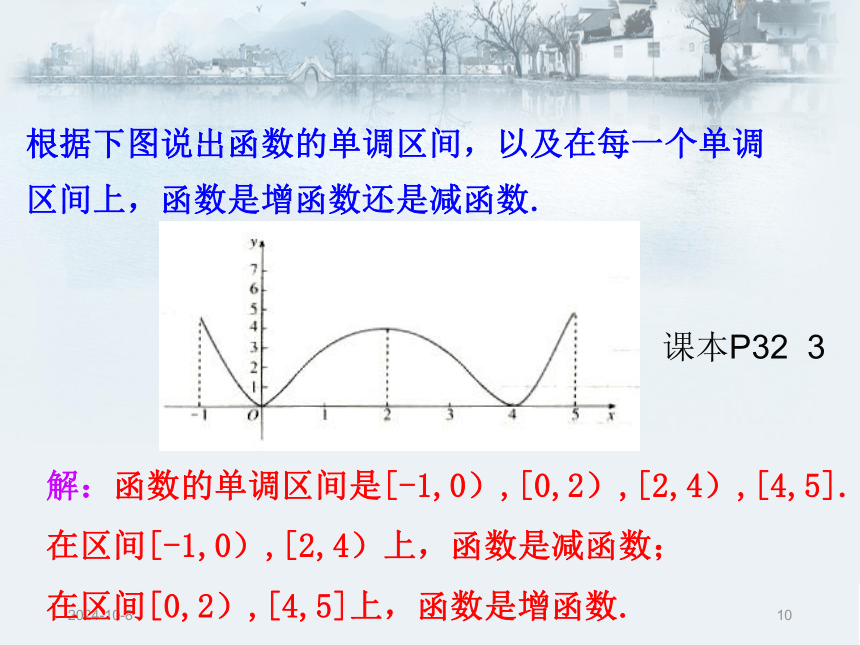
区间D叫做y=f(x)的单调区间. 函数的单调性定义注意：函数的单调区间是其定义域的子集；2018/12/29例1、下图是定义在区间[-5，5]上的函数y=f(x)，根据图象说出函数的单调区间，以及在每个区间上，它是增函数还是减函数？解：函数y=f(x)的单调区间有 [-5,-2),[-2,1),[1,3),[3,5] 其中y=f(x)在区间[-5,-2), [1,3)上是减函数，在区间[-2,1), [3,5] 上是增函数。2018/12/210根据下图说出函数的单调区间，以及在每一个单调区间上，函数是增函数还是减函数.解：函数的单调区间是[-1,0）,[0,2）,[2,4）,[4,5].
在区间[-1,0）,[2,4）上，函数是减函数；
在区间[0,2）,[4,5]上，函数是增函数.课本P32 32018/12/211注意：函数的单调性是对某个区间而言的，对于单独的一点，由于它的函数值是唯一确定的常数，因而没有增减变化，所以不存在单调性问题；对于闭区间上的连续函数来说，只要在开区间上单调，它在闭区间上也就单调，因此，在考虑它的单调区间时，包括不包括端点都可以；2018/12/212DB2018/12/213解：(2)令f(x)＝x2＋2x－3＝(x＋1)2－4.
先作出f(x)的图象，保留其在x轴及x轴上方部分，把它在x轴下方的图象翻到x轴上方就得到y＝|x2＋2x－3|的图象，如图所示．
由图象，易得函数的递增区间是(－3，－1)，(1，＋∞)；
函数的递减区间是(－∞，－3]，(－1,1]．【例1】 求下列函数的单调区间：
(2)f(x)＝|x2＋2x－3|.2018/12/2143．已知函数f(x)＝x2＋2(a－1)x＋2在区间(－∞，4]上是减函数，求实数a的取值范围．
解：f(x)＝x2＋2(a－1)x＋2
＝[x＋(a－1)]2－(a－1)2＋2，
∴此二次函数的对称轴为x＝1－a.
∴f(x)的单调减区间为(－∞，1－a]．2018/12/215∵f(x)在(－∞，4]上是减函数，
∴对称轴x＝1－a必须在直线x＝4的右侧或与其重合．
∴1－a≥4，解得a≤－3.
∴实数a的取值范围为{a|a≤－3}．3．已知函数f(x)＝x2＋2(a－1)x＋2在区间(－∞，4]上是减函数，求实数a的取值范围．2018/12/216?函数 f(x)=x2 :x12x22x0x1x2yf (x1)f (x2)在(0,+∞)上任取 x1、x2 , 2018/12/217如何用x与 f(x)来描述上升的图象？ 如果对于属于定义域I内某个区间上的任意两个称函数 f(x)在这个区间上是增函数。2018/12/218如何用x与 f(x)来描述下降的图象？如果对于属于定义域I内某个区间上的任意两个称函数 f(x)在这个区间上是减函数。2018/12/219 1、函数的单调性是在定义域内的某个区间上的性质，是函数的局部性质；注意： 2 、必须是对于区间D内的任意两个自变量x1，x2；当x1f(x2) 分别是增函数和减函数.2018/12/220在(-∞,0)上是____函数在(0,+∞)上是____函数减减反比例函数 ：-2yOx-11-1122018/12/221在(-∞,0)上是____函数在(0,+∞)上是____函数减减函数 ：yOx 在 (0,+∞) 上任取 x1、 x2
当x1< x2时，都有f(x1) f(x2)>2018/12/222yOx-11-11 取自变量－1< 1，
而 f(－1) f(1)<2018/12/223在
增函数
在
减函数在
增函数
在
减函数在(-∞,+∞)是减函数
在(-∞,0)和(0,+∞)是减函数在(-∞,+∞)是增函数在(-∞,0)和(0,+∞)是增函数2018/12/224证明函数　　　 在R上是减函数.即例2.利用定义：证明：设 是R上任意两个值，且 ，则2018/12/225判断函数单调性的方法步骤 1 任取x1，x2∈D，且x12 作差f(x1)－f(x2)；
3 变形（通常是因式分解和配方）；
4 定号（即判断差f(x1)－f(x2)的正负）；
5 下结论（即指出函数f(x)在给定的区间D上的单调性）． 利用定义证明函数f(x)在给定的区间D上的单调性的一般步骤：2018/12/226D2018/12/2278.已知f(x)是定义在[－1,1]上的增函数，且f(x－1)＜f(1－3x)，求x的取值范围．2018/12/228思考？思考：画出反比例函数f(x)=1/x的图象．P30
1 这个函数的定义域是什么？
2 它在定义域I上的单调性怎样？证明你的结论． 2018/12/229证明：函数f(x)=1/x 在(0，+∞)上是减函数。证明：设x1,x2是(0，+∞)上任意两个实数，且x10,又由x10
所以f(x1)- f(x2)>0, 即f(x1)> f(x2)
因此 f(x)=1/x 在(0，+∞)上是减函数。取值定号变形作差结论2018/12/230课本P39 A 3证明：对于任意的x1，x2∈(－∞，0)且x10，即f(x1)>f(x2)．2018/12/2322018/12/233观察下列两个函数的图象： B探究点1 函数的最大值2018/12/234【解答】第一个函数图象有最高点A,第二个函数图象有最高点B,也就是说,这两个函数的图象都有最高点.
思考2 设函数y=f(x)图象上最高点的纵坐标为M,则对函数定义域内任意自变量x,f(x)与M的大小关系如何?
【解答】 f(x)≤M思考1 这两个函数图象有何共同特征？2018/12/235 最大值 一般地，设函数y=f(x)的定义域为I，如果存在实数M满足： （1）对于任意的x∈I，都有f(x)≤M;
（2）存在x0∈I，使得f(x0) = M那么，称M是函数y=f(x)的最大值 请同学们仿此给出函数最小值的定义2018/12/236最小值 一般地，设函数y=f(x)的定义域为I，如果存在实数M满足： （1）对于任意的x∈I，都有f(x)≥M;
（2）存在x0∈I，使得f(x0) = M那么，称M是函数y=f(x)的最小值 2018/12/2372、函数最大（小）值应该是所有函数值中最大（小）的，即对于任意的x∈I，都有f(x)≤M（f(x)≥M）． 注意：1、函数最大（小）值首先应该是某一个函数值，即存在x0∈I，使得f(x0) = M；2018/12/238-202018/12/2392018/12/240例3、“菊花”烟花是最壮观的烟花之一.制造时一般是期望在它达到最高点时爆裂. 如果在距地面高度h m与时间t s之间的
关系为:h(t)= -4.9t2+14.7t+18 ，
那么烟花冲出后什么时候是
它的爆裂的最佳时刻？这时
距地面的高度是多少（精确
到1m）2018/12/241解：作出函数h(t)= -4.9t2+14.7t+18的图象(如图).显然，函数图象的顶点就是烟花上升的最高点，顶点的横坐标就是烟花爆裂的最佳时刻，纵坐标就是这时距地面的高度. 由于二次函数的知识，对于h(t)=-4.9t2+14.7t+18,我们有: 于是，烟花冲出后1.5秒是它爆裂的最佳时刻,这时距地面的高度为29 m.2018/12/242例4.求函数 在区间[2，6]上的最大值和最小值． 解：设x1,x2是区间[2,6]上的任意两个实数，且x10,(x1-1)(x2-1)>0,于是所以，函数 是区间[2,6]上的减函数.2018/12/243 因此,函数 在区间[2,6]上的两个端点上分别取得最大值和最小值，即在点x=2时取最大值，最大值是2，在x=6时取最小值，最小值为0.4 .2018/12/2442018/12/245利用函数单调性判断函数的最大(小)值的方法 1.利用二次函数的性质（配方法）求函数的最大(小)值 2. 利用图象求函数的最大(小)值 3.利用函数单调性的判断函数的最大(小)值 如果函数y=f(x)在区间[a，b]上单调递增，则函数y=f(x)在x=a处有最小值f(a),在x=b处有最大值f(b) ； 如果函数y=f(x)在区间[a，b]上单调递减，在区间[b，c]上单调递增则函数y=f(x)在x=b处有最小值f(b)； 2018/12/2462018/12/247