北师版七下数学1.4.2单项式与多项式相乘 上课课件(共19张PPT)
文档属性
| 名称 | 北师版七下数学1.4.2单项式与多项式相乘 上课课件(共19张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 5.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-30 11:43:23 | ||
图片预览






文档简介
(共19张PPT)
1.4 整式的乘法
第一章 整式的乘除
第2课时 单项式与多项式相乘
1.能利用数形结合思想,推导单项式乘以多项式法则(难点)
2.能进行单项式与多项式相乘的相关运算(重点)
学习目标
知识储备
1.我们本单元学习整式的乘法,整式包括 式和 式。
单项 多项
2. 什么是多项式?怎么理解多项式的项数和次数?
几个 的和叫做多项式,其中每个 叫做多项式的项,有几个单项式就叫做几项,多项式的次数就是其中次数最高的 的次数。
3.整式的乘法中的单项式乘以单项式法则:
单项式与单项式相乘,把它们的 、 分别相乘,对于只在一个单项式里含有的 ,则连同它的指数 作为积的一个因式。
单项式
单项式
单项式
系数
同底数幂
字母
不变
新课导入
情境引入
狗蛋的后院面积怎么表示
狗蛋种植物的土地是由3块长方形地面构成.如图所示:
根据图中所给的条件你能计算出土地的面积吗?
如果把它看成一个大长方形,那么它的面积可表示为 .
p(a+b+c)
合作探究一:
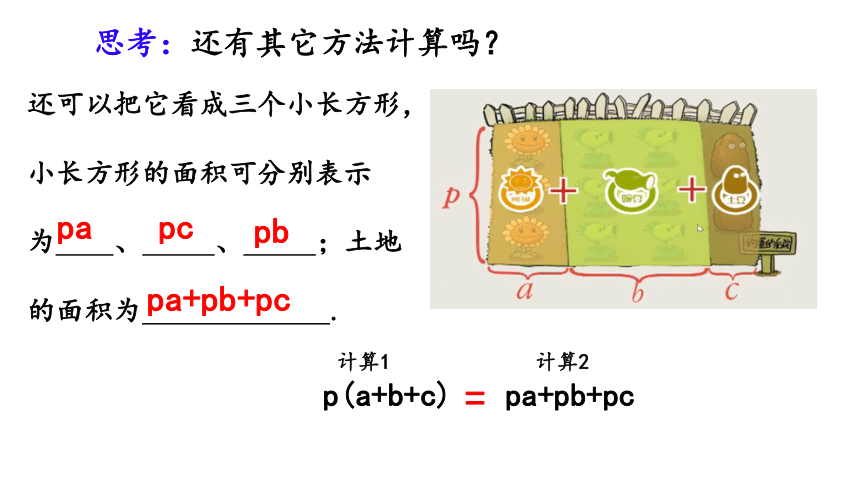
还可以把它看成三个小长方形,小长方形的面积可分别表示为 、 、 ;土地的面积为 .
思考:还有其它方法计算吗?
=
pa+pb+pc
pa
pb
pc
pa+pb+pc
p(a+b+c)
计算1
计算2
p ( a + b)
pb
pa
+
根据乘法的分配律
2a2 ·(3a2+5b) = ?
计算:2a2·(3a2+5b)
合作探究二:
单项式与多项式相乘的法则:
单项式与多项式相乘,就是根据分配律用单项式去乘多项式的每一项,再把所得的积相加.
【要点归纳】
解:原式=2a2·3a2 +2a2· 5b
= 6a4 +10a2b
例1
计算:(1)-4x·(2x2+3x-1) (2)(a3)2·(ac2+bc)
原式=(-4x)·(2x2) + (-4x)·3x + (-4x)·(-1)
=-8x3-12x2+4x
(2)
原式=a6·(ac2+bc)
=a6·ac2+a6·bc
=a7c2 + a6bc
典例精析
解:(1)
计算:
(1)( -2ab)
(2)2(x+y2z+xy2z3)·xyz .
解:
(1)原式=
(2)原式=(2x+2y2z+2xy2z3)·xyz
=2x2yz+2xy3z2+2x2y3z4.
【随堂练习】
例2 先化简,再求值:5a(2a2-5a+3)-2a2(5a+5)+7a2,
其中a=2.
解:5a(2a2-5a+3)-2a2(5a+5)+7a2
原式=10a3-25a2 +15a-10a3-10a2+7a2
=-28a2+15a,
当a=2时,
原式=-28×22+15×2
=-82.
注:单项式与多项式相乘的结果中,应将同类项合并!
1.计算 (1)(x-3y)(-6x) (2)2(x2)3(y2+x2y)
【课中小测】
解:
(1)原式=x(-6x)+(-3y)(-6x)
=-6x2+18xy
(2)原式=2x6(y2+x2y)
=2x6·y2+2x6·x2y
=2x6y2+2x8y
2.化简求值:x(x-1)+2x(x+1)-3x(x-2),其中x=2
原式=x2-x+2x2+2x-3x2+6x
=7x
当x=2时,原式=14.
解:
课堂小结
单项式与多项式相乘的法则:单项式与多项式相乘,就是根据分配律用单项式去乘多项式的每一项,再把所得的积相加.
整式的乘法
单项式乘多项式
实质上是转化为单项式×单项式
注意
(1)计算时,要注意符号问题,多项式中每一项都包括它前面的符号,单项式分别与多项式的每一项相乘时,同号相乘得正,异号相乘得负;
(2)不要出现漏乘现象;
(3)运算要有顺序:先乘方,再乘除,最后加减;
(4)对于混合运算,注意最后应合并同类项;
【达标检测】
(1)单项式与多项式相乘,就是用单项式去乘多项式的
________,再把所得的积________.
(2) 4(a-b+1)=_____________.
每一项
相加
4a-4b+4
(3) 3x(2x-y2)=____________.
6x2-3xy2
(4)(2x-5y+6z)(-3x)=________________.
-6x2+15xy-18xz
(5) (-2a2)2(-a-2b+c)=_________________.
-4a5-8a4b+4a4c
1.填空:
2.计算:
(1)(-2x)·(3x2+x-2);
=-6x3-2x2+4x;
解:原式=(-2x)·(3x2)+(-2x)·x+(-2x)·(-2)
(2)( ab3-2a )· ab.
解:原式= ab3· ab-2a· ab
= a2b4-a2b.
3.计算:-2x2·(xy+y2)-5x(x2y-xy2).
(1)将2x2与5x前面的“-”看成性质符号;
(2)单项式与多项式相乘的结果中,应将同类项合并.
注意
解:原式=( -2x2) ·xy+(-2x2) ·y2+(-5x) ·x2y+(-5x) ·(-xy2)
=-2x3y+(-2x2y2)+(-5x3y)+5x2y2
=-7x3y+3x2y2.
4.先化简,再求值3a(2a2-4a+3)-2a2(3a+4),其中 a=-2.
解:3a(2a2-4a+3)-2a2(3a+4)
=6a3-12a2+9a-6a3-8a2
=-20a2+9a.
当a=-2时,
原式=-20×(-2)2+9×(-2)=-98.
住宅用地
人民广场
商业用地
3a
3a+2b
2a-b
4a
5.如图,一块长方形地用来建造住宅、广场、商厦,
求这块地的面积.
解:4a[(3a+2b)+(2a-b)]
=4a(5a+b)
=4a·5a+4a·b
=20a2+4ab.
答:这块地的面积为20a2+4ab.
1.4 整式的乘法
第一章 整式的乘除
第2课时 单项式与多项式相乘
1.能利用数形结合思想,推导单项式乘以多项式法则(难点)
2.能进行单项式与多项式相乘的相关运算(重点)
学习目标
知识储备
1.我们本单元学习整式的乘法,整式包括 式和 式。
单项 多项
2. 什么是多项式?怎么理解多项式的项数和次数?
几个 的和叫做多项式,其中每个 叫做多项式的项,有几个单项式就叫做几项,多项式的次数就是其中次数最高的 的次数。
3.整式的乘法中的单项式乘以单项式法则:
单项式与单项式相乘,把它们的 、 分别相乘,对于只在一个单项式里含有的 ,则连同它的指数 作为积的一个因式。
单项式
单项式
单项式
系数
同底数幂
字母
不变
新课导入
情境引入
狗蛋的后院面积怎么表示
狗蛋种植物的土地是由3块长方形地面构成.如图所示:
根据图中所给的条件你能计算出土地的面积吗?
如果把它看成一个大长方形,那么它的面积可表示为 .
p(a+b+c)
合作探究一:
还可以把它看成三个小长方形,小长方形的面积可分别表示为 、 、 ;土地的面积为 .
思考:还有其它方法计算吗?
=
pa+pb+pc
pa
pb
pc
pa+pb+pc
p(a+b+c)
计算1
计算2
p ( a + b)
pb
pa
+
根据乘法的分配律
2a2 ·(3a2+5b) = ?
计算:2a2·(3a2+5b)
合作探究二:
单项式与多项式相乘的法则:
单项式与多项式相乘,就是根据分配律用单项式去乘多项式的每一项,再把所得的积相加.
【要点归纳】
解:原式=2a2·3a2 +2a2· 5b
= 6a4 +10a2b
例1
计算:(1)-4x·(2x2+3x-1) (2)(a3)2·(ac2+bc)
原式=(-4x)·(2x2) + (-4x)·3x + (-4x)·(-1)
=-8x3-12x2+4x
(2)
原式=a6·(ac2+bc)
=a6·ac2+a6·bc
=a7c2 + a6bc
典例精析
解:(1)
计算:
(1)( -2ab)
(2)2(x+y2z+xy2z3)·xyz .
解:
(1)原式=
(2)原式=(2x+2y2z+2xy2z3)·xyz
=2x2yz+2xy3z2+2x2y3z4.
【随堂练习】
例2 先化简,再求值:5a(2a2-5a+3)-2a2(5a+5)+7a2,
其中a=2.
解:5a(2a2-5a+3)-2a2(5a+5)+7a2
原式=10a3-25a2 +15a-10a3-10a2+7a2
=-28a2+15a,
当a=2时,
原式=-28×22+15×2
=-82.
注:单项式与多项式相乘的结果中,应将同类项合并!
1.计算 (1)(x-3y)(-6x) (2)2(x2)3(y2+x2y)
【课中小测】
解:
(1)原式=x(-6x)+(-3y)(-6x)
=-6x2+18xy
(2)原式=2x6(y2+x2y)
=2x6·y2+2x6·x2y
=2x6y2+2x8y
2.化简求值:x(x-1)+2x(x+1)-3x(x-2),其中x=2
原式=x2-x+2x2+2x-3x2+6x
=7x
当x=2时,原式=14.
解:
课堂小结
单项式与多项式相乘的法则:单项式与多项式相乘,就是根据分配律用单项式去乘多项式的每一项,再把所得的积相加.
整式的乘法
单项式乘多项式
实质上是转化为单项式×单项式
注意
(1)计算时,要注意符号问题,多项式中每一项都包括它前面的符号,单项式分别与多项式的每一项相乘时,同号相乘得正,异号相乘得负;
(2)不要出现漏乘现象;
(3)运算要有顺序:先乘方,再乘除,最后加减;
(4)对于混合运算,注意最后应合并同类项;
【达标检测】
(1)单项式与多项式相乘,就是用单项式去乘多项式的
________,再把所得的积________.
(2) 4(a-b+1)=_____________.
每一项
相加
4a-4b+4
(3) 3x(2x-y2)=____________.
6x2-3xy2
(4)(2x-5y+6z)(-3x)=________________.
-6x2+15xy-18xz
(5) (-2a2)2(-a-2b+c)=_________________.
-4a5-8a4b+4a4c
1.填空:
2.计算:
(1)(-2x)·(3x2+x-2);
=-6x3-2x2+4x;
解:原式=(-2x)·(3x2)+(-2x)·x+(-2x)·(-2)
(2)( ab3-2a )· ab.
解:原式= ab3· ab-2a· ab
= a2b4-a2b.
3.计算:-2x2·(xy+y2)-5x(x2y-xy2).
(1)将2x2与5x前面的“-”看成性质符号;
(2)单项式与多项式相乘的结果中,应将同类项合并.
注意
解:原式=( -2x2) ·xy+(-2x2) ·y2+(-5x) ·x2y+(-5x) ·(-xy2)
=-2x3y+(-2x2y2)+(-5x3y)+5x2y2
=-7x3y+3x2y2.
4.先化简,再求值3a(2a2-4a+3)-2a2(3a+4),其中 a=-2.
解:3a(2a2-4a+3)-2a2(3a+4)
=6a3-12a2+9a-6a3-8a2
=-20a2+9a.
当a=-2时,
原式=-20×(-2)2+9×(-2)=-98.
住宅用地
人民广场
商业用地
3a
3a+2b
2a-b
4a
5.如图,一块长方形地用来建造住宅、广场、商厦,
求这块地的面积.
解:4a[(3a+2b)+(2a-b)]
=4a(5a+b)
=4a·5a+4a·b
=20a2+4ab.
答:这块地的面积为20a2+4ab.
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
