【五环分层导学-课件】4-12 单元复习 三角形-北师大版数学七(下)
文档属性
| 名称 | 【五环分层导学-课件】4-12 单元复习 三角形-北师大版数学七(下) |

|
|
| 格式 | pptx | ||
| 文件大小 | 16.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-30 00:00:00 | ||
图片预览







文档简介
(共29张PPT)
第四章 三角形
第12课 单元复习
北师大版七年级下册
本套资料以教育部颁布的《数学课程标准(2022)版》为依据,结合新中考改革研究,立足北师大版本教材开发,通过课堂流程的优化设计,内容的层次设计,循序渐进,让不同层次的学生都学有所问,问有所探,探有所获,能力都有不同层次的提高,思维不断生长。
资料简介
【问题1】请举出生活中包含三角形的例子.
【问题2】三角形各边之间及各角之间分别有怎样的关系?
【问题3】举出生活中包含全等图形的例子.
【问题4】举例说明怎样判断两个三角形全等?
【问题5】举例说明三角形全等在生活中的应用.
【问题6】利用尺规,你能用几种方法作一个三角形与已知三角形全等?
【问题7】梳理本章内容,用你喜欢的方式(思维导图、列表等)呈现全章知识结构.完成后请和同学交流,并加以完善.
【例题1】若△ABC中,∠C=70°,∠A=50°,则∠B=%// //%.
【例题2】如图,
①若∠B=30°,∠C=25°,则∠1=%////%度;
②若∠B=20°,∠1=40°,则∠C=%////%度.
60°
55
20
【例题3】在△ABC中,∠A=60°,∠B=∠C,则∠B=%// //%.
【例题4】若三角形的三个内角之比分别为1∶2∶3,则三个内角分别是%// //%、%// //%、%// //%,它是%// //%三角形(锐角、直角、钝角).
【例题5】若等腰三角形的一个角是80°,则另外两个角分别是%// //%.
60°
30°
60°
90°
直角
50°,50°或20°,80°
【例题1】一个三角形的两边长分别是3和8,而第三边长为x,则x的取值范围为%// //%;若第三边长是奇数,那么x=%// //%;若第三边长是偶数,那么x=%// //%.
【例题2】一个等腰三角形一边长9 cm,另一边长4 cm,它的第三条边为%// //%,周长为%// //%.
【例题3】一个等腰三角形一边长9 cm,另一边长5 cm,它的第三条边为%// //%,周长为%// //%.
5<x<11
7或9
6或8或10
9 cm
22 cm
5或9 cm
19或23 cm
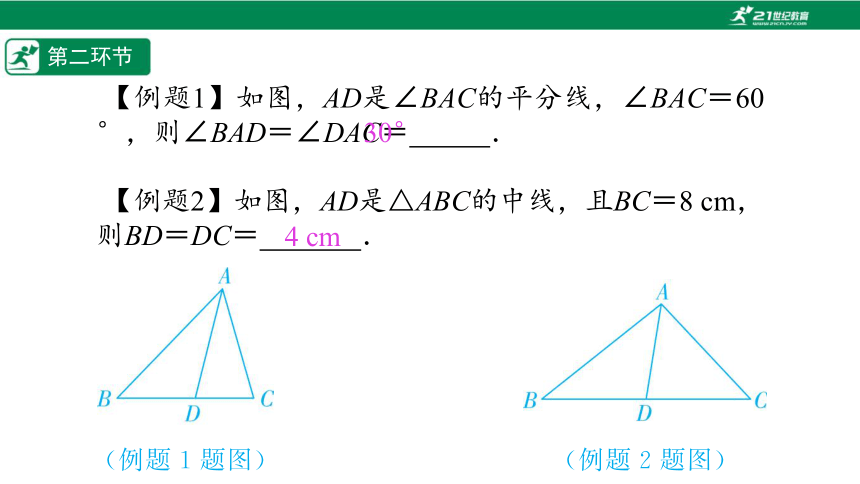
【例题1】如图,AD是∠BAC的平分线,∠BAC=60°,则∠BAD=∠DAC=%// //%.
【例题2】如图,AD是△ABC的中线,且BC=8 cm,则BD=DC=%// //%.
30°
4 cm
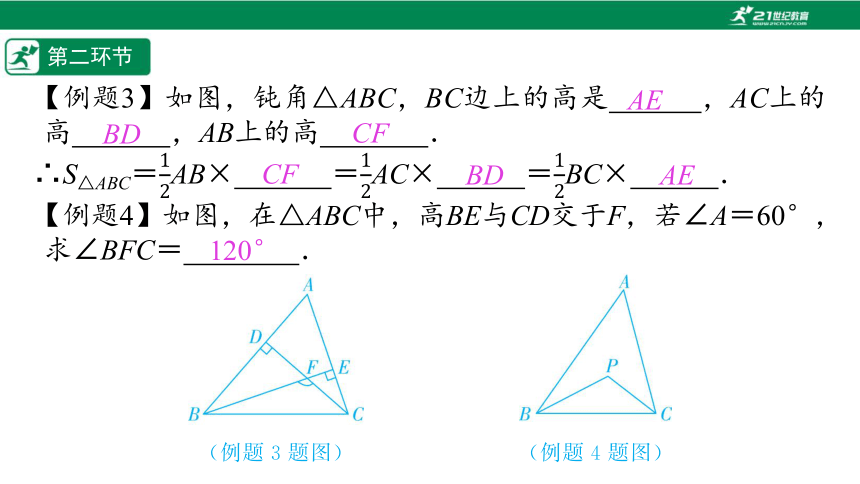
【例题3】如图,钝角△ABC,BC边上的高是%// //%,AC上的高%// //%,AB上的高%// //%.
∴S△ABC=AB×%// //%=AC×%// //%=BC×%// //%.
【例题4】如图,在△ABC中,高BE与CD交于F,若∠A=60°,求∠BFC=%// //%.
AE
BD
CF
CF
BD
AE
120°
【例题5】如图,在△ABC中,AD,AE分别是△ABC的高和角平分线,∠B=30°,∠C=50°,求∠DAE的度数.
解:∵∠BAC+∠B+∠C=180°,
而∠B=30°,∠C=50°,
∴∠BAC=180°-30°-50°=100°,
∵AE是△ABC的角平分线,
∴∠EAC=∠BAC=50°,
又∵AD为高线,
∴∠ADC=90°,而∠C=50°,
∴∠DAC=180°-90°-50°=40°,
∴∠DAE=∠EAC-∠DAC=50°-40°=10°.
【例题1】如图所示,△ACD≌△ABE,则
(1)∠A=%////%,∠ABE=%// //%,∠AEB=%// //%;
(2)AD=%////%,AC=%////%,CD=%////%.
∠A
∠ACD
∠ADC
AE
AB
BE
【例题1】如图,D、E分别是AB,AC上一点,若∠B=∠C,则在下列条件中,无法判定△ABE≌△ACD是(%////%)
A.AD=AE
B.AB=AC
C.BE=CD
D.∠AEB=∠ADC
D
【例题2】如图,已知AD为△ABC中BC边上的中线,CE∥AB交AD的延长线于E.求证:AB=CE.
证明:∵AD为BC的中线,∴BD=CD.
∵CE//AB,∴∠BAD=∠CED.
在△ABD与△ECD中,,
∴△ABD≌△ECD(AAS),∴AB=EC.
【例题3】已知如图,AB=AD,AC=AE,∠1=∠2,试猜想∠1与∠3的大小关系,并证明你的结论.
解:猜想:∠1=∠3,∵∠1=∠2,
∴∠1+∠DAE=∠2+∠DAE,即∠BAE=∠DAC,
在△BAE与△DAC中,,
∴△BAE≌△DAC(SAS),∴∠B=∠D,
∵∠AMB=∠DMN,
∠1=180°-∠B-∠AMB,∠3=180°-∠D-∠DMN,
∴∠1=∠3.
【例题1】小红家有一个小口瓶(如图所示),她很想知道它的内径是多少?但是尺子不能伸到里边直接测,于是她拿来了两根长度相同的细木条,并且把两根细木条的中点固定在一起,木条可以绕中点转动,这样只要量出AB的长,就可以知道玻璃瓶的内径是多少,那么△OAB≌△OCD理由是(%////%)
A.边角边 B.角边角
C.边边边 D.角角边
A
对点练习:如图,在△ABC中,∠BAC是钝角,AD⊥BC、EB⊥BC、FC⊥BC,(%////%)
A.AD是△ABC的高
B.EB是△ABC的高
C.FC是△ABC的高
D.AE、AF是△ABC的高
A
对点练习:在下列各组条件中不能说明△ABC≌△DEF的是(%////%)
A.AC=DF,BC=EF,∠A=∠D
B.AB=DE,∠B=∠E,∠C=∠F
C.AB=DE,∠A=∠D,∠B=∠E
D.AB=DE,BC=EF,AC=DF
A
对点练习:如图,△ABC≌△CDA,并且BC=DA,那么下列结论错误的是(%////%)
A.∠1=∠2 B.AC=CA
C.AB=AD D.∠B=∠D
C
1.如图,△ABC≌△BAD,A和B,C和D分别是对应顶点,若AB=6 cm,AC=4 cm,BC=5 cm,则AD的长为(%////%)
A.4 cm B.5 cm
C.6 cm D.以上都不对
B
2.下列说法正确的是(%////%)
A.周长相等的两个三角形全等
B.有两边和其中一边的对角对应相等的两个三角形全等
C.面积相等的两个三角形全等
D.有两个角和其中一角的对边对应相等的两个三角形全等
D
3.在△ABC中,∠B=∠C,与△ABC全等的三角形有一个角是100°,那么在△ABC中,与这100°角对应相等的角是(%////%)
A.∠A B.∠B C.∠C D.∠B或∠C
A
4.下列条件中,能判定△ABC≌△DEF的是(%////%)
A.AB=DE,BC=ED,∠A=∠D
B.∠A=∠D,∠C=∠F,AC=EF
C.∠B=∠E,∠A=∠D,AC=EF
D.∠B=∠E,∠A=∠D,AB=DE
D
5. AD是△ABC中BC边上的中线,若AB=4,AC=6,则AD的取值范围是(%////%)
A.AD>1 B.AD<5
C.1<AD<5 D.2<AD<10
C
6.下列命题错误的是(%////%)
A.两条直角边对应相等的两个直角三角形全等
B.一条边和一个角对应相等的两个直角三角形全等
C.有两边和其中一边的对角(此角为钝角)对应相等的两个三角形全等
D.有两条边对应相等的两个直角三角形全等
B
7.如图,在△ABC中,AB=AC,BD⊥AC于D,CE⊥AB于E,BD和CE交于O,AO的延长线交BC于F,则图中全等的三角形有(%////%)
A.3对 B.4对
C.5对 D.7对
D
8.如图,要测量水池宽AB,可从点A出发在地面上画一条线段AC,使AC⊥AB,再从点C观测,在BA的延长线上测得一点D,使∠ACD=∠ACB,这时量得AD=120 m,则水池宽AB的长度是%// //% m.
120
9.如图,△ABN≌△ACM,∠B和∠C是对应角,AB与AC是对应边,写出其他对应边和对应角.
解:∵△ABN≌△ACM,∠B和∠C是对应角,AB与AC是对应边,
∴对应边:AN与AM,BN与CM;
对应角:∠BAN=∠CAM,∠ANB=∠AMC .
10.如图,已知AC⊥AB,DB⊥AB,AC=BE,AE=BD,试猜想线段CE与DE的大小与位置关系,并证明你的结论.
解:CE=ED,CE⊥DE,理由如下:
∵AC⊥AB,DB⊥AB,AC=BE,AE=BD,
∴△CAE≌△EBD.
∴∠CEA=∠D,CE=ED.
∵∠D+∠DEB=90°,
∴∠CEA+∠DEB=90°.
即线段CE与DE的大小与位置关系为相等且垂直.
11.(★)已知如图,E、F在BD上,且AB=CD,BF=DE,AE=CF,求证:AC与BD互相平分.
证明:∵BF=DE,∴BF-EF=DE-EF,即BE=DF,
在△ABE和△DFC中,,
∴△ABE≌△CDF(SSS),∴∠B=∠D.
在△ABO和△CDO中,,
∴△ABO≌△CDO(AAS),∴AO=CO,BO=DO,
即AC与BD互相平分.
12.如图,∠ABC=90°,AB=BC,D为AC上一点,分别过A、C作BD的垂线,垂足分别为E,F,求证:EF=CF-AE.
证明:∵过A、C作BD的垂线,垂足分别为E,F,
∴∠E=∠BFC=90°,
∵∠ABC=90°,
∴∠EAB+∠ABE=90°,∠FBC+∠ABE=90°,
∴∠EAB=∠FBC,
在△AEB和△BFC中,,
∴△AEB≌△BFC(AAS),
∴AE=BF,BE=CF,∴EF=BE-BF=CF-AE.
第四章 三角形
第12课 单元复习
北师大版七年级下册
本套资料以教育部颁布的《数学课程标准(2022)版》为依据,结合新中考改革研究,立足北师大版本教材开发,通过课堂流程的优化设计,内容的层次设计,循序渐进,让不同层次的学生都学有所问,问有所探,探有所获,能力都有不同层次的提高,思维不断生长。
资料简介
【问题1】请举出生活中包含三角形的例子.
【问题2】三角形各边之间及各角之间分别有怎样的关系?
【问题3】举出生活中包含全等图形的例子.
【问题4】举例说明怎样判断两个三角形全等?
【问题5】举例说明三角形全等在生活中的应用.
【问题6】利用尺规,你能用几种方法作一个三角形与已知三角形全等?
【问题7】梳理本章内容,用你喜欢的方式(思维导图、列表等)呈现全章知识结构.完成后请和同学交流,并加以完善.
【例题1】若△ABC中,∠C=70°,∠A=50°,则∠B=%// //%.
【例题2】如图,
①若∠B=30°,∠C=25°,则∠1=%////%度;
②若∠B=20°,∠1=40°,则∠C=%////%度.
60°
55
20
【例题3】在△ABC中,∠A=60°,∠B=∠C,则∠B=%// //%.
【例题4】若三角形的三个内角之比分别为1∶2∶3,则三个内角分别是%// //%、%// //%、%// //%,它是%// //%三角形(锐角、直角、钝角).
【例题5】若等腰三角形的一个角是80°,则另外两个角分别是%// //%.
60°
30°
60°
90°
直角
50°,50°或20°,80°
【例题1】一个三角形的两边长分别是3和8,而第三边长为x,则x的取值范围为%// //%;若第三边长是奇数,那么x=%// //%;若第三边长是偶数,那么x=%// //%.
【例题2】一个等腰三角形一边长9 cm,另一边长4 cm,它的第三条边为%// //%,周长为%// //%.
【例题3】一个等腰三角形一边长9 cm,另一边长5 cm,它的第三条边为%// //%,周长为%// //%.
5<x<11
7或9
6或8或10
9 cm
22 cm
5或9 cm
19或23 cm
【例题1】如图,AD是∠BAC的平分线,∠BAC=60°,则∠BAD=∠DAC=%// //%.
【例题2】如图,AD是△ABC的中线,且BC=8 cm,则BD=DC=%// //%.
30°
4 cm
【例题3】如图,钝角△ABC,BC边上的高是%// //%,AC上的高%// //%,AB上的高%// //%.
∴S△ABC=AB×%// //%=AC×%// //%=BC×%// //%.
【例题4】如图,在△ABC中,高BE与CD交于F,若∠A=60°,求∠BFC=%// //%.
AE
BD
CF
CF
BD
AE
120°
【例题5】如图,在△ABC中,AD,AE分别是△ABC的高和角平分线,∠B=30°,∠C=50°,求∠DAE的度数.
解:∵∠BAC+∠B+∠C=180°,
而∠B=30°,∠C=50°,
∴∠BAC=180°-30°-50°=100°,
∵AE是△ABC的角平分线,
∴∠EAC=∠BAC=50°,
又∵AD为高线,
∴∠ADC=90°,而∠C=50°,
∴∠DAC=180°-90°-50°=40°,
∴∠DAE=∠EAC-∠DAC=50°-40°=10°.
【例题1】如图所示,△ACD≌△ABE,则
(1)∠A=%////%,∠ABE=%// //%,∠AEB=%// //%;
(2)AD=%////%,AC=%////%,CD=%////%.
∠A
∠ACD
∠ADC
AE
AB
BE
【例题1】如图,D、E分别是AB,AC上一点,若∠B=∠C,则在下列条件中,无法判定△ABE≌△ACD是(%////%)
A.AD=AE
B.AB=AC
C.BE=CD
D.∠AEB=∠ADC
D
【例题2】如图,已知AD为△ABC中BC边上的中线,CE∥AB交AD的延长线于E.求证:AB=CE.
证明:∵AD为BC的中线,∴BD=CD.
∵CE//AB,∴∠BAD=∠CED.
在△ABD与△ECD中,,
∴△ABD≌△ECD(AAS),∴AB=EC.
【例题3】已知如图,AB=AD,AC=AE,∠1=∠2,试猜想∠1与∠3的大小关系,并证明你的结论.
解:猜想:∠1=∠3,∵∠1=∠2,
∴∠1+∠DAE=∠2+∠DAE,即∠BAE=∠DAC,
在△BAE与△DAC中,,
∴△BAE≌△DAC(SAS),∴∠B=∠D,
∵∠AMB=∠DMN,
∠1=180°-∠B-∠AMB,∠3=180°-∠D-∠DMN,
∴∠1=∠3.
【例题1】小红家有一个小口瓶(如图所示),她很想知道它的内径是多少?但是尺子不能伸到里边直接测,于是她拿来了两根长度相同的细木条,并且把两根细木条的中点固定在一起,木条可以绕中点转动,这样只要量出AB的长,就可以知道玻璃瓶的内径是多少,那么△OAB≌△OCD理由是(%////%)
A.边角边 B.角边角
C.边边边 D.角角边
A
对点练习:如图,在△ABC中,∠BAC是钝角,AD⊥BC、EB⊥BC、FC⊥BC,(%////%)
A.AD是△ABC的高
B.EB是△ABC的高
C.FC是△ABC的高
D.AE、AF是△ABC的高
A
对点练习:在下列各组条件中不能说明△ABC≌△DEF的是(%////%)
A.AC=DF,BC=EF,∠A=∠D
B.AB=DE,∠B=∠E,∠C=∠F
C.AB=DE,∠A=∠D,∠B=∠E
D.AB=DE,BC=EF,AC=DF
A
对点练习:如图,△ABC≌△CDA,并且BC=DA,那么下列结论错误的是(%////%)
A.∠1=∠2 B.AC=CA
C.AB=AD D.∠B=∠D
C
1.如图,△ABC≌△BAD,A和B,C和D分别是对应顶点,若AB=6 cm,AC=4 cm,BC=5 cm,则AD的长为(%////%)
A.4 cm B.5 cm
C.6 cm D.以上都不对
B
2.下列说法正确的是(%////%)
A.周长相等的两个三角形全等
B.有两边和其中一边的对角对应相等的两个三角形全等
C.面积相等的两个三角形全等
D.有两个角和其中一角的对边对应相等的两个三角形全等
D
3.在△ABC中,∠B=∠C,与△ABC全等的三角形有一个角是100°,那么在△ABC中,与这100°角对应相等的角是(%////%)
A.∠A B.∠B C.∠C D.∠B或∠C
A
4.下列条件中,能判定△ABC≌△DEF的是(%////%)
A.AB=DE,BC=ED,∠A=∠D
B.∠A=∠D,∠C=∠F,AC=EF
C.∠B=∠E,∠A=∠D,AC=EF
D.∠B=∠E,∠A=∠D,AB=DE
D
5. AD是△ABC中BC边上的中线,若AB=4,AC=6,则AD的取值范围是(%////%)
A.AD>1 B.AD<5
C.1<AD<5 D.2<AD<10
C
6.下列命题错误的是(%////%)
A.两条直角边对应相等的两个直角三角形全等
B.一条边和一个角对应相等的两个直角三角形全等
C.有两边和其中一边的对角(此角为钝角)对应相等的两个三角形全等
D.有两条边对应相等的两个直角三角形全等
B
7.如图,在△ABC中,AB=AC,BD⊥AC于D,CE⊥AB于E,BD和CE交于O,AO的延长线交BC于F,则图中全等的三角形有(%////%)
A.3对 B.4对
C.5对 D.7对
D
8.如图,要测量水池宽AB,可从点A出发在地面上画一条线段AC,使AC⊥AB,再从点C观测,在BA的延长线上测得一点D,使∠ACD=∠ACB,这时量得AD=120 m,则水池宽AB的长度是%// //% m.
120
9.如图,△ABN≌△ACM,∠B和∠C是对应角,AB与AC是对应边,写出其他对应边和对应角.
解:∵△ABN≌△ACM,∠B和∠C是对应角,AB与AC是对应边,
∴对应边:AN与AM,BN与CM;
对应角:∠BAN=∠CAM,∠ANB=∠AMC .
10.如图,已知AC⊥AB,DB⊥AB,AC=BE,AE=BD,试猜想线段CE与DE的大小与位置关系,并证明你的结论.
解:CE=ED,CE⊥DE,理由如下:
∵AC⊥AB,DB⊥AB,AC=BE,AE=BD,
∴△CAE≌△EBD.
∴∠CEA=∠D,CE=ED.
∵∠D+∠DEB=90°,
∴∠CEA+∠DEB=90°.
即线段CE与DE的大小与位置关系为相等且垂直.
11.(★)已知如图,E、F在BD上,且AB=CD,BF=DE,AE=CF,求证:AC与BD互相平分.
证明:∵BF=DE,∴BF-EF=DE-EF,即BE=DF,
在△ABE和△DFC中,,
∴△ABE≌△CDF(SSS),∴∠B=∠D.
在△ABO和△CDO中,,
∴△ABO≌△CDO(AAS),∴AO=CO,BO=DO,
即AC与BD互相平分.
12.如图,∠ABC=90°,AB=BC,D为AC上一点,分别过A、C作BD的垂线,垂足分别为E,F,求证:EF=CF-AE.
证明:∵过A、C作BD的垂线,垂足分别为E,F,
∴∠E=∠BFC=90°,
∵∠ABC=90°,
∴∠EAB+∠ABE=90°,∠FBC+∠ABE=90°,
∴∠EAB=∠FBC,
在△AEB和△BFC中,,
∴△AEB≌△BFC(AAS),
∴AE=BF,BE=CF,∴EF=BE-BF=CF-AE.
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
