【五环分层导学-课件】6-2 频率的稳定性-北师大版数学七(下)
文档属性
| 名称 | 【五环分层导学-课件】6-2 频率的稳定性-北师大版数学七(下) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-30 00:00:00 | ||
图片预览





文档简介
(共18张PPT)
第六章 概率初步
第2课 频率的稳定性
北师大版七年级下册
本套资料以教育部颁布的《数学课程标准(2022)版》为依据,结合新中考改革研究,立足北师大版本教材开发,通过课堂流程的优化设计,内容的层次设计,循序渐进,让不同层次的学生都学有所问,问有所探,探有所获,能力都有不同层次的提高,思维不断生长。
新授课通过激活思维、探究新知、双基巩固、综合运用、分层反馈等环节来完成。
资料简介
(1)同桌两人做20次掷硬币的游戏,数据如下:
在n次重复试验中,事件A发生了m次,则比值称为事件A发生的%// //%.
试验总次数 20
正面朝上的次数
正面朝下的次数
正面朝上的频率
正面朝下的频率
频率
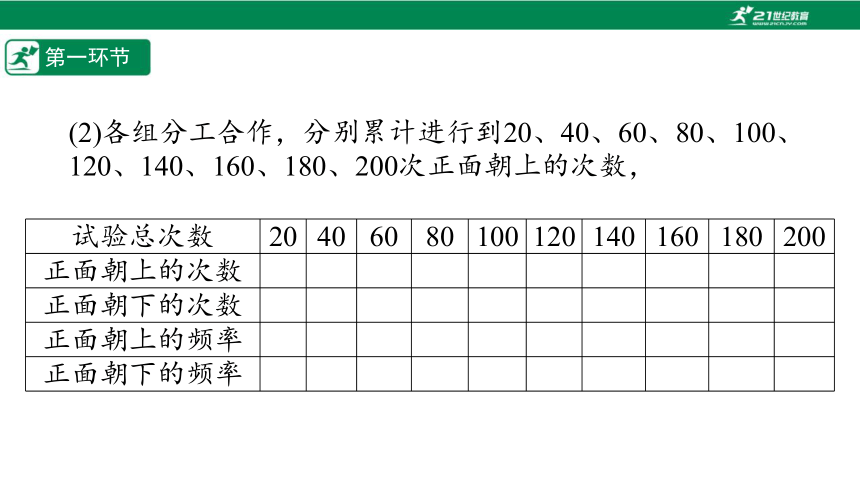
(2)各组分工合作,分别累计进行到20、40、60、80、100、120、140、160、180、200次正面朝上的次数,
试验总次数 20 40 60 80 100 120 140 160 180 200
正面朝上的次数
正面朝下的次数
正面朝上的频率
正面朝下的频率
(3)根据上表,完成下图的折线统计图:
观察折线统计图,你发现了什么规律?
答:当试验次数较小时,折线上下摆动的幅度可能比较大;但当试验次数很大时,无论是正面朝上的频率还是正面朝下的频率,都会稳定在常数()的附近.也就是说,事件发生的频率具有稳定性,并且正面朝上的频率和正面朝下的频率稳定的值相等,它们发生的可能性大致相等.
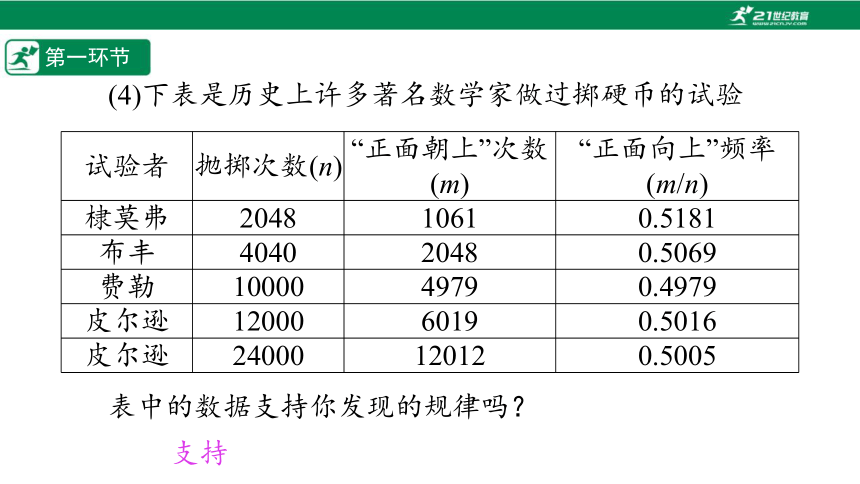
(4)下表是历史上许多著名数学家做过掷硬币的试验
试验者 抛掷次数(n) “正面朝上”次数(m) “正面向上”频率(m/n)
棣莫弗 2048 1061 0.5181
布丰 4040 2048 0.5069
费勒 10000 4979 0.4979
皮尔逊 12000 6019 0.5016
皮尔逊 24000 12012 0.5005
表中的数据支持你发现的规律吗?
支持
小结:(1)无论是掷质地均匀的硬币还是掷图钉,在试验次数很大时正面朝上(针尖朝上)的%//频率//%都会在一个%//常数//%附近摆动,这就是%//频率//%的%//稳定性//%.
(2)用这个常数来表示事件A发生的可能性的大小,把刻画事件A发生的可能性大小的数值,称为事件A发生的%//概率//%,记为%//P(A)//%.
(3)一般地,常用随机事件A发生的%//频率//%来估算事件A发生的%//概率//%.
P(必然事件)=%//1//% P(不可能事件)=%//0//%
随机事件发生的概率P(A)为%//0//%与%//1//%之间的一个常数.
小结:(1)无论是掷质地均匀的硬币还是掷图钉,在试验次数很大时正面朝上(针尖朝上)的%//频率//%都会在一个%//常数//%附近摆动,这就是%//频率//%的%//稳定性//%.
(2)用这个常数来表示事件A发生的可能性的大小,把刻画事件A发生的可能性大小的数值,称为事件A发生的%//概率//%,记为%//P(A)//%.
(3)一般地,常用随机事件A发生的%//频率//%来估算事件A发生的%//概率//%.
P(必然事件)=%//1//% P(不可能事件)=%//0//%
随机事件发生的概率P(A)为%//0//%与%//1//%之间的一个常数.
【例题1】(1)小凡做了5次掷均匀硬币的试验,其中有3次正面朝上,2次正面朝下,因此他认为正面朝上的概率大约为,朝下的概率约为,你同意他的观点吗?你认为他再多做一些试验,结果还是这样吗?
解:不同意他的观点,理由如下:
他再掷一次,正面有可能朝上,反面也有可能朝上,各占,如果小明进行大量的掷质地均匀硬币的试验则正面朝上和正面朝下的的概率会稳定在的附近.
(2)掷一枚质地均匀的硬币,正面朝上的概率为,那么,掷100次硬币,你能保证恰好50次正面朝上吗?为什么?
/答:不能保证.因为概率是针对大量试验而言的,大量试验中所存在的规律并不在一次试验中存在,正面朝上概率是,不能保证2次试验中恰好发生1次,也不能保证在100次试验中恰好发生50次,只是当试验的次数越来越大时,正面朝上的概率会稳定到.
【例题2】(★)在一个不透明的口袋里装有只有颜色不同的黑、白两种颜色的球共30只,某小组做摸球实验,将球搅匀后从中随机摸出一个球记下颜色,再把它放回袋中,不断重复.下表是活动进行中的一组统计数据:
(1)请估计:当n很大时,摸到白球的频率将会接近%// //%;
(2)假如你去摸一次,你摸到白球的概率是%// //%,摸到黑球的概率是%// //%;
(3)试估算口袋中黑、白两种颜色的球各有多少只?
摸球的次数n 100 150 200 500 800 1000 …
摸到白球的次数m 58 96 116 295 484 601 …
摸到白球的频率 0.58 0.64 0.58 0.59 0.605 0.601 …
0.6
0.6
0.4
解:(3)因为摸到白球的概率是0.6,摸到黑球的概率是0.4,所以口袋中黑、白两种颜色的球:白球是30×0.6=18个,黑球是30×0.4=12个.
1.在一个布袋中装有红、白两种颜色的小球,它们除颜色外没有任何其他区别.其中红球若干,白球5个,袋中的球已搅匀.若从袋中随机取出1个球,取出红球的可能性大,则红球的个数是(%////%)
A.4个 B.5 C.不足4个 D.6个或6个以上
D
2.下列事件发生的可能性为0的是(%////%)
A.掷两枚骰子,同时出现数字“6”朝上
B.小明从家里到学校用了10分钟,从学校回到家里却用了15分钟
C.今天是星期天,昨天必定是星期六
D.小明步行的速度是每小时50千米
D
3.关于频率和概率的关系,下列说法正确的是(%////%)
A.频率等于概率
B.当实验次数很大时,频率稳定在概率附近
C.当实验次数很大时,概率稳定在频率附近
D.实验得到的频率与概率不可能相等
B
4.小明做了5次掷质地均匀硬币的试验,其中有2次正面朝上、3次正面朝下.他认为再掷一次,一定正面朝上.你同意他的观点吗?与同伴进行交流.
解:不同意他的观点,理由如下:
他再掷一次,正面有可能朝上,反面也有可能朝上,各占,如果小明进行大量的掷质地均匀硬币的试验则正面朝上的概率为.
5.某位篮球运动员在同样的条件下进行投篮练习,结果如下表:
(1)将上表补充完整;
(2)这位运动员投篮一次,进球的概率约是多少?
(3)若这位运动员投篮10次,必定会投进8次吗?为什么?
投篮次数(n) 8 10 15 20 30 40 50
进球次数(m) 6 8 12 17 25 32 38
进球频率()
解:(1)答案为:0.75;0.8;0.8;0.85;0.83;0.8;0.76;
(2)这位运动员投篮一次,进球的概率约是0.8;
(3)若这位运动员投篮10次,不一定会投进8次.
因为进球的概率是0.8是通过大量重复实验得到的,而投篮10次是随机的,所以不一定会投进8次,可能都不进,也可能都进.
6.(★)掷一枚质地均匀的骰子.
(1)会出现哪些可能的结果?
(2)掷出的点数为1与掷出的点数为2的可能性相同吗?掷出的点数为1与掷出的点数为3的可能性相同吗?
(3)每种结果出现的可能性相同吗?你是怎样做的?
解:(1)会出现1,2,3,4,5,6,一共六种可能的结果;
(2)掷出的点数为1与掷出的点数为2的可能性相同;掷出的点数为1与掷出的点数为3的可能性相同;
(3)1÷6.故每种结果出现的可能性相同.
第六章 概率初步
第2课 频率的稳定性
北师大版七年级下册
本套资料以教育部颁布的《数学课程标准(2022)版》为依据,结合新中考改革研究,立足北师大版本教材开发,通过课堂流程的优化设计,内容的层次设计,循序渐进,让不同层次的学生都学有所问,问有所探,探有所获,能力都有不同层次的提高,思维不断生长。
新授课通过激活思维、探究新知、双基巩固、综合运用、分层反馈等环节来完成。
资料简介
(1)同桌两人做20次掷硬币的游戏,数据如下:
在n次重复试验中,事件A发生了m次,则比值称为事件A发生的%// //%.
试验总次数 20
正面朝上的次数
正面朝下的次数
正面朝上的频率
正面朝下的频率
频率
(2)各组分工合作,分别累计进行到20、40、60、80、100、120、140、160、180、200次正面朝上的次数,
试验总次数 20 40 60 80 100 120 140 160 180 200
正面朝上的次数
正面朝下的次数
正面朝上的频率
正面朝下的频率
(3)根据上表,完成下图的折线统计图:
观察折线统计图,你发现了什么规律?
答:当试验次数较小时,折线上下摆动的幅度可能比较大;但当试验次数很大时,无论是正面朝上的频率还是正面朝下的频率,都会稳定在常数()的附近.也就是说,事件发生的频率具有稳定性,并且正面朝上的频率和正面朝下的频率稳定的值相等,它们发生的可能性大致相等.
(4)下表是历史上许多著名数学家做过掷硬币的试验
试验者 抛掷次数(n) “正面朝上”次数(m) “正面向上”频率(m/n)
棣莫弗 2048 1061 0.5181
布丰 4040 2048 0.5069
费勒 10000 4979 0.4979
皮尔逊 12000 6019 0.5016
皮尔逊 24000 12012 0.5005
表中的数据支持你发现的规律吗?
支持
小结:(1)无论是掷质地均匀的硬币还是掷图钉,在试验次数很大时正面朝上(针尖朝上)的%//频率//%都会在一个%//常数//%附近摆动,这就是%//频率//%的%//稳定性//%.
(2)用这个常数来表示事件A发生的可能性的大小,把刻画事件A发生的可能性大小的数值,称为事件A发生的%//概率//%,记为%//P(A)//%.
(3)一般地,常用随机事件A发生的%//频率//%来估算事件A发生的%//概率//%.
P(必然事件)=%//1//% P(不可能事件)=%//0//%
随机事件发生的概率P(A)为%//0//%与%//1//%之间的一个常数.
小结:(1)无论是掷质地均匀的硬币还是掷图钉,在试验次数很大时正面朝上(针尖朝上)的%//频率//%都会在一个%//常数//%附近摆动,这就是%//频率//%的%//稳定性//%.
(2)用这个常数来表示事件A发生的可能性的大小,把刻画事件A发生的可能性大小的数值,称为事件A发生的%//概率//%,记为%//P(A)//%.
(3)一般地,常用随机事件A发生的%//频率//%来估算事件A发生的%//概率//%.
P(必然事件)=%//1//% P(不可能事件)=%//0//%
随机事件发生的概率P(A)为%//0//%与%//1//%之间的一个常数.
【例题1】(1)小凡做了5次掷均匀硬币的试验,其中有3次正面朝上,2次正面朝下,因此他认为正面朝上的概率大约为,朝下的概率约为,你同意他的观点吗?你认为他再多做一些试验,结果还是这样吗?
解:不同意他的观点,理由如下:
他再掷一次,正面有可能朝上,反面也有可能朝上,各占,如果小明进行大量的掷质地均匀硬币的试验则正面朝上和正面朝下的的概率会稳定在的附近.
(2)掷一枚质地均匀的硬币,正面朝上的概率为,那么,掷100次硬币,你能保证恰好50次正面朝上吗?为什么?
/答:不能保证.因为概率是针对大量试验而言的,大量试验中所存在的规律并不在一次试验中存在,正面朝上概率是,不能保证2次试验中恰好发生1次,也不能保证在100次试验中恰好发生50次,只是当试验的次数越来越大时,正面朝上的概率会稳定到.
【例题2】(★)在一个不透明的口袋里装有只有颜色不同的黑、白两种颜色的球共30只,某小组做摸球实验,将球搅匀后从中随机摸出一个球记下颜色,再把它放回袋中,不断重复.下表是活动进行中的一组统计数据:
(1)请估计:当n很大时,摸到白球的频率将会接近%// //%;
(2)假如你去摸一次,你摸到白球的概率是%// //%,摸到黑球的概率是%// //%;
(3)试估算口袋中黑、白两种颜色的球各有多少只?
摸球的次数n 100 150 200 500 800 1000 …
摸到白球的次数m 58 96 116 295 484 601 …
摸到白球的频率 0.58 0.64 0.58 0.59 0.605 0.601 …
0.6
0.6
0.4
解:(3)因为摸到白球的概率是0.6,摸到黑球的概率是0.4,所以口袋中黑、白两种颜色的球:白球是30×0.6=18个,黑球是30×0.4=12个.
1.在一个布袋中装有红、白两种颜色的小球,它们除颜色外没有任何其他区别.其中红球若干,白球5个,袋中的球已搅匀.若从袋中随机取出1个球,取出红球的可能性大,则红球的个数是(%////%)
A.4个 B.5 C.不足4个 D.6个或6个以上
D
2.下列事件发生的可能性为0的是(%////%)
A.掷两枚骰子,同时出现数字“6”朝上
B.小明从家里到学校用了10分钟,从学校回到家里却用了15分钟
C.今天是星期天,昨天必定是星期六
D.小明步行的速度是每小时50千米
D
3.关于频率和概率的关系,下列说法正确的是(%////%)
A.频率等于概率
B.当实验次数很大时,频率稳定在概率附近
C.当实验次数很大时,概率稳定在频率附近
D.实验得到的频率与概率不可能相等
B
4.小明做了5次掷质地均匀硬币的试验,其中有2次正面朝上、3次正面朝下.他认为再掷一次,一定正面朝上.你同意他的观点吗?与同伴进行交流.
解:不同意他的观点,理由如下:
他再掷一次,正面有可能朝上,反面也有可能朝上,各占,如果小明进行大量的掷质地均匀硬币的试验则正面朝上的概率为.
5.某位篮球运动员在同样的条件下进行投篮练习,结果如下表:
(1)将上表补充完整;
(2)这位运动员投篮一次,进球的概率约是多少?
(3)若这位运动员投篮10次,必定会投进8次吗?为什么?
投篮次数(n) 8 10 15 20 30 40 50
进球次数(m) 6 8 12 17 25 32 38
进球频率()
解:(1)答案为:0.75;0.8;0.8;0.85;0.83;0.8;0.76;
(2)这位运动员投篮一次,进球的概率约是0.8;
(3)若这位运动员投篮10次,不一定会投进8次.
因为进球的概率是0.8是通过大量重复实验得到的,而投篮10次是随机的,所以不一定会投进8次,可能都不进,也可能都进.
6.(★)掷一枚质地均匀的骰子.
(1)会出现哪些可能的结果?
(2)掷出的点数为1与掷出的点数为2的可能性相同吗?掷出的点数为1与掷出的点数为3的可能性相同吗?
(3)每种结果出现的可能性相同吗?你是怎样做的?
解:(1)会出现1,2,3,4,5,6,一共六种可能的结果;
(2)掷出的点数为1与掷出的点数为2的可能性相同;掷出的点数为1与掷出的点数为3的可能性相同;
(3)1÷6.故每种结果出现的可能性相同.
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
