【五环分层导学-课件】5-4 简单的轴对称图形(2)-北师大版数学七(下)
文档属性
| 名称 | 【五环分层导学-课件】5-4 简单的轴对称图形(2)-北师大版数学七(下) |

|
|
| 格式 | pptx | ||
| 文件大小 | 9.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-30 00:00:00 | ||
图片预览





文档简介
(共12张PPT)
第五章 生活中的轴对称
第4课 简单的轴对称图形(1)
北师大版七年级下册
本套资料以教育部颁布的《数学课程标准(2022)版》为依据,结合新中考改革研究,立足北师大版本教材开发,通过课堂流程的优化设计,内容的层次设计,循序渐进,让不同层次的学生都学有所问,问有所探,探有所获,能力都有不同层次的提高,思维不断生长。
新授课通过激活思维、探究新知、双基巩固、综合运用、分层反馈五个环节来完成。
资料简介
第一环节 激活思维 通过回顾与本节新知有关的旧知或熟悉的生活情境,唤醒、激活学生的旧知,为新知生成奠定基础,为知识的形成提供情境。
第二环节 探究新知 通过一系列问题,引领学生通过自主、合作、探究的方式,在解决问题串的过程中,生成新知,积累基本活动经验,提高分析问题和解决问题的能力。
第三环节 双基巩固 通过典型例题,及时巩固基础知识与基本技能,为学生初步应用新知解决问题积累经验。
第四环节 综合运用 以本节知识为核心,设计一道综合题,提高学生综合运用知识的能力,发散思维,渗透数学思想方法。
第五环节 分层反馈 通过由易到难的当堂练习或检测,及时反馈学生掌握情况,给教师课后针对辅导与布置课后作业的量和难度提供数据参考。
五环导学
(1)如果一个图形沿一条直线折叠后,直线两旁的部分能够互相重合,那么这个图形叫做%// //%,这条直线叫做%// //%.
(2)轴对称的性质:对应点连线段被对称轴%// //%;对应线段%// //%,对应角%// //%.
(3)等腰三角形是%// //%图形;等腰三角形的两个底角%// //%.等腰三角形顶角的平分线,底边上的中线,底边上的高%// //%,它们所在直线都是等腰三角形的%// //%.
轴对称图形
对称轴
垂直平分
相等
相等
轴对称
相等
重合
对称轴
【探究1】已知:如图,在△ABC中,∠B=∠C .求证:AB=AC .
解:如图,过点A作AD⊥BC于点D .
则∠ADB=∠ADC.
∵在△ABD与△ACD中,,
∴△ABD≌△ACD(AAS),
∴AB=AC .
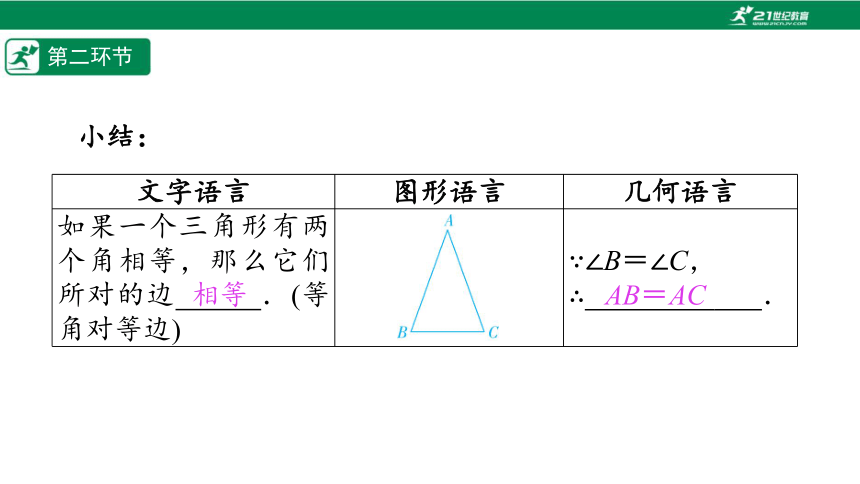
小结:
文字语言 图形语言 几何语言
如果一个三角形有两个角相等,那么它们所对的边%////%.(等角对等边) ∵∠B=∠C,
∴%// //% .
AB=AC
相等
【探究2】如图,等边三角形有几条对称轴,你能发现它的哪些特征?
小结:等边三角形是%// //% 图形,有%////%条对称轴;等边三角形的三边都%// //%,三个角都%// //%,都为%////%度.等边三角形有%////%条三线合一的线.
轴对称
3
相等
相等
60
3
【例题1】如图,AD是等边△ABC的中线,在AC边上截取AE=AD,求∠EDC的度数.
解:∵AD是等边△ABC的中线,
∴AD⊥BC,∠BAD=∠CAD∠BAC60°=30°,
∴∠ADC=90°,
∵AD=AE,
∴∠ADE=∠AED75°,
∴∠EDC=∠ADC-∠ADE=90°-75°=15°.
【例题2】如图,△APB与△CDP是两个全等的等边三角形,且PA⊥PD,有下列四个结论:①∠PBC=15°;②AD∥BC;③直线PC与AB垂直.其中正确的有%// //%.
①②③
1.如图,直线l∥m,等边三角形ABC的顶点B在直线m上,∠1=25°,则∠2的度数为(%////%)
A.35° B.25°
C.30° D.45°
A
2.如图,△EFG的三条边相等,三个内角也相等,且EH=FI=GJ.
△EHJ、△FIH、△GJI全等吗?△HIJ的三边相等吗?
解:由题意可知:EF=FG=EG,∠E=∠F=∠G,
∵EH=FI=GJ,∴EJ=FH=GI,在△EHJ与△FIH中,
,∴△EHJ≌△FIH(SAS),∴HJ=IH,
在△FIH与△GJI中,,
∴△FIH≌△GJI(SAS),∴HI=JI,
∴△EHJ、△FIH、△GJI全等,∴HJ=HI=IJ.
3.(★)如图,△ACD和△BCE都是等腰直角三角形,∠ACD=∠BCE=90°,AE交CD于点F,BD分别交CE、AE于点G、H.试猜测线段AE和BD的数量和位置关系,并说明理由.
解:猜测AE=BD,AE⊥BD;理由如下:∵∠ACD=∠BCE=90°,
∴∠ACD+∠DCE=∠BCE+∠DCE,即∠ACE=∠DCB,
又∵△ACD和△BCE都是等腰直角三角形,∴AC=CD,CE=CB,
在△ACE与△DCB中,,
∴△ACE≌△DCB(SAS),∴AE=BD,∠CAE=∠CDB;
∵∠AFC=∠DFH,∠FAC+∠AFC=90°,
∴∠DHF=∠ACD=90°,
∴AE⊥BD .故线段AE和BD的数量相等,位置是垂直关系.
第五章 生活中的轴对称
第4课 简单的轴对称图形(1)
北师大版七年级下册
本套资料以教育部颁布的《数学课程标准(2022)版》为依据,结合新中考改革研究,立足北师大版本教材开发,通过课堂流程的优化设计,内容的层次设计,循序渐进,让不同层次的学生都学有所问,问有所探,探有所获,能力都有不同层次的提高,思维不断生长。
新授课通过激活思维、探究新知、双基巩固、综合运用、分层反馈五个环节来完成。
资料简介
第一环节 激活思维 通过回顾与本节新知有关的旧知或熟悉的生活情境,唤醒、激活学生的旧知,为新知生成奠定基础,为知识的形成提供情境。
第二环节 探究新知 通过一系列问题,引领学生通过自主、合作、探究的方式,在解决问题串的过程中,生成新知,积累基本活动经验,提高分析问题和解决问题的能力。
第三环节 双基巩固 通过典型例题,及时巩固基础知识与基本技能,为学生初步应用新知解决问题积累经验。
第四环节 综合运用 以本节知识为核心,设计一道综合题,提高学生综合运用知识的能力,发散思维,渗透数学思想方法。
第五环节 分层反馈 通过由易到难的当堂练习或检测,及时反馈学生掌握情况,给教师课后针对辅导与布置课后作业的量和难度提供数据参考。
五环导学
(1)如果一个图形沿一条直线折叠后,直线两旁的部分能够互相重合,那么这个图形叫做%// //%,这条直线叫做%// //%.
(2)轴对称的性质:对应点连线段被对称轴%// //%;对应线段%// //%,对应角%// //%.
(3)等腰三角形是%// //%图形;等腰三角形的两个底角%// //%.等腰三角形顶角的平分线,底边上的中线,底边上的高%// //%,它们所在直线都是等腰三角形的%// //%.
轴对称图形
对称轴
垂直平分
相等
相等
轴对称
相等
重合
对称轴
【探究1】已知:如图,在△ABC中,∠B=∠C .求证:AB=AC .
解:如图,过点A作AD⊥BC于点D .
则∠ADB=∠ADC.
∵在△ABD与△ACD中,,
∴△ABD≌△ACD(AAS),
∴AB=AC .
小结:
文字语言 图形语言 几何语言
如果一个三角形有两个角相等,那么它们所对的边%////%.(等角对等边) ∵∠B=∠C,
∴%// //% .
AB=AC
相等
【探究2】如图,等边三角形有几条对称轴,你能发现它的哪些特征?
小结:等边三角形是%// //% 图形,有%////%条对称轴;等边三角形的三边都%// //%,三个角都%// //%,都为%////%度.等边三角形有%////%条三线合一的线.
轴对称
3
相等
相等
60
3
【例题1】如图,AD是等边△ABC的中线,在AC边上截取AE=AD,求∠EDC的度数.
解:∵AD是等边△ABC的中线,
∴AD⊥BC,∠BAD=∠CAD∠BAC60°=30°,
∴∠ADC=90°,
∵AD=AE,
∴∠ADE=∠AED75°,
∴∠EDC=∠ADC-∠ADE=90°-75°=15°.
【例题2】如图,△APB与△CDP是两个全等的等边三角形,且PA⊥PD,有下列四个结论:①∠PBC=15°;②AD∥BC;③直线PC与AB垂直.其中正确的有%// //%.
①②③
1.如图,直线l∥m,等边三角形ABC的顶点B在直线m上,∠1=25°,则∠2的度数为(%////%)
A.35° B.25°
C.30° D.45°
A
2.如图,△EFG的三条边相等,三个内角也相等,且EH=FI=GJ.
△EHJ、△FIH、△GJI全等吗?△HIJ的三边相等吗?
解:由题意可知:EF=FG=EG,∠E=∠F=∠G,
∵EH=FI=GJ,∴EJ=FH=GI,在△EHJ与△FIH中,
,∴△EHJ≌△FIH(SAS),∴HJ=IH,
在△FIH与△GJI中,,
∴△FIH≌△GJI(SAS),∴HI=JI,
∴△EHJ、△FIH、△GJI全等,∴HJ=HI=IJ.
3.(★)如图,△ACD和△BCE都是等腰直角三角形,∠ACD=∠BCE=90°,AE交CD于点F,BD分别交CE、AE于点G、H.试猜测线段AE和BD的数量和位置关系,并说明理由.
解:猜测AE=BD,AE⊥BD;理由如下:∵∠ACD=∠BCE=90°,
∴∠ACD+∠DCE=∠BCE+∠DCE,即∠ACE=∠DCB,
又∵△ACD和△BCE都是等腰直角三角形,∴AC=CD,CE=CB,
在△ACE与△DCB中,,
∴△ACE≌△DCB(SAS),∴AE=BD,∠CAE=∠CDB;
∵∠AFC=∠DFH,∠FAC+∠AFC=90°,
∴∠DHF=∠ACD=90°,
∴AE⊥BD .故线段AE和BD的数量相等,位置是垂直关系.
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
