【五环分层导学-课件】6-6 单元复习 概率初步-北师大版数学七(下)
文档属性
| 名称 | 【五环分层导学-课件】6-6 单元复习 概率初步-北师大版数学七(下) |

|
|
| 格式 | pptx | ||
| 文件大小 | 10.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-30 00:00:00 | ||
图片预览








文档简介
(共28张PPT)
第六章 概率初步
第6课 单元复习
北师大版七年级下册
本套资料以教育部颁布的《数学课程标准(2022)版》为依据,结合新中考改革研究,立足北师大版本教材开发,通过课堂流程的优化设计,内容的层次设计,循序渐进,让不同层次的学生都学有所问,问有所探,探有所获,能力都有不同层次的提高,思维不断生长。
新授课通过激活思维、探究新知、双基巩固、综合运用、分层反馈五个环节来完成。
资料简介
第一环节 激活思维 通过回顾与本节新知有关的旧知或熟悉的生活情境,唤醒、激活学生的旧知,为新知生成奠定基础,为知识的形成提供情境。
第二环节 探究新知 通过一系列问题,引领学生通过自主、合作、探究的方式,在解决问题串的过程中,生成新知,积累基本活动经验,提高分析问题和解决问题的能力。
第三环节 双基巩固 通过典型例题,及时巩固基础知识与基本技能,为学生初步应用新知解决问题积累经验。
第四环节 综合运用 以本节知识为核心,设计一道综合题,提高学生综合运用知识的能力,发散思维,渗透数学思想方法。
第五环节 分层反馈 通过由易到难的当堂练习或检测,及时反馈学生掌握情况,给教师课后针对辅导与布置课后作业的量和难度提供数据参考。
五环导学
【问题1】举例说明什么是随机事件?
【问题2】事件发生的概率与频率有什么区别和联系?
【问题3】游戏对双方公平是什么意思?你能设计一些对双方都公平的游戏吗?
【问题4】举例说明如何求随机事件的概率.在什么条件下适合用公式P(A)=来求随机事件的概率?
【问题5】梳理本章内容,用你喜欢的方式(思维导图、列表等)呈现全章知识结构.完成后请和同学交流,并加以完善.
【例题1】下列事件中,哪些是随机事件?哪些是必然事件?哪些是不可能事件?
(1)袋中有5个红球,能摸到红球;
(2)袋中有4个红球,1个白球,能摸到红球;
(3)袋中有2个红球,3个白球,能摸到红球;
(4)袋中有5个白球,能摸到红球.
解:随机事件:(2)(3);
必然事件:(1);
不可能事件:(4).
【例题2】下列事件属于确定事件的是(%////%)
A.未来一个月重庆市新冠肺炎新增零人
B.明天太阳从东边升起
C.单项式加上单项式,和为多项式
D.掷一枚质地均匀的硬币正面朝上
B
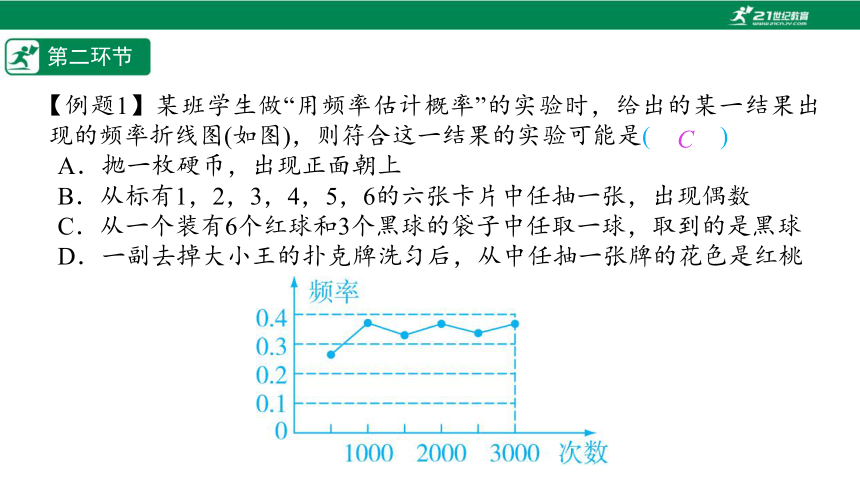
【例题1】某班学生做“用频率估计概率”的实验时,给出的某一结果出现的频率折线图(如图),则符合这一结果的实验可能是(%////%)
A.抛一枚硬币,出现正面朝上
B.从标有1,2,3,4,5,6的六张卡片中任抽一张,出现偶数
C.从一个装有6个红球和3个黑球的袋子中任取一球,取到的是黑球
D.一副去掉大小王的扑克牌洗匀后,从中任抽一张牌的花色是红桃
C
【例题2】在一个不透明的袋中,装有1个白球、2个红球、2个黄球、3个黑球,它们除颜色外都相同,从袋中任意摸出一个球,可能性最大的是(%////%)
A.白球 B.红球 C.黄球 D.黑球
【例题3】若气象部门预报明天下雨的概率是65%,下列说法正确的是(%////%)
A.明天一定会下雨 B.明天一定不会下雨
C.明天下雨的可能性较大 D.明天下雨的可能性较小
D
C
【例题1】现有8张同样的卡片,分别标有数字:1,1,2,2,2,3,4,5,将这些卡片放在一个不透明的盒子里,搅匀后从中随机地抽出一张,抽到标有数字2的
卡片的概率是%////%.
【例题2】已知袋中有若干个球,其中只有2个红球,它们除颜色外其它都相同.若随机从中摸出一个,摸到红球的概率是,则袋中球的总个数是%////%个.
8
【例题1】如图,正方形ABCD内的图形来自中国古代的太极图,现随机向正方形内掷一枚小针,则针尖落在黑色区域内的概率为(%////%)
A. B.
C. D.
C
【例题2】如图是一个可以自由转动的转盘,转盘分成黑、白两种颜色,指针的位置固定,转动的转盘停止后,指针恰好指向白色扇形的穊率为(指针指向OA时,当作指向黑色扇形;指针指OB时,当作指向白色扇形),则黑色扇形的圆心角∠AOB=%// //%.
45°
【例题1】为丰富学生的文体生活,深圳 (学校)准备成立“声乐、演讲、舞蹈、足球、篮球”五个社团,要求每个学生都参加一个社团且每人只能参加一个社团.为了了解即将参加每个社团的大致人数,学校对部分学生进行了抽样调查在整理调查数据的过程中,绘制出如图所示的两幅不完整的统计图,请你根据图中信息解答下列问题:
(1)被抽查的学生一共有多少人?
(2)将条形统计图补充完整.
(3)若全校有学生1500人,请你
估计全校有意参加“声乐”社团
的学生人数.
(4)从被抽查的学生中随意选出
1人,该学生恰好选择参加“演
讲”社团的概率是多少?
解:(1)被抽查的学生数是:15÷15%=100(人);
(2)舞蹈人数有100×20%=20(人),补图如右:
(3)根据题意得:1500×=330(人),
答:估计全校有意参加“声乐”社团的学生人数有330人;
(4)该学生恰好选择参加“演讲”社团的概率是:=.
对点练习:下列说法正确的是(%////%)
A.某市“明天降雨的概率是75%”表示明天有75%的时间会降雨
B.400人中一定有两人的生日在同一天
C.在抽奖活动中,“中奖的概率是”表示抽奖100次就一定会中奖
D.十五的月亮像一个弯弯的细钩
对点练习:某地气象局预报称:“明天本市降水概率为30%”,这句话指的是(%////%)
A.明天该市30%的时间下雨 B.明天该市30%的地区下雨
C.明天该市一定不下雨 D.明天该市下雨的可能性是30%
B
D
对点练习:一个不透明的布袋中放有大小、质地都相同四个红球和五个白球,小敏第一次从布袋中摸出一个红球后不放回布袋中,接看第二次从布袋中摸球,那么小敏第二次还是摸出红球的可能性为%////%.
1.下列事件中,属于必然事件的是(%////%)
A.一个数的相反数等于它本身
B.早上的太阳从北方升起
C.380人中有两人的生日在同一天
D.明天上学路上遇到下雨
C
2.下列说法正确的是(%////%)
A.如果一件事发生的机会只有千万分之一,那么它就是不可能事件
B.如果一件事发生的机会达99.999%,那么它就是必然事件
C.如果一件事不是不可能事件,那么它就是必然事件
D.如果一件事不是必然事件,那么它就是不可能事件或随机事件
D
3.在不透明的袋子里装有颜色不同的16个红球和若干个白球,每次从袋子里摸出来一个球记录下颜色后再放回,经过多次重复试验,发现摸到白球的频率稳定在0.6,估计袋中白球有(%////%)
A.40个 B.38个 C.26个 D.24个
D
4.数学老师将全班分成7个小组开展小组合作学习,采用随机抽签法确定一个小组进行展示活动.则第3小组被抽到的概率是(%////%)
A. B. C. D.
A
5.如图,转动质量均匀的转盘,当转盘停止时,指针落在白色区域的概率是(%////%)
A. B.
C. D.
A
6.如图,一个游戏转盘中,红、黄、蓝三个扇形的圆心角度数分别为60°,90°,210°.让转盘自由转动,指针停止后落在黄色区域的概率是(%////%)
A. B.
C. D.
B
7.如图,在方格纸中,随机选择标有序号①②③④⑤⑥中的一个小正方形涂黑,与图中的阴影部分构成轴对称图形的概率是(%////%)
A. B.
C. D.
A
8.为庆祝新中国成立70周年,某校开展以“我和我亲爱的祖国”为主题的“快闪”活动,七年级准备从两名男生和三名女生中选出一名同学领唱,如果每一位同学被选中的机会均等,则选出的恰为女生的概率是%////%.
9.一个不透明的袋子中有2个黑球和1个白球,每个球除颜色外都相同,任意摸出两个球,则恰好是一黑一白的概率是%////%.
10.从-3.-1,π,0,3这五个数中随机抽取一个数,恰好是负数的概率是%////%.
11.一个正方体骰子,其中一个面上标有“1”,两个面上标有“2”,三个面上标有“3”,求将这个骰子掷出后:
(1)“2”朝上的概率;
(2)朝上概率最大的数;
(3)如果规定朝上的数为1或2时,甲胜;朝上的数为3时乙胜,则甲、乙谁获胜的机会大些?
/解:(1)“2”朝上的概率为;
(2)“1”朝上的概率为,
“2”朝上概率为,
“3”朝上概率为.
∴朝上概率最大的数为3.
(3)甲胜的概率为,乙胜的概率为,
他们获胜的概率相等,所以获胜机会相等.
12.如图,是一个圆形转盘,现按1∶2∶3∶4分成四个部分,分别涂上红、黄、蓝、绿四种颜色,自由转动转盘,请计算:
(1)停止后指针落在蓝色区域的概率;
(2)黄色区域扇形的圆心角度数是多少?
解:(1)∵圆被等分成1+2+3+4=10份,其中蓝色部分占3份,
∴停止后指针落在蓝色区域的概率为:;
(2)360°=72°,
答:黄色区域扇形的圆心角度数是72°.
第六章 概率初步
第6课 单元复习
北师大版七年级下册
本套资料以教育部颁布的《数学课程标准(2022)版》为依据,结合新中考改革研究,立足北师大版本教材开发,通过课堂流程的优化设计,内容的层次设计,循序渐进,让不同层次的学生都学有所问,问有所探,探有所获,能力都有不同层次的提高,思维不断生长。
新授课通过激活思维、探究新知、双基巩固、综合运用、分层反馈五个环节来完成。
资料简介
第一环节 激活思维 通过回顾与本节新知有关的旧知或熟悉的生活情境,唤醒、激活学生的旧知,为新知生成奠定基础,为知识的形成提供情境。
第二环节 探究新知 通过一系列问题,引领学生通过自主、合作、探究的方式,在解决问题串的过程中,生成新知,积累基本活动经验,提高分析问题和解决问题的能力。
第三环节 双基巩固 通过典型例题,及时巩固基础知识与基本技能,为学生初步应用新知解决问题积累经验。
第四环节 综合运用 以本节知识为核心,设计一道综合题,提高学生综合运用知识的能力,发散思维,渗透数学思想方法。
第五环节 分层反馈 通过由易到难的当堂练习或检测,及时反馈学生掌握情况,给教师课后针对辅导与布置课后作业的量和难度提供数据参考。
五环导学
【问题1】举例说明什么是随机事件?
【问题2】事件发生的概率与频率有什么区别和联系?
【问题3】游戏对双方公平是什么意思?你能设计一些对双方都公平的游戏吗?
【问题4】举例说明如何求随机事件的概率.在什么条件下适合用公式P(A)=来求随机事件的概率?
【问题5】梳理本章内容,用你喜欢的方式(思维导图、列表等)呈现全章知识结构.完成后请和同学交流,并加以完善.
【例题1】下列事件中,哪些是随机事件?哪些是必然事件?哪些是不可能事件?
(1)袋中有5个红球,能摸到红球;
(2)袋中有4个红球,1个白球,能摸到红球;
(3)袋中有2个红球,3个白球,能摸到红球;
(4)袋中有5个白球,能摸到红球.
解:随机事件:(2)(3);
必然事件:(1);
不可能事件:(4).
【例题2】下列事件属于确定事件的是(%////%)
A.未来一个月重庆市新冠肺炎新增零人
B.明天太阳从东边升起
C.单项式加上单项式,和为多项式
D.掷一枚质地均匀的硬币正面朝上
B
【例题1】某班学生做“用频率估计概率”的实验时,给出的某一结果出现的频率折线图(如图),则符合这一结果的实验可能是(%////%)
A.抛一枚硬币,出现正面朝上
B.从标有1,2,3,4,5,6的六张卡片中任抽一张,出现偶数
C.从一个装有6个红球和3个黑球的袋子中任取一球,取到的是黑球
D.一副去掉大小王的扑克牌洗匀后,从中任抽一张牌的花色是红桃
C
【例题2】在一个不透明的袋中,装有1个白球、2个红球、2个黄球、3个黑球,它们除颜色外都相同,从袋中任意摸出一个球,可能性最大的是(%////%)
A.白球 B.红球 C.黄球 D.黑球
【例题3】若气象部门预报明天下雨的概率是65%,下列说法正确的是(%////%)
A.明天一定会下雨 B.明天一定不会下雨
C.明天下雨的可能性较大 D.明天下雨的可能性较小
D
C
【例题1】现有8张同样的卡片,分别标有数字:1,1,2,2,2,3,4,5,将这些卡片放在一个不透明的盒子里,搅匀后从中随机地抽出一张,抽到标有数字2的
卡片的概率是%////%.
【例题2】已知袋中有若干个球,其中只有2个红球,它们除颜色外其它都相同.若随机从中摸出一个,摸到红球的概率是,则袋中球的总个数是%////%个.
8
【例题1】如图,正方形ABCD内的图形来自中国古代的太极图,现随机向正方形内掷一枚小针,则针尖落在黑色区域内的概率为(%////%)
A. B.
C. D.
C
【例题2】如图是一个可以自由转动的转盘,转盘分成黑、白两种颜色,指针的位置固定,转动的转盘停止后,指针恰好指向白色扇形的穊率为(指针指向OA时,当作指向黑色扇形;指针指OB时,当作指向白色扇形),则黑色扇形的圆心角∠AOB=%// //%.
45°
【例题1】为丰富学生的文体生活,深圳 (学校)准备成立“声乐、演讲、舞蹈、足球、篮球”五个社团,要求每个学生都参加一个社团且每人只能参加一个社团.为了了解即将参加每个社团的大致人数,学校对部分学生进行了抽样调查在整理调查数据的过程中,绘制出如图所示的两幅不完整的统计图,请你根据图中信息解答下列问题:
(1)被抽查的学生一共有多少人?
(2)将条形统计图补充完整.
(3)若全校有学生1500人,请你
估计全校有意参加“声乐”社团
的学生人数.
(4)从被抽查的学生中随意选出
1人,该学生恰好选择参加“演
讲”社团的概率是多少?
解:(1)被抽查的学生数是:15÷15%=100(人);
(2)舞蹈人数有100×20%=20(人),补图如右:
(3)根据题意得:1500×=330(人),
答:估计全校有意参加“声乐”社团的学生人数有330人;
(4)该学生恰好选择参加“演讲”社团的概率是:=.
对点练习:下列说法正确的是(%////%)
A.某市“明天降雨的概率是75%”表示明天有75%的时间会降雨
B.400人中一定有两人的生日在同一天
C.在抽奖活动中,“中奖的概率是”表示抽奖100次就一定会中奖
D.十五的月亮像一个弯弯的细钩
对点练习:某地气象局预报称:“明天本市降水概率为30%”,这句话指的是(%////%)
A.明天该市30%的时间下雨 B.明天该市30%的地区下雨
C.明天该市一定不下雨 D.明天该市下雨的可能性是30%
B
D
对点练习:一个不透明的布袋中放有大小、质地都相同四个红球和五个白球,小敏第一次从布袋中摸出一个红球后不放回布袋中,接看第二次从布袋中摸球,那么小敏第二次还是摸出红球的可能性为%////%.
1.下列事件中,属于必然事件的是(%////%)
A.一个数的相反数等于它本身
B.早上的太阳从北方升起
C.380人中有两人的生日在同一天
D.明天上学路上遇到下雨
C
2.下列说法正确的是(%////%)
A.如果一件事发生的机会只有千万分之一,那么它就是不可能事件
B.如果一件事发生的机会达99.999%,那么它就是必然事件
C.如果一件事不是不可能事件,那么它就是必然事件
D.如果一件事不是必然事件,那么它就是不可能事件或随机事件
D
3.在不透明的袋子里装有颜色不同的16个红球和若干个白球,每次从袋子里摸出来一个球记录下颜色后再放回,经过多次重复试验,发现摸到白球的频率稳定在0.6,估计袋中白球有(%////%)
A.40个 B.38个 C.26个 D.24个
D
4.数学老师将全班分成7个小组开展小组合作学习,采用随机抽签法确定一个小组进行展示活动.则第3小组被抽到的概率是(%////%)
A. B. C. D.
A
5.如图,转动质量均匀的转盘,当转盘停止时,指针落在白色区域的概率是(%////%)
A. B.
C. D.
A
6.如图,一个游戏转盘中,红、黄、蓝三个扇形的圆心角度数分别为60°,90°,210°.让转盘自由转动,指针停止后落在黄色区域的概率是(%////%)
A. B.
C. D.
B
7.如图,在方格纸中,随机选择标有序号①②③④⑤⑥中的一个小正方形涂黑,与图中的阴影部分构成轴对称图形的概率是(%////%)
A. B.
C. D.
A
8.为庆祝新中国成立70周年,某校开展以“我和我亲爱的祖国”为主题的“快闪”活动,七年级准备从两名男生和三名女生中选出一名同学领唱,如果每一位同学被选中的机会均等,则选出的恰为女生的概率是%////%.
9.一个不透明的袋子中有2个黑球和1个白球,每个球除颜色外都相同,任意摸出两个球,则恰好是一黑一白的概率是%////%.
10.从-3.-1,π,0,3这五个数中随机抽取一个数,恰好是负数的概率是%////%.
11.一个正方体骰子,其中一个面上标有“1”,两个面上标有“2”,三个面上标有“3”,求将这个骰子掷出后:
(1)“2”朝上的概率;
(2)朝上概率最大的数;
(3)如果规定朝上的数为1或2时,甲胜;朝上的数为3时乙胜,则甲、乙谁获胜的机会大些?
/解:(1)“2”朝上的概率为;
(2)“1”朝上的概率为,
“2”朝上概率为,
“3”朝上概率为.
∴朝上概率最大的数为3.
(3)甲胜的概率为,乙胜的概率为,
他们获胜的概率相等,所以获胜机会相等.
12.如图,是一个圆形转盘,现按1∶2∶3∶4分成四个部分,分别涂上红、黄、蓝、绿四种颜色,自由转动转盘,请计算:
(1)停止后指针落在蓝色区域的概率;
(2)黄色区域扇形的圆心角度数是多少?
解:(1)∵圆被等分成1+2+3+4=10份,其中蓝色部分占3份,
∴停止后指针落在蓝色区域的概率为:;
(2)360°=72°,
答:黄色区域扇形的圆心角度数是72°.
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
