【五环分层导学-课件】3-4 用图象表示的变量间关系(2)-北师大版数学七(下)
文档属性
| 名称 | 【五环分层导学-课件】3-4 用图象表示的变量间关系(2)-北师大版数学七(下) |

|
|
| 格式 | pptx | ||
| 文件大小 | 10.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-30 00:00:00 | ||
图片预览





文档简介
(共14张PPT)
第三章 变量之间的关系
第4课 用图象表示的变量间关系(2)
北师大版七年级下册
本套资料以教育部颁布的《数学课程标准(2022)版》为依据,结合新中考改革研究,立足北师大版本教材开发,通过课堂流程的优化设计,内容的层次设计,循序渐进,让不同层次的学生都学有所问,问有所探,探有所获,能力都有不同层次的提高,思维不断生长。
新授课通过激活思维、探究新知、双基巩固、综合运用、分层反馈五个环节来完成。
资料简介
第一环节 激活思维 通过回顾与本节新知有关的旧知或熟悉的生活情境,唤醒、激活学生的旧知,为新知生成奠定基础,为知识的形成提供情境。
第二环节 探究新知 通过一系列问题,引领学生通过自主、合作、探究的方式,在解决问题串的过程中,生成新知,积累基本活动经验,提高分析问题和解决问题的能力。
第三环节 双基巩固 通过典型例题,及时巩固基础知识与基本技能,为学生初步应用新知解决问题积累经验。
第四环节 综合运用 以本节知识为核心,设计一道综合题,提高学生综合运用知识的能力,发散思维,渗透数学思想方法。
第五环节 分层反馈 通过由易到难的当堂练习或检测,及时反馈学生掌握情况,给教师课后针对辅导与布置课后作业的量和难度提供数据参考。
五环导学
变量的表示方法 优势
表格法
关系式法
图象法
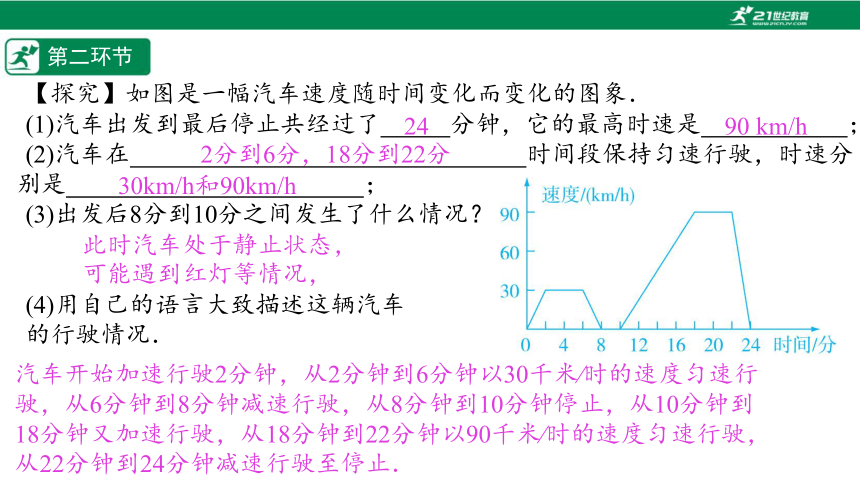
【探究】如图是一幅汽车速度随时间变化而变化的图象.
(1)汽车出发到最后停止共经过了%////%分钟,它的最高时速是%// //%;
(2)汽车在%// //%时间段保持匀速行驶,时速分别是%// //%;
(3)出发后8分到10分之间发生了什么情况?
(4)用自己的语言大致描述这辆汽车
的行驶情况.
24
90 km/h
2分到6分,18分到22分
30km/h和90km/h
此时汽车处于静止状态,可能遇到红灯等情况,
汽车开始加速行驶2分钟,从2分钟到6分钟以30千米∕时的速度匀速行驶,从6分钟到8分钟减速行驶,从8分钟到10分钟停止,从10分钟到18分钟又加速行驶,从18分钟到22分钟以90千米∕时的速度匀速行驶,从22分钟到24分钟减速行驶至停止.
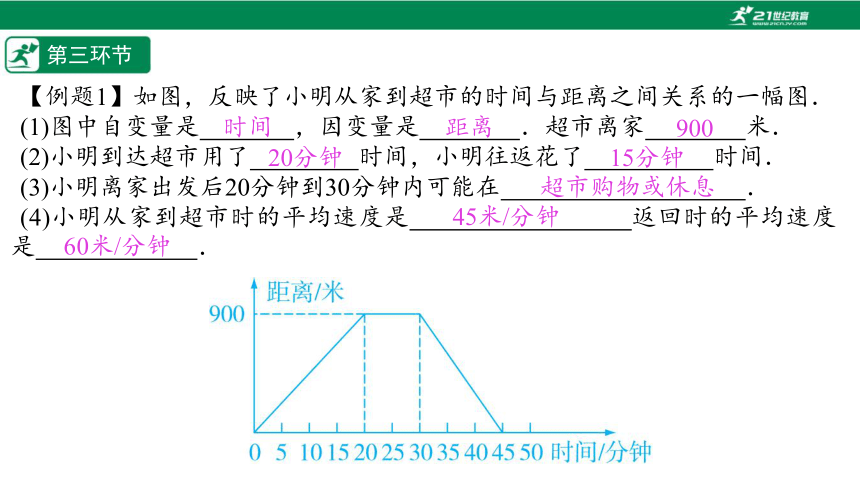
【例题1】如图,反映了小明从家到超市的时间与距离之间关系的一幅图.
(1)图中自变量是%// //%,因变量是%// //%.超市离家%// //%米.
(2)小明到达超市用了%// //%时间,小明往返花了%// //%时间.
(3)小明离家出发后20分钟到30分钟内可能在%// //%.
(4)小明从家到超市时的平均速度是%// //%返回时的平均速度是%// //%.
时间
距离
900
20分钟
15分钟
超市购物或休息
45米/分钟
60米/分钟
【例题2】如图是小明的爸爸骑一辆摩托车从家里出发,离家的距离(千米)随行驶时间(分)的变化而变化的情况:
(1)图象表示了哪两个变量之间的关系?哪个是自变量?哪个是因变量?
(2)小明的爸爸从出发到最后停止共经过了多少分钟?离家最远的距离是多少千米?
(3)摩托车在哪一段时间内速度最快?最快速度是多少千米/小时?
解:(1)图象表示了小明的爸爸离家的距离和行驶时间之间的关系,行驶时间是自变量,小明的爸爸离家的距离是因变量;
(2)由图可得,摩托车从出发到最后停止共经过:100分钟;
离家最远的距离是:40千米.
(3)摩托车在20~50分钟内速度最快;
最快速度是:3060(千米/小时).
1.一辆公共汽车从车站开出,加速行驶一段时间后匀速行驶,过了一段时间,汽车到达下一个车站.乘客上下车后汽车开始加速,一段时间后又开始匀速行驶,下面可以近似地刻画出汽车在这段时间内的速度变化情况的图象是(%////%)
C
2.一艘轮船在同一航线上往返于甲、乙两地.已知轮船在静水中的速度为15 km/h,水流速度为5 km/h.轮船先从甲地顺水航行到乙地,在乙地停留一段时间后,又从乙地逆水航行返回到甲地.设轮船从甲地出发后所用时间为t( h),航行的路程为s(km),则s与t的函数图象大致是(%////%)
C
3.一天,亮亮发烧了,早晨他烧得厉害,吃过药后感觉好多了,中午时亮亮的体温基本正常,但是下午他的体温又开始上升,直到半夜亮亮才感觉身上不那么烫了.下面各图能基本上反映出亮亮这一天(0时~24时)体温的变化情况的是(%////%)
C
4.中国国际大数据产业博览会于2019年5月26日在贵阳开幕,小咏从家出发前往会展中心参观,先匀速步行至轻轨车站,等了一会儿,小咏搭乘轻轨至会展中心参观,参观结束后,小咏搭乘邻居刘叔叔的车顺利到家,下面的哪个图更好地刻画小咏离家距离与时间的关系(%////%)
A
5.(★)如图,表示一骑自行车者与一骑摩托车者沿相同路线由甲地到乙地行驶过程的图象,两地间的距离是100千米,请根据图象回答或解决下面的问题:
(1)谁出发的较早?早多长时间?谁到达乙地早?早到多长时间?
(2)两人在途中行驶的速度分别是多少?
(3)请问在什么时间段内两车均行驶在
途中?什么时间段内自行车行驶在摩
托车前面?什么时间自行车与摩托车
相遇?什么时间段内自行车行驶在摩
托车后面?
解:(1)由图可以看出,自行车出发较早,早3个小时,摩托车到达乙地较早,早3个小时;
(2)对自行车而言,行驶的距离是100千米,耗时8个小时.
所以其速度是:100÷8=12.5(千米/时);
对摩托车而言,行驶的距离是100千米,耗时2个小时.
所以其速度是:100÷2=50(千米/时);
(3)在3<t<5时间段内两车均行驶在途中.
当3<t<4时,自行车在摩托车前面;
当t=4时,两车相遇;
当4<t<5时,自行车在摩托车的后面.
第三章 变量之间的关系
第4课 用图象表示的变量间关系(2)
北师大版七年级下册
本套资料以教育部颁布的《数学课程标准(2022)版》为依据,结合新中考改革研究,立足北师大版本教材开发,通过课堂流程的优化设计,内容的层次设计,循序渐进,让不同层次的学生都学有所问,问有所探,探有所获,能力都有不同层次的提高,思维不断生长。
新授课通过激活思维、探究新知、双基巩固、综合运用、分层反馈五个环节来完成。
资料简介
第一环节 激活思维 通过回顾与本节新知有关的旧知或熟悉的生活情境,唤醒、激活学生的旧知,为新知生成奠定基础,为知识的形成提供情境。
第二环节 探究新知 通过一系列问题,引领学生通过自主、合作、探究的方式,在解决问题串的过程中,生成新知,积累基本活动经验,提高分析问题和解决问题的能力。
第三环节 双基巩固 通过典型例题,及时巩固基础知识与基本技能,为学生初步应用新知解决问题积累经验。
第四环节 综合运用 以本节知识为核心,设计一道综合题,提高学生综合运用知识的能力,发散思维,渗透数学思想方法。
第五环节 分层反馈 通过由易到难的当堂练习或检测,及时反馈学生掌握情况,给教师课后针对辅导与布置课后作业的量和难度提供数据参考。
五环导学
变量的表示方法 优势
表格法
关系式法
图象法
【探究】如图是一幅汽车速度随时间变化而变化的图象.
(1)汽车出发到最后停止共经过了%////%分钟,它的最高时速是%// //%;
(2)汽车在%// //%时间段保持匀速行驶,时速分别是%// //%;
(3)出发后8分到10分之间发生了什么情况?
(4)用自己的语言大致描述这辆汽车
的行驶情况.
24
90 km/h
2分到6分,18分到22分
30km/h和90km/h
此时汽车处于静止状态,可能遇到红灯等情况,
汽车开始加速行驶2分钟,从2分钟到6分钟以30千米∕时的速度匀速行驶,从6分钟到8分钟减速行驶,从8分钟到10分钟停止,从10分钟到18分钟又加速行驶,从18分钟到22分钟以90千米∕时的速度匀速行驶,从22分钟到24分钟减速行驶至停止.
【例题1】如图,反映了小明从家到超市的时间与距离之间关系的一幅图.
(1)图中自变量是%// //%,因变量是%// //%.超市离家%// //%米.
(2)小明到达超市用了%// //%时间,小明往返花了%// //%时间.
(3)小明离家出发后20分钟到30分钟内可能在%// //%.
(4)小明从家到超市时的平均速度是%// //%返回时的平均速度是%// //%.
时间
距离
900
20分钟
15分钟
超市购物或休息
45米/分钟
60米/分钟
【例题2】如图是小明的爸爸骑一辆摩托车从家里出发,离家的距离(千米)随行驶时间(分)的变化而变化的情况:
(1)图象表示了哪两个变量之间的关系?哪个是自变量?哪个是因变量?
(2)小明的爸爸从出发到最后停止共经过了多少分钟?离家最远的距离是多少千米?
(3)摩托车在哪一段时间内速度最快?最快速度是多少千米/小时?
解:(1)图象表示了小明的爸爸离家的距离和行驶时间之间的关系,行驶时间是自变量,小明的爸爸离家的距离是因变量;
(2)由图可得,摩托车从出发到最后停止共经过:100分钟;
离家最远的距离是:40千米.
(3)摩托车在20~50分钟内速度最快;
最快速度是:3060(千米/小时).
1.一辆公共汽车从车站开出,加速行驶一段时间后匀速行驶,过了一段时间,汽车到达下一个车站.乘客上下车后汽车开始加速,一段时间后又开始匀速行驶,下面可以近似地刻画出汽车在这段时间内的速度变化情况的图象是(%////%)
C
2.一艘轮船在同一航线上往返于甲、乙两地.已知轮船在静水中的速度为15 km/h,水流速度为5 km/h.轮船先从甲地顺水航行到乙地,在乙地停留一段时间后,又从乙地逆水航行返回到甲地.设轮船从甲地出发后所用时间为t( h),航行的路程为s(km),则s与t的函数图象大致是(%////%)
C
3.一天,亮亮发烧了,早晨他烧得厉害,吃过药后感觉好多了,中午时亮亮的体温基本正常,但是下午他的体温又开始上升,直到半夜亮亮才感觉身上不那么烫了.下面各图能基本上反映出亮亮这一天(0时~24时)体温的变化情况的是(%////%)
C
4.中国国际大数据产业博览会于2019年5月26日在贵阳开幕,小咏从家出发前往会展中心参观,先匀速步行至轻轨车站,等了一会儿,小咏搭乘轻轨至会展中心参观,参观结束后,小咏搭乘邻居刘叔叔的车顺利到家,下面的哪个图更好地刻画小咏离家距离与时间的关系(%////%)
A
5.(★)如图,表示一骑自行车者与一骑摩托车者沿相同路线由甲地到乙地行驶过程的图象,两地间的距离是100千米,请根据图象回答或解决下面的问题:
(1)谁出发的较早?早多长时间?谁到达乙地早?早到多长时间?
(2)两人在途中行驶的速度分别是多少?
(3)请问在什么时间段内两车均行驶在
途中?什么时间段内自行车行驶在摩
托车前面?什么时间自行车与摩托车
相遇?什么时间段内自行车行驶在摩
托车后面?
解:(1)由图可以看出,自行车出发较早,早3个小时,摩托车到达乙地较早,早3个小时;
(2)对自行车而言,行驶的距离是100千米,耗时8个小时.
所以其速度是:100÷8=12.5(千米/时);
对摩托车而言,行驶的距离是100千米,耗时2个小时.
所以其速度是:100÷2=50(千米/时);
(3)在3<t<5时间段内两车均行驶在途中.
当3<t<4时,自行车在摩托车前面;
当t=4时,两车相遇;
当4<t<5时,自行车在摩托车的后面.
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
