【五环分层导学-课件】2-8 单元复习 相交线与平行线-北师大版数学七(下)
文档属性
| 名称 | 【五环分层导学-课件】2-8 单元复习 相交线与平行线-北师大版数学七(下) |

|
|
| 格式 | pptx | ||
| 文件大小 | 24.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-30 00:00:00 | ||
图片预览









文档简介
(共40张PPT)
第二章 相交线与平行线
第8课 单元复习
北师大版七年级下册
本套资料以教育部颁布的《数学课程标准(2022)版》为依据,结合新中考改革研究,立足北师大版本教材开发,通过课堂流程的优化设计,内容的层次设计,循序渐进,让不同层次的学生都学有所问,问有所探,探有所获,能力都有不同层次的提高,思维不断生长。
资料简介
【问题1】找出生活中的对顶角、互补的角与互余的角.
【问题2】判断两条直线是否平行,通常有哪些途径?
【问题3】平行线有哪些特征?
【问题4】怎样用尺规作一个角等于已知角?
【问题5】梳理本章内容,用你喜欢的方式(思维导图、列表等)呈现全章知识结构.完成后请和同学交流,并加以完善.
同位角相等,两直线平行;内错角相等,两直线平行;同旁内角互补,两直线平行./
平行线没有交点;
两直线平行,同位角相等;
两直线平行,内错角相等;
两直线平行,同旁内角互补.
【例题1】如图,在直线MN的异侧有A、B两点,按要求画图取点,并注明画图取点的依据.
(1)在直线MN上取一点C,使线段AC最短.依据是%// //%.
(2)在直线MN上取一点D,使线段AD+BD最短.依据是%// //%.
垂线段最短
两点之间,线段最短
【例题2】如图,已知直线AB、CD、EF相交于点O,OG⊥CD,∠BOD=24°.
(1)求∠AOG的度数;
(2)若OC是∠AOE的平分线,那么OG是∠AOF的平分线吗?说明你的理由.
解:(1)∵AB、CD相交于点O,
∴∠AOC=∠BOD=24°,
∵OG⊥CD,∴∠COG=90°,
即∠AOC+∠AOG=90°,
∴∠AOG=90°-∠AOC
=90°-24°=66°;
(2)OG是∠AOF的角平分线,理由如下:
∵OC是∠AOE的角平分线,∴∠AOC=∠COE,
又∵∠DOF=∠COE,∴∠COA=∠DOF,
∵OG⊥CD,∴∠COG=∠DOG=90°,
∴∠AOG=∠GOF,∴OG平分∠AOF.
【例题3】如图,直线AB,CD相交于点O,OD平分∠BOE,OF平分∠AOE.
(1)若∠BOE=58°,∠AOE=122°,判断OF与OD的位置关系,并进行证明
(2)若∠AOC∶∠AOD=1∶5,求∠EOF的度数.
(1)OF⊥OD .
证明:∵OD平分∠BOE,OF平分∠AOE,
∠BOE=58°,∠AOE=122°
∴∠FOE∠AOE=61°,∠EOD∠EOB=29°,
∴∠FOD=∠FOE+∠EOD
(∠AOE+∠EOB)=90°,
∴OF⊥OD;
(2)解:∵∠AOC∶∠AOD=1∶5,∠AOC=∠BOD,
∴∠BOD∶∠AOD=1∶5,
∵∠AOD+∠BOD=180°,
∴∠BOD=30°,∠AOD=150°,
∵OD平分∠BOE,OF平分∠AOE,
∴∠BOE=2∠BOD=60°,∠EOF∠AOE.
∵∠AOE+∠BOE=180°,
∴∠AOE=120°,∴∠EOF=60°.
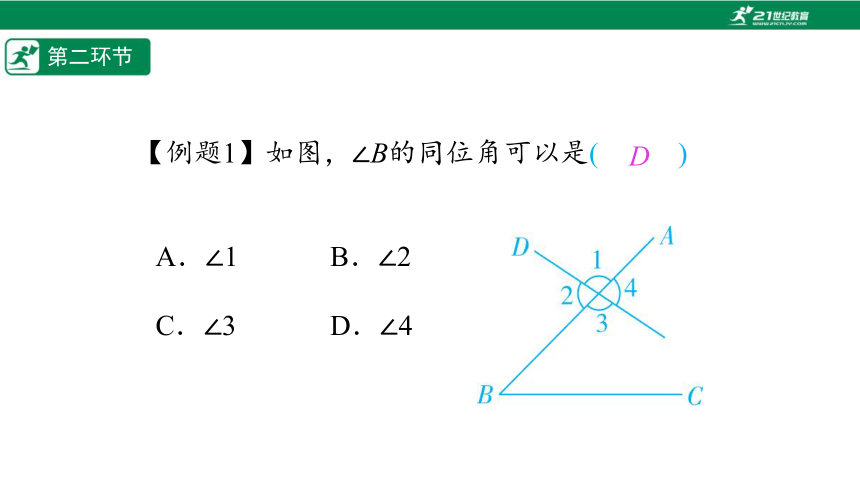
【例题1】如图,∠B的同位角可以是(%////%)
A.∠1 B.∠2
C.∠3 D.∠4
D
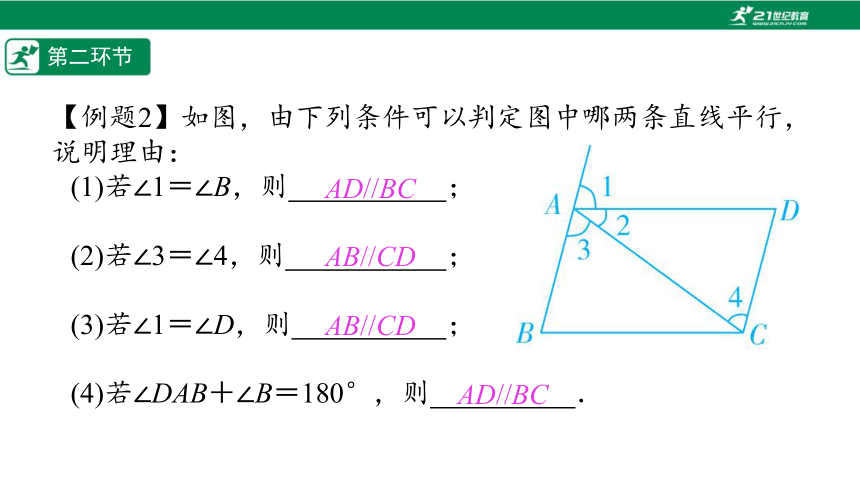
【例题2】如图,由下列条件可以判定图中哪两条直线平行,说明理由:
(1)若∠1=∠B,则%// //%;
(2)若∠3=∠4,则%// //%;
(3)若∠1=∠D,则%// //%;
(4)若∠DAB+∠B=180°,则%// //%.
AD//BC
AB//CD
AB//CD
AD//BC
【例题3】如图,已知∠AEM=∠DGN,求证:AB//CD .
证明:∵∠AEM=∠DGN,∠DGN=∠CGM,
∴∠AEM=∠CGM,
∴AB//CD(同位角相等,两直线平行)/
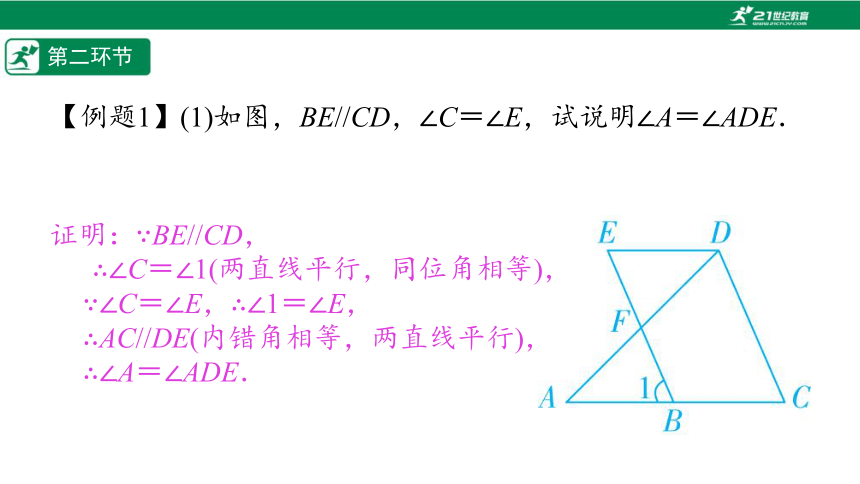
【例题1】(1)如图,BE//CD,∠C=∠E,试说明∠A=∠ADE.
证明:∵BE//CD,
∴∠C=∠1(两直线平行,同位角相等),
∵∠C=∠E,∴∠1=∠E,
∴AC//DE(内错角相等,两直线平行),
∴∠A=∠ADE.
(2)已知:如图,∠1=∠2,∠C=∠D,求证:∠DBC+∠D=180°.
证明:∵∠1=∠2(已知),又∠1=∠DMN(对顶角相等),
∴∠2=∠DMN(等量代换),
∴DB//EC(同位角相等,两直线平行),
∴∠DBC+∠C=180°(两直线平行,同旁内角互补).
∵∠C=∠D(已知),∴∠DBC+∠D=180°(等量代换).
【例题1】尺规作图是指(%////%)
A.用直尺和圆规作图
B.用直尺规范作图
C.用刻度尺和圆规作图
D.用没有刻度的直尺和圆规作图
【例题2】下列各说法一定成立的是(%////%)
A.画直线AB=10厘米
B.已知A、B、C三点,过这三点画一条直线
C.画射线OB=10厘米
D.过直线AB外一点画一条直线和直线AB平行
D
D
【例题1】直线AB∥CD,E为直线AB、CD之间的一点,完成以下问题:
(1)如图-①,若∠B=15°,∠BED=90°,则∠D=%// //%;
(2)如图-②,若∠B=α,∠D=β,求出∠BED的度数(用a、β表示);
(3)如图-③,若∠B=α,∠C=β,则a、β与∠BEC之间有什么等量关系?请猜想证明.
解:(1)过E作EF∥AB,∵AB∥CD,∴EF∥CD,
∵∠B=15°,∴∠BEF=15°,
又∵∠BED=90°,∴∠DEF=75°,
∵EF∥CD,∴∠D=75°,故答案为:75°;
(2)过E作EF∥AB,∵AB∥CD,∴EF∥CD,
∴∠B+∠BEF+∠DEF+∠D=360°,
又∵∠B=α,∠D=β,
∴∠BED=∠BEF+∠DEF=360°-α-β,
故答案为:∠BED=360°-α-β;
(3)猜想:∠BEC=180°-α+β.
证明:过点E作EF∥AB,
则∠BEF=180°-∠B=180°-α,∵AB∥EF,
AB∥CD,∴EF∥CD,∴∠CEF=∠C=β,
∴∠BEC=∠BEF+∠CEF=180°-α+β.
【例题2】探究学习:
(1)感知与填空:如图-①,直线AB∥CD .求证:∠B+∠D=∠BED .
阅读下面的解答过程,井填上适当的理由.
解:延长BE交CD于F,∵AB∥CD(已知),∴∠B=∠1(%// //%)
∵∠1+∠D=∠BED(%// //%),
∴∠B+∠D=∠BED(等量代换).
(2)应用与拓展:如图-②,直线AB∥CD .
若∠B=22°,∠G=35°,∠D=25°,
则∠E+∠F=%////%度.
(3)方法与实践:如图-③,直线AB∥CD .
请探究∠ABE,∠CDE和∠BED之间有怎样
的关系,并证明你的结论.
两直线平行,内错角相等
三角形的外角等于不相邻的两个内角的和
(2)过点G作MG∥AB,
∵AB∥CD,MG∥AB,∴AB∥MG∥CD .
由1知:∠E=∠B+∠MGE,∠F=∠MGF+∠D,
∴∠E+∠F=∠B+∠MGE+∠MGF+∠D
=∠B+∠EGF+∠D
=22°+35°+25°=82°;
故答案为:82°;
(3)∠BED=∠ABE-∠CDE.
证明:延长AB交ED于点F.
∵AB∥CD,
∴∠D=∠BFE.
∵∠ABE=∠BFE+∠BEF,
∴∠BED=∠ABE-∠CDE.
易错1:性质与判定混淆使用
对点练习:已知如图,指出下列推理中的错误,并加以改正.
(1)∵∠1和∠2是内错角,∴∠1=∠2,
(2)∵∠1=∠2,∴AD//BC(两直线平行,内错角相等)
解:(1)错误:内错角不一定相等,
改正:∵∠1和∠2是内错角,DC//AB,
∴∠1=∠2;
(2)错误,
改正:∵∠1=∠2,
∴AB//CD(内错角相等,两直线平行).
易错点2:误用判定
对点练习:如图所示,下列推理及所注理由错误的是(%////%)
A.因为∠1=∠3,所以AB//CD(内错角相等,两直线平行)
B.因为AB//CD,所以∠1=∠3(两直线平行,内错角相等)
C.因为AD//BC,所以∠2=∠4(两直线平行,内错角相等)
D.因为∠2=∠4,所以AD//BC(两直线平行,内错角相等)
D
1.下列说法中,正确的是(%////%)
A.有公共顶点,并且相等的角是对顶角
B.如果两个角不相等,那么它们一定不是对顶角
C.如果两个角相等,那么这两个角是对顶角
D.互补的两个角不可能是对顶角
B
2.如图,某工程队计划把河水引到水池A中,他们先过A点作AB⊥CD,垂足为B,CD为河岸,然后沿AB开渠,可以节约人力、物力和财力,这样设计的数学依据是(%////%)
A.两点之间的所有连线中,线段最短
B.过一点有且只有一条直线垂直于已知直线
C.经过两点有一条直线,并且只有一条直线
D.垂线段最短
D
3.若锐角α的补角是140°,则锐角α的余角是(%////%)
A.30° B.40° C.50° D.60°
C
4.下列作图语句正确的是(%////%)
A.延长线段AB到C,使AB=BC
B.延长射线AB
C.过点A作AB∥CD∥EF
D.作∠AOB的平分线OC
D
5.如图,直线AB、CD相交于点O,OD平分∠BOE,∠AOC=42°,则∠AOE的度数为(%////%)
A.126° B.96°
C.102° D.138°
B
6.如图,下列条件不能判定AB∥CD的是(%////%)
A.∠1=∠2
B.∠D=∠3
C.∠B=∠3
D.∠BAD+∠D=180°
B
7.如图,AB∥CD,AD⊥AC,∠BAD=35°,则∠ACD=(%////%)
A.35° B.45°
C.55° D.70°
C
8.如图,将长方形ABCD沿线段EF折叠到EB′C′F的位置,若∠EFC′=100°,则∠AEB′的度数为(%////%)
A.20° B.30°
C.40° D.50°
A
9.如图,
(1)∵AD//BC(已知),
∴∠B+%// //%=180°(%// //%);
(2)∵∠1=%// //%(已知),
∴AD//BC(%// //%).
∠BAD
∠C
内错角相等,两直线平行
两直线平行,同旁内角互补
10.如图,已知∠1=135°,∠8=45°,直线a与b平行吗?说明理由:
(1)∵∠1=135°(已知),
∴∠2=%//45°//%.
∵∠2=∠%//8//%,
∴a//b(%//同位角相等,两直线平行//%).
(2)∵∠8=45°(已知),
∴∠6=∠8=45°(%//对顶角相等//%).
∵%//∠1//%+%//∠6//%=180°,
∴a//b(%//同旁内角互补,两直线平行//%).
10.如图,已知∠1=135°,∠8=45°,直线a与b平行吗?说明理由:
(1)∵∠1=135°(已知),
∴∠2=%//45°//%.
∵∠2=∠%//8//%,
∴a//b(%//同位角相等,两直线平行//%).
(2)∵∠8=45°(已知),
∴∠6=∠8=45°(%//对顶角相等//%).
∵%//∠1//%+%//∠6//%=180°,
∴a//b(%//同旁内角互补,两直线平行//%).
11.如图,AB//CD,AD与BC相交于点E,∠B=50°,求∠C的度数.
解:∵AB//CD,∠B=50°
∴∠C=∠B=50°.
12.如图,已知△ABC,AD⊥BC于D,E为AB上一点,EF⊥BC于F,DG//BA交CA于G,试说明∠1=∠2.
证明:∵AD⊥BC,EF⊥BC,
∴∠ADF=∠EFB=90°,
∴AD//EF,
∴∠2=∠3,
又∵DG//AB,
∴∠1=∠3,
∴∠1=∠2.
13.如图,直线AD与AB、CD相交于A、D两点,EC与AB、CD分别相交于点E、C,BF与AB、CD分别相交于点B、F,EC与AD相交于点H,BF与AD相交于点G,如果∠1=∠2,∠B=∠C,试说明∠A=∠D .
证明:∵∠2=∠AGB,∠1=∠2,
∴∠1=∠AGB .∴CE//BF,
∴∠B=∠AEC .∵∠B=∠C,
∴∠C=∠AEC .∴AB//CD,
∴∠A=∠D .
14.已知AB∥CD,点M、N分别是AB、CD上的点,点G在AB、CD之间,连接MG、NG.
(1)如图-①,若GM⊥GN,求∠AMG+∠CNG的度数;
(2)如图-②,若点P是CD下方一点,MG平分∠BMP,ND平分∠GNP,已知∠BMG=28°,求∠MGN+∠MPN的度数;
(3)如图-③,若点E是AB上方一点,连接EM、EN,且GM的延长线MF平分∠AME,NE平分∠CNG,2∠MEN+∠MGN=108°,求∠AME的度数(直接写出结果).
解:(1)过点G作GE∥AB,如图1,
∵AB∥CD,∴AB∥GE∥CD,
∴∠AMG=∠MGE,∠CNG=∠NGE,
∴∠AMG+∠CNG=∠MGE+∠NGE=∠MGN,
∵GM⊥GN,∴∠AMG+∠CNG=∠MGN=90°;
(2)过G作GE∥AB,过P作PF∥AB,如图2,
∵AB∥CD,∴AB∥EG∥CD∥FP,
∴∠BMG=∠MGE,∠DNG=∠NGE,
∠BMP=∠FPM,∠FPN=∠DNP,
∵MG平分∠BMP,ND平分∠PNG,
∴∠BMP=2∠BMG=2∠PMG,
∠PND=∠DNG∠PNG,
∴∠MGN+∠MPN=∠MGE+∠NGE+∠FPM-∠FPN
=∠BMG+∠PND+2∠BMG-∠PND
=3∠BMG,
∵∠BMG=28°,∴∠MGN+∠MPN=84°;
(3)∠AME=48°.理由如下:
如图3,过E作EK∥AB,过G作GH∥AB,
∵AB∥CD,∴∠KEM=∠AME,∠KEN=∠CNE,
∠AMF=∠BMG=∠MGH,∠DNG=∠NGH,
∵MF平分∠AME,NE平分∠CNG,
∴∠AME=2∠AMF,∠CNE=∠ENG,
∴∠DNG=180°-2∠CNE,
∴∠MEN=∠KEN-∠KEM=∠CNE-2∠AMF,
∠MGN=∠MGH+∠NGH=∠AMF+180°-2∠CNE,
∵2∠MEN+∠MGN=108°,
∴2(∠CNE-2∠AMF)+(∠AMF+180°-2∠CNE)=108°,
即-3∠AMF+180°=108°,∴∠AMF=24°,
∴∠AME=2∠AMF=48°.
第二章 相交线与平行线
第8课 单元复习
北师大版七年级下册
本套资料以教育部颁布的《数学课程标准(2022)版》为依据,结合新中考改革研究,立足北师大版本教材开发,通过课堂流程的优化设计,内容的层次设计,循序渐进,让不同层次的学生都学有所问,问有所探,探有所获,能力都有不同层次的提高,思维不断生长。
资料简介
【问题1】找出生活中的对顶角、互补的角与互余的角.
【问题2】判断两条直线是否平行,通常有哪些途径?
【问题3】平行线有哪些特征?
【问题4】怎样用尺规作一个角等于已知角?
【问题5】梳理本章内容,用你喜欢的方式(思维导图、列表等)呈现全章知识结构.完成后请和同学交流,并加以完善.
同位角相等,两直线平行;内错角相等,两直线平行;同旁内角互补,两直线平行./
平行线没有交点;
两直线平行,同位角相等;
两直线平行,内错角相等;
两直线平行,同旁内角互补.
【例题1】如图,在直线MN的异侧有A、B两点,按要求画图取点,并注明画图取点的依据.
(1)在直线MN上取一点C,使线段AC最短.依据是%// //%.
(2)在直线MN上取一点D,使线段AD+BD最短.依据是%// //%.
垂线段最短
两点之间,线段最短
【例题2】如图,已知直线AB、CD、EF相交于点O,OG⊥CD,∠BOD=24°.
(1)求∠AOG的度数;
(2)若OC是∠AOE的平分线,那么OG是∠AOF的平分线吗?说明你的理由.
解:(1)∵AB、CD相交于点O,
∴∠AOC=∠BOD=24°,
∵OG⊥CD,∴∠COG=90°,
即∠AOC+∠AOG=90°,
∴∠AOG=90°-∠AOC
=90°-24°=66°;
(2)OG是∠AOF的角平分线,理由如下:
∵OC是∠AOE的角平分线,∴∠AOC=∠COE,
又∵∠DOF=∠COE,∴∠COA=∠DOF,
∵OG⊥CD,∴∠COG=∠DOG=90°,
∴∠AOG=∠GOF,∴OG平分∠AOF.
【例题3】如图,直线AB,CD相交于点O,OD平分∠BOE,OF平分∠AOE.
(1)若∠BOE=58°,∠AOE=122°,判断OF与OD的位置关系,并进行证明
(2)若∠AOC∶∠AOD=1∶5,求∠EOF的度数.
(1)OF⊥OD .
证明:∵OD平分∠BOE,OF平分∠AOE,
∠BOE=58°,∠AOE=122°
∴∠FOE∠AOE=61°,∠EOD∠EOB=29°,
∴∠FOD=∠FOE+∠EOD
(∠AOE+∠EOB)=90°,
∴OF⊥OD;
(2)解:∵∠AOC∶∠AOD=1∶5,∠AOC=∠BOD,
∴∠BOD∶∠AOD=1∶5,
∵∠AOD+∠BOD=180°,
∴∠BOD=30°,∠AOD=150°,
∵OD平分∠BOE,OF平分∠AOE,
∴∠BOE=2∠BOD=60°,∠EOF∠AOE.
∵∠AOE+∠BOE=180°,
∴∠AOE=120°,∴∠EOF=60°.
【例题1】如图,∠B的同位角可以是(%////%)
A.∠1 B.∠2
C.∠3 D.∠4
D
【例题2】如图,由下列条件可以判定图中哪两条直线平行,说明理由:
(1)若∠1=∠B,则%// //%;
(2)若∠3=∠4,则%// //%;
(3)若∠1=∠D,则%// //%;
(4)若∠DAB+∠B=180°,则%// //%.
AD//BC
AB//CD
AB//CD
AD//BC
【例题3】如图,已知∠AEM=∠DGN,求证:AB//CD .
证明:∵∠AEM=∠DGN,∠DGN=∠CGM,
∴∠AEM=∠CGM,
∴AB//CD(同位角相等,两直线平行)/
【例题1】(1)如图,BE//CD,∠C=∠E,试说明∠A=∠ADE.
证明:∵BE//CD,
∴∠C=∠1(两直线平行,同位角相等),
∵∠C=∠E,∴∠1=∠E,
∴AC//DE(内错角相等,两直线平行),
∴∠A=∠ADE.
(2)已知:如图,∠1=∠2,∠C=∠D,求证:∠DBC+∠D=180°.
证明:∵∠1=∠2(已知),又∠1=∠DMN(对顶角相等),
∴∠2=∠DMN(等量代换),
∴DB//EC(同位角相等,两直线平行),
∴∠DBC+∠C=180°(两直线平行,同旁内角互补).
∵∠C=∠D(已知),∴∠DBC+∠D=180°(等量代换).
【例题1】尺规作图是指(%////%)
A.用直尺和圆规作图
B.用直尺规范作图
C.用刻度尺和圆规作图
D.用没有刻度的直尺和圆规作图
【例题2】下列各说法一定成立的是(%////%)
A.画直线AB=10厘米
B.已知A、B、C三点,过这三点画一条直线
C.画射线OB=10厘米
D.过直线AB外一点画一条直线和直线AB平行
D
D
【例题1】直线AB∥CD,E为直线AB、CD之间的一点,完成以下问题:
(1)如图-①,若∠B=15°,∠BED=90°,则∠D=%// //%;
(2)如图-②,若∠B=α,∠D=β,求出∠BED的度数(用a、β表示);
(3)如图-③,若∠B=α,∠C=β,则a、β与∠BEC之间有什么等量关系?请猜想证明.
解:(1)过E作EF∥AB,∵AB∥CD,∴EF∥CD,
∵∠B=15°,∴∠BEF=15°,
又∵∠BED=90°,∴∠DEF=75°,
∵EF∥CD,∴∠D=75°,故答案为:75°;
(2)过E作EF∥AB,∵AB∥CD,∴EF∥CD,
∴∠B+∠BEF+∠DEF+∠D=360°,
又∵∠B=α,∠D=β,
∴∠BED=∠BEF+∠DEF=360°-α-β,
故答案为:∠BED=360°-α-β;
(3)猜想:∠BEC=180°-α+β.
证明:过点E作EF∥AB,
则∠BEF=180°-∠B=180°-α,∵AB∥EF,
AB∥CD,∴EF∥CD,∴∠CEF=∠C=β,
∴∠BEC=∠BEF+∠CEF=180°-α+β.
【例题2】探究学习:
(1)感知与填空:如图-①,直线AB∥CD .求证:∠B+∠D=∠BED .
阅读下面的解答过程,井填上适当的理由.
解:延长BE交CD于F,∵AB∥CD(已知),∴∠B=∠1(%// //%)
∵∠1+∠D=∠BED(%// //%),
∴∠B+∠D=∠BED(等量代换).
(2)应用与拓展:如图-②,直线AB∥CD .
若∠B=22°,∠G=35°,∠D=25°,
则∠E+∠F=%////%度.
(3)方法与实践:如图-③,直线AB∥CD .
请探究∠ABE,∠CDE和∠BED之间有怎样
的关系,并证明你的结论.
两直线平行,内错角相等
三角形的外角等于不相邻的两个内角的和
(2)过点G作MG∥AB,
∵AB∥CD,MG∥AB,∴AB∥MG∥CD .
由1知:∠E=∠B+∠MGE,∠F=∠MGF+∠D,
∴∠E+∠F=∠B+∠MGE+∠MGF+∠D
=∠B+∠EGF+∠D
=22°+35°+25°=82°;
故答案为:82°;
(3)∠BED=∠ABE-∠CDE.
证明:延长AB交ED于点F.
∵AB∥CD,
∴∠D=∠BFE.
∵∠ABE=∠BFE+∠BEF,
∴∠BED=∠ABE-∠CDE.
易错1:性质与判定混淆使用
对点练习:已知如图,指出下列推理中的错误,并加以改正.
(1)∵∠1和∠2是内错角,∴∠1=∠2,
(2)∵∠1=∠2,∴AD//BC(两直线平行,内错角相等)
解:(1)错误:内错角不一定相等,
改正:∵∠1和∠2是内错角,DC//AB,
∴∠1=∠2;
(2)错误,
改正:∵∠1=∠2,
∴AB//CD(内错角相等,两直线平行).
易错点2:误用判定
对点练习:如图所示,下列推理及所注理由错误的是(%////%)
A.因为∠1=∠3,所以AB//CD(内错角相等,两直线平行)
B.因为AB//CD,所以∠1=∠3(两直线平行,内错角相等)
C.因为AD//BC,所以∠2=∠4(两直线平行,内错角相等)
D.因为∠2=∠4,所以AD//BC(两直线平行,内错角相等)
D
1.下列说法中,正确的是(%////%)
A.有公共顶点,并且相等的角是对顶角
B.如果两个角不相等,那么它们一定不是对顶角
C.如果两个角相等,那么这两个角是对顶角
D.互补的两个角不可能是对顶角
B
2.如图,某工程队计划把河水引到水池A中,他们先过A点作AB⊥CD,垂足为B,CD为河岸,然后沿AB开渠,可以节约人力、物力和财力,这样设计的数学依据是(%////%)
A.两点之间的所有连线中,线段最短
B.过一点有且只有一条直线垂直于已知直线
C.经过两点有一条直线,并且只有一条直线
D.垂线段最短
D
3.若锐角α的补角是140°,则锐角α的余角是(%////%)
A.30° B.40° C.50° D.60°
C
4.下列作图语句正确的是(%////%)
A.延长线段AB到C,使AB=BC
B.延长射线AB
C.过点A作AB∥CD∥EF
D.作∠AOB的平分线OC
D
5.如图,直线AB、CD相交于点O,OD平分∠BOE,∠AOC=42°,则∠AOE的度数为(%////%)
A.126° B.96°
C.102° D.138°
B
6.如图,下列条件不能判定AB∥CD的是(%////%)
A.∠1=∠2
B.∠D=∠3
C.∠B=∠3
D.∠BAD+∠D=180°
B
7.如图,AB∥CD,AD⊥AC,∠BAD=35°,则∠ACD=(%////%)
A.35° B.45°
C.55° D.70°
C
8.如图,将长方形ABCD沿线段EF折叠到EB′C′F的位置,若∠EFC′=100°,则∠AEB′的度数为(%////%)
A.20° B.30°
C.40° D.50°
A
9.如图,
(1)∵AD//BC(已知),
∴∠B+%// //%=180°(%// //%);
(2)∵∠1=%// //%(已知),
∴AD//BC(%// //%).
∠BAD
∠C
内错角相等,两直线平行
两直线平行,同旁内角互补
10.如图,已知∠1=135°,∠8=45°,直线a与b平行吗?说明理由:
(1)∵∠1=135°(已知),
∴∠2=%//45°//%.
∵∠2=∠%//8//%,
∴a//b(%//同位角相等,两直线平行//%).
(2)∵∠8=45°(已知),
∴∠6=∠8=45°(%//对顶角相等//%).
∵%//∠1//%+%//∠6//%=180°,
∴a//b(%//同旁内角互补,两直线平行//%).
10.如图,已知∠1=135°,∠8=45°,直线a与b平行吗?说明理由:
(1)∵∠1=135°(已知),
∴∠2=%//45°//%.
∵∠2=∠%//8//%,
∴a//b(%//同位角相等,两直线平行//%).
(2)∵∠8=45°(已知),
∴∠6=∠8=45°(%//对顶角相等//%).
∵%//∠1//%+%//∠6//%=180°,
∴a//b(%//同旁内角互补,两直线平行//%).
11.如图,AB//CD,AD与BC相交于点E,∠B=50°,求∠C的度数.
解:∵AB//CD,∠B=50°
∴∠C=∠B=50°.
12.如图,已知△ABC,AD⊥BC于D,E为AB上一点,EF⊥BC于F,DG//BA交CA于G,试说明∠1=∠2.
证明:∵AD⊥BC,EF⊥BC,
∴∠ADF=∠EFB=90°,
∴AD//EF,
∴∠2=∠3,
又∵DG//AB,
∴∠1=∠3,
∴∠1=∠2.
13.如图,直线AD与AB、CD相交于A、D两点,EC与AB、CD分别相交于点E、C,BF与AB、CD分别相交于点B、F,EC与AD相交于点H,BF与AD相交于点G,如果∠1=∠2,∠B=∠C,试说明∠A=∠D .
证明:∵∠2=∠AGB,∠1=∠2,
∴∠1=∠AGB .∴CE//BF,
∴∠B=∠AEC .∵∠B=∠C,
∴∠C=∠AEC .∴AB//CD,
∴∠A=∠D .
14.已知AB∥CD,点M、N分别是AB、CD上的点,点G在AB、CD之间,连接MG、NG.
(1)如图-①,若GM⊥GN,求∠AMG+∠CNG的度数;
(2)如图-②,若点P是CD下方一点,MG平分∠BMP,ND平分∠GNP,已知∠BMG=28°,求∠MGN+∠MPN的度数;
(3)如图-③,若点E是AB上方一点,连接EM、EN,且GM的延长线MF平分∠AME,NE平分∠CNG,2∠MEN+∠MGN=108°,求∠AME的度数(直接写出结果).
解:(1)过点G作GE∥AB,如图1,
∵AB∥CD,∴AB∥GE∥CD,
∴∠AMG=∠MGE,∠CNG=∠NGE,
∴∠AMG+∠CNG=∠MGE+∠NGE=∠MGN,
∵GM⊥GN,∴∠AMG+∠CNG=∠MGN=90°;
(2)过G作GE∥AB,过P作PF∥AB,如图2,
∵AB∥CD,∴AB∥EG∥CD∥FP,
∴∠BMG=∠MGE,∠DNG=∠NGE,
∠BMP=∠FPM,∠FPN=∠DNP,
∵MG平分∠BMP,ND平分∠PNG,
∴∠BMP=2∠BMG=2∠PMG,
∠PND=∠DNG∠PNG,
∴∠MGN+∠MPN=∠MGE+∠NGE+∠FPM-∠FPN
=∠BMG+∠PND+2∠BMG-∠PND
=3∠BMG,
∵∠BMG=28°,∴∠MGN+∠MPN=84°;
(3)∠AME=48°.理由如下:
如图3,过E作EK∥AB,过G作GH∥AB,
∵AB∥CD,∴∠KEM=∠AME,∠KEN=∠CNE,
∠AMF=∠BMG=∠MGH,∠DNG=∠NGH,
∵MF平分∠AME,NE平分∠CNG,
∴∠AME=2∠AMF,∠CNE=∠ENG,
∴∠DNG=180°-2∠CNE,
∴∠MEN=∠KEN-∠KEM=∠CNE-2∠AMF,
∠MGN=∠MGH+∠NGH=∠AMF+180°-2∠CNE,
∵2∠MEN+∠MGN=108°,
∴2(∠CNE-2∠AMF)+(∠AMF+180°-2∠CNE)=108°,
即-3∠AMF+180°=108°,∴∠AMF=24°,
∴∠AME=2∠AMF=48°.
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
