【备课参考】2015秋冀教版数学八上课件17.2直角三角形(共16张PPT)
文档属性
| 名称 | 【备课参考】2015秋冀教版数学八上课件17.2直角三角形(共16张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 214.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-10-02 14:33:11 | ||
图片预览


文档简介
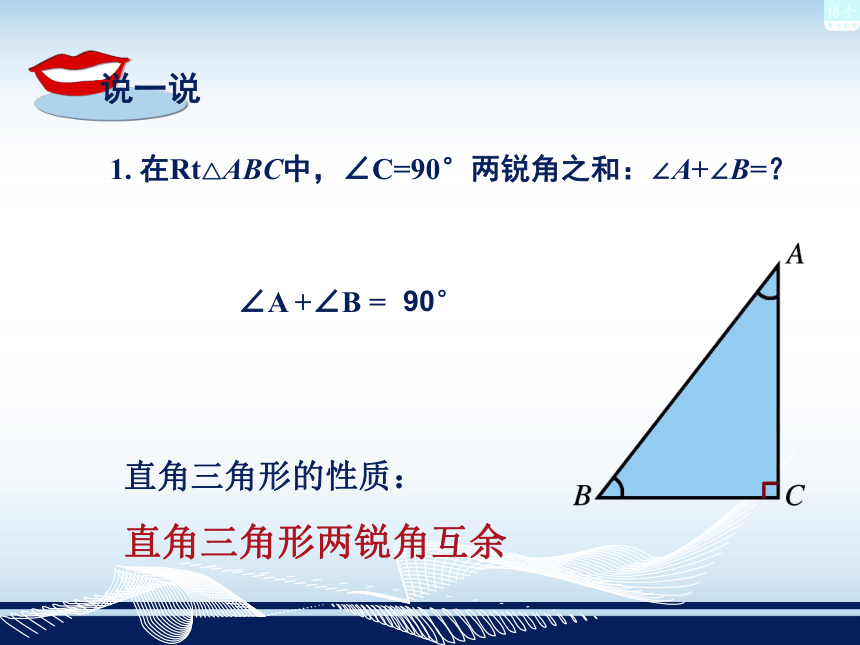
课件16张PPT。直 角 三 角 形17.217.2 直角三角形的性质和判定 1. 在Rt△ABC中,∠C=90°两锐角之和:∠A+∠B=?∠A +∠B = 90°直角三角形的性质:
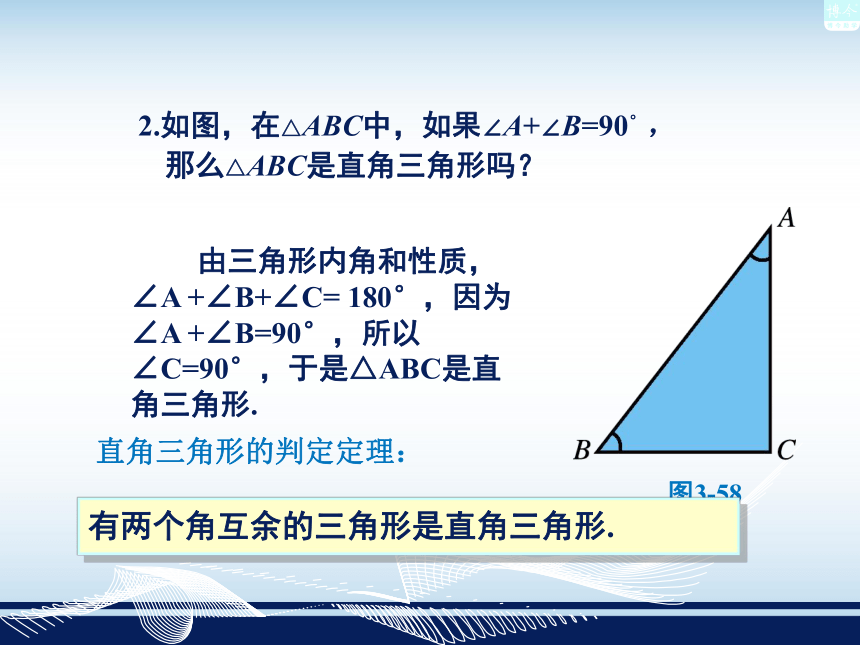
直角三角形两锐角互余 2.如图,在△ABC中,如果∠A+∠B=90°,
那么△ABC是直角三角形吗?图3-58 由三角形内角和性质,∠A +∠B+∠C= 180°,因为∠A +∠B=90°,所以∠C=90°,于是△ABC是直角三角形.
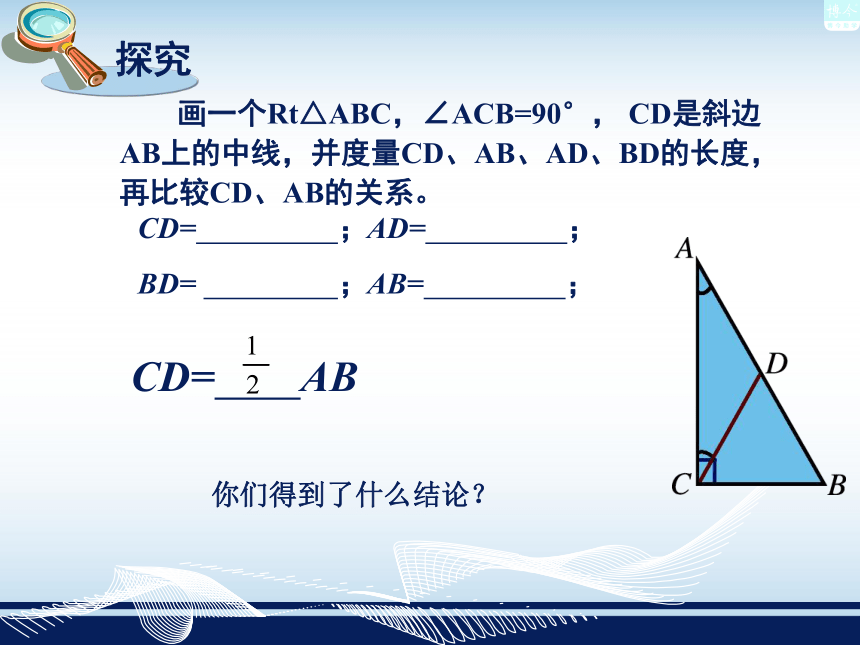
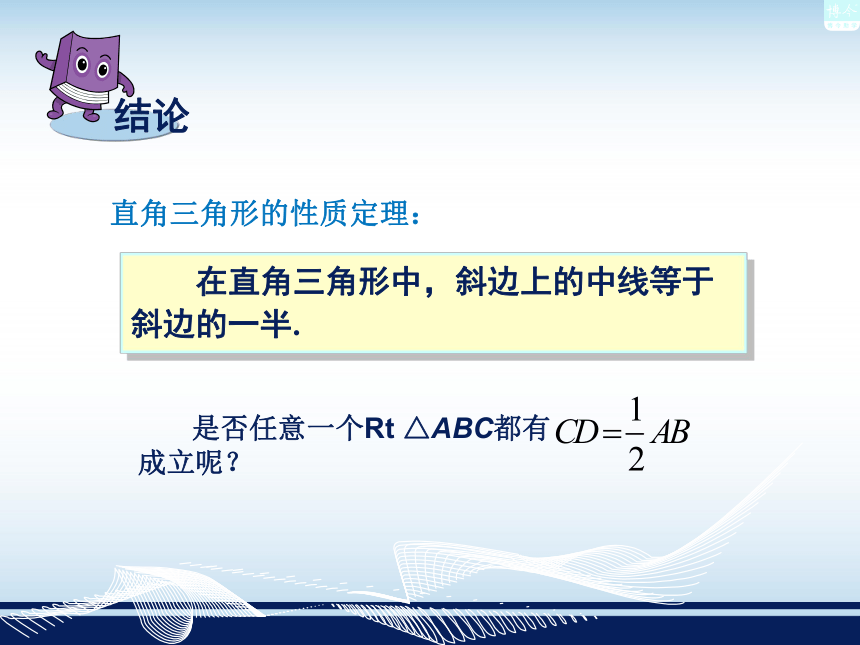
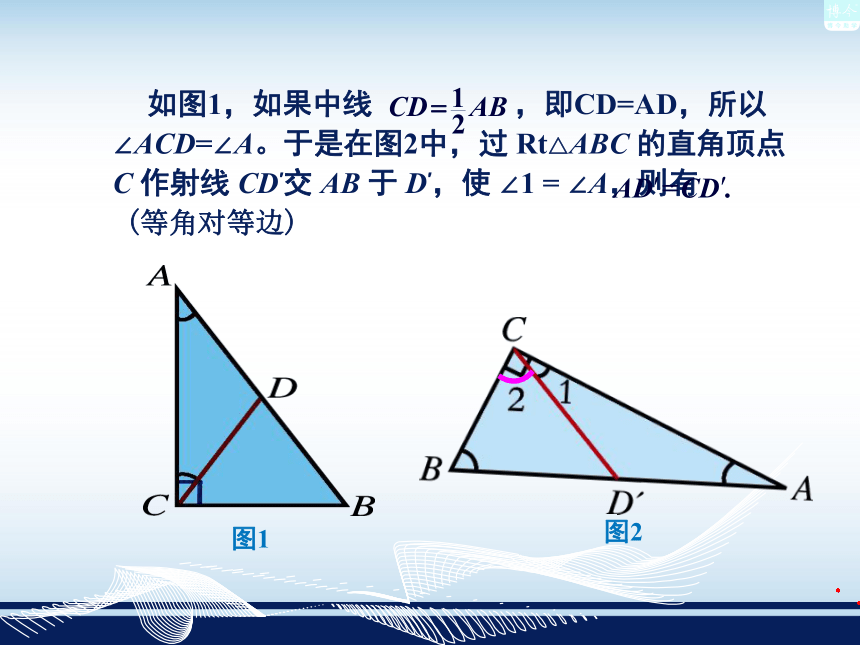
有两个角互余的三角形是直角三角形. 直角三角形的判定定理: 画一个Rt△ABC,∠ACB=90°, CD是斜边AB上的中线,并度量CD、AB、AD、BD的长度,再比较CD、AB的关系。CD= ;AD= ;BD= ;AB= ;CD= AB你们得到了什么结论? 在直角三角形中,斜边上的中线等于斜边的一半. 直角三角形的性质定理:图2图1直角三角形两个角等于90° 又∵∠A +∠B = 90° ( )
∠1 +∠2 = 90°∴ ∠B =∠2∴ D′是斜边AB的中点例1 如果三角形一边上的中线等于这条边的一半,
求证:这个三角形是直角三角形.
证明:∴ ∠1=∠A等边对等角∠2=∠B ( )又 ∵ ∠A+∠B+∠ACB =180°(三角形 内角和的性质)即∠A+∠B+∠1+∠2=180°∴ 2(∠A+∠B)=180°∴ ∠A+∠B =90°∴ △ABC是直角三角形( ) 有两个角互余的三角形是直角三角形三角形一边上的中线等于这条边的一半的
三角形是直角三角形. 直角三角形的判定定理:(1)在Rt△ABC中,有一个锐角为52度,那么另一个锐角度数为???????; (2)在Rt△ABC中,∠C=90度,∠A -∠B =30度,那么∠A=?????? ,∠B=?????? ;(3)在△ABC中, ∠C=90 °,CE是AB边上的中线,那么与CE相等的线段是_____,与∠A相等的角是_____,若∠A=35°,那么∠ECB= ______.(4)在直角三角形中,斜边及其中线之和为6,那么该三角形的斜边长为________. 1.本节课我们学习了哪些内容?1:直角三角形两锐角互余;2:在直角三角形中,斜边上的中线等于斜边的一半;
……2:三角形一边上的中线等于这条边的一半的三角形是直角三角形;
1:有一个角内角等于90°的三角形是直角三角形。3:有两个角互余的三角形是直角三角形;……1、如图,在Rt△ABC中,∠ACB=90度,CD是斜边AB上的高,那么, 与∠B互余的角有????????,与∠A互余的角有????????,与∠B相等的角有????????? ,与∠A相等的角有?????????.作业:
2、如图,在△ABC中,AD⊥BC,E、F分别是AB、AC的中点,且DE=DF.谢谢观赏!请多多指教 提示:延长CD,使得CD=DE,连结BE, 证明:在直角三角形中,斜边上的中线等于斜边的一半。
直角三角形两锐角互余 2.如图,在△ABC中,如果∠A+∠B=90°,
那么△ABC是直角三角形吗?图3-58 由三角形内角和性质,∠A +∠B+∠C= 180°,因为∠A +∠B=90°,所以∠C=90°,于是△ABC是直角三角形.
有两个角互余的三角形是直角三角形. 直角三角形的判定定理: 画一个Rt△ABC,∠ACB=90°, CD是斜边AB上的中线,并度量CD、AB、AD、BD的长度,再比较CD、AB的关系。CD= ;AD= ;BD= ;AB= ;CD= AB你们得到了什么结论? 在直角三角形中,斜边上的中线等于斜边的一半. 直角三角形的性质定理:图2图1直角三角形两个角等于90° 又∵∠A +∠B = 90° ( )
∠1 +∠2 = 90°∴ ∠B =∠2∴ D′是斜边AB的中点例1 如果三角形一边上的中线等于这条边的一半,
求证:这个三角形是直角三角形.
证明:∴ ∠1=∠A等边对等角∠2=∠B ( )又 ∵ ∠A+∠B+∠ACB =180°(三角形 内角和的性质)即∠A+∠B+∠1+∠2=180°∴ 2(∠A+∠B)=180°∴ ∠A+∠B =90°∴ △ABC是直角三角形( ) 有两个角互余的三角形是直角三角形三角形一边上的中线等于这条边的一半的
三角形是直角三角形. 直角三角形的判定定理:(1)在Rt△ABC中,有一个锐角为52度,那么另一个锐角度数为???????; (2)在Rt△ABC中,∠C=90度,∠A -∠B =30度,那么∠A=?????? ,∠B=?????? ;(3)在△ABC中, ∠C=90 °,CE是AB边上的中线,那么与CE相等的线段是_____,与∠A相等的角是_____,若∠A=35°,那么∠ECB= ______.(4)在直角三角形中,斜边及其中线之和为6,那么该三角形的斜边长为________. 1.本节课我们学习了哪些内容?1:直角三角形两锐角互余;2:在直角三角形中,斜边上的中线等于斜边的一半;
……2:三角形一边上的中线等于这条边的一半的三角形是直角三角形;
1:有一个角内角等于90°的三角形是直角三角形。3:有两个角互余的三角形是直角三角形;……1、如图,在Rt△ABC中,∠ACB=90度,CD是斜边AB上的高,那么, 与∠B互余的角有????????,与∠A互余的角有????????,与∠B相等的角有????????? ,与∠A相等的角有?????????.作业:
2、如图,在△ABC中,AD⊥BC,E、F分别是AB、AC的中点,且DE=DF.谢谢观赏!请多多指教 提示:延长CD,使得CD=DE,连结BE, 证明:在直角三角形中,斜边上的中线等于斜边的一半。
同课章节目录
- 第十二章 分式和分式方程
- 12.1 分式
- 12.2 分式的乘除
- 12.3 分式的加减
- 12.4 分式方程
- 12.5 分式方程的应用
- 第十三章 全等三角形
- 13.1 命题与证明
- 13.2 全等图形
- 13.3 全等三角形的判定
- 13.4 三角形的尺规作图
- 第十四章 实数
- 14.1 平方根
- 14.2 立方根
- 14.3 实数
- 14.4 近似数
- 14.5 用计算器求平方根与立方根
- 第十五章 二次根式
- 15.1 二次根式
- 15.2 二次根式的乘除
- 15.3 二次根式的加减
- 15.4 二次根式的混合
- 第十六章 轴对称和中心对称
- 16.1 轴对称
- 16.2 线段的垂直平分
- 16.3 角的平分线
- 16.4 中心对称图形
- 16.5 利用图形的平移、旋转和轴对称设计图案
- 第十七章 特殊三角形
- 17.1 等腰三角形
- 17.2 直角三角形
- 17.3 勾股定理
- 17.4 直角三角形全等的判定
- 17.5 反证法
