第九章 图形的相似 专题3 相似三角形的四大模型(含答案)
文档属性
| 名称 | 第九章 图形的相似 专题3 相似三角形的四大模型(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 4.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-30 14:30:57 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
第九章 图形的相似
专题3 相似三角形的四大模型
模型1 A 字型
【模型解读】两个三角形若有“一个公共角 + 一对等角”,则出现“A”字型相似,没有说明对应角的关系时,需分∠AED=∠B 或∠AED =∠C两种情况讨论.
模型展示 结论
条件:DE∥BC. 结论:△AED∽△ACB.
条件:∠AED=∠B 或 结论:△AED∽△ABC.
条件:∠D=∠B, ∠DAB=∠CAE. 结论:△AED∽△ACB.
1.如图,已知∠ACD =∠B, BD=5,AD=4,求AC 的长.
模型2 8 字型
【模型解读】两个三角形若有“一对对顶角 + 一对等角”,则出现“8”字型相似.没有说明对应角的关系时,需分 或 两种情况讨论.
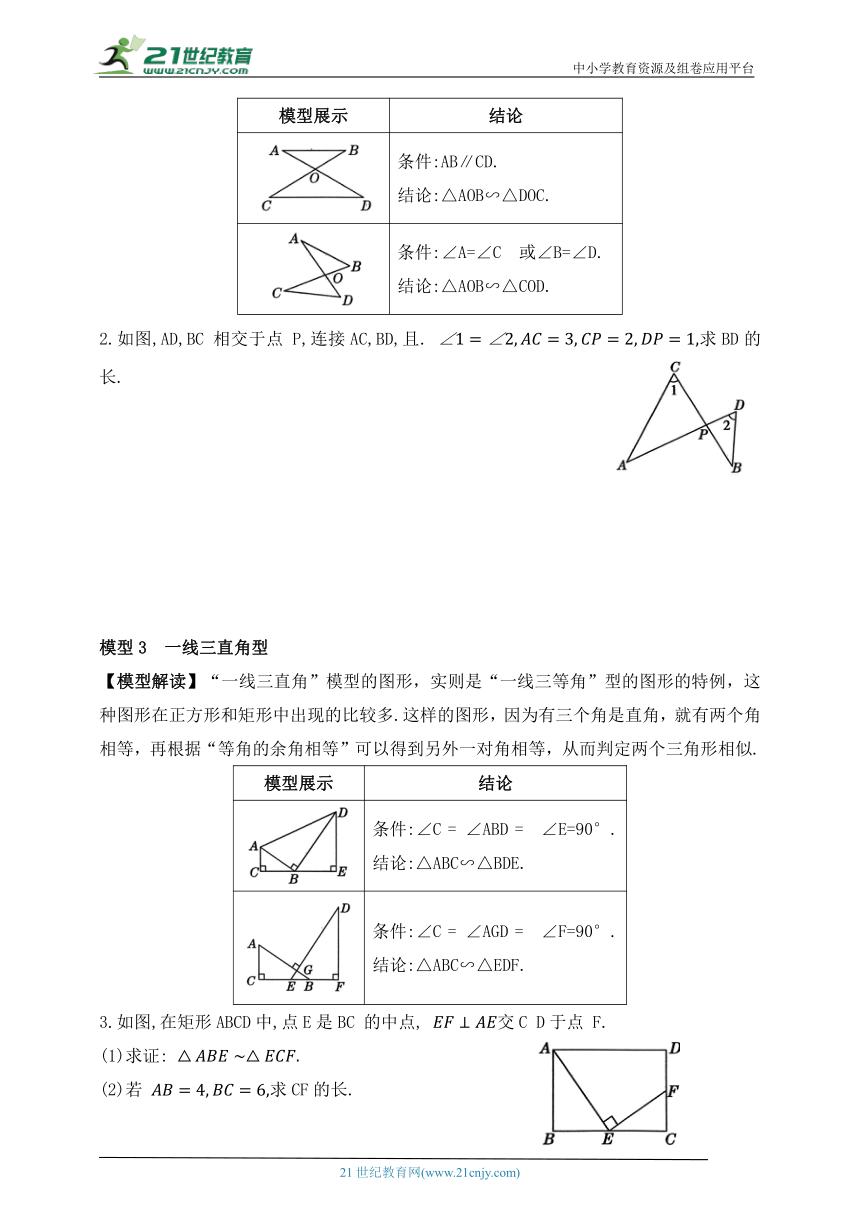
模型展示 结论
条件:AB∥CD. 结论:△AOB∽△DOC.
条件:∠A=∠C 或∠B=∠D. 结论:△AOB∽△COD.
2.如图,AD,BC 相交于点 P,连接AC,BD,且. 求BD的长.
模型3 一线三直角型
【模型解读】“一线三直角”模型的图形,实则是“一线三等角”型的图形的特例,这种图形在正方形和矩形中出现的比较多.这样的图形,因为有三个角是直角,就有两个角相等,再根据“等角的余角相等”可以得到另外一对角相等,从而判定两个三角形相似.
模型展示 结论
条件:∠C = ∠ABD = ∠E=90°. 结论:△ABC∽△BDE.
条件:∠C = ∠AGD = ∠F=90°. 结论:△ABC∽△EDF.
3.如图,在矩形ABCD中,点E是BC 的中点, 交C D于点 F.
(1)求证:
(2)若 求CF的长.
模型4 共角共边型
【模型解读】共角共边型有一个“公共角”,再有一个角相等或夹这个公共角的两边对应成比例就可以判定这两个三角形相似.“双垂线”型是其特例.
模型展示 结论
条件:∠C=∠ABD或. 结论:△ABD∽△ACB.
条件:CD⊥AB,AC⊥BC. 结论:①△ADC∽△CDB; ②△ADC∽△ACB; ③△CDB∽△ACB.
4.如图,E 为 AD 上一点,若求证:CD·
参考答案
1.【解】∵
即 解得. ,即AC 的长是6.
2. 【 解】
∴BD的长为
3.(1)【证明】∵ 四边形 ABCD 是矩形,
(2)【解】∵ E 是 BC 的中点,
即
4.【证明】∵
∽△
AD·AE.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第九章 图形的相似
专题3 相似三角形的四大模型
模型1 A 字型
【模型解读】两个三角形若有“一个公共角 + 一对等角”,则出现“A”字型相似,没有说明对应角的关系时,需分∠AED=∠B 或∠AED =∠C两种情况讨论.
模型展示 结论
条件:DE∥BC. 结论:△AED∽△ACB.
条件:∠AED=∠B 或 结论:△AED∽△ABC.
条件:∠D=∠B, ∠DAB=∠CAE. 结论:△AED∽△ACB.
1.如图,已知∠ACD =∠B, BD=5,AD=4,求AC 的长.
模型2 8 字型
【模型解读】两个三角形若有“一对对顶角 + 一对等角”,则出现“8”字型相似.没有说明对应角的关系时,需分 或 两种情况讨论.
模型展示 结论
条件:AB∥CD. 结论:△AOB∽△DOC.
条件:∠A=∠C 或∠B=∠D. 结论:△AOB∽△COD.
2.如图,AD,BC 相交于点 P,连接AC,BD,且. 求BD的长.
模型3 一线三直角型
【模型解读】“一线三直角”模型的图形,实则是“一线三等角”型的图形的特例,这种图形在正方形和矩形中出现的比较多.这样的图形,因为有三个角是直角,就有两个角相等,再根据“等角的余角相等”可以得到另外一对角相等,从而判定两个三角形相似.
模型展示 结论
条件:∠C = ∠ABD = ∠E=90°. 结论:△ABC∽△BDE.
条件:∠C = ∠AGD = ∠F=90°. 结论:△ABC∽△EDF.
3.如图,在矩形ABCD中,点E是BC 的中点, 交C D于点 F.
(1)求证:
(2)若 求CF的长.
模型4 共角共边型
【模型解读】共角共边型有一个“公共角”,再有一个角相等或夹这个公共角的两边对应成比例就可以判定这两个三角形相似.“双垂线”型是其特例.
模型展示 结论
条件:∠C=∠ABD或. 结论:△ABD∽△ACB.
条件:CD⊥AB,AC⊥BC. 结论:①△ADC∽△CDB; ②△ADC∽△ACB; ③△CDB∽△ACB.
4.如图,E 为 AD 上一点,若求证:CD·
参考答案
1.【解】∵
即 解得. ,即AC 的长是6.
2. 【 解】
∴BD的长为
3.(1)【证明】∵ 四边形 ABCD 是矩形,
(2)【解】∵ E 是 BC 的中点,
即
4.【证明】∵
∽△
AD·AE.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
