第九章 图形的相似 5 相似三角形判定定理的证明(含答案)
文档属性
| 名称 | 第九章 图形的相似 5 相似三角形判定定理的证明(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 4.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-30 13:19:30 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
第九章 图形的相似
5 相似三角形判定定理的证明
基 础 练
练点 用适当的方法判定两个三角形相似
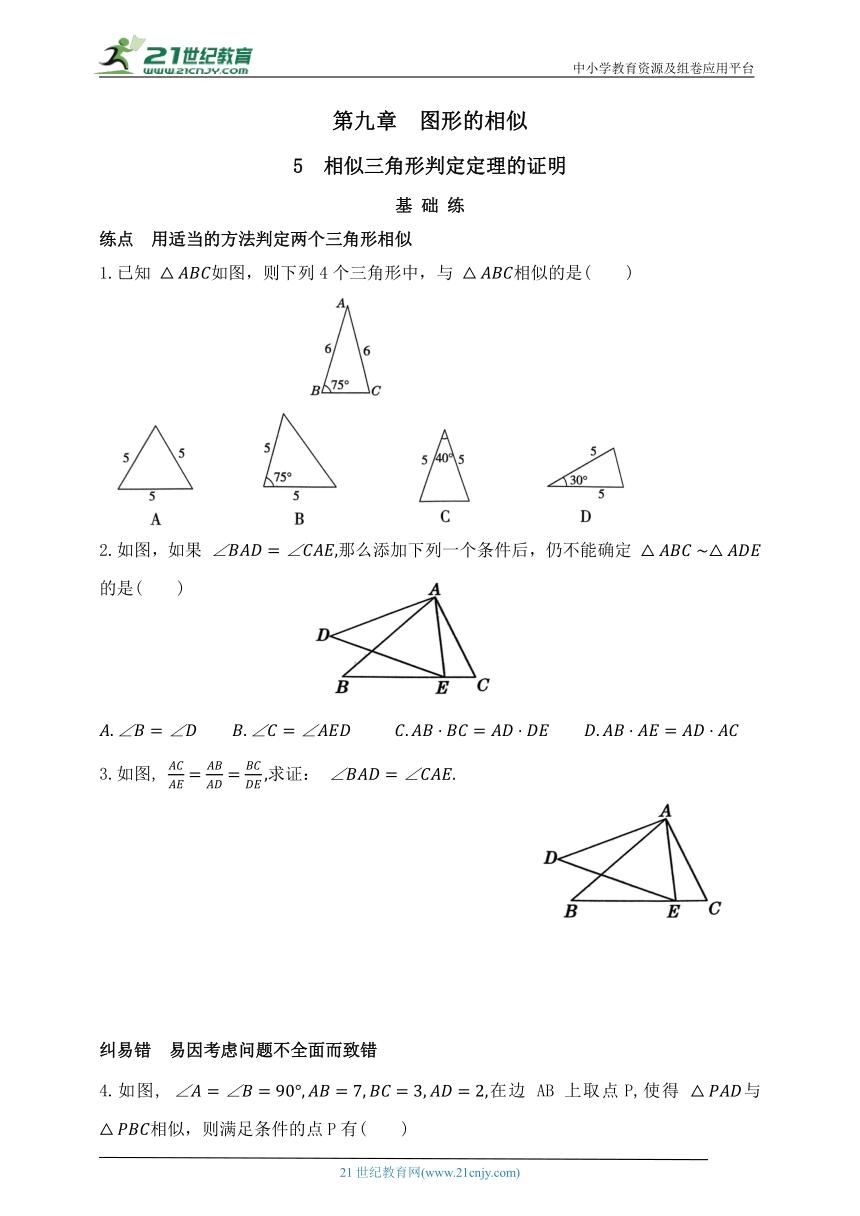
1.已知 如图,则下列4个三角形中,与 相似的是( )
2.如图,如果 那么添加下列一个条件后,仍不能确定 的是( )
3.如图, 求证:
纠易错 易因考虑问题不全面而致错
4.如图, 在边 AB 上取点P,使得 与 相似,则满足条件的点P有( )
A.1个 B.2个 C.3 个 D.0个
提 升 练
5.如图,在正方形ABCD 中,E 是 BC 的中点, F 是 CD上一点,且下列结论: ②△ABE∽△AEF;③AE⊥ EF;④△ADF∽其中正确的个数为( )
A.1 B.2 C.3 D.4
第5 题图 第6题图
6.如图,在 中, ,过AB 上一点 D 作直线 DF 交 AC 于点F,使所得的三角形与原三角形相似,这样的直线可以作出的条数为__________.
7.如图,已知点 F 在 AB 上,且AF:点D是BC延长线上一点,2:1,连接 FD与AC 交于点 N,求 的值.
8.在矩形 ABCD 中,,E 为AB 边上一点,连接DE,过点C作垂足为 F.
(1)求证:
(2)若设 求y 与 x 的函数表达式.
9.如图,点P在的外部,连接AP,BP,在 的外部分别作连接PQ.
(1)求证:
(2)判断 与 的数量关系,并说明理由.
10.如图,将 绕点 A 逆时针旋转得到,ED 的延长线与BC 相交于点 F,连接AF,EC.
(1)求证: ∥
(2)求证:
11.如图①,点P是菱形ABCD 的对角线 BD 上一点,连接CP并延长,交AD于点 E,交 BA 的延长线于点 F.
(1)求证:
(2)如图②,连接 AC 交 BD 于 O,连接OE,若求证:
参考答案
1. D 【点拨】∵ 由题图可知, A.三角形各角的度数都是B.三角 形各角的度 数分别为 C.三角形各角的度数分别为 D.三角形各角的度数分别为 只D选项中三角形各角的度数与题干中三角形各角的度数相等.
2. C 【点拨】∵A.若添加 可用两角对应相等的两个三角形相似,证明△ABC∽ △ADE;B. 若添加∠C =∠AED,可用两角对应相等的两个三角形相似,证明△ABC∽△ADE;C.若添加AB·BC=AD·DE,不能证明△ABC∽△ADE;D.若添加AB·AE=AD·AC,可用两边对应成比例,且夹角相等的两个三角形相似,证明△ABC∽△ADE.
3.【证明】 ∴∠BAC=∠DAE, ∴∠EAD-∠EAB =∠BAC-∠EAB,∴∠BAD=∠CAE.
4. C 【点拨】∵∠A =∠B=90°,若△PAD与△PBC相似,可分两种情况:①若△APD∽△BPC,则 解得 AP =2.8. ②若△APD∽△BCP,则 解得AP=1 或6.∴满足条件的AP长为2.8 或1 或6,∴满足条件的点 P有3 个.
5. B 【点拨】∵在正方形ABCD 中,E是 BC 的中点,F是CD上一点,且∴②③正确.
6.2 条 【点拨】如图,①作 ②作 ∥因此共有 2 种作法.
【解】方法一:如图①,连接CF,AD. ∵ AF:BF =∥
方法二:如图②,过点 F 作. 交AC 于点 E,即 ∥
8.(1)【证明】∵ 四边形ABCD 是矩形,
(2)【解】 ∵四边形ABCD为矩形,
9.(1)【证明】∵∠1=∠BAC,∴∠1 +∠PAC=∠BAC+∠PAC,∴∠CAQ=∠BAP.∵ ∠2 =∠ABP,
(2) 【解】∠PQA = ∠ACB. 理由: ∵ AC ·AP =
∵∠1 =∠BAC,∴△APQ∽△ABC,∴∠PQA =∠ACB.
10.【证明】(1)∵ △ABC 绕点 A 逆时针旋转60°得到△ADE,∴△ABC≌△ADE.∴∠EAC=∠BAC,AC=AE.∵∠EAC=60°,∴△AEC 为等边三角形, ∠BAC=60°.∴∠ACE=60°=∠BAC,∴AB∥EC.
(2)∵△ABC≌△ADE,∴ ∠AED=∠ACB.又∵∠ADE=∠FDC,∴ △ADE∽△FDC.又∵∠ADF=∠EDC,∴△DAF∽△DEC.
11.【证明】(1)∵ 四边形 ABCD 是菱形,∴ AD= CD,∠CDP =∠ADP,CD∥AB.
在△CDP和△ADP中,
∴△CDP≌△ADP(SAS),∴PC=PA,∠DCP=∠DAP.
∵∥
∥.
∵四边形 ABCD 是菱形,
点方法 题(1) 中的相似三角形是常见的共边共角型, 一般用“两角相等的两个三角形相似”证明相似.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第九章 图形的相似
5 相似三角形判定定理的证明
基 础 练
练点 用适当的方法判定两个三角形相似
1.已知 如图,则下列4个三角形中,与 相似的是( )
2.如图,如果 那么添加下列一个条件后,仍不能确定 的是( )
3.如图, 求证:
纠易错 易因考虑问题不全面而致错
4.如图, 在边 AB 上取点P,使得 与 相似,则满足条件的点P有( )
A.1个 B.2个 C.3 个 D.0个
提 升 练
5.如图,在正方形ABCD 中,E 是 BC 的中点, F 是 CD上一点,且下列结论: ②△ABE∽△AEF;③AE⊥ EF;④△ADF∽其中正确的个数为( )
A.1 B.2 C.3 D.4
第5 题图 第6题图
6.如图,在 中, ,过AB 上一点 D 作直线 DF 交 AC 于点F,使所得的三角形与原三角形相似,这样的直线可以作出的条数为__________.
7.如图,已知点 F 在 AB 上,且AF:点D是BC延长线上一点,2:1,连接 FD与AC 交于点 N,求 的值.
8.在矩形 ABCD 中,,E 为AB 边上一点,连接DE,过点C作垂足为 F.
(1)求证:
(2)若设 求y 与 x 的函数表达式.
9.如图,点P在的外部,连接AP,BP,在 的外部分别作连接PQ.
(1)求证:
(2)判断 与 的数量关系,并说明理由.
10.如图,将 绕点 A 逆时针旋转得到,ED 的延长线与BC 相交于点 F,连接AF,EC.
(1)求证: ∥
(2)求证:
11.如图①,点P是菱形ABCD 的对角线 BD 上一点,连接CP并延长,交AD于点 E,交 BA 的延长线于点 F.
(1)求证:
(2)如图②,连接 AC 交 BD 于 O,连接OE,若求证:
参考答案
1. D 【点拨】∵ 由题图可知, A.三角形各角的度数都是B.三角 形各角的度 数分别为 C.三角形各角的度数分别为 D.三角形各角的度数分别为 只D选项中三角形各角的度数与题干中三角形各角的度数相等.
2. C 【点拨】∵A.若添加 可用两角对应相等的两个三角形相似,证明△ABC∽ △ADE;B. 若添加∠C =∠AED,可用两角对应相等的两个三角形相似,证明△ABC∽△ADE;C.若添加AB·BC=AD·DE,不能证明△ABC∽△ADE;D.若添加AB·AE=AD·AC,可用两边对应成比例,且夹角相等的两个三角形相似,证明△ABC∽△ADE.
3.【证明】 ∴∠BAC=∠DAE, ∴∠EAD-∠EAB =∠BAC-∠EAB,∴∠BAD=∠CAE.
4. C 【点拨】∵∠A =∠B=90°,若△PAD与△PBC相似,可分两种情况:①若△APD∽△BPC,则 解得 AP =2.8. ②若△APD∽△BCP,则 解得AP=1 或6.∴满足条件的AP长为2.8 或1 或6,∴满足条件的点 P有3 个.
5. B 【点拨】∵在正方形ABCD 中,E是 BC 的中点,F是CD上一点,且∴②③正确.
6.2 条 【点拨】如图,①作 ②作 ∥因此共有 2 种作法.
【解】方法一:如图①,连接CF,AD. ∵ AF:BF =∥
方法二:如图②,过点 F 作. 交AC 于点 E,即 ∥
8.(1)【证明】∵ 四边形ABCD 是矩形,
(2)【解】 ∵四边形ABCD为矩形,
9.(1)【证明】∵∠1=∠BAC,∴∠1 +∠PAC=∠BAC+∠PAC,∴∠CAQ=∠BAP.∵ ∠2 =∠ABP,
(2) 【解】∠PQA = ∠ACB. 理由: ∵ AC ·AP =
∵∠1 =∠BAC,∴△APQ∽△ABC,∴∠PQA =∠ACB.
10.【证明】(1)∵ △ABC 绕点 A 逆时针旋转60°得到△ADE,∴△ABC≌△ADE.∴∠EAC=∠BAC,AC=AE.∵∠EAC=60°,∴△AEC 为等边三角形, ∠BAC=60°.∴∠ACE=60°=∠BAC,∴AB∥EC.
(2)∵△ABC≌△ADE,∴ ∠AED=∠ACB.又∵∠ADE=∠FDC,∴ △ADE∽△FDC.又∵∠ADF=∠EDC,∴△DAF∽△DEC.
11.【证明】(1)∵ 四边形 ABCD 是菱形,∴ AD= CD,∠CDP =∠ADP,CD∥AB.
在△CDP和△ADP中,
∴△CDP≌△ADP(SAS),∴PC=PA,∠DCP=∠DAP.
∵∥
∥.
∵四边形 ABCD 是菱形,
点方法 题(1) 中的相似三角形是常见的共边共角型, 一般用“两角相等的两个三角形相似”证明相似.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
