3.1.1圆柱的认识同步分层作业(含答案)2023-2024学年六年级数学下册同步分层作业设计(人教版)
文档属性
| 名称 | 3.1.1圆柱的认识同步分层作业(含答案)2023-2024学年六年级数学下册同步分层作业设计(人教版) |

|
|
| 格式 | docx | ||
| 文件大小 | 344.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-31 11:40:37 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
3.1.1圆柱的认识同步分层作业
知识回顾
⒈圆柱各部分名称及特征。
(1)拿一个圆柱形的实物,看看圆柱有哪几部分组成?自学课本18页。
我的发现:圆柱有两个 和一个 组成。
圆柱的两个圆面叫做 ;周围的面叫做 ;
两底面之间的距离叫做 。
(2)圆柱有什么特征?小组内说说自己的想法。
圆柱的特征:圆柱的两底面都是 ,并且大小 ;
圆柱的侧面是 ;有 条高,长度都相等。
⒉圆柱的侧面、底面及之间的关系。
圆柱的侧面展开后是什么形状?剪一剪再展开。
我的发现:沿圆柱的高剪开侧面,侧面是 ,长方形的长等于圆柱 的 周长,长方形的宽等于圆柱的 。
提升训练
一、填空题
1.圆柱的( )叫做底面,它们是( )的两个圆。
2.圆柱两个底面之间的距离叫做( ),圆柱有( )条高。
3.一个长方形长5厘米,宽4厘米,如果以宽为轴旋转一周得到一个立体图形,得到的是( )。
4.将一张长5cm,宽3cm的长方形硬纸板,以长为轴旋转一周得到的立体图形是( ),这个立体图形的一个底面的面积是( )。
5.一个圆柱体的侧面展开后,正好得到一个边长25.12厘米的正方形,圆柱体的高是( )厘米。
6.一个圆柱的侧面展开后刚好得到一个正方形,这个圆柱的底面半径是,这个圆柱的高是( )。
7.把一个边长为31.4cm的正方形卷成一个最大的圆柱,再给这个圆柱配一个底面,这个底面的面积是( )cm2。(接头处都忽略不计)
8.小明要做一个圆柱形的纸筒,用下图这张纸做圆柱的侧面(接头处忽略不计),要剪出半径是( )cm的圆,才能做成这个圆柱的两个底面。
长18.84cm 宽12.56cm
二、选择题
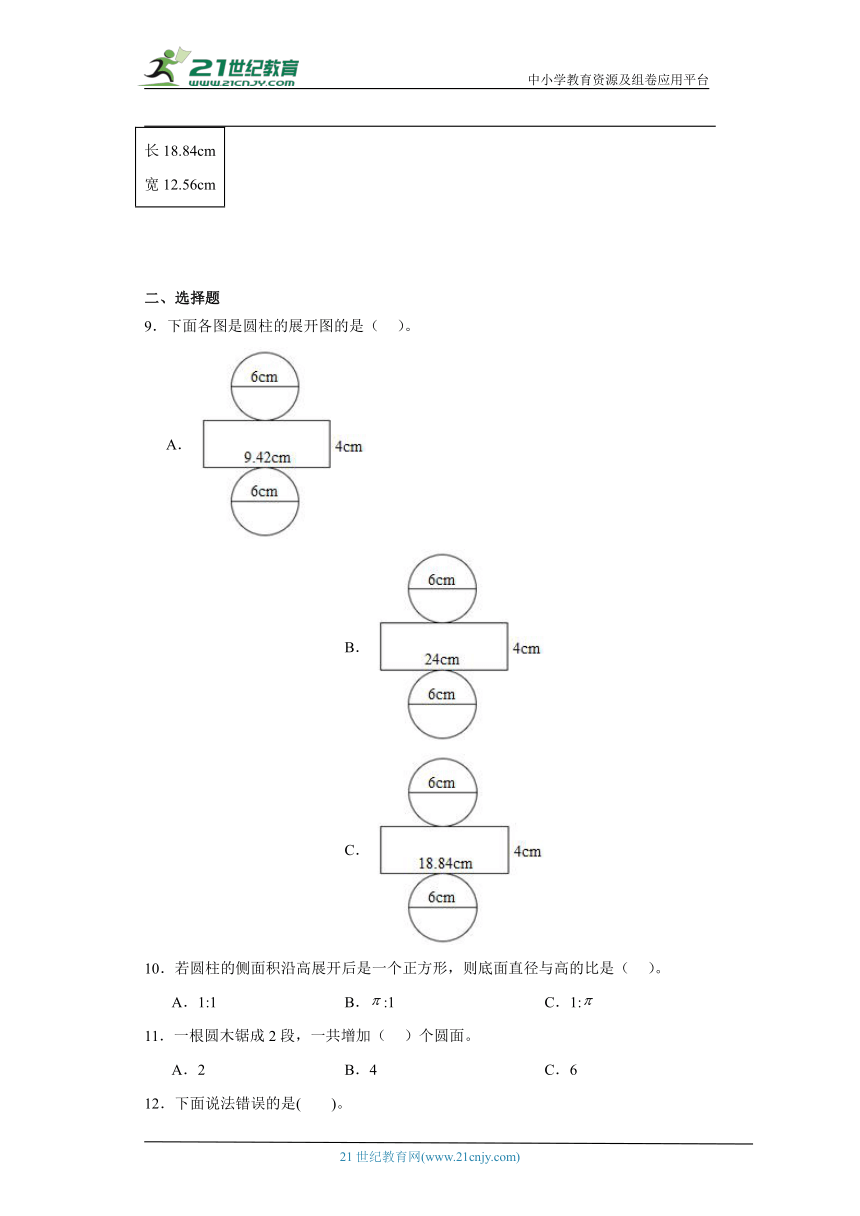
9.下面各图是圆柱的展开图的是( )。
A. B. C.
10.若圆柱的侧面积沿高展开后是一个正方形,则底面直径与高的比是( )。
A.1:1 B.:1 C.1:
11.一根圆木锯成2段,一共增加( )个圆面。
A.2 B.4 C.6
12.下面说法错误的是( )。
A.圆柱的两个底面之间的距离就是圆柱的高。
B.圆柱的两个底面是面积相等的两个圆。
C.把一个圆柱在平坦的桌面上滚动,滚动的路线是圆。
13.下面不能围成圆柱侧面的是( )。
A. B. C. D.
14.一个圆柱形蛋糕盒的底面直径是,高是,用彩绳将它捆扎(如图),打结处在上底面圆的圆心,打结部分的彩绳长。一共需要( )彩绳。
A.96 B.138 C.216 D.246
三、判断题
15.圆柱体的底面直径和高可以相等.( )
16.一个长方形以它的一条边为轴,旋转一周得到的旋转体是一个圆柱体。( )
17.电线杆的上、下两个面是圆形,所以电线杆就是圆柱。( )
18.两个底面是圆形的物体一定是圆柱形。( )
19.圆柱的侧面展开图可以是长方形、平行四边形或梯形。( )
四、解答题
20.下面的图形哪些是圆柱?在下面的( )里画“√”。
21.转动长方形ABCD,生成右面的两个圆柱。说一说它们分别是以长方形的哪条边为轴旋转而成的,底面半径和高分别是多少。
22.一个长方体盒子从里面量,长12厘米、宽8厘米、高2厘米,里面摆放底面半径为2厘米、高为1厘米的圆柱,最多可以放多少个?
23.一个圆柱的侧面展开是一个正方形.如果高增加2厘米,侧面积增加12.56平方厘米.原来这个圆柱的侧面积是多少平方厘米?
24.下面这个长方形的长是10厘米,宽是2厘米,分别以长和宽为轴旋转一周,能得到什么图形?它们的占地面积分别是多少呢?
25.看图计算.如图,一张长方形的纸,剪下图中的一个长方形,正好做成一个无盖的圆柱,请你求出这张长方形纸的面积.(单位:厘米)
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
参考答案:
1. 上、下两个面 大小一样
【解析】略
2. 高 无数
【详解】略
3.圆柱
【分析】如下图,以长方形的宽为轴旋转一周,会得到一个底面半径是5厘米,高是4厘米的圆柱。
【详解】如上图所示,一个长方形长5厘米,宽4厘米,如果以宽为轴旋转一周得到一个立体图形,得到的是圆柱。
【点睛】“点、线、面、体”之间的联系:点动成线,线动成面,面动成体。
4. 圆柱/圆柱体 28.26cm2/28.26平方厘米
【分析】以长方形的长为轴旋转一周得到一个圆柱体,长方形的长是圆柱的高,长方形的宽是圆柱的底面半径,根据圆的面积计算公式求出圆柱的底面积即可。
【详解】分析可知,将一张长5cm,宽3cm的长方形硬纸板,以长为轴旋转一周得到的立体图形是圆柱体,且长方形的宽为圆柱的底面半径。
底面积:3.14×32=28.26(cm2)
【点睛】掌握圆柱的特征并根据圆柱的底面半径求出底面积是解答题目的关键。
5.25.12
【分析】根据圆柱体的特征,侧面展开得到一个长方形,这个长方形的长等于圆柱体的底面周长,宽等于圆柱体的高。因为本题中圆柱侧面展开是正方形,而正方形的边长相等,可得此时圆柱的底面周长与高相等,所以圆柱的高是25.12厘米。
【详解】一个圆柱体的侧面展开后,正好得到一个边长25.12厘米的正方形,那么圆柱体的高也就是25.12厘米。
【点睛】此题主要考查圆柱体的特征,且能够充分想象其展开图的具体样子,进而结合题目数据解答。
6.12.56
【分析】圆柱底面周长等于高时,侧面沿高展开是正方形,求出这个圆柱的底面周长,就是圆柱的高。
【详解】3.14×2×2=12.56(分米)
故答案为:12.56
【点睛】本题考查了圆柱侧面展开图,明确圆柱的侧面展开图是正方形,即圆柱的底面周长和高相等是解决本题的关键。
7.78.5
【分析】把一个正方形卷成最大的圆柱,正方形的边长等于圆柱的底面周长,根据正方形的边长求出圆柱的底面半径,再利用“”求出圆柱的底面积。
【详解】半径:31.4÷3.14÷2
=10÷2
=5(cm)
底面积:3.14×52
=3.14×25
=78.5(cm2)
【点睛】掌握圆柱展开图的特征以及圆的周长和面积的计算公式是解答题目的关键。
8.3或2
【分析】圆柱的侧面展开后是一个长18.84cm,宽12.56cm的长方形,底面周长可能是18.84cm或12.56cm,根据圆的周长=2r,求出半径即可。
【详解】当底面周长是18.84cm时,半径为:
18.84÷3.14÷2
=6÷2
=3(厘米)
当底面周长是12.56cm时,半径为:
12.56÷3.14÷2
=4÷2
=2(厘米)
【点睛】本题考查圆柱的展开图、圆的周长,解答本题的关键是掌握圆柱的底面周长可能是侧面展开的长方形的长或宽。
9.C
【分析】根据圆柱展开图的特点,圆柱的底面周长等于长方形的长,据此判断即可。
【详解】A.3.14×6=18.84(cm),18.84≠9.42,所以不符合圆柱展开图的特点。
B.3.14×6=18.84(cm),18.84≠24,所以不符合圆柱展开图的特点。
C.3.14×6=18.84(cm),符合圆柱展开图的特点。
故答案为:C
【点睛】本题考查圆柱展开图的特点,明确圆柱的底面周长等于长方形的长是解题的关键。
10.C
【解析】略
11.A
【分析】一根圆木每锯一下就会新露出2个横截面,据此解答。
【详解】一根圆木锯成2段,一共增加2个圆面。
故选:A。
【点睛】新露出横截面的个数(段数-1)×2。
12.C
【详解】略
13.D
【分析】根据圆柱的侧面展开图的特点,将圆柱的侧面的几种展开方法与展开后的图形列举出来,利用排除法即可进行选择。
【详解】如果圆柱的底面周长与高相等,把圆柱的侧面展开有两种情况:①沿高线剪开:此时圆柱的侧面展开是一个长方形或者正方形;②不沿高线剪:斜着剪开将会得到一个平行四边形,如果裁剪的不规则,它们合在一起也会重合。
根据上述圆柱的展开图的特点可得:题干的四个图形中只有正六边形不能围成圆柱。
故答案为:D
【点睛】本题考查了圆柱的侧面展开图,同一个立体图形按不同的方式展开,得到的平面展开图是不一样的,熟记常见几何体的侧面展开图是解决本题的关键。
14.D
【分析】彩绳的长度=底面直径×4+高×4+打结部分长度,代入数据计算即可。
【详解】40×4+14×4+30
=160+56+30
=246(厘米)
一共需要246厘米彩绳。
故选择:D
【点睛】根据图示找出彩绳的长度包含哪几个部分是解题关键。
15.√
【详解】略
16.√
【详解】根据圆柱体的特征,圆柱体的上、下底面是完全相同的两个圆,侧面是一个曲面,侧面展开是一个长方形,一个长方形以一条边为轴,旋转一周得到的旋转体是一个圆柱体。
故答案为:√
【点睛】此题主要考查圆柱的特征。
17.×
【分析】圆柱每个横截面都是相等的,上下两个面是完全相同的圆,结合电线杆的特征进行分析。
【详解】虽然电线杆的上、下两个面是圆形,但是下端粗上端细,上下两个面的面积不相等,所以电线杆不是圆柱。
故答案为:×
【点睛】掌握圆柱的基本特征是解决本题的关键。
18.×
【分析】圆柱有3个面,上下底面是两个完全一样的圆形,侧面是一个曲面,侧面展开后是一个长方形(正方形),题干部分说的是底面是圆,但这两个圆是否完全一样是未知的,所以这个图形未必一定是圆柱。
【详解】两个底面是圆形的物体有可能是圆柱形,所以原题干说法错误。
故答案为:×
19.×
【分析】把一个圆柱沿高剪开,当圆柱的底面周长等于圆柱的高时,展开的图形是正方形;当圆柱的底面周长不等于圆柱的高时,展开的图形是长方形;当把一个圆柱不是沿高剪开,而是斜着剪开,得到的图形是平行四边形,由此做出判断。
【详解】根据分析:将圆柱的侧面展开有可能是长方形,也有可能是正方形,还有可能是平行四边形。但不可能是梯形。
故答案为:×
【点睛】此题主要考查了用不同的方法把圆柱的侧面展开时会得到不同的形状。
20.见详解
【分析】圆柱的是由3个面围成的。
圆柱的特征:
1.上下一样粗细;
2.圆柱的上下两个底面都是圆,并且大小一样;
3.有无数条高;
4.侧面展开是一个长方形或平行四边形或正方形。据此判断。
【详解】图一上下不一样粗细,且两个底面大小不同,不是圆柱;
图三、四上下粗细不同,不是圆柱;
图六两个底面大小不同,不是圆柱;
图二、五符合圆柱的特征。
【点睛】本题考查圆柱的认识,要熟练掌握圆柱的特征。
21.见详解
【分析】根据面动成体,一个长方形绕长(或宽)为旋转轴转动一周,将得到一个以长(或宽)为高,宽(或长)为底面半径的圆柱。
【详解】长方形ABCD以AB或CD边为轴旋转一周,生成圆柱(1),得到的圆柱底面半径为2厘米,高为1厘米;
长方形ABCD以AD或BC为轴旋转一周,生成圆柱(2),得到的圆柱底面半径为1厘米,高为2厘米。
22.12个
【分析】圆柱的底面半径是2厘米,直径就是4厘米,长方体的长是12厘米,所以长边可以放3个圆柱;宽是8厘米,所以可以放2行;长方体的高是2厘米,圆柱的高是1厘米,所以可以放2层。
【详解】2×2=4(厘米)
12÷4=3(个)
8÷4=2(行)
2÷1=2(层)
3×2×2
=6×2
=12(个)
答:最多可以放12个。
【点睛】重点是知道长方体中长边可以放几个,宽边可以放几个,高能放几个。
23.39.4384平方厘米
【分析】如果高增加2厘米,表面积增加12.56平方厘米,那么圆柱的底面周长应该是12.56÷2=6.28厘米,此长度应该是圆柱原来的底面周长,以及高,依据侧面积=底面周长×高即可解答.
【详解】(12.56÷2)×(12.56÷2),
=6.28×6.28,
=39.4384(平方厘米);
答:原来这个圆柱的侧面积是39.4384平方厘米.
24.圆柱,以长为轴旋转一周的占地面积是12.56平方厘米,以宽为轴旋转一周的占地面积是314平方厘米
【分析】由题意可知,以长为轴旋转一周,得到一个底面半径是2厘米,高是10厘米的圆柱体;以宽为轴旋转一周,得到一个底面半径是10厘米,高是2厘米的圆柱体;求它们的占地面积即求圆柱的底面积,根据圆的面积公式:S=πr2,据此解答即可。
【详解】3.14×22=12.56(平方厘米)
3.14×102=314(平方厘米)
答:分别以长和宽为轴旋转一周,能得到圆柱,以长为轴旋转一周的占地面积是12.56平方厘米,以宽为轴旋转一周的占地面积是314平方厘米。
【点睛】本题考查圆柱的特点,明确圆柱的特征是解题的关键。
25.414平方厘米
【详解】试题分析:根据圆的周长公式C=πd,求出剪下的圆的周长,即剪下的长方形的长,而圆的直径就是长方形的宽,由此根据长方形的面积公式S=ab,即可求出长方形纸的面积.
解:长方形纸的长是:3.14×10+10,
=31.4+10,
=41.4(厘米),
长方形纸的面积:41.4×10=414(平方厘米),
答:这张长方形纸的面积是414平方厘米.
点评:关键是根据题意知道剪下的圆与剪下的长方形之间的关系,再利用相应的公式与基本的数量关系解决问题.
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
中小学教育资源及组卷应用平台
3.1.1圆柱的认识同步分层作业
知识回顾
⒈圆柱各部分名称及特征。
(1)拿一个圆柱形的实物,看看圆柱有哪几部分组成?自学课本18页。
我的发现:圆柱有两个 和一个 组成。
圆柱的两个圆面叫做 ;周围的面叫做 ;
两底面之间的距离叫做 。
(2)圆柱有什么特征?小组内说说自己的想法。
圆柱的特征:圆柱的两底面都是 ,并且大小 ;
圆柱的侧面是 ;有 条高,长度都相等。
⒉圆柱的侧面、底面及之间的关系。
圆柱的侧面展开后是什么形状?剪一剪再展开。
我的发现:沿圆柱的高剪开侧面,侧面是 ,长方形的长等于圆柱 的 周长,长方形的宽等于圆柱的 。
提升训练
一、填空题
1.圆柱的( )叫做底面,它们是( )的两个圆。
2.圆柱两个底面之间的距离叫做( ),圆柱有( )条高。
3.一个长方形长5厘米,宽4厘米,如果以宽为轴旋转一周得到一个立体图形,得到的是( )。
4.将一张长5cm,宽3cm的长方形硬纸板,以长为轴旋转一周得到的立体图形是( ),这个立体图形的一个底面的面积是( )。
5.一个圆柱体的侧面展开后,正好得到一个边长25.12厘米的正方形,圆柱体的高是( )厘米。
6.一个圆柱的侧面展开后刚好得到一个正方形,这个圆柱的底面半径是,这个圆柱的高是( )。
7.把一个边长为31.4cm的正方形卷成一个最大的圆柱,再给这个圆柱配一个底面,这个底面的面积是( )cm2。(接头处都忽略不计)
8.小明要做一个圆柱形的纸筒,用下图这张纸做圆柱的侧面(接头处忽略不计),要剪出半径是( )cm的圆,才能做成这个圆柱的两个底面。
长18.84cm 宽12.56cm
二、选择题
9.下面各图是圆柱的展开图的是( )。
A. B. C.
10.若圆柱的侧面积沿高展开后是一个正方形,则底面直径与高的比是( )。
A.1:1 B.:1 C.1:
11.一根圆木锯成2段,一共增加( )个圆面。
A.2 B.4 C.6
12.下面说法错误的是( )。
A.圆柱的两个底面之间的距离就是圆柱的高。
B.圆柱的两个底面是面积相等的两个圆。
C.把一个圆柱在平坦的桌面上滚动,滚动的路线是圆。
13.下面不能围成圆柱侧面的是( )。
A. B. C. D.
14.一个圆柱形蛋糕盒的底面直径是,高是,用彩绳将它捆扎(如图),打结处在上底面圆的圆心,打结部分的彩绳长。一共需要( )彩绳。
A.96 B.138 C.216 D.246
三、判断题
15.圆柱体的底面直径和高可以相等.( )
16.一个长方形以它的一条边为轴,旋转一周得到的旋转体是一个圆柱体。( )
17.电线杆的上、下两个面是圆形,所以电线杆就是圆柱。( )
18.两个底面是圆形的物体一定是圆柱形。( )
19.圆柱的侧面展开图可以是长方形、平行四边形或梯形。( )
四、解答题
20.下面的图形哪些是圆柱?在下面的( )里画“√”。
21.转动长方形ABCD,生成右面的两个圆柱。说一说它们分别是以长方形的哪条边为轴旋转而成的,底面半径和高分别是多少。
22.一个长方体盒子从里面量,长12厘米、宽8厘米、高2厘米,里面摆放底面半径为2厘米、高为1厘米的圆柱,最多可以放多少个?
23.一个圆柱的侧面展开是一个正方形.如果高增加2厘米,侧面积增加12.56平方厘米.原来这个圆柱的侧面积是多少平方厘米?
24.下面这个长方形的长是10厘米,宽是2厘米,分别以长和宽为轴旋转一周,能得到什么图形?它们的占地面积分别是多少呢?
25.看图计算.如图,一张长方形的纸,剪下图中的一个长方形,正好做成一个无盖的圆柱,请你求出这张长方形纸的面积.(单位:厘米)
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
参考答案:
1. 上、下两个面 大小一样
【解析】略
2. 高 无数
【详解】略
3.圆柱
【分析】如下图,以长方形的宽为轴旋转一周,会得到一个底面半径是5厘米,高是4厘米的圆柱。
【详解】如上图所示,一个长方形长5厘米,宽4厘米,如果以宽为轴旋转一周得到一个立体图形,得到的是圆柱。
【点睛】“点、线、面、体”之间的联系:点动成线,线动成面,面动成体。
4. 圆柱/圆柱体 28.26cm2/28.26平方厘米
【分析】以长方形的长为轴旋转一周得到一个圆柱体,长方形的长是圆柱的高,长方形的宽是圆柱的底面半径,根据圆的面积计算公式求出圆柱的底面积即可。
【详解】分析可知,将一张长5cm,宽3cm的长方形硬纸板,以长为轴旋转一周得到的立体图形是圆柱体,且长方形的宽为圆柱的底面半径。
底面积:3.14×32=28.26(cm2)
【点睛】掌握圆柱的特征并根据圆柱的底面半径求出底面积是解答题目的关键。
5.25.12
【分析】根据圆柱体的特征,侧面展开得到一个长方形,这个长方形的长等于圆柱体的底面周长,宽等于圆柱体的高。因为本题中圆柱侧面展开是正方形,而正方形的边长相等,可得此时圆柱的底面周长与高相等,所以圆柱的高是25.12厘米。
【详解】一个圆柱体的侧面展开后,正好得到一个边长25.12厘米的正方形,那么圆柱体的高也就是25.12厘米。
【点睛】此题主要考查圆柱体的特征,且能够充分想象其展开图的具体样子,进而结合题目数据解答。
6.12.56
【分析】圆柱底面周长等于高时,侧面沿高展开是正方形,求出这个圆柱的底面周长,就是圆柱的高。
【详解】3.14×2×2=12.56(分米)
故答案为:12.56
【点睛】本题考查了圆柱侧面展开图,明确圆柱的侧面展开图是正方形,即圆柱的底面周长和高相等是解决本题的关键。
7.78.5
【分析】把一个正方形卷成最大的圆柱,正方形的边长等于圆柱的底面周长,根据正方形的边长求出圆柱的底面半径,再利用“”求出圆柱的底面积。
【详解】半径:31.4÷3.14÷2
=10÷2
=5(cm)
底面积:3.14×52
=3.14×25
=78.5(cm2)
【点睛】掌握圆柱展开图的特征以及圆的周长和面积的计算公式是解答题目的关键。
8.3或2
【分析】圆柱的侧面展开后是一个长18.84cm,宽12.56cm的长方形,底面周长可能是18.84cm或12.56cm,根据圆的周长=2r,求出半径即可。
【详解】当底面周长是18.84cm时,半径为:
18.84÷3.14÷2
=6÷2
=3(厘米)
当底面周长是12.56cm时,半径为:
12.56÷3.14÷2
=4÷2
=2(厘米)
【点睛】本题考查圆柱的展开图、圆的周长,解答本题的关键是掌握圆柱的底面周长可能是侧面展开的长方形的长或宽。
9.C
【分析】根据圆柱展开图的特点,圆柱的底面周长等于长方形的长,据此判断即可。
【详解】A.3.14×6=18.84(cm),18.84≠9.42,所以不符合圆柱展开图的特点。
B.3.14×6=18.84(cm),18.84≠24,所以不符合圆柱展开图的特点。
C.3.14×6=18.84(cm),符合圆柱展开图的特点。
故答案为:C
【点睛】本题考查圆柱展开图的特点,明确圆柱的底面周长等于长方形的长是解题的关键。
10.C
【解析】略
11.A
【分析】一根圆木每锯一下就会新露出2个横截面,据此解答。
【详解】一根圆木锯成2段,一共增加2个圆面。
故选:A。
【点睛】新露出横截面的个数(段数-1)×2。
12.C
【详解】略
13.D
【分析】根据圆柱的侧面展开图的特点,将圆柱的侧面的几种展开方法与展开后的图形列举出来,利用排除法即可进行选择。
【详解】如果圆柱的底面周长与高相等,把圆柱的侧面展开有两种情况:①沿高线剪开:此时圆柱的侧面展开是一个长方形或者正方形;②不沿高线剪:斜着剪开将会得到一个平行四边形,如果裁剪的不规则,它们合在一起也会重合。
根据上述圆柱的展开图的特点可得:题干的四个图形中只有正六边形不能围成圆柱。
故答案为:D
【点睛】本题考查了圆柱的侧面展开图,同一个立体图形按不同的方式展开,得到的平面展开图是不一样的,熟记常见几何体的侧面展开图是解决本题的关键。
14.D
【分析】彩绳的长度=底面直径×4+高×4+打结部分长度,代入数据计算即可。
【详解】40×4+14×4+30
=160+56+30
=246(厘米)
一共需要246厘米彩绳。
故选择:D
【点睛】根据图示找出彩绳的长度包含哪几个部分是解题关键。
15.√
【详解】略
16.√
【详解】根据圆柱体的特征,圆柱体的上、下底面是完全相同的两个圆,侧面是一个曲面,侧面展开是一个长方形,一个长方形以一条边为轴,旋转一周得到的旋转体是一个圆柱体。
故答案为:√
【点睛】此题主要考查圆柱的特征。
17.×
【分析】圆柱每个横截面都是相等的,上下两个面是完全相同的圆,结合电线杆的特征进行分析。
【详解】虽然电线杆的上、下两个面是圆形,但是下端粗上端细,上下两个面的面积不相等,所以电线杆不是圆柱。
故答案为:×
【点睛】掌握圆柱的基本特征是解决本题的关键。
18.×
【分析】圆柱有3个面,上下底面是两个完全一样的圆形,侧面是一个曲面,侧面展开后是一个长方形(正方形),题干部分说的是底面是圆,但这两个圆是否完全一样是未知的,所以这个图形未必一定是圆柱。
【详解】两个底面是圆形的物体有可能是圆柱形,所以原题干说法错误。
故答案为:×
19.×
【分析】把一个圆柱沿高剪开,当圆柱的底面周长等于圆柱的高时,展开的图形是正方形;当圆柱的底面周长不等于圆柱的高时,展开的图形是长方形;当把一个圆柱不是沿高剪开,而是斜着剪开,得到的图形是平行四边形,由此做出判断。
【详解】根据分析:将圆柱的侧面展开有可能是长方形,也有可能是正方形,还有可能是平行四边形。但不可能是梯形。
故答案为:×
【点睛】此题主要考查了用不同的方法把圆柱的侧面展开时会得到不同的形状。
20.见详解
【分析】圆柱的是由3个面围成的。
圆柱的特征:
1.上下一样粗细;
2.圆柱的上下两个底面都是圆,并且大小一样;
3.有无数条高;
4.侧面展开是一个长方形或平行四边形或正方形。据此判断。
【详解】图一上下不一样粗细,且两个底面大小不同,不是圆柱;
图三、四上下粗细不同,不是圆柱;
图六两个底面大小不同,不是圆柱;
图二、五符合圆柱的特征。
【点睛】本题考查圆柱的认识,要熟练掌握圆柱的特征。
21.见详解
【分析】根据面动成体,一个长方形绕长(或宽)为旋转轴转动一周,将得到一个以长(或宽)为高,宽(或长)为底面半径的圆柱。
【详解】长方形ABCD以AB或CD边为轴旋转一周,生成圆柱(1),得到的圆柱底面半径为2厘米,高为1厘米;
长方形ABCD以AD或BC为轴旋转一周,生成圆柱(2),得到的圆柱底面半径为1厘米,高为2厘米。
22.12个
【分析】圆柱的底面半径是2厘米,直径就是4厘米,长方体的长是12厘米,所以长边可以放3个圆柱;宽是8厘米,所以可以放2行;长方体的高是2厘米,圆柱的高是1厘米,所以可以放2层。
【详解】2×2=4(厘米)
12÷4=3(个)
8÷4=2(行)
2÷1=2(层)
3×2×2
=6×2
=12(个)
答:最多可以放12个。
【点睛】重点是知道长方体中长边可以放几个,宽边可以放几个,高能放几个。
23.39.4384平方厘米
【分析】如果高增加2厘米,表面积增加12.56平方厘米,那么圆柱的底面周长应该是12.56÷2=6.28厘米,此长度应该是圆柱原来的底面周长,以及高,依据侧面积=底面周长×高即可解答.
【详解】(12.56÷2)×(12.56÷2),
=6.28×6.28,
=39.4384(平方厘米);
答:原来这个圆柱的侧面积是39.4384平方厘米.
24.圆柱,以长为轴旋转一周的占地面积是12.56平方厘米,以宽为轴旋转一周的占地面积是314平方厘米
【分析】由题意可知,以长为轴旋转一周,得到一个底面半径是2厘米,高是10厘米的圆柱体;以宽为轴旋转一周,得到一个底面半径是10厘米,高是2厘米的圆柱体;求它们的占地面积即求圆柱的底面积,根据圆的面积公式:S=πr2,据此解答即可。
【详解】3.14×22=12.56(平方厘米)
3.14×102=314(平方厘米)
答:分别以长和宽为轴旋转一周,能得到圆柱,以长为轴旋转一周的占地面积是12.56平方厘米,以宽为轴旋转一周的占地面积是314平方厘米。
【点睛】本题考查圆柱的特点,明确圆柱的特征是解题的关键。
25.414平方厘米
【详解】试题分析:根据圆的周长公式C=πd,求出剪下的圆的周长,即剪下的长方形的长,而圆的直径就是长方形的宽,由此根据长方形的面积公式S=ab,即可求出长方形纸的面积.
解:长方形纸的长是:3.14×10+10,
=31.4+10,
=41.4(厘米),
长方形纸的面积:41.4×10=414(平方厘米),
答:这张长方形纸的面积是414平方厘米.
点评:关键是根据题意知道剪下的圆与剪下的长方形之间的关系,再利用相应的公式与基本的数量关系解决问题.
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
