4.2.1正比例同步分层作业(含答案)2023-2024学年六年级数学下册同步分层作业设计(人教版)
文档属性
| 名称 | 4.2.1正比例同步分层作业(含答案)2023-2024学年六年级数学下册同步分层作业设计(人教版) |

|
|
| 格式 | docx | ||
| 文件大小 | 321.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-31 12:00:37 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
4.2.1 正比例同步分层作业
一、填空题
1.已知:A×=B×,A与B成 比例,A∶B= ∶ 。
2.小明买4支钢笔用了16元,照这样计算这句话中的“照这样计算”意思是钢笔的( )是一定的,( )和( )成( )比例关系。
3.高一定,圆柱的体积与( )成正比例;三角形的面积一定,它的底与高成( )比例。
4.如果7x=9y,则x∶y=( )∶( ),x和y成( )比例。
5.在没有余数的除法里,除数一定,被除数和商成( )比例。
6.如果(A,B都不为零),则A( )B(填>,<,=);A和B成( )比例。
7.明明打字的时间和打字的总字数如下表。
时间/分 5 7 16 20 34 40 50
总字数/个 300 420 960 1200 2040 2400 3000
在上表中,相关联的量是( )和( ),( )随着( )的变化而变化,( )是一定的。因此,总字数和时间成( )。
二、选择题
8.表示x和y成正比例的式子是( )
A.x=7y B.x+y=7 C.x=
9.下列式子中,x与y成正比例的是( )
A.y=x+8 B.=x C.x=y
10.下面表示a和b成正比例的式子是( )。(a、b均不为0)
A.a=b+3 B.a=5b C.b=a-4
11.下面各组量成正比例的是( )。
A.正方形的面积和边长 B.儿童年龄一定,身高和体重
C.一个播音员播音的速度一定,播音的字数和时间
12.买同样的书,花的总钱数与( )成正比例。
A.书的本数 B.书的页数 C.书的单价
13.王小亮在弹簧秤上挂了3千克的物体,弹簧伸长约1.5厘米,在这个弹簧秤上挂2.5千克物体时,弹簧大约伸长( )厘米。
A.1.25 B.1.5 C.1
14.下列说法正确的是( )。
A.三角形面积一定时,它的底与高成正比例
B.三角形的底一定时,它的面积与高成正比例
C.三角形的高一定时,它的面积与底不成正比例
三、判断题
15.乐乐和爸爸的年龄差不变,他们的年龄成正比例.( )
16.梯形的上底和下底的和不变,梯形的面积和高成正比例关系。( )
17.物体的高度和影长成正比例。( )
18.如果“x+y=125”,那么,x和y就成正比例关系。( )
19.小麦的出粉率一定,小麦的总重量和面粉的重量成正比例关系。( )
四、解答题
20.下表中x和y两个量成正比例,请把表格填完整。
x 15 120 12
y 25 5 10
21.看图回答问题。
(1)苹果的总价和购买的数量成( )比例。
(2)从图像上看,贵一些的水果是( )。
(3)买2千克香蕉需要( )元,买5千克苹果需要( )元。
22.一本课外书有275页,亮亮前3天看了75页,照这样的速度,他看完这本课外书需要多少天?(用比例解答)
23.活动课上,数学老师带领小朋友们测量校园里一棵古树的高度。他们先量出古树影子的长度是10.8米,同时在古树附近竖立一根3米长的标杆,量得它的影子长度是1.8米。请问这棵古树高几米?
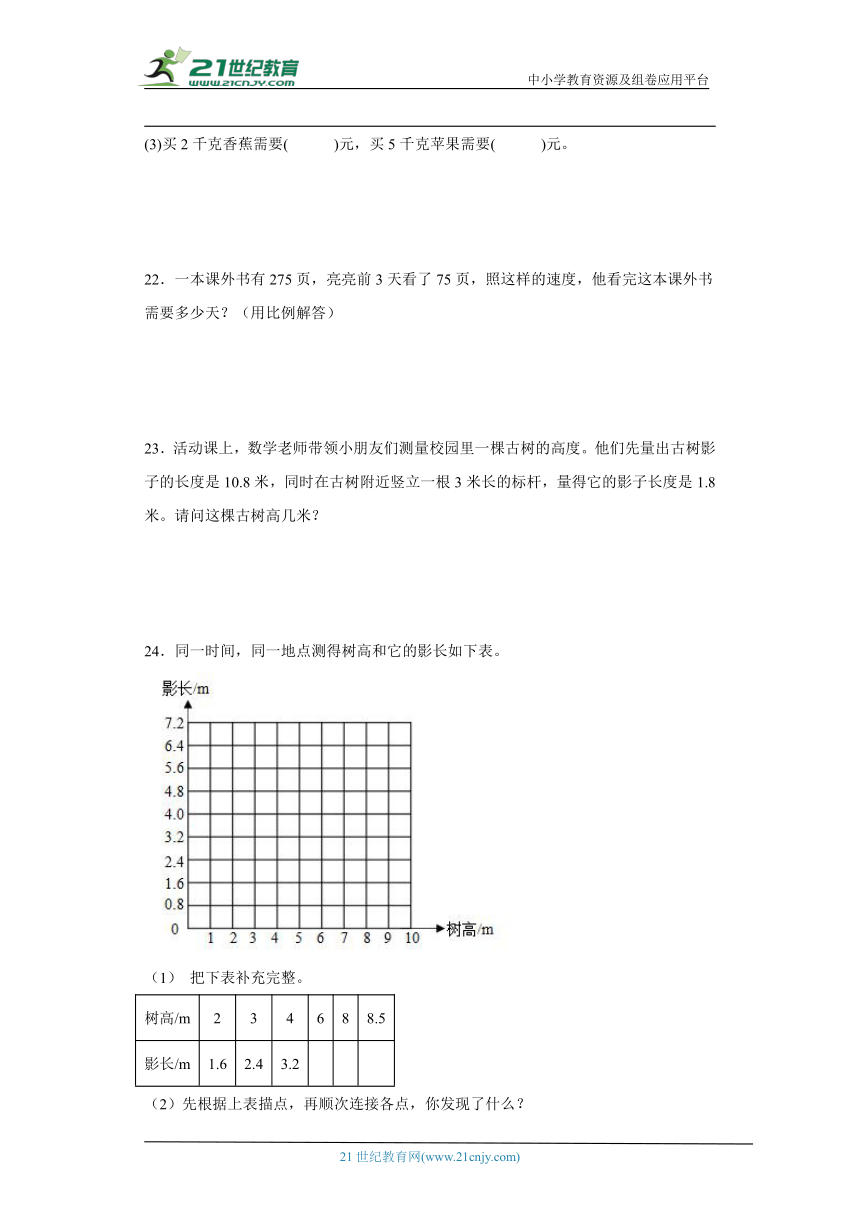
24.同一时间,同一地点测得树高和它的影长如下表。
(1) 把下表补充完整。
树高/m 2 3 4 6 8 8.5
影长/m 1.6 2.4 3.2
(2)先根据上表描点,再顺次连接各点,你发现了什么?
(3)树高和影长成( )比例。
(4)点(12,9.6),( )这条直线上。(填“在”或“不在”)。
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
参考答案:
1. 正 4 9
【分析】(1)要判定A与B成什么比例关系,必须根据式子,进行推导,然后根据正、反比例的意义,分析数量关系,找出一定的量,然后看那两个变量是比值一定还是乘积一定,从而判定成什么比例关系;
(2)逆用比例的基本性质,把等式A×=B×改写成一个外项是A,一个内项是B的比例,则和A相乘的数就作为比例的另一个外项,和B相乘的数就作为比例的另一个内项。
【详解】(1)因为A×=B×,所以A:B=∶=(一定),是A和B对应的比值一定,
符合正比例的意义,所以A和B成正比例;
(2)如果A×=B×,那么A:B=∶=4∶9
【点睛】此题考查根据正、反比例的意义辨识两种相关联的量成正比例还是反比例关系;也考查了比例性质的逆运用。
2. 单价 数量 总价 正
【分析】判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例;据此解答。
【详解】由分析可得:照这样计算这句话中的“照这样计算”意思是钢笔的单价是一定的,数量和总价成正比例关系。
【点睛】此题属于辨识成正、反比例的量,就看这两个量是对应的比值一定,还是对应的乘积一定,再做判断。
3. 底面积 反
【分析】正比例关系式:(一定),两个相关联的量和的比值一定,那么和成正比例;反比例关系式:(一定),两个相关联的量和的乘积一定,那么和成反比例。据此解答。
【详解】①由圆柱的体积,可得:圆柱的高,高一定,即比值一定,则圆柱的体积与底面积成正比例。
②三角形的面积=底×高÷2,面积一定,即乘积一定,则三角形的底与高成反比例。
【点睛】掌握正、反比例的意义是解题的关键。
4. 9 7 正
【分析】根据比例的基本性质,先将等积式改写成比例式,再根据正、反比例的意义判定比例关系。
【详解】如果7x=9y
则x∶y=9∶7
x∶y
=9∶7
=
x∶y的比值一定,所以x和y成正比例关系。
【点睛】本题考查了比例的基本性质以及正、反比例的意义,两个相关联的量,若其比值一定,这两个量成正比例关系;若其乘积一定,这两个量成反比例关系。
5.正
【分析】两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的比值一定,这两种量就叫作成正比例的量,它们的关系叫作正比例关系,据此解答。
【详解】由“被除数÷除数=商”可知,被除数÷商=除数(一定),在没有余数的除法里,除数一定,被除数和商成正比例。
【点睛】本题主要考查正比例关系的辨识,掌握正比例关系的意义是解答题目的关键。
6. < 正
【分析】积一定,一个数乘的数越小其本身越大;x÷y=k(一定),x和y成正比例关系,据此分析。
【详解】如果(A,B都不为零),>,则A<B;,两边同时÷B÷,可得,A和B成正比例。
【点睛】关键是掌握分数乘法的计算方法,理解正比例的意义,商一定是正比例关系。
7. 总字数 时间 总字数 时间 比值 正比例
【分析】由表中数据可知,打字的总字数随着打字时间的变化而变化,经计算分析可知总字数与打字时间的比值是一个定值(60),据此可解答。
【详解】===…==60(比值一定)
在上表中,相关联的量是总字数和时间,总字数随着时间的变化而变化,比值是一定的。因此,总字数和时间成正比例。
故答案为:总字数,时间,总字数,时间,比值,正比例。
【点睛】本题考查了正比例的意义,关键是要掌握的正比例的意义:两个相关联变化的量,如果这两个量对应的数的比值一定,这两个量成正比例。
8.A
【详解】略
9.C
【详解】x=y
=
故答案为:C
10.B
【分析】
正比例:两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的比值一定(也就是商一定),这两种量成正比例关系。
【详解】A.a=b+3,则a-b=3(一定),差一定,a和b不成正比例;
B.a=5b,则a÷b=5(一定),商一定,a和b成正比例;
C.b=a-4,则a-b=4(一定),差一定,a和b不成正比例。
故答案为:B
11.C
【分析】
两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的比值一定,这两种量就叫做成正比例的量,它们的关系叫做正比例关系,据此解答。
【详解】A.正方形的面积=边长×边长,边长=面积÷边长,边长不一定,比值不一定,因此不符合题意;
B.儿童的身高和体重不相关,不符合题意;
C.播音的字数÷时间=播音的速度,一个播音员播音的速度一定,比值一定,符合题意。
因此一个播音员播音的速度一定,播音的字数和时间成正比例关系。
故答案为:C
12.A
【分析】依据正、反比例的意义,即若两个相关联的量的比值一定,则这两个量成正比例关系;若两个相关联的量的乘积一定,则这两个量成反比例关系,由此判断即可选择。
【详解】因为花的总钱数÷书的本数=书的价格(一定),是比值一定,所以花的总钱数与书的本数成正比例。
故答案为:A
13.A
【分析】因为在一定限度内,弹簧秤弹簧所挂物体的重量越大,伸长量也就越大,即弹簧的伸长与所挂物体的重量成正比例关系;又已知当挂上了3千克的物体,伸长约为1.5厘米,要求得挂上2.5千克的物体,伸长大约多少,设此时弹簧大约伸长x厘米,可列比例式:3∶1.5=2.5∶x,解这个比例即可。
【详解】解:设弹簧大约伸长x厘米。
3∶1.5=2.5∶x
3x=1.5×2.5
3x=3.75
x=3.75÷3
x=1.25
在这个弹簧秤上挂2.5千克的物体时,弹簧大约伸长1.25厘米。
故答案为:A
【点睛】需要理解弹簧秤的工作原理,能利用正比例关系列式,解决生活中的问题。
14.B
【解析】略
15.×
【详解】略
16.√
【分析】判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定,如果是比值一定,就成正比例,如果是乘积一定,则成反比例。
【详解】梯形的面积÷高=(上底+下底)÷2(一定),商一定,所以梯形的面积和高成正比例关系。所以原题说法正确。
故答案为:√
【点睛】此题属于辨识成正、反比例的量,就看这两个量是对应的比值一定,还是对应的乘积一定,再作判断。
17.×
【分析】依据在同时同地,物体的高度与它的影长的比值是一定的,所以此时可知物体的高度和影长是正比例关系,由于题干没说同时同地,据此即可判断。
【详解】由于在同时同地时物体的高度和影长成正比例,原说法错误。
故答案为:×
【点睛】此题属于辨识成正、反比例的量,就看这两个量是对应的比值一定,还是对应的乘积一定,再作判断。
18.×
【分析】根据x÷y=k(一定),x和y成正比例关系,进行分析。
【详解】如果“x+y=125”, x和y是加法关系,不成比例关系。
故答案为:×
【点睛】关键是理解正比例的意义,商一定是正比例关系。
19.√
【分析】两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的比值一定(也就是商一定),这两种量成正比例关系。
【详解】小麦的出粉率=×100%
小麦的出粉率一定,即比值一定,则小麦的总重量和面粉的重量成正比例关系。
故答案为:√
20. 3 6 200 20
【分析】两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的比值一定,这两种量就叫做成正比例的量,它们的关系叫做正比例关系,用字母表示为(一定)。先根据表中x和y两个量成正比例,当x=15时,y=25,求出y与x的比值;再用x×比值求出y,或用y÷比值求出x。
【详解】
当y=5时,x=5÷=5×=3。
当y=10时,x=10÷=10×=6。
当x=120时,y=120×=200。
当x=12时,y=12×=20。
如下表:
x 15 3 120 6 12
y 25 5 200 10 20
【点睛】明确正比例的意义是解决此题的关键。
21.(1)正
(2)香蕉
(3) 16 20
【分析】(1)总价=单价×数量,单价=总价÷数量,单价一定,总价和数量成正比例。
(2)求单价,单价=总价÷数量,代入计算后,比较大小即可。
(3)总价=单价×数量,代入即可。
【详解】(1)从图中获得信息,单价一定,苹果的总价和购买的数量成正比例。
(2)8÷1=8(元)
4÷1=4(元)
8>4,所以香蕉比苹果贵一些。
(3)8×2=16(元)
4×5=20(元)
所以苹果的总价和购买的数量成正比例,从图像上看,贵一些的水果是香蕉,买2千克香蕉需要16元,买5千克苹果需要20元。
【点睛】此题考查了正比例的量的应用知识,解答本题的关键是掌握正比例的概念。
22.11天
【分析】根据“照这样的速度”可知,看的页数∶看的天数=每天看的页数(一定),比值一定,则看的页数和看的天数成正比例关系,据此列出正比例方程,并求解。
【详解】解:设他看完这本课外书需要天。
275∶=75∶3
75=275×3
75=825
=825÷75
=11
答:他看完这本课外书需要11天。
【点睛】关键是判断题目中的两种相关联的量成什么比例关系,据此列出相应的比例方程。
23.18米
【分析】根据题意可知,同一时间,同一地点测得物体高度与影子长度的比值一定,那么物体高度与影子长度成正比例关系,即古树的高度∶古树的影长=标杆的长度∶标杆的影长,据此列出正比例方程,并求解。
【详解】解:设这棵古树高米。
∶10.8=3∶1.8
1.8=10.8×3
1.8=32.4
1.8÷1.8=32.4÷1.8
=18
答:这棵古树高18米。
【点睛】关键是判断题目中的两种相关联的量成什么比例关系,据此列出相应的比例方程。
24.(1)
树高/m 2 3 4 6 8 8.5
影长/m 1.6 2.4 3.2 4.8 6.4 6.8
(2)图见详解
发现:所描点在一条直线上;
(3)正;
(4)在
【分析】(1)求出影长与树高的比值,进而求出树高为8米和8.5米的影长;
(2)所描点在一条直线上;
(3)根据图像可以看出树高与影长成正比例;
(4)求出9.6与12的比值与1.6与2的的比值比较得结论。
【详解】(1)1.6÷2=0.8,2.4÷3=0.8,3.2÷4=0.8,
所以,8×0.8=6.4(米),8.5×0.8=6.8(米)
(2)如下图:
发现:所描点在一条直线上。
(3)因为影长与树高的比值是一定的,所以树高与影长成正比例;
(4)9.6∶12=0.8,1.6÷2=0.8
因为0.8=0.8,所以点(12,9.6),在这条直线上。
【点睛】此题考查的是正比例的判断和图像,解答此题关键是掌握正比例的意义。
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
中小学教育资源及组卷应用平台
4.2.1 正比例同步分层作业
一、填空题
1.已知:A×=B×,A与B成 比例,A∶B= ∶ 。
2.小明买4支钢笔用了16元,照这样计算这句话中的“照这样计算”意思是钢笔的( )是一定的,( )和( )成( )比例关系。
3.高一定,圆柱的体积与( )成正比例;三角形的面积一定,它的底与高成( )比例。
4.如果7x=9y,则x∶y=( )∶( ),x和y成( )比例。
5.在没有余数的除法里,除数一定,被除数和商成( )比例。
6.如果(A,B都不为零),则A( )B(填>,<,=);A和B成( )比例。
7.明明打字的时间和打字的总字数如下表。
时间/分 5 7 16 20 34 40 50
总字数/个 300 420 960 1200 2040 2400 3000
在上表中,相关联的量是( )和( ),( )随着( )的变化而变化,( )是一定的。因此,总字数和时间成( )。
二、选择题
8.表示x和y成正比例的式子是( )
A.x=7y B.x+y=7 C.x=
9.下列式子中,x与y成正比例的是( )
A.y=x+8 B.=x C.x=y
10.下面表示a和b成正比例的式子是( )。(a、b均不为0)
A.a=b+3 B.a=5b C.b=a-4
11.下面各组量成正比例的是( )。
A.正方形的面积和边长 B.儿童年龄一定,身高和体重
C.一个播音员播音的速度一定,播音的字数和时间
12.买同样的书,花的总钱数与( )成正比例。
A.书的本数 B.书的页数 C.书的单价
13.王小亮在弹簧秤上挂了3千克的物体,弹簧伸长约1.5厘米,在这个弹簧秤上挂2.5千克物体时,弹簧大约伸长( )厘米。
A.1.25 B.1.5 C.1
14.下列说法正确的是( )。
A.三角形面积一定时,它的底与高成正比例
B.三角形的底一定时,它的面积与高成正比例
C.三角形的高一定时,它的面积与底不成正比例
三、判断题
15.乐乐和爸爸的年龄差不变,他们的年龄成正比例.( )
16.梯形的上底和下底的和不变,梯形的面积和高成正比例关系。( )
17.物体的高度和影长成正比例。( )
18.如果“x+y=125”,那么,x和y就成正比例关系。( )
19.小麦的出粉率一定,小麦的总重量和面粉的重量成正比例关系。( )
四、解答题
20.下表中x和y两个量成正比例,请把表格填完整。
x 15 120 12
y 25 5 10
21.看图回答问题。
(1)苹果的总价和购买的数量成( )比例。
(2)从图像上看,贵一些的水果是( )。
(3)买2千克香蕉需要( )元,买5千克苹果需要( )元。
22.一本课外书有275页,亮亮前3天看了75页,照这样的速度,他看完这本课外书需要多少天?(用比例解答)
23.活动课上,数学老师带领小朋友们测量校园里一棵古树的高度。他们先量出古树影子的长度是10.8米,同时在古树附近竖立一根3米长的标杆,量得它的影子长度是1.8米。请问这棵古树高几米?
24.同一时间,同一地点测得树高和它的影长如下表。
(1) 把下表补充完整。
树高/m 2 3 4 6 8 8.5
影长/m 1.6 2.4 3.2
(2)先根据上表描点,再顺次连接各点,你发现了什么?
(3)树高和影长成( )比例。
(4)点(12,9.6),( )这条直线上。(填“在”或“不在”)。
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
参考答案:
1. 正 4 9
【分析】(1)要判定A与B成什么比例关系,必须根据式子,进行推导,然后根据正、反比例的意义,分析数量关系,找出一定的量,然后看那两个变量是比值一定还是乘积一定,从而判定成什么比例关系;
(2)逆用比例的基本性质,把等式A×=B×改写成一个外项是A,一个内项是B的比例,则和A相乘的数就作为比例的另一个外项,和B相乘的数就作为比例的另一个内项。
【详解】(1)因为A×=B×,所以A:B=∶=(一定),是A和B对应的比值一定,
符合正比例的意义,所以A和B成正比例;
(2)如果A×=B×,那么A:B=∶=4∶9
【点睛】此题考查根据正、反比例的意义辨识两种相关联的量成正比例还是反比例关系;也考查了比例性质的逆运用。
2. 单价 数量 总价 正
【分析】判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例;据此解答。
【详解】由分析可得:照这样计算这句话中的“照这样计算”意思是钢笔的单价是一定的,数量和总价成正比例关系。
【点睛】此题属于辨识成正、反比例的量,就看这两个量是对应的比值一定,还是对应的乘积一定,再做判断。
3. 底面积 反
【分析】正比例关系式:(一定),两个相关联的量和的比值一定,那么和成正比例;反比例关系式:(一定),两个相关联的量和的乘积一定,那么和成反比例。据此解答。
【详解】①由圆柱的体积,可得:圆柱的高,高一定,即比值一定,则圆柱的体积与底面积成正比例。
②三角形的面积=底×高÷2,面积一定,即乘积一定,则三角形的底与高成反比例。
【点睛】掌握正、反比例的意义是解题的关键。
4. 9 7 正
【分析】根据比例的基本性质,先将等积式改写成比例式,再根据正、反比例的意义判定比例关系。
【详解】如果7x=9y
则x∶y=9∶7
x∶y
=9∶7
=
x∶y的比值一定,所以x和y成正比例关系。
【点睛】本题考查了比例的基本性质以及正、反比例的意义,两个相关联的量,若其比值一定,这两个量成正比例关系;若其乘积一定,这两个量成反比例关系。
5.正
【分析】两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的比值一定,这两种量就叫作成正比例的量,它们的关系叫作正比例关系,据此解答。
【详解】由“被除数÷除数=商”可知,被除数÷商=除数(一定),在没有余数的除法里,除数一定,被除数和商成正比例。
【点睛】本题主要考查正比例关系的辨识,掌握正比例关系的意义是解答题目的关键。
6. < 正
【分析】积一定,一个数乘的数越小其本身越大;x÷y=k(一定),x和y成正比例关系,据此分析。
【详解】如果(A,B都不为零),>,则A<B;,两边同时÷B÷,可得,A和B成正比例。
【点睛】关键是掌握分数乘法的计算方法,理解正比例的意义,商一定是正比例关系。
7. 总字数 时间 总字数 时间 比值 正比例
【分析】由表中数据可知,打字的总字数随着打字时间的变化而变化,经计算分析可知总字数与打字时间的比值是一个定值(60),据此可解答。
【详解】===…==60(比值一定)
在上表中,相关联的量是总字数和时间,总字数随着时间的变化而变化,比值是一定的。因此,总字数和时间成正比例。
故答案为:总字数,时间,总字数,时间,比值,正比例。
【点睛】本题考查了正比例的意义,关键是要掌握的正比例的意义:两个相关联变化的量,如果这两个量对应的数的比值一定,这两个量成正比例。
8.A
【详解】略
9.C
【详解】x=y
=
故答案为:C
10.B
【分析】
正比例:两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的比值一定(也就是商一定),这两种量成正比例关系。
【详解】A.a=b+3,则a-b=3(一定),差一定,a和b不成正比例;
B.a=5b,则a÷b=5(一定),商一定,a和b成正比例;
C.b=a-4,则a-b=4(一定),差一定,a和b不成正比例。
故答案为:B
11.C
【分析】
两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的比值一定,这两种量就叫做成正比例的量,它们的关系叫做正比例关系,据此解答。
【详解】A.正方形的面积=边长×边长,边长=面积÷边长,边长不一定,比值不一定,因此不符合题意;
B.儿童的身高和体重不相关,不符合题意;
C.播音的字数÷时间=播音的速度,一个播音员播音的速度一定,比值一定,符合题意。
因此一个播音员播音的速度一定,播音的字数和时间成正比例关系。
故答案为:C
12.A
【分析】依据正、反比例的意义,即若两个相关联的量的比值一定,则这两个量成正比例关系;若两个相关联的量的乘积一定,则这两个量成反比例关系,由此判断即可选择。
【详解】因为花的总钱数÷书的本数=书的价格(一定),是比值一定,所以花的总钱数与书的本数成正比例。
故答案为:A
13.A
【分析】因为在一定限度内,弹簧秤弹簧所挂物体的重量越大,伸长量也就越大,即弹簧的伸长与所挂物体的重量成正比例关系;又已知当挂上了3千克的物体,伸长约为1.5厘米,要求得挂上2.5千克的物体,伸长大约多少,设此时弹簧大约伸长x厘米,可列比例式:3∶1.5=2.5∶x,解这个比例即可。
【详解】解:设弹簧大约伸长x厘米。
3∶1.5=2.5∶x
3x=1.5×2.5
3x=3.75
x=3.75÷3
x=1.25
在这个弹簧秤上挂2.5千克的物体时,弹簧大约伸长1.25厘米。
故答案为:A
【点睛】需要理解弹簧秤的工作原理,能利用正比例关系列式,解决生活中的问题。
14.B
【解析】略
15.×
【详解】略
16.√
【分析】判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定,如果是比值一定,就成正比例,如果是乘积一定,则成反比例。
【详解】梯形的面积÷高=(上底+下底)÷2(一定),商一定,所以梯形的面积和高成正比例关系。所以原题说法正确。
故答案为:√
【点睛】此题属于辨识成正、反比例的量,就看这两个量是对应的比值一定,还是对应的乘积一定,再作判断。
17.×
【分析】依据在同时同地,物体的高度与它的影长的比值是一定的,所以此时可知物体的高度和影长是正比例关系,由于题干没说同时同地,据此即可判断。
【详解】由于在同时同地时物体的高度和影长成正比例,原说法错误。
故答案为:×
【点睛】此题属于辨识成正、反比例的量,就看这两个量是对应的比值一定,还是对应的乘积一定,再作判断。
18.×
【分析】根据x÷y=k(一定),x和y成正比例关系,进行分析。
【详解】如果“x+y=125”, x和y是加法关系,不成比例关系。
故答案为:×
【点睛】关键是理解正比例的意义,商一定是正比例关系。
19.√
【分析】两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的比值一定(也就是商一定),这两种量成正比例关系。
【详解】小麦的出粉率=×100%
小麦的出粉率一定,即比值一定,则小麦的总重量和面粉的重量成正比例关系。
故答案为:√
20. 3 6 200 20
【分析】两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的比值一定,这两种量就叫做成正比例的量,它们的关系叫做正比例关系,用字母表示为(一定)。先根据表中x和y两个量成正比例,当x=15时,y=25,求出y与x的比值;再用x×比值求出y,或用y÷比值求出x。
【详解】
当y=5时,x=5÷=5×=3。
当y=10时,x=10÷=10×=6。
当x=120时,y=120×=200。
当x=12时,y=12×=20。
如下表:
x 15 3 120 6 12
y 25 5 200 10 20
【点睛】明确正比例的意义是解决此题的关键。
21.(1)正
(2)香蕉
(3) 16 20
【分析】(1)总价=单价×数量,单价=总价÷数量,单价一定,总价和数量成正比例。
(2)求单价,单价=总价÷数量,代入计算后,比较大小即可。
(3)总价=单价×数量,代入即可。
【详解】(1)从图中获得信息,单价一定,苹果的总价和购买的数量成正比例。
(2)8÷1=8(元)
4÷1=4(元)
8>4,所以香蕉比苹果贵一些。
(3)8×2=16(元)
4×5=20(元)
所以苹果的总价和购买的数量成正比例,从图像上看,贵一些的水果是香蕉,买2千克香蕉需要16元,买5千克苹果需要20元。
【点睛】此题考查了正比例的量的应用知识,解答本题的关键是掌握正比例的概念。
22.11天
【分析】根据“照这样的速度”可知,看的页数∶看的天数=每天看的页数(一定),比值一定,则看的页数和看的天数成正比例关系,据此列出正比例方程,并求解。
【详解】解:设他看完这本课外书需要天。
275∶=75∶3
75=275×3
75=825
=825÷75
=11
答:他看完这本课外书需要11天。
【点睛】关键是判断题目中的两种相关联的量成什么比例关系,据此列出相应的比例方程。
23.18米
【分析】根据题意可知,同一时间,同一地点测得物体高度与影子长度的比值一定,那么物体高度与影子长度成正比例关系,即古树的高度∶古树的影长=标杆的长度∶标杆的影长,据此列出正比例方程,并求解。
【详解】解:设这棵古树高米。
∶10.8=3∶1.8
1.8=10.8×3
1.8=32.4
1.8÷1.8=32.4÷1.8
=18
答:这棵古树高18米。
【点睛】关键是判断题目中的两种相关联的量成什么比例关系,据此列出相应的比例方程。
24.(1)
树高/m 2 3 4 6 8 8.5
影长/m 1.6 2.4 3.2 4.8 6.4 6.8
(2)图见详解
发现:所描点在一条直线上;
(3)正;
(4)在
【分析】(1)求出影长与树高的比值,进而求出树高为8米和8.5米的影长;
(2)所描点在一条直线上;
(3)根据图像可以看出树高与影长成正比例;
(4)求出9.6与12的比值与1.6与2的的比值比较得结论。
【详解】(1)1.6÷2=0.8,2.4÷3=0.8,3.2÷4=0.8,
所以,8×0.8=6.4(米),8.5×0.8=6.8(米)
(2)如下图:
发现:所描点在一条直线上。
(3)因为影长与树高的比值是一定的,所以树高与影长成正比例;
(4)9.6∶12=0.8,1.6÷2=0.8
因为0.8=0.8,所以点(12,9.6),在这条直线上。
【点睛】此题考查的是正比例的判断和图像,解答此题关键是掌握正比例的意义。
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
