成都七中育才学校初2021级数学第1周课后练习(无答案)
文档属性
| 名称 | 成都七中育才学校初2021级数学第1周课后练习(无答案) |  | |
| 格式 | doc | ||
| 文件大小 | 344.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-31 07:52:04 | ||
图片预览

文档简介
成都七中育才学校初2021级数学第1周课后练习
一.选择题(共8小题)
1.下列各数中,比﹣3小的数是( )
A.﹣1 B.0 C.2 D.﹣4
2.下列图形中,既是轴对称图形又是中心对称图形的是( )
A. B. C. D.
3.据报道,华为某新款手机采用了5纳米制程芯片,5纳米就是0.000000005米,数据0.000000005用科学记数法表示为( )
A.5×10﹣8 B.5×10﹣9 C.0.5×10﹣8 D.0.5×10﹣9
4.下列计算正确的是( )
A.(﹣a)4÷a3=a B.(﹣x3y)2=x5y2
C.a2 a3=a6 D.(x﹣y)2=x2﹣y2
5.在平面直角坐标系中,点P(3,﹣2)关于x轴的对称点的坐标是( )
A.(﹣3,﹣2)B.(﹣3,2)C.(3,2) D.(﹣2,3)
6.如图,在直径为AB的⊙O中,点C,D在圆上,AC=CD,若∠CAD=28°,则∠DAB的度数为( )A.28° B.34° C.56° D.62°
7.为了保护环境加强环保教育,某中学组织学生参加义务收集废旧电池的活动,下面是随机抽取40名学生对收集废旧电池的数量进行的统计:
废旧电池数/节 4 5 6 7 8
人数/人 9 11 11 5 4
请根据学生收集到的废旧电池数,判断下列说法正确的是( )
A.样本为40名学生 B.众数是11节 C.中位数是6节 D.平均数是5.6节
8.已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论:
①b2>4ac;②abc<0;③2a+b﹣c>0;④a+b+c<0,其中正确的是( )
A.①④ B.②④ C.②③ D.①③④
二、填空题(答案写在答题卡上)
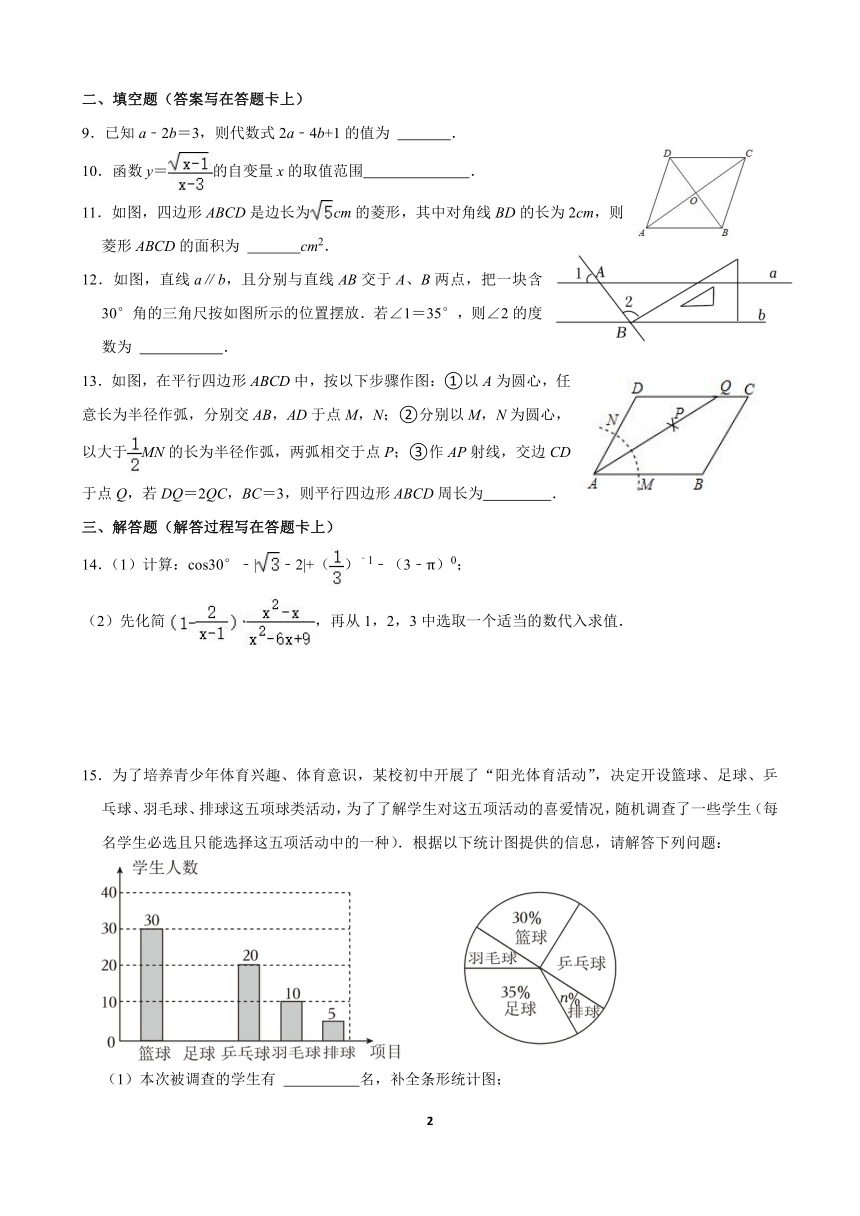
9.已知a﹣2b=3,则代数式2a﹣4b+1的值为 .
10.函数y=的自变量x的取值范围 .
11.如图,四边形ABCD是边长为cm的菱形,其中对角线BD的长为2cm,则菱形ABCD的面积为 cm2.
12.如图,直线a∥b,且分别与直线AB交于A、B两点,把一块含30°角的三角尺按如图所示的位置摆放.若∠1=35°,则∠2的度数为 .
13.如图,在平行四边形ABCD中,按以下步骤作图:①以A为圆心,任意长为半径作弧,分别交AB,AD于点M,N;②分别以M,N为圆心,以大于MN的长为半径作弧,两弧相交于点P;③作AP射线,交边CD于点Q,若DQ=2QC,BC=3,则平行四边形ABCD周长为 .
三、解答题(解答过程写在答题卡上)
14.(1)计算:cos30°﹣|﹣2|+()﹣1﹣(3﹣π)0;
(2)先化简,再从1,2,3中选取一个适当的数代入求值.
15.为了培养青少年体育兴趣、体育意识,某校初中开展了“阳光体育活动”,决定开设篮球、足球、乒乓球、羽毛球、排球这五项球类活动,为了了解学生对这五项活动的喜爱情况,随机调查了一些学生(每名学生必选且只能选择这五项活动中的一种).根据以下统计图提供的信息,请解答下列问题:
(1)本次被调查的学生有 名,补全条形统计图;
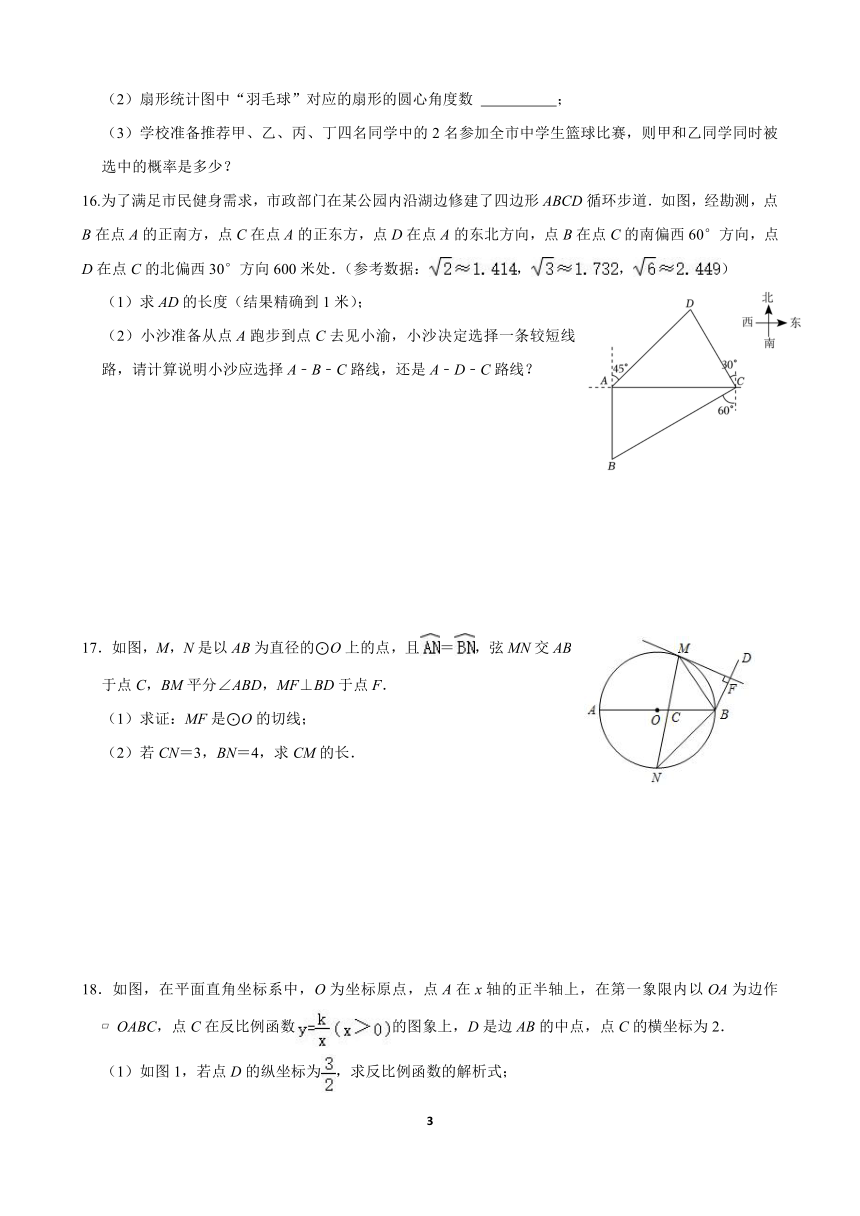
(2)扇形统计图中“羽毛球”对应的扇形的圆心角度数 ;
(3)学校准备推荐甲、乙、丙、丁四名同学中的2名参加全市中学生篮球比赛,则甲和乙同学同时被选中的概率是多少?
16.为了满足市民健身需求,市政部门在某公园内沿湖边修建了四边形ABCD循环步道.如图,经勘测,点B在点A的正南方,点C在点A的正东方,点D在点A的东北方向,点B在点C的南偏西60°方向,点D在点C的北偏西30°方向600米处.(参考数据:,,)
(1)求AD的长度(结果精确到1米);
(2)小沙准备从点A跑步到点C去见小渝,小沙决定选择一条较短线路,请计算说明小沙应选择A﹣B﹣C路线,还是A﹣D﹣C路线?
17.如图,M,N是以AB为直径的⊙O上的点,且=,弦MN交AB于点C,BM平分∠ABD,MF⊥BD于点F.
(1)求证:MF是⊙O的切线;
(2)若CN=3,BN=4,求CM的长.
如图,在平面直角坐标系中,O为坐标原点,点A在x轴的正半轴上,在第一象限内以OA为边作 OABC,点C在反比例函数的图象上,D是边AB的中点,点C的横坐标为2.
(1)如图1,若点D的纵坐标为,求反比例函数的解析式;
(2)如图2,若点D在反比例函数图象上且△OCD~△CDB,求 OABC的面积.
(3)如图3,在(1)的条件下,将直线l1:y=﹣x向上平移得到直线l2,直线l2与双曲线交于M1,M2两点,点P为M1M2的中点,过点M1作M1N⊥l1于点N.试探究的值是否为定值,若是定值,请求出这个定值;若不是定值,请说明理由.
B卷
填空题(共5小题)
19.若5xa﹣2y3与﹣3x4yb是同类项,则a+b的值为 .
20.若a,b是一元二次方程x2﹣5x﹣2=0的两个实数根,则的值为 .
21.如图,由四个全等的直角三角形与中间的一个小正方形EFGH拼成一个大正方形ABCD,连接AF和CH,AF=AB.现随机向正方形ABCD内掷一枚小针,则针尖落在阴影区域的概率为 .
22.在平面直角坐标系xOy中,直线y=mx+n分别交y轴负半轴,反比例函数y=(k>0,x>0)的图象于点A,B,以B为圆心,AB长为半径画弧,交平行于x轴的直线AE于点C.作CD垂直于x轴交反比例函数y=(k>0,x>0)的图象于点D.若,△BCD的面积为2,则k的值等于 .
23.如图,将直角△ABC沿斜边AC翻折后B点的对应点B',点P、Q是线段AB、B'C上的动点,且BP=B'Q,已知AB=12,BC=5,则线段PQ的最小值为 .
二、解答题
24.某地爆发新一波的疫情,疫情期间为保障市民正常生活,现要用10辆汽车装运蔬菜和水果到该地,每辆汽车只能装运同一种物资且必须装满,根据表提供的信息,解答下列问题:
物资种类 蔬菜 水果
每辆汽车运载量/吨 m m﹣2
每吨所需运费/元 100 120
(1)已知1辆车所装蔬菜的重量与2辆车所装水果的重量之和为14吨,求m的值;
(2)在(1)的条件下,设装运蔬菜的车辆有x辆,运输这批物资所需总运费为y元,求y与x之间的函数关系式;并求当装运蔬菜的车辆数不少于装运水果的车辆数的2倍时,总运费至少需要多少元?
25.抛物线y=﹣x2+bx+c与x轴分别交于点A,点B(3,0),与y轴交于点C(0,3).
(1)求抛物线的解析式;
(2)点D是直线BC上方抛物线上一动点,连接AD,交BC于点E,若AE=2ED,求点D的坐标;
26.已知正方形ABCD的边长为6,动点E,F分别在边AB,CD上运动,连接EF.
(1)如图1,过B作BG⊥EF交边AD于点G,交EF于点H.
i)若G为AD的中点,H为BG的中点,求AE的长;
ⅱ)探索线段AE,DG,CF之间的数量关系,写出你的结论并证明.
(2)如图2,将四边形EBCF沿EF翻折得到四边形EB′C′F,B′E与AD相交于点P,调整点E和点F的位置使得线段B′C′始终经过顶点D.
i)若点D到EF的距离,求DP的长;
ⅱ)点B′到AD的距离是否存在最大值?若存在,请直接写出这个最大距离;若不存在,请说明理
1
一.选择题(共8小题)
1.下列各数中,比﹣3小的数是( )
A.﹣1 B.0 C.2 D.﹣4
2.下列图形中,既是轴对称图形又是中心对称图形的是( )
A. B. C. D.
3.据报道,华为某新款手机采用了5纳米制程芯片,5纳米就是0.000000005米,数据0.000000005用科学记数法表示为( )
A.5×10﹣8 B.5×10﹣9 C.0.5×10﹣8 D.0.5×10﹣9
4.下列计算正确的是( )
A.(﹣a)4÷a3=a B.(﹣x3y)2=x5y2
C.a2 a3=a6 D.(x﹣y)2=x2﹣y2
5.在平面直角坐标系中,点P(3,﹣2)关于x轴的对称点的坐标是( )
A.(﹣3,﹣2)B.(﹣3,2)C.(3,2) D.(﹣2,3)
6.如图,在直径为AB的⊙O中,点C,D在圆上,AC=CD,若∠CAD=28°,则∠DAB的度数为( )A.28° B.34° C.56° D.62°
7.为了保护环境加强环保教育,某中学组织学生参加义务收集废旧电池的活动,下面是随机抽取40名学生对收集废旧电池的数量进行的统计:
废旧电池数/节 4 5 6 7 8
人数/人 9 11 11 5 4
请根据学生收集到的废旧电池数,判断下列说法正确的是( )
A.样本为40名学生 B.众数是11节 C.中位数是6节 D.平均数是5.6节
8.已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论:
①b2>4ac;②abc<0;③2a+b﹣c>0;④a+b+c<0,其中正确的是( )
A.①④ B.②④ C.②③ D.①③④
二、填空题(答案写在答题卡上)
9.已知a﹣2b=3,则代数式2a﹣4b+1的值为 .
10.函数y=的自变量x的取值范围 .
11.如图,四边形ABCD是边长为cm的菱形,其中对角线BD的长为2cm,则菱形ABCD的面积为 cm2.
12.如图,直线a∥b,且分别与直线AB交于A、B两点,把一块含30°角的三角尺按如图所示的位置摆放.若∠1=35°,则∠2的度数为 .
13.如图,在平行四边形ABCD中,按以下步骤作图:①以A为圆心,任意长为半径作弧,分别交AB,AD于点M,N;②分别以M,N为圆心,以大于MN的长为半径作弧,两弧相交于点P;③作AP射线,交边CD于点Q,若DQ=2QC,BC=3,则平行四边形ABCD周长为 .
三、解答题(解答过程写在答题卡上)
14.(1)计算:cos30°﹣|﹣2|+()﹣1﹣(3﹣π)0;
(2)先化简,再从1,2,3中选取一个适当的数代入求值.
15.为了培养青少年体育兴趣、体育意识,某校初中开展了“阳光体育活动”,决定开设篮球、足球、乒乓球、羽毛球、排球这五项球类活动,为了了解学生对这五项活动的喜爱情况,随机调查了一些学生(每名学生必选且只能选择这五项活动中的一种).根据以下统计图提供的信息,请解答下列问题:
(1)本次被调查的学生有 名,补全条形统计图;
(2)扇形统计图中“羽毛球”对应的扇形的圆心角度数 ;
(3)学校准备推荐甲、乙、丙、丁四名同学中的2名参加全市中学生篮球比赛,则甲和乙同学同时被选中的概率是多少?
16.为了满足市民健身需求,市政部门在某公园内沿湖边修建了四边形ABCD循环步道.如图,经勘测,点B在点A的正南方,点C在点A的正东方,点D在点A的东北方向,点B在点C的南偏西60°方向,点D在点C的北偏西30°方向600米处.(参考数据:,,)
(1)求AD的长度(结果精确到1米);
(2)小沙准备从点A跑步到点C去见小渝,小沙决定选择一条较短线路,请计算说明小沙应选择A﹣B﹣C路线,还是A﹣D﹣C路线?
17.如图,M,N是以AB为直径的⊙O上的点,且=,弦MN交AB于点C,BM平分∠ABD,MF⊥BD于点F.
(1)求证:MF是⊙O的切线;
(2)若CN=3,BN=4,求CM的长.
如图,在平面直角坐标系中,O为坐标原点,点A在x轴的正半轴上,在第一象限内以OA为边作 OABC,点C在反比例函数的图象上,D是边AB的中点,点C的横坐标为2.
(1)如图1,若点D的纵坐标为,求反比例函数的解析式;
(2)如图2,若点D在反比例函数图象上且△OCD~△CDB,求 OABC的面积.
(3)如图3,在(1)的条件下,将直线l1:y=﹣x向上平移得到直线l2,直线l2与双曲线交于M1,M2两点,点P为M1M2的中点,过点M1作M1N⊥l1于点N.试探究的值是否为定值,若是定值,请求出这个定值;若不是定值,请说明理由.
B卷
填空题(共5小题)
19.若5xa﹣2y3与﹣3x4yb是同类项,则a+b的值为 .
20.若a,b是一元二次方程x2﹣5x﹣2=0的两个实数根,则的值为 .
21.如图,由四个全等的直角三角形与中间的一个小正方形EFGH拼成一个大正方形ABCD,连接AF和CH,AF=AB.现随机向正方形ABCD内掷一枚小针,则针尖落在阴影区域的概率为 .
22.在平面直角坐标系xOy中,直线y=mx+n分别交y轴负半轴,反比例函数y=(k>0,x>0)的图象于点A,B,以B为圆心,AB长为半径画弧,交平行于x轴的直线AE于点C.作CD垂直于x轴交反比例函数y=(k>0,x>0)的图象于点D.若,△BCD的面积为2,则k的值等于 .
23.如图,将直角△ABC沿斜边AC翻折后B点的对应点B',点P、Q是线段AB、B'C上的动点,且BP=B'Q,已知AB=12,BC=5,则线段PQ的最小值为 .
二、解答题
24.某地爆发新一波的疫情,疫情期间为保障市民正常生活,现要用10辆汽车装运蔬菜和水果到该地,每辆汽车只能装运同一种物资且必须装满,根据表提供的信息,解答下列问题:
物资种类 蔬菜 水果
每辆汽车运载量/吨 m m﹣2
每吨所需运费/元 100 120
(1)已知1辆车所装蔬菜的重量与2辆车所装水果的重量之和为14吨,求m的值;
(2)在(1)的条件下,设装运蔬菜的车辆有x辆,运输这批物资所需总运费为y元,求y与x之间的函数关系式;并求当装运蔬菜的车辆数不少于装运水果的车辆数的2倍时,总运费至少需要多少元?
25.抛物线y=﹣x2+bx+c与x轴分别交于点A,点B(3,0),与y轴交于点C(0,3).
(1)求抛物线的解析式;
(2)点D是直线BC上方抛物线上一动点,连接AD,交BC于点E,若AE=2ED,求点D的坐标;
26.已知正方形ABCD的边长为6,动点E,F分别在边AB,CD上运动,连接EF.
(1)如图1,过B作BG⊥EF交边AD于点G,交EF于点H.
i)若G为AD的中点,H为BG的中点,求AE的长;
ⅱ)探索线段AE,DG,CF之间的数量关系,写出你的结论并证明.
(2)如图2,将四边形EBCF沿EF翻折得到四边形EB′C′F,B′E与AD相交于点P,调整点E和点F的位置使得线段B′C′始终经过顶点D.
i)若点D到EF的距离,求DP的长;
ⅱ)点B′到AD的距离是否存在最大值?若存在,请直接写出这个最大距离;若不存在,请说明理
1
