【备课参考】2015秋冀教版数学八上课件17.1等腰三角形(共26张PPT)
文档属性
| 名称 | 【备课参考】2015秋冀教版数学八上课件17.1等腰三角形(共26张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-10-04 14:21:16 | ||
图片预览



文档简介
课件26张PPT。17.1《等腰三角形》
图中有些你熟悉的图形吗?
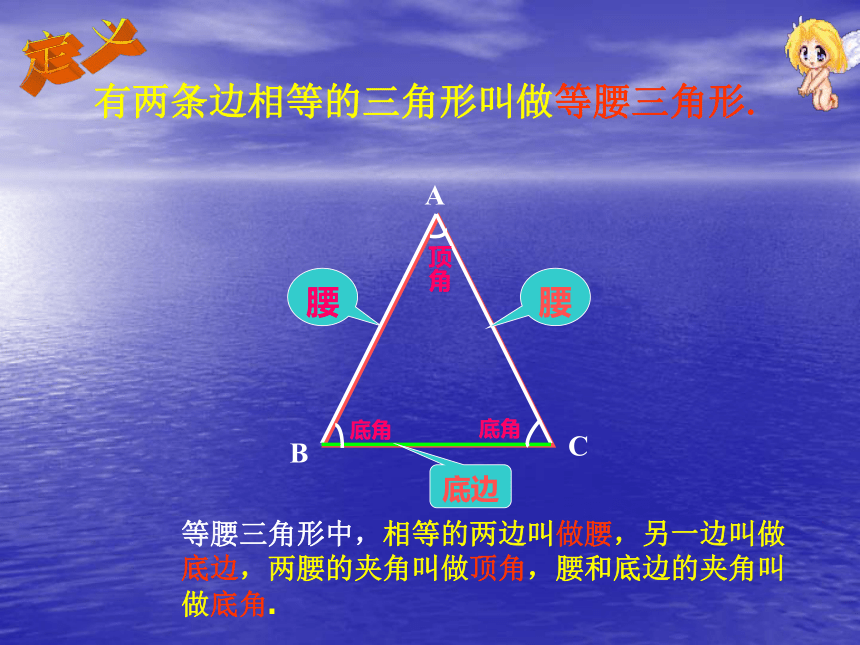
图中有些你熟悉的图形吗?它们有什么共同特点?北京五塔寺西安半坡博物馆斜拉桥梁体育观看台架埃及金字塔有两条边相等的三角形叫做等腰三角形. 等腰三角形中,相等的两边叫做腰,另一边叫做底边,两腰的夹角叫做顶角,腰和底边的夹角叫做底角.底边定义AB、ACBC∠B、 ∠CCA、CBAC∠A、 ∠BAC、AD∠ACD、 ∠ADCDC
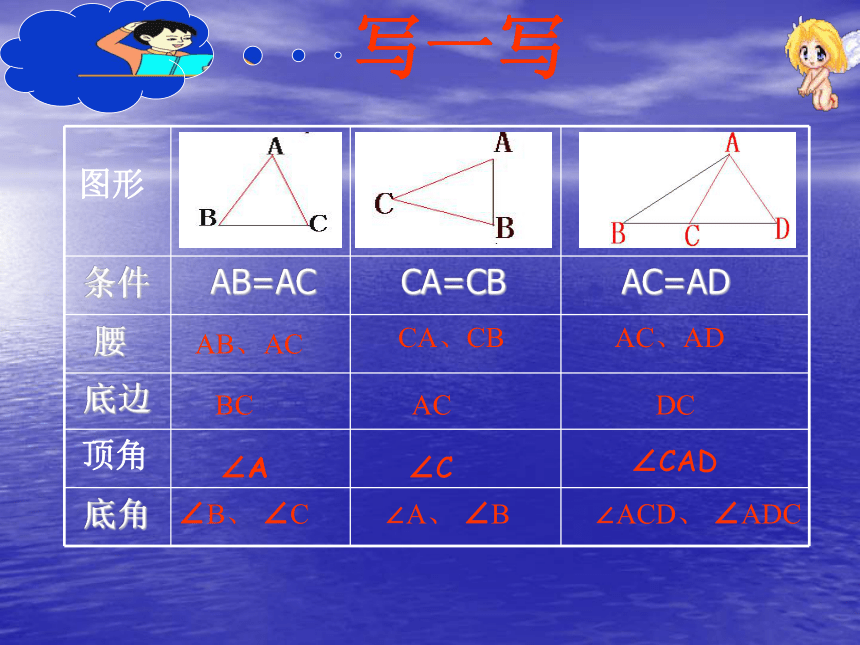
图形顶角∠A∠C∠CAD写一写
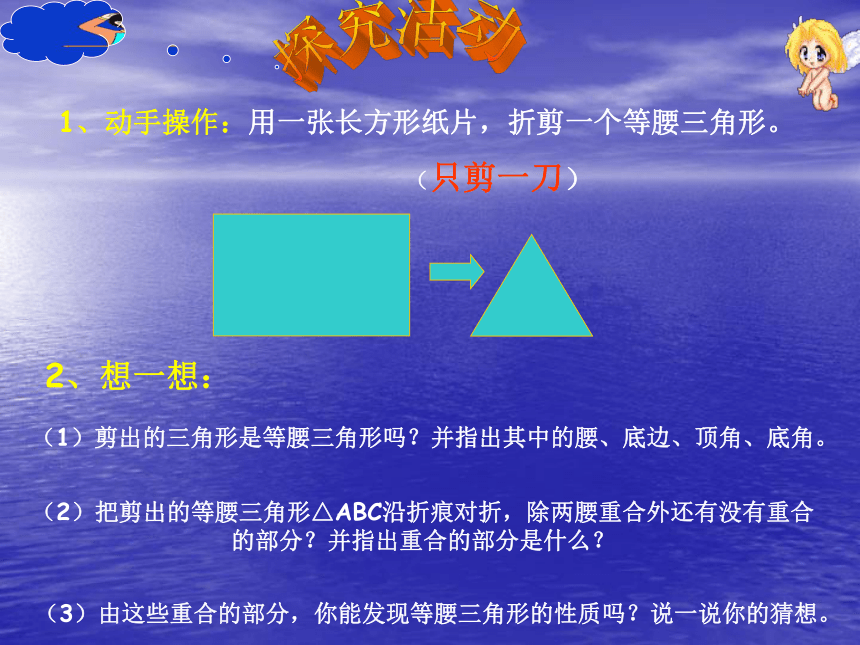
探究活动1、动手操作:用一张长方形纸片,折剪一个等腰三角形。
(只剪一刀)2、想一想: (1)剪出的三角形是等腰三角形吗?并指出其中的腰、底边、顶角、底角。(2)把剪出的等腰三角形△ABC沿折痕对折,除两腰重合外还有没有重合的部分?并指出重合的部分是什么? (3)由这些重合的部分,你能发现等腰三角形的性质吗?说一说你的猜想。
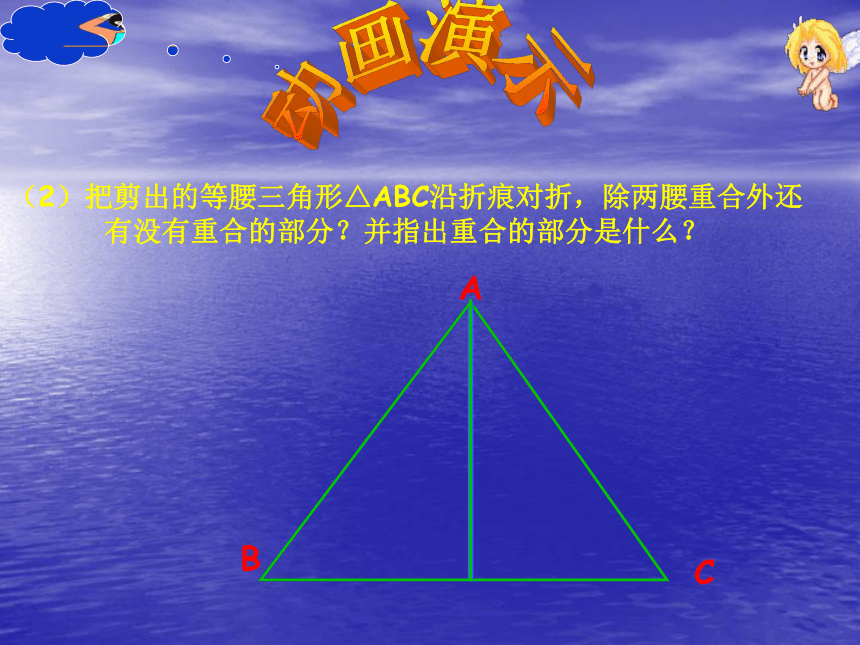
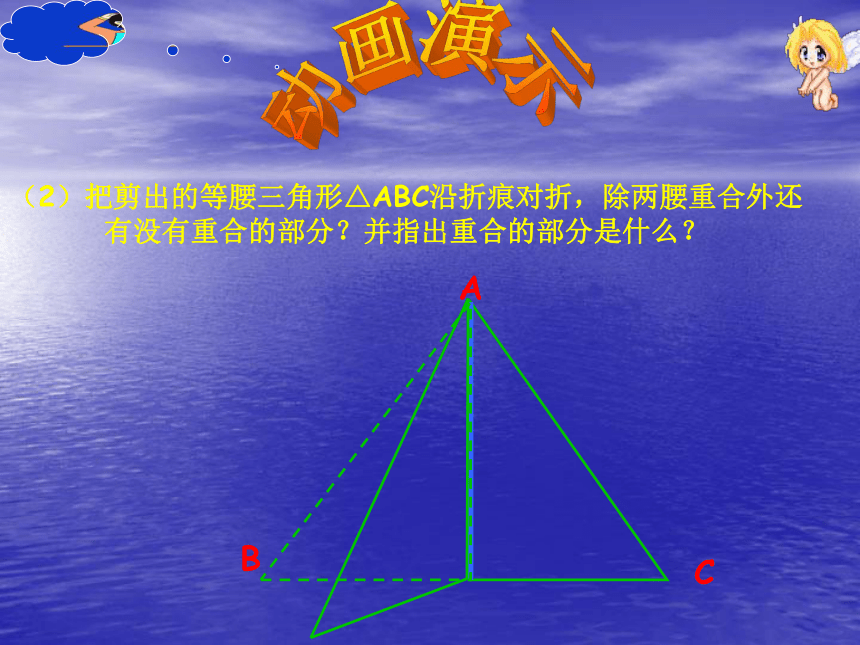
动画演示ABC(2)把剪出的等腰三角形△ABC沿折痕对折,除两腰重合外还有没有重合的部分?并指出重合的部分是什么?
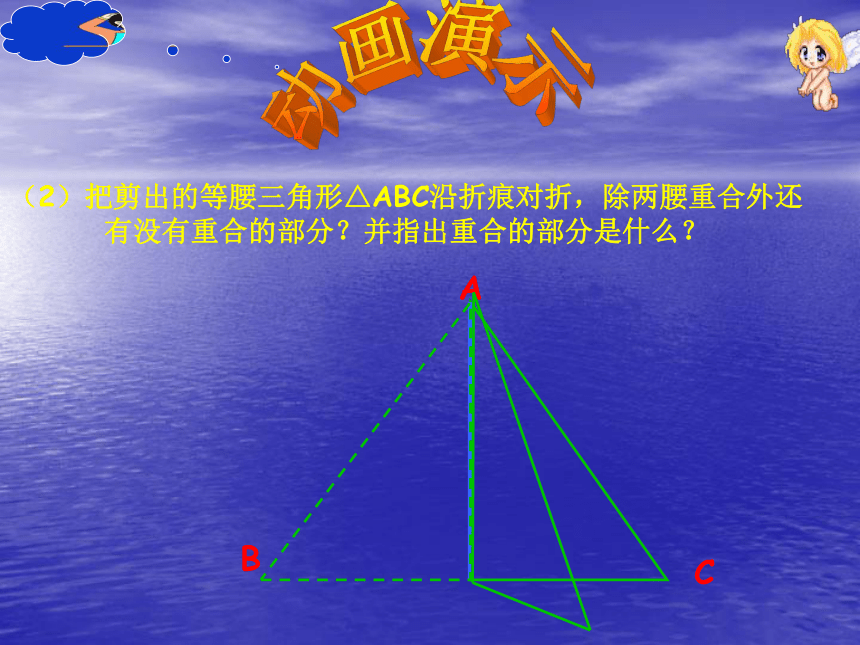
动画演示ABC(2)把剪出的等腰三角形△ABC沿折痕对折,除两腰重合外还有没有重合的部分?并指出重合的部分是什么?
动画演示ABC(2)把剪出的等腰三角形△ABC沿折痕对折,除两腰重合外还有没有重合的部分?并指出重合的部分是什么?
动画演示ABC(2)把剪出的等腰三角形△ABC沿折痕对折,除两腰重合外还有没有重合的部分?并指出重合的部分是什么?
动画演示ABC(2)把剪出的等腰三角形△ABC沿折痕对折,除两腰重合外还有没有重合的部分?并指出重合的部分是什么?
动画演示ABC(2)把剪出的等腰三角形△ABC沿折痕对折,除两腰重合外还有没有重合的部分?并指出重合的部分是什么?
动画演示ABC(2)把剪出的等腰三角形△ABC沿折痕对折,除两腰重合外还有没有重合的部分?并指出重合的部分是什么?
动画演示ABC(2)把剪出的等腰三角形△ABC沿折痕对折,除两腰重合外还有没有重合的部分?并指出重合的部分是什么?
动画演示ABC(2)把剪出的等腰三角形△ABC沿折痕对折,除两腰重合外还有没有重合的部分?并指出重合的部分是什么?
动画演示ABC(2)把剪出的等腰三角形△ABC沿折痕对折,除两腰重合外还有没有重合的部分?并指出重合的部分是什么?
动画演示AC(2)把剪出的等腰三角形△ABC沿折痕对折,除两腰重合外还有没有重合的部分?并指出重合的部分是什么? 底角
你发现了什么?结论:等腰三角形的两底角相等
探知求证:性质1、等腰三角形的两个底角相等。
(等边对等角)ABCD已知: △ABC 中,AB=AC
证明:作底边BC边上的中线AD。
在△ABD与△ACD中:
AB=AC(已知)
BD=DC(作图)
AD=AD(公共边)
∴△ABD≌△ACD(SSS)
∴∠B=∠C(全等三角形对应角相等)
性质1的应用格式:
∵AB=AC(已知) ∴∠B=∠C(等边对等角)求证:∠B=∠C 。
证法欣赏方法一:作顶角∠BAC的平分线AD。
∵AD平分∠BAC
∴∠1=∠2
在△ABD与△ACD中
AB=AC(已知)
∠1=∠2(已证)
AD=AD(公共边)
∴ △ABD ≌ △ACD(SAS)
∴ ∠B=∠C
ACB`D方法二:作底边BC的高AD。
∵AD⊥BC
∴ ∠ADB =∠ADC=90°
在Rt△ABD与Rt△ACD中
AB=AC(已知)
AD=AD(公共边)
∴ △ABD ≌ △ACD(HL)
∴ ∠B=∠C
112AB CD议一议:说说为什么在添加辅助时,作顶角平分线,
底边中线,底边高都能使分成的两个三角形全等?
性质2:等腰三角形的顶角平分线,底边上的中线,底边上的高互相重合。(通常说成等腰三角形的“三线合一”)性质2可分解成下面三个方面来理解:1、等腰三角形的顶角的平分线,既是底边上的中线,又是底边上的高。应用格式:∵AB=AC ∠1=∠2(已知)
∴BD=DC AD⊥BC(等腰三角形三线合一)2、等腰三角形的底边上中线,既是底边上的高,又是顶角平分线。应用格式:∵AB=AC BD=DC (已知)
∴AD⊥BC ∠1=∠2 (等腰三角形三线合一)
3、等腰三角形的底边上的高,既是底边上的中线,又是顶角平分线。应用格式:∵AB=AC AD⊥BC (已知)
∴BD=DC ∠1=∠2 (等腰三角形三线合一)
ABCD21
巩固练习1、练一练(基础训练)。
(1)已知等腰三形的一个顶角为36° ,则它的两个底角
分别为 。(2)已知等腰三角形的一个角为40°,则其它两个角
分别为 或 。 (3)已知等腰三角形的一个外角为70°,则这个三角形的
三个内角分别为 。(4)△ABC中,AB=AC,D在AC上,且BD=BC=AD 。①图中有 个等腰三角形,它们分别为
。② △ABC的三个内角分别为 。336°、72°、72°X2XX2X72° 、72°70° 、70°40° 、100°110° 、35° 、35°△ABC、△ADB、△DBC
能力训练△ABC中,AB=AC,D是BC边上的中点,
DF⊥AC于F DE ⊥ AB 于E .求证:DE=DF。ABCDEF 证明: ∵DE⊥AB,DF⊥AC(已知)
∴∠BED=∠CFD
又∵D是BC中点(已知)
∴BD=DC
∵AB=AC(已知)
∴∠B=∠C(等边对等角)
在△DBE与△DCF中
∠DEB=∠DFC(已证)
∠B=∠C(已证)
BD=DC(已证)
∴ △BDE ≌ △CDF(AAS)
∴DE=DF 方法二:连AD 。
∵AB=AC,BD=DC(已知)
∴AD是∠BAC的平分线。
(等腰三角形三线合一)
又∵DE⊥AB DF⊥AC
∴DE=DF
(角平分线上的点到这个
角的两边距离相等)
小结:通过本节课的学习你有收获吗?1、本节主要教学知识是等腰三角形的两个性质。等腰三角形的性质内容应用格式性质1ABC性质2ABC等腰三角形的
两个底角相等 等腰三角形的顶角
平分线、底边上的
中线底边上的高
互相重合。∵AB=AC(已知)
∴∠B=∠C (等边对等角)①∵AB=AC,∠1=∠2(已知)
∴BD=DC,AD⊥BC(三线合一)
② ∵AB=AC,BD=DC(已知)
∴ ∠1=∠2, AD⊥BC(三线合一)
③∵ AB=AC, AD⊥BC (已知)
∴ ∠1=∠2, BD=DC(三线合一)D122、本节课学习了数学思想及方法:分类讨论和一题多解。
布置作业书面作业课后习题
图中有些你熟悉的图形吗?
图中有些你熟悉的图形吗?它们有什么共同特点?北京五塔寺西安半坡博物馆斜拉桥梁体育观看台架埃及金字塔有两条边相等的三角形叫做等腰三角形. 等腰三角形中,相等的两边叫做腰,另一边叫做底边,两腰的夹角叫做顶角,腰和底边的夹角叫做底角.底边定义AB、ACBC∠B、 ∠CCA、CBAC∠A、 ∠BAC、AD∠ACD、 ∠ADCDC
图形顶角∠A∠C∠CAD写一写
探究活动1、动手操作:用一张长方形纸片,折剪一个等腰三角形。
(只剪一刀)2、想一想: (1)剪出的三角形是等腰三角形吗?并指出其中的腰、底边、顶角、底角。(2)把剪出的等腰三角形△ABC沿折痕对折,除两腰重合外还有没有重合的部分?并指出重合的部分是什么? (3)由这些重合的部分,你能发现等腰三角形的性质吗?说一说你的猜想。
动画演示ABC(2)把剪出的等腰三角形△ABC沿折痕对折,除两腰重合外还有没有重合的部分?并指出重合的部分是什么?
动画演示ABC(2)把剪出的等腰三角形△ABC沿折痕对折,除两腰重合外还有没有重合的部分?并指出重合的部分是什么?
动画演示ABC(2)把剪出的等腰三角形△ABC沿折痕对折,除两腰重合外还有没有重合的部分?并指出重合的部分是什么?
动画演示ABC(2)把剪出的等腰三角形△ABC沿折痕对折,除两腰重合外还有没有重合的部分?并指出重合的部分是什么?
动画演示ABC(2)把剪出的等腰三角形△ABC沿折痕对折,除两腰重合外还有没有重合的部分?并指出重合的部分是什么?
动画演示ABC(2)把剪出的等腰三角形△ABC沿折痕对折,除两腰重合外还有没有重合的部分?并指出重合的部分是什么?
动画演示ABC(2)把剪出的等腰三角形△ABC沿折痕对折,除两腰重合外还有没有重合的部分?并指出重合的部分是什么?
动画演示ABC(2)把剪出的等腰三角形△ABC沿折痕对折,除两腰重合外还有没有重合的部分?并指出重合的部分是什么?
动画演示ABC(2)把剪出的等腰三角形△ABC沿折痕对折,除两腰重合外还有没有重合的部分?并指出重合的部分是什么?
动画演示ABC(2)把剪出的等腰三角形△ABC沿折痕对折,除两腰重合外还有没有重合的部分?并指出重合的部分是什么?
动画演示AC(2)把剪出的等腰三角形△ABC沿折痕对折,除两腰重合外还有没有重合的部分?并指出重合的部分是什么? 底角
你发现了什么?结论:等腰三角形的两底角相等
探知求证:性质1、等腰三角形的两个底角相等。
(等边对等角)ABCD已知: △ABC 中,AB=AC
证明:作底边BC边上的中线AD。
在△ABD与△ACD中:
AB=AC(已知)
BD=DC(作图)
AD=AD(公共边)
∴△ABD≌△ACD(SSS)
∴∠B=∠C(全等三角形对应角相等)
性质1的应用格式:
∵AB=AC(已知) ∴∠B=∠C(等边对等角)求证:∠B=∠C 。
证法欣赏方法一:作顶角∠BAC的平分线AD。
∵AD平分∠BAC
∴∠1=∠2
在△ABD与△ACD中
AB=AC(已知)
∠1=∠2(已证)
AD=AD(公共边)
∴ △ABD ≌ △ACD(SAS)
∴ ∠B=∠C
ACB`D方法二:作底边BC的高AD。
∵AD⊥BC
∴ ∠ADB =∠ADC=90°
在Rt△ABD与Rt△ACD中
AB=AC(已知)
AD=AD(公共边)
∴ △ABD ≌ △ACD(HL)
∴ ∠B=∠C
112AB CD议一议:说说为什么在添加辅助时,作顶角平分线,
底边中线,底边高都能使分成的两个三角形全等?
性质2:等腰三角形的顶角平分线,底边上的中线,底边上的高互相重合。(通常说成等腰三角形的“三线合一”)性质2可分解成下面三个方面来理解:1、等腰三角形的顶角的平分线,既是底边上的中线,又是底边上的高。应用格式:∵AB=AC ∠1=∠2(已知)
∴BD=DC AD⊥BC(等腰三角形三线合一)2、等腰三角形的底边上中线,既是底边上的高,又是顶角平分线。应用格式:∵AB=AC BD=DC (已知)
∴AD⊥BC ∠1=∠2 (等腰三角形三线合一)
3、等腰三角形的底边上的高,既是底边上的中线,又是顶角平分线。应用格式:∵AB=AC AD⊥BC (已知)
∴BD=DC ∠1=∠2 (等腰三角形三线合一)
ABCD21
巩固练习1、练一练(基础训练)。
(1)已知等腰三形的一个顶角为36° ,则它的两个底角
分别为 。(2)已知等腰三角形的一个角为40°,则其它两个角
分别为 或 。 (3)已知等腰三角形的一个外角为70°,则这个三角形的
三个内角分别为 。(4)△ABC中,AB=AC,D在AC上,且BD=BC=AD 。①图中有 个等腰三角形,它们分别为
。② △ABC的三个内角分别为 。336°、72°、72°X2XX2X72° 、72°70° 、70°40° 、100°110° 、35° 、35°△ABC、△ADB、△DBC
能力训练△ABC中,AB=AC,D是BC边上的中点,
DF⊥AC于F DE ⊥ AB 于E .求证:DE=DF。ABCDEF 证明: ∵DE⊥AB,DF⊥AC(已知)
∴∠BED=∠CFD
又∵D是BC中点(已知)
∴BD=DC
∵AB=AC(已知)
∴∠B=∠C(等边对等角)
在△DBE与△DCF中
∠DEB=∠DFC(已证)
∠B=∠C(已证)
BD=DC(已证)
∴ △BDE ≌ △CDF(AAS)
∴DE=DF 方法二:连AD 。
∵AB=AC,BD=DC(已知)
∴AD是∠BAC的平分线。
(等腰三角形三线合一)
又∵DE⊥AB DF⊥AC
∴DE=DF
(角平分线上的点到这个
角的两边距离相等)
小结:通过本节课的学习你有收获吗?1、本节主要教学知识是等腰三角形的两个性质。等腰三角形的性质内容应用格式性质1ABC性质2ABC等腰三角形的
两个底角相等 等腰三角形的顶角
平分线、底边上的
中线底边上的高
互相重合。∵AB=AC(已知)
∴∠B=∠C (等边对等角)①∵AB=AC,∠1=∠2(已知)
∴BD=DC,AD⊥BC(三线合一)
② ∵AB=AC,BD=DC(已知)
∴ ∠1=∠2, AD⊥BC(三线合一)
③∵ AB=AC, AD⊥BC (已知)
∴ ∠1=∠2, BD=DC(三线合一)D122、本节课学习了数学思想及方法:分类讨论和一题多解。
布置作业书面作业课后习题
同课章节目录
- 第十二章 分式和分式方程
- 12.1 分式
- 12.2 分式的乘除
- 12.3 分式的加减
- 12.4 分式方程
- 12.5 分式方程的应用
- 第十三章 全等三角形
- 13.1 命题与证明
- 13.2 全等图形
- 13.3 全等三角形的判定
- 13.4 三角形的尺规作图
- 第十四章 实数
- 14.1 平方根
- 14.2 立方根
- 14.3 实数
- 14.4 近似数
- 14.5 用计算器求平方根与立方根
- 第十五章 二次根式
- 15.1 二次根式
- 15.2 二次根式的乘除
- 15.3 二次根式的加减
- 15.4 二次根式的混合
- 第十六章 轴对称和中心对称
- 16.1 轴对称
- 16.2 线段的垂直平分
- 16.3 角的平分线
- 16.4 中心对称图形
- 16.5 利用图形的平移、旋转和轴对称设计图案
- 第十七章 特殊三角形
- 17.1 等腰三角形
- 17.2 直角三角形
- 17.3 勾股定理
- 17.4 直角三角形全等的判定
- 17.5 反证法
