【五环分层导学-课件】6-8 综合与实践:反比例函数应用之猜想、证明与推广-北师大版数学九(上)
文档属性
| 名称 | 【五环分层导学-课件】6-8 综合与实践:反比例函数应用之猜想、证明与推广-北师大版数学九(上) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-30 00:00:00 | ||
图片预览





文档简介
(共12张PPT)
第六章 反比例函数
第8课 综合与实践:反比例函数应用之猜想、证明与推广
北师大版九年级上册
本套资料以教育部颁布的《数学课程标准(2022)版》为依据,结合新中考改革研究,立足北师大版本教材开发,通过课堂流程的优化设计,内容的层次设计,循序渐进,让不同层次的学生都学有所问,问有所探,探有所获,能力都有不同层次的提高,思维不断生长。
新授课通过激活思维、探究新知、双基巩固、综合运用、分层反馈等环节来完成。
资料简介
【问题】某数学学习兴趣小组在学习时, 甲同学发现一个有趣的问题: 任意给定一个矩形, 是否存 在另一个矩形, 它的周长和面积分别是已知矩形周长和面积的 2 倍
【类比】乙同学说:“我们曾研究过一个类似的问题, 即任意给定一个正方形, 是否存在另一个正 方形, 它的周长和面积分别是已知正方形周长和面积的 2 倍 ”
(1) 设给定正方形的边长为 1 , 则其周长为 4 , 其面积为 1 ; 若另一个正方形周长是给定正方形周 长的 2 倍, 则其周长为 8 , 其边长为 2 , 则其面积为 4 . 故不存在这样的正方形.
(2) 推广到一般情况, 设给定正方形的边长为 , 则其周长为 , 其面积为 , 若另一个正方形周 长是给定正方形周长的 2 倍, 则其周长为 , 其边长为 , 面积为 . 故不存在这样的正方形. 请先从最简单情形人手, 再逐次递进,最后猜想得出结论, 然后应用结论解决问题.
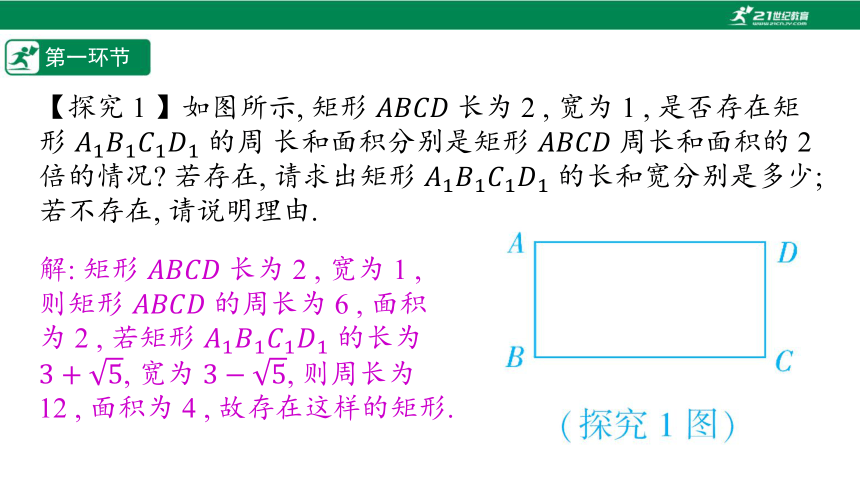
【探究 1 】如图所示, 矩形 长为 2 , 宽为 1 , 是否存在矩形 的周 长和面积分别是矩形 周长和面积的 2 倍的情况 若存在, 请求出矩形 的长和宽分别是多少; 若不存在, 请说明理由.
解: 矩形 长为 2 , 宽为 1 , 则矩形 的周长为 6 , 面积为 2 , 若矩形 的长为 , 宽为 , 则周长为 12 , 面积为 4 , 故存在这样的矩形.
【探究 2】如图所示, 矩形 长为 3 , 宽为 2 , 是否存在矩形 的周 长和面积分别是矩形 周长和面积的 2 倍的情况 若存在, 请求出矩形 的长和宽分别是多少; 若不存在, 请说明理由.
解: 矩形 长为 3 , 宽为 2 , 则矩形 的周长为 10 , 面积为 6 ,
若矩形 的长为 , 宽为 , 则周长为 20 , 面积为 12 , 故存在这样的矩形.
[一般情况 ]
已知: 矩形 长为 , 宽为 , 是否存在矩形 的周长和面积分别是矩形 周长 和面积的 2 倍的情况 若存在, 请求出矩形 的长和宽分别是多少; (用含 的代数 式表示即可)若不存在, 请说明理由.
解: 因为矩形 长为 , 宽为 , 所以矩形 的周长为 , 面积为 , 存在这样的矩形, 矩形 的长为 , 宽为 , 则周长为 , 面积为 .
[应用]
已知矩形 长为 30 , 宽为 13 , 若矩形 的周长和面积分别是矩形 周长和面积 的 2 倍, 则矩形 的长是 , 宽是 .
[解析] 矩形 长为 30 , 宽为 13 , 若矩形 的周长和面积分别是矩形 周长和面 积的 2 倍, 则矩形 的长是 , 宽为 .
故答案为 .
[问题提出] “任意给定一个矩形 , 是否存在另一矩形 , 它的周长和面积分别是已知矩形周长 和面积的三分之一 ”
为解决上面的问题,我们先来研究几种简单的情况.
(1) 已知矩形 的两邻边长分别为 12 和 1 , 是否存在另一个矩形 , 它的周长和面积分别是已知 矩形周长和面积的三分之一
解: 设所求矩形 的两邻边长分别是 和 , 由题意
消去 化简得 ,
解得 ,
已知矩形 的两邻边长分别为 12 和 1 时, 存在另一矩形 ,
它的周长和面积分别是已知矩形 周长和面积的三分之一.
(2) 如果已知矩形 的两邻边长分别为 6 和 2 , 请依照上面的方法研究: 是否存在满足要求的矩 形
解: 设所求矩形 的两邻边长分别是 和 , 由题意得
消去 化简得 ,
方程 没有实数解,
已知矩形 的两邻边长分别为 6 和 2 时, 不存在另一矩形 , 它的周长和面积分别是已知矩形 周长和面积的三分之一.
[问题解决] 如果已知矩形 的两邻边长分别为 和 , 请你研究, 当 和 满足什么条件时, 矩 形 存在
解: 设所求矩形 的两邻边长分别是 和 , 由题意得
消去 化简得 , ,
当 时, , 方程有实数解,
当 和 满足 时,矩形 存在.
[应用提升] 如果在同一平面直角坐标系中画出了一次函数和反比例函数的部 分图像如图所示, 其中 和 分别表示矩形 的两邻边长, 请你结合刚才的研 究, 回答下面的问题.
(1)该图像所表示矩形 的两邻边长各为多少
(2)该图像所表示矩形 的两邻边长各为多少
解 : (1)一次函数解析式为 , 反比例函数解析式为 ,
设矩形 的两邻边长分别为 和 , 则 , 解得
, 该图像所表示矩形 的两邻边长分别为 15 和 .
(2)方程组 消去 化简得 ,
,
该图像所表示矩形 的两邻边长分别为 和 3 .
第六章 反比例函数
第8课 综合与实践:反比例函数应用之猜想、证明与推广
北师大版九年级上册
本套资料以教育部颁布的《数学课程标准(2022)版》为依据,结合新中考改革研究,立足北师大版本教材开发,通过课堂流程的优化设计,内容的层次设计,循序渐进,让不同层次的学生都学有所问,问有所探,探有所获,能力都有不同层次的提高,思维不断生长。
新授课通过激活思维、探究新知、双基巩固、综合运用、分层反馈等环节来完成。
资料简介
【问题】某数学学习兴趣小组在学习时, 甲同学发现一个有趣的问题: 任意给定一个矩形, 是否存 在另一个矩形, 它的周长和面积分别是已知矩形周长和面积的 2 倍
【类比】乙同学说:“我们曾研究过一个类似的问题, 即任意给定一个正方形, 是否存在另一个正 方形, 它的周长和面积分别是已知正方形周长和面积的 2 倍 ”
(1) 设给定正方形的边长为 1 , 则其周长为 4 , 其面积为 1 ; 若另一个正方形周长是给定正方形周 长的 2 倍, 则其周长为 8 , 其边长为 2 , 则其面积为 4 . 故不存在这样的正方形.
(2) 推广到一般情况, 设给定正方形的边长为 , 则其周长为 , 其面积为 , 若另一个正方形周 长是给定正方形周长的 2 倍, 则其周长为 , 其边长为 , 面积为 . 故不存在这样的正方形. 请先从最简单情形人手, 再逐次递进,最后猜想得出结论, 然后应用结论解决问题.
【探究 1 】如图所示, 矩形 长为 2 , 宽为 1 , 是否存在矩形 的周 长和面积分别是矩形 周长和面积的 2 倍的情况 若存在, 请求出矩形 的长和宽分别是多少; 若不存在, 请说明理由.
解: 矩形 长为 2 , 宽为 1 , 则矩形 的周长为 6 , 面积为 2 , 若矩形 的长为 , 宽为 , 则周长为 12 , 面积为 4 , 故存在这样的矩形.
【探究 2】如图所示, 矩形 长为 3 , 宽为 2 , 是否存在矩形 的周 长和面积分别是矩形 周长和面积的 2 倍的情况 若存在, 请求出矩形 的长和宽分别是多少; 若不存在, 请说明理由.
解: 矩形 长为 3 , 宽为 2 , 则矩形 的周长为 10 , 面积为 6 ,
若矩形 的长为 , 宽为 , 则周长为 20 , 面积为 12 , 故存在这样的矩形.
[一般情况 ]
已知: 矩形 长为 , 宽为 , 是否存在矩形 的周长和面积分别是矩形 周长 和面积的 2 倍的情况 若存在, 请求出矩形 的长和宽分别是多少; (用含 的代数 式表示即可)若不存在, 请说明理由.
解: 因为矩形 长为 , 宽为 , 所以矩形 的周长为 , 面积为 , 存在这样的矩形, 矩形 的长为 , 宽为 , 则周长为 , 面积为 .
[应用]
已知矩形 长为 30 , 宽为 13 , 若矩形 的周长和面积分别是矩形 周长和面积 的 2 倍, 则矩形 的长是 , 宽是 .
[解析] 矩形 长为 30 , 宽为 13 , 若矩形 的周长和面积分别是矩形 周长和面 积的 2 倍, 则矩形 的长是 , 宽为 .
故答案为 .
[问题提出] “任意给定一个矩形 , 是否存在另一矩形 , 它的周长和面积分别是已知矩形周长 和面积的三分之一 ”
为解决上面的问题,我们先来研究几种简单的情况.
(1) 已知矩形 的两邻边长分别为 12 和 1 , 是否存在另一个矩形 , 它的周长和面积分别是已知 矩形周长和面积的三分之一
解: 设所求矩形 的两邻边长分别是 和 , 由题意
消去 化简得 ,
解得 ,
已知矩形 的两邻边长分别为 12 和 1 时, 存在另一矩形 ,
它的周长和面积分别是已知矩形 周长和面积的三分之一.
(2) 如果已知矩形 的两邻边长分别为 6 和 2 , 请依照上面的方法研究: 是否存在满足要求的矩 形
解: 设所求矩形 的两邻边长分别是 和 , 由题意得
消去 化简得 ,
方程 没有实数解,
已知矩形 的两邻边长分别为 6 和 2 时, 不存在另一矩形 , 它的周长和面积分别是已知矩形 周长和面积的三分之一.
[问题解决] 如果已知矩形 的两邻边长分别为 和 , 请你研究, 当 和 满足什么条件时, 矩 形 存在
解: 设所求矩形 的两邻边长分别是 和 , 由题意得
消去 化简得 , ,
当 时, , 方程有实数解,
当 和 满足 时,矩形 存在.
[应用提升] 如果在同一平面直角坐标系中画出了一次函数和反比例函数的部 分图像如图所示, 其中 和 分别表示矩形 的两邻边长, 请你结合刚才的研 究, 回答下面的问题.
(1)该图像所表示矩形 的两邻边长各为多少
(2)该图像所表示矩形 的两邻边长各为多少
解 : (1)一次函数解析式为 , 反比例函数解析式为 ,
设矩形 的两邻边长分别为 和 , 则 , 解得
, 该图像所表示矩形 的两邻边长分别为 15 和 .
(2)方程组 消去 化简得 ,
,
该图像所表示矩形 的两邻边长分别为 和 3 .
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
