【五环分层导学-课件】1-3 菱形的性质与综合运用-北师大版数学九(上)
文档属性
| 名称 | 【五环分层导学-课件】1-3 菱形的性质与综合运用-北师大版数学九(上) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-30 17:15:02 | ||
图片预览







文档简介
(共20张PPT)
第一章 特殊平行四边形
第3课 菱形的性质与综合运用
北师大版九年级上册
本套资料以教育部颁布的《数学课程标准(2022)版》为依据,结合新中考改革研究,立足北师大版本教材开发,通过课堂流程的优化设计,内容的层次设计,循序渐进,让不同层次的学生都学有所问,问有所探,探有所获,能力都有不同层次的提高,思维不断生长。
新授课通过激活思维、探究新知、双基巩固、综合运用、分层反馈五个环节来完成。
资料简介
第一环节 激活思维 通过回顾与本节新知有关的旧知或熟悉的生活情境,唤醒、激活学生的旧知,为新知生成奠定基础,为知识的形成提供情境。
第二环节 探究新知 通过一系列问题,引领学生通过自主、合作、探究的方式,在解决问题串的过程中,生成新知,积累基本活动经验,提高分析问题和解决问题的能力。
第三环节 双基巩固 通过典型例题,及时巩固基础知识与基本技能,为学生初步应用新知解决问题积累经验。
第四环节 综合运用 以本节知识为核心,设计一道综合题,提高学生综合运用知识的能力,发散思维,渗透数学思想方法。
第五环节 分层反馈 通过由易到难的当堂练习或检测,及时反馈学生掌握情况,给教师课后针对辅导与布置课后作业的量和难度提供数据参考。
五环导学
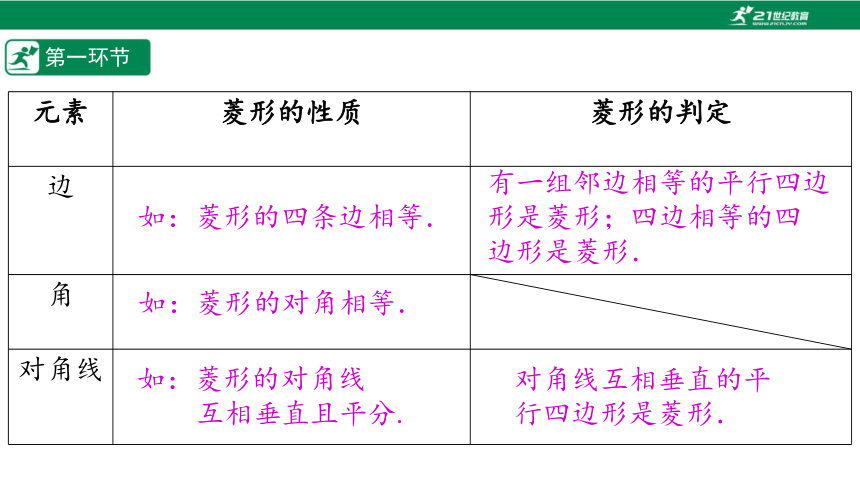
元素 菱形的性质 菱形的判定
边
角
对角线
如:菱形的四条边相等.
如:菱形的对角相等.
如:菱形的对角线
互相垂直且平分.
有一组邻边相等的平行四边形是菱形;四边相等的四
边形是菱形.
对角线互相垂直的平行四边形是菱形.
【问题1】如图,已知菱形ABCD的对角线AC=8,BD=6,求菱形ABCD的边长和面积?
解:根据题意,AO=4,OD=3,∠AOD=90°,
∴AD==5,
S菱形ABCD=2S△ADC=2×AC·OD=2××8×3=24.
C
A
B
D
O
问题一图
【问题2】如图,四边形ABCD 是边长为13cm 的菱形,AC 与BD 交于点E,对角线BD 长10cm.求菱形ABCD 的面积.
解: 四边形 是菱形,
菱形的边长为 ,
故菱形 的面积为 .
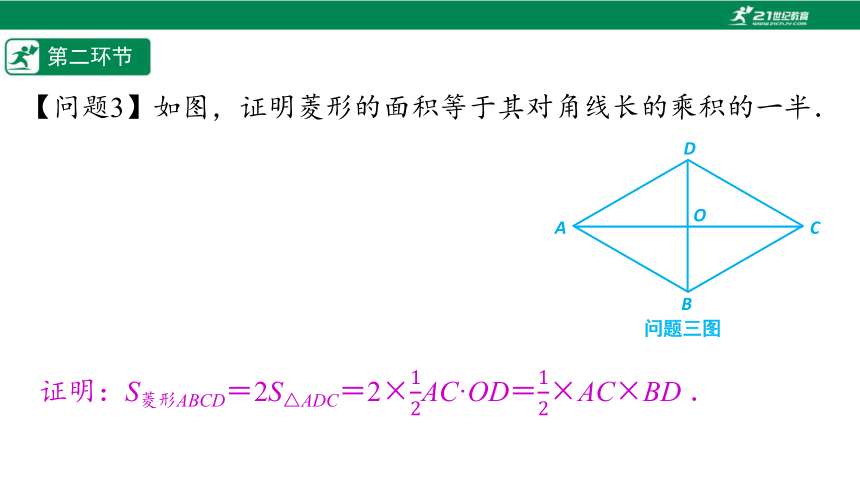
【问题3】如图,证明菱形的面积等于其对角线长的乘积的一半.
证明:S菱形ABCD=2S△ADC=2×AC·OD=×AC×BD .
C
A
B
D
O
问题三图
小结:菱形的面积=%// //%
对角线乘积的一半
【例题1】菱形ABCD 的周长为40 cm,它的一条对角线长10 cm.
(1)求这个菱形的每一个内角的度数.
(2)求这个菱形的面积.
(1) 如答图, 四边形 是菱形, 对角线 与 相交于点 .
菱形的周长为 .
一条对角线的长为 ,
令 , 则 ,
为等边三角形.
从而可知 .
(2) 四边形 是菱形, .
在 Rt 中, ,
,
菱形 的面积 .
【例题 2】如图, 两张等宽的长方形纸条交叉重叠在一起.
(1) 重叠的部分四边形 是 形, 请写出证明过程.
(2) 如果 , 连接 , 则 .
(3) 在 (2) 的条件下, 求四边形 的面积.
菱
解: (1) 证明如下: 如答图, 连接 .
四边形 是用两张等宽的长方形
纸条交叉重叠地放在一起而组成的图形,
,
四边形 是平行四边形
(两组对边分别平行的四边形是平行四边形).
过点 分别作 边上的高 , 垂足分别为 ,
则 (两纸条相同, 纸条宽度相同).
平行四边形 中, , 即 ,
.
平行四边形 为菱形 (有一组邻边相等的平行四边形是菱形).
(3) 在 Rt 中,
,
.
.
1.下列说法正确的是( )
A.对角线垂直的四边形是菱形
B.对角线互相平分的四边形是菱形
C.菱形的对角线相等且互相平分
D.菱形的对角线互相垂直且平分
D
2.如图, 在菱形 中, 对角线 交于点 , 且 , 过 点作 垂直于 , 交 于点 .
(1) 求 的长.
(2) 求 的值.
解: (1) 四边形 是菱形,
,
(2) 在 Rt 中, ,
的值为 .
3.如图, 在菱形 中, 对角线 交于点 , 且
, 过 点作 垂直于 , 交 于点 .
(1) 求 的长.
(2) 求 的值.
(1) 证明: 四边形 是平行四边形, .
.
四边形 是平行四边形.
四边形 是菱形.
(2) [ 解析] 连接 , 交 于 , 如答图所示.
四边形 是菱形,
.
,
,
. 故答案为 .
第一章 特殊平行四边形
第3课 菱形的性质与综合运用
北师大版九年级上册
本套资料以教育部颁布的《数学课程标准(2022)版》为依据,结合新中考改革研究,立足北师大版本教材开发,通过课堂流程的优化设计,内容的层次设计,循序渐进,让不同层次的学生都学有所问,问有所探,探有所获,能力都有不同层次的提高,思维不断生长。
新授课通过激活思维、探究新知、双基巩固、综合运用、分层反馈五个环节来完成。
资料简介
第一环节 激活思维 通过回顾与本节新知有关的旧知或熟悉的生活情境,唤醒、激活学生的旧知,为新知生成奠定基础,为知识的形成提供情境。
第二环节 探究新知 通过一系列问题,引领学生通过自主、合作、探究的方式,在解决问题串的过程中,生成新知,积累基本活动经验,提高分析问题和解决问题的能力。
第三环节 双基巩固 通过典型例题,及时巩固基础知识与基本技能,为学生初步应用新知解决问题积累经验。
第四环节 综合运用 以本节知识为核心,设计一道综合题,提高学生综合运用知识的能力,发散思维,渗透数学思想方法。
第五环节 分层反馈 通过由易到难的当堂练习或检测,及时反馈学生掌握情况,给教师课后针对辅导与布置课后作业的量和难度提供数据参考。
五环导学
元素 菱形的性质 菱形的判定
边
角
对角线
如:菱形的四条边相等.
如:菱形的对角相等.
如:菱形的对角线
互相垂直且平分.
有一组邻边相等的平行四边形是菱形;四边相等的四
边形是菱形.
对角线互相垂直的平行四边形是菱形.
【问题1】如图,已知菱形ABCD的对角线AC=8,BD=6,求菱形ABCD的边长和面积?
解:根据题意,AO=4,OD=3,∠AOD=90°,
∴AD==5,
S菱形ABCD=2S△ADC=2×AC·OD=2××8×3=24.
C
A
B
D
O
问题一图
【问题2】如图,四边形ABCD 是边长为13cm 的菱形,AC 与BD 交于点E,对角线BD 长10cm.求菱形ABCD 的面积.
解: 四边形 是菱形,
菱形的边长为 ,
故菱形 的面积为 .
【问题3】如图,证明菱形的面积等于其对角线长的乘积的一半.
证明:S菱形ABCD=2S△ADC=2×AC·OD=×AC×BD .
C
A
B
D
O
问题三图
小结:菱形的面积=%// //%
对角线乘积的一半
【例题1】菱形ABCD 的周长为40 cm,它的一条对角线长10 cm.
(1)求这个菱形的每一个内角的度数.
(2)求这个菱形的面积.
(1) 如答图, 四边形 是菱形, 对角线 与 相交于点 .
菱形的周长为 .
一条对角线的长为 ,
令 , 则 ,
为等边三角形.
从而可知 .
(2) 四边形 是菱形, .
在 Rt 中, ,
,
菱形 的面积 .
【例题 2】如图, 两张等宽的长方形纸条交叉重叠在一起.
(1) 重叠的部分四边形 是 形, 请写出证明过程.
(2) 如果 , 连接 , 则 .
(3) 在 (2) 的条件下, 求四边形 的面积.
菱
解: (1) 证明如下: 如答图, 连接 .
四边形 是用两张等宽的长方形
纸条交叉重叠地放在一起而组成的图形,
,
四边形 是平行四边形
(两组对边分别平行的四边形是平行四边形).
过点 分别作 边上的高 , 垂足分别为 ,
则 (两纸条相同, 纸条宽度相同).
平行四边形 中, , 即 ,
.
平行四边形 为菱形 (有一组邻边相等的平行四边形是菱形).
(3) 在 Rt 中,
,
.
.
1.下列说法正确的是( )
A.对角线垂直的四边形是菱形
B.对角线互相平分的四边形是菱形
C.菱形的对角线相等且互相平分
D.菱形的对角线互相垂直且平分
D
2.如图, 在菱形 中, 对角线 交于点 , 且 , 过 点作 垂直于 , 交 于点 .
(1) 求 的长.
(2) 求 的值.
解: (1) 四边形 是菱形,
,
(2) 在 Rt 中, ,
的值为 .
3.如图, 在菱形 中, 对角线 交于点 , 且
, 过 点作 垂直于 , 交 于点 .
(1) 求 的长.
(2) 求 的值.
(1) 证明: 四边形 是平行四边形, .
.
四边形 是平行四边形.
四边形 是菱形.
(2) [ 解析] 连接 , 交 于 , 如答图所示.
四边形 是菱形,
.
,
,
. 故答案为 .
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
