【五环分层导学-课件】2-10 一元二次方程应用之动态面积问题-北师大版数学九(上)
文档属性
| 名称 | 【五环分层导学-课件】2-10 一元二次方程应用之动态面积问题-北师大版数学九(上) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-30 17:15:02 | ||
图片预览






文档简介
(共16张PPT)
第二章 一元二次方程
第10课 一元一次方程应用之动态面积问题
北师大版九年级上册
本套资料以教育部颁布的《数学课程标准(2022)版》为依据,结合新中考改革研究,立足北师大版本教材开发,通过课堂流程的优化设计,内容的层次设计,循序渐进,让不同层次的学生都学有所问,问有所探,探有所获,能力都有不同层次的提高,思维不断生长。
新授课通过激活思维、探究新知、双基巩固、综合运用、分层反馈等环节来完成。
资料简介
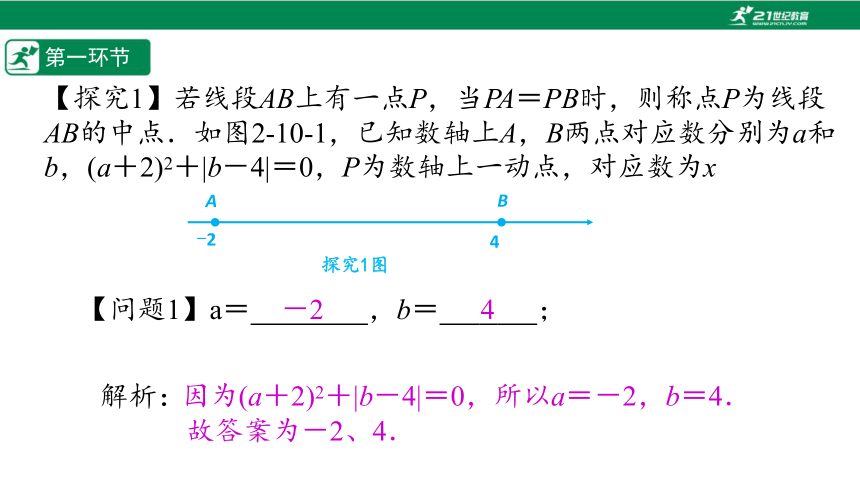
【探究1】若线段AB上有一点P,当PA=PB时,则称点P为线段AB的中点.如图2-10-1,已知数轴上A,B两点对应数分别为a和b,(a+2)2+|b-4|=0,P为数轴上一动点,对应数为x
【问题1】a=%/// /%,b=%// //%;
-2
A
4
B
探究1图
-2
4
解析:
因为(a+2)2+|b-4|=0,所以a=-2,b=4.
故答案为-2、4.
【问题2】若点P为线段AB的中点,
则P点对应的数x为%// //%.
若B为线段AP的中点时则P点对应的数x为%// //%.
1
10
解析:
若点P为线段AB的中点,则P点对应的数x为1.
若B为线段AP的中点时,AB=BP=6,
则P点对应的数x为10.
故答案为1、10.
【问题3】若点A、点B同时向左运动,它们的速度都为1个单位长度/秒,与此同时点P从-16处以2个单位长度/秒向右运动.
①设运动的时间为t秒,直接用含t的式子填空
AP= ;BP= .
|14-3t|
|20-3t|
②经过多长时间后,点A、点B、点P三点中其中一点是另外两点的中点?
解②t s后,点A的位置为:-2-t,
点B的位置为:4-t,点P的位置为:-16+2t.
当点A是PB的中点时,则-2-t-(-16+2t)=6,解得:t=;
当点P是AB的中点时,则-16+2t-(-2-t)=3,解得:t=;
当点B是PA的中点时,则-16+2t-(4-t)=6,解得:t=.
答:经过 s、 s、 s后,点A、点B、点P三点中其中一点是另外两点的中点.
C
Q
A
P
B
探究2图
【探究2】如图,在Rt△ABC中,∠C=90°,AC=30 cm,BC=25 cm,点P、Q分别从C、B点出发沿CA方向、BC方向匀速移动,速度分别是2 cm/s、1 cm/s,【问题1】经过t秒后点P,Q所走过的路程是%//// % ;%////% ;
PQ=%////% ;
2t cm
t cm
【问题2】求几秒后△PCQ的面积是△ACB面积的五分之二?
解(3)S△ACB=×AC×BC=×30×25=375,
∴S△ACB=×375=150.
又∵S△PCQ=×CQ×PC=×(25-t)×2t=25t-t2,
∴根据题意有:25t-t2=150,
∴化为一般式为t2-25t+150=0,解得t1=10,t2=15.
∴10秒或15秒后△PCQ的面积是△ACB面积的五分之二.
【问题3】利用方程解决此类实际问题的关键是?步骤是?
解:利用方程解决实际问题的关键是寻找等量关系. 步骤是:①审题;
②设未知数;
③利用等量关系列方程;
④解方程;
⑤检验;
⑥答.
1.如图,在Rt△ACB中,∠C=90°,点P,Q同时由A,B两点出发分别沿AC,BC方向向点C匀速移动(到点C为止),它们的速度都是1 m/s.经过几秒△PCQ的面积为Rt△ACB面积的一半?
C
P
Q
A
8m
B
6m
第1题图
解:设经过x秒后△PCQ的面积是Rt△ACB面积的一半,
则:(8-x)(6-x)=××6×8,
解得x1=12(不合题意,舍去),x2=2.
答:经2秒△PCQ的面积是Rt△ACB面积的一半.
2.(☆) 如图, 一次函数 的图像交 轴于点 , 交 轴于点 , 点 在线段 上(不与点 重合), 过点 分别作 和 的垂线, 垂足为 .
(1) 若点 的坐标为 , 那么
. (用含有 的代数 式表示)
(2) 在 (1) 的条件下, , (注意点 所在象限) . (用含 有 的代数式表示)
(3) 点 在何处时, 矩形 的面积为 1 请求出 的坐标.
第2题图
解: 由题意得 ,
整理得 , 解得 ,
故当 为 或 时, 矩形 的面积为 1 .
3.(☆) 如图, 由点 确定的 的面 积为 18 , 求 的值. 如果 呢
解 : 当 时, 如答图(1),
作 轴于点, ,
解得 .
第3题图
第3题答图①
当 时, 如答图 (2), 过点 作 轴于 .
解得 或 12 , 都不符合题意, 均舍去.
第3题答图②
当 时, 如答图(3),
作 轴于点, ,
解得 (不合题意, 舍去),
第3题答图③
第二章 一元二次方程
第10课 一元一次方程应用之动态面积问题
北师大版九年级上册
本套资料以教育部颁布的《数学课程标准(2022)版》为依据,结合新中考改革研究,立足北师大版本教材开发,通过课堂流程的优化设计,内容的层次设计,循序渐进,让不同层次的学生都学有所问,问有所探,探有所获,能力都有不同层次的提高,思维不断生长。
新授课通过激活思维、探究新知、双基巩固、综合运用、分层反馈等环节来完成。
资料简介
【探究1】若线段AB上有一点P,当PA=PB时,则称点P为线段AB的中点.如图2-10-1,已知数轴上A,B两点对应数分别为a和b,(a+2)2+|b-4|=0,P为数轴上一动点,对应数为x
【问题1】a=%/// /%,b=%// //%;
-2
A
4
B
探究1图
-2
4
解析:
因为(a+2)2+|b-4|=0,所以a=-2,b=4.
故答案为-2、4.
【问题2】若点P为线段AB的中点,
则P点对应的数x为%// //%.
若B为线段AP的中点时则P点对应的数x为%// //%.
1
10
解析:
若点P为线段AB的中点,则P点对应的数x为1.
若B为线段AP的中点时,AB=BP=6,
则P点对应的数x为10.
故答案为1、10.
【问题3】若点A、点B同时向左运动,它们的速度都为1个单位长度/秒,与此同时点P从-16处以2个单位长度/秒向右运动.
①设运动的时间为t秒,直接用含t的式子填空
AP= ;BP= .
|14-3t|
|20-3t|
②经过多长时间后,点A、点B、点P三点中其中一点是另外两点的中点?
解②t s后,点A的位置为:-2-t,
点B的位置为:4-t,点P的位置为:-16+2t.
当点A是PB的中点时,则-2-t-(-16+2t)=6,解得:t=;
当点P是AB的中点时,则-16+2t-(-2-t)=3,解得:t=;
当点B是PA的中点时,则-16+2t-(4-t)=6,解得:t=.
答:经过 s、 s、 s后,点A、点B、点P三点中其中一点是另外两点的中点.
C
Q
A
P
B
探究2图
【探究2】如图,在Rt△ABC中,∠C=90°,AC=30 cm,BC=25 cm,点P、Q分别从C、B点出发沿CA方向、BC方向匀速移动,速度分别是2 cm/s、1 cm/s,【问题1】经过t秒后点P,Q所走过的路程是%//// % ;%////% ;
PQ=%////% ;
2t cm
t cm
【问题2】求几秒后△PCQ的面积是△ACB面积的五分之二?
解(3)S△ACB=×AC×BC=×30×25=375,
∴S△ACB=×375=150.
又∵S△PCQ=×CQ×PC=×(25-t)×2t=25t-t2,
∴根据题意有:25t-t2=150,
∴化为一般式为t2-25t+150=0,解得t1=10,t2=15.
∴10秒或15秒后△PCQ的面积是△ACB面积的五分之二.
【问题3】利用方程解决此类实际问题的关键是?步骤是?
解:利用方程解决实际问题的关键是寻找等量关系. 步骤是:①审题;
②设未知数;
③利用等量关系列方程;
④解方程;
⑤检验;
⑥答.
1.如图,在Rt△ACB中,∠C=90°,点P,Q同时由A,B两点出发分别沿AC,BC方向向点C匀速移动(到点C为止),它们的速度都是1 m/s.经过几秒△PCQ的面积为Rt△ACB面积的一半?
C
P
Q
A
8m
B
6m
第1题图
解:设经过x秒后△PCQ的面积是Rt△ACB面积的一半,
则:(8-x)(6-x)=××6×8,
解得x1=12(不合题意,舍去),x2=2.
答:经2秒△PCQ的面积是Rt△ACB面积的一半.
2.(☆) 如图, 一次函数 的图像交 轴于点 , 交 轴于点 , 点 在线段 上(不与点 重合), 过点 分别作 和 的垂线, 垂足为 .
(1) 若点 的坐标为 , 那么
. (用含有 的代数 式表示)
(2) 在 (1) 的条件下, , (注意点 所在象限) . (用含 有 的代数式表示)
(3) 点 在何处时, 矩形 的面积为 1 请求出 的坐标.
第2题图
解: 由题意得 ,
整理得 , 解得 ,
故当 为 或 时, 矩形 的面积为 1 .
3.(☆) 如图, 由点 确定的 的面 积为 18 , 求 的值. 如果 呢
解 : 当 时, 如答图(1),
作 轴于点, ,
解得 .
第3题图
第3题答图①
当 时, 如答图 (2), 过点 作 轴于 .
解得 或 12 , 都不符合题意, 均舍去.
第3题答图②
当 时, 如答图(3),
作 轴于点, ,
解得 (不合题意, 舍去),
第3题答图③
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
