【五环分层导学-课件】3-3 用树状图或表格求概率3-北师大版数学九(上)
文档属性
| 名称 | 【五环分层导学-课件】3-3 用树状图或表格求概率3-北师大版数学九(上) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-30 17:15:02 | ||
图片预览








文档简介
(共20张PPT)
第三章 概率的进一步认识
第3课 用树状图或表格求概率(3)
北师大版九年级上册
本套资料以教育部颁布的《数学课程标准(2022)版》为依据,结合新中考改革研究,立足北师大版本教材开发,通过课堂流程的优化设计,内容的层次设计,循序渐进,让不同层次的学生都学有所问,问有所探,探有所获,能力都有不同层次的提高,思维不断生长。
新授课通过激活思维、探究新知、双基巩固、综合运用、分层反馈五个环节来完成。
资料简介
第一环节 激活思维 通过回顾与本节新知有关的旧知或熟悉的生活情境,唤醒、激活学生的旧知,为新知生成奠定基础,为知识的形成提供情境。
第二环节 探究新知 通过一系列问题,引领学生通过自主、合作、探究的方式,在解决问题串的过程中,生成新知,积累基本活动经验,提高分析问题和解决问题的能力。
第三环节 双基巩固 通过典型例题,及时巩固基础知识与基本技能,为学生初步应用新知解决问题积累经验。
第四环节 综合运用 以本节知识为核心,设计一道综合题,提高学生综合运用知识的能力,发散思维,渗透数学思想方法。
第五环节 分层反馈 通过由易到难的当堂练习或检测,及时反馈学生掌握情况,给教师课后针对辅导与布置课后作业的量和难度提供数据参考。
五环导学
(1)用列出表格的方法来分析和求解某些事件的概率的方法叫%// //%,用画树状图的方法列出某事件的所有可能的结果,求出其概率的方法叫%// //%.
(2)一个家庭有2个小孩.
①这个家庭有2个男孩的概率是%////%;
②这个家庭至少有1个女孩的概率是%////%.
(3)一个家庭有3个小孩.
①这个家庭有3个男孩的概率是%////%;
②这个家庭至少有1个女孩的概率是%////%.
列表法
树状图法
1
2
3
4
B
1
2
3
A
探究1图
【探究1】如图,转盘A的三个扇形面积相等,分别标有数字1,2,3,转盘B的四个扇形面积相等,分别有数字1,2,3,4.转动A、B转盘各一次,当转盘停止转动时,将指针所落扇形中的两个数字相乘(当指针落在四个扇形的交线上时,重新转动转盘).
(1)用树状图或列表法列出所有可能出现的结果;
(2)求两个数字的积为奇数的概率.
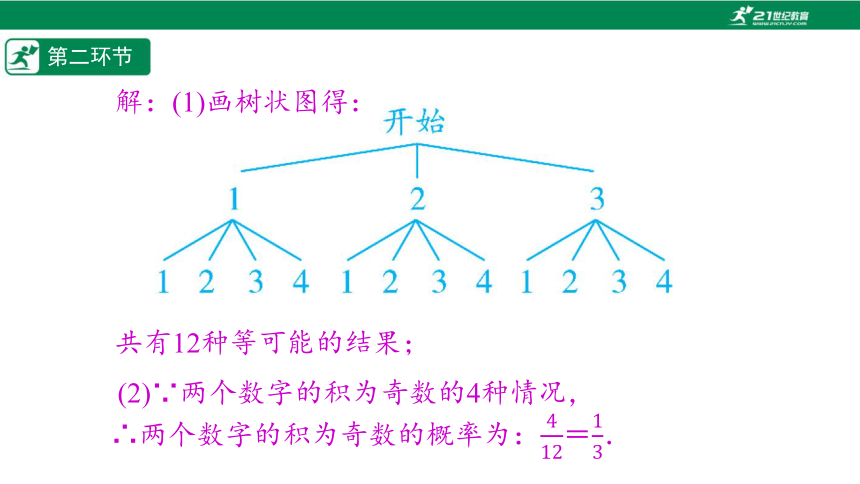
解:(1)画树状图得:
共有12种等可能的结果;
(2)∵两个数字的积为奇数的4种情况,
∴两个数字的积为奇数的概率为:=.
探究2图
红
白
A盘
黄
蓝
绿
B盘
【探究2】小明为学校联欢会设计了一个“配紫色”的游戏:如图是两个可以自由转动的转盘,每个转盘被分成面积相等的几个扇形,游戏者同时转动两个转盘,如果转盘A转出了红色,转盘B转出了蓝色,那么他就赢了,因为红色和蓝色在一起配成了紫色.
(1)利用树状图或列表的方
法表示游戏所有可能出现的结果.
(2)求出“配紫色”的概率.
解:(1)如答图
(2)P(配紫色)=.
【探究3】利用树状图或列表法求概率时需要注意些什么?
解:利用树状图或者列表法求概率时,要不重不漏地把所有可能的结果列出来.
【例题1】在一个不透明的布袋中装有相同的三个小球,其上面分别标注数字1、2、3,现从中任意摸出一个小球,将其上面的数字作为点M的横坐标;将球放回袋中搅匀,再从中任意摸出一个小球,将其上面的数字作为点M的纵坐标.
(1)写出点M坐标的所有可能的结果;
(2)求点M在直线y=x上的概率;
(3)求点M的横坐标与纵坐标之和是偶数的概率.
解:(1)∵列表得:
∴点M坐标的所有可能的结果有九个:(1,1)、(1,2)、(1,3)、(2,1)、(2,2)、(2,3)、(3,1)、(3,2)、(3,3).
(2)P(点M在直线y=x上)=P(点M的横、纵坐标相等)==.
(3)∵列表得:
∴P(点M的横坐标与纵坐标之和是偶数)=.
【例题 2 】(综合与实践) 某超市根据抽奖需要, 设计两个转盘进行“配紫色”抽奖游戏, 使得配 紫色的概率为三分之一, 请写出设计方案.
解: 两个转盘, 其中一个转盘被分成面积相等的红、蓝两部分,
另一个转盘被分成面积相等的红、 蓝、白三部分, 同时转动
两个转盘, 把转盘停止时指针所指的两种颜色进行配色, 求配
得紫色的 概率, 如答图 (1).针对该方案, 画树状图如答图(2),
共有 6 种等可能的结果,
其中配得紫色的结果数
为 2 , 所以配得紫色的概
率 , 符合题意.
1.小英和小丽用如图两个转盘做“配紫色”游戏,配成紫色小英得1分,否则小丽得1分,这个游戏对双方公平吗?说明理由.(红色+蓝色=紫色)
红
红
蓝
黄
红
蓝
黄
第1题图
解:这个游戏对双方是不公平的,理由如下:
列表得:
∵P(小英)=,P(小丽)=,∴ ≠ ,
∴这个游戏对双方是不公平的.
2.在一个不透明的口袋中装有4张相同的纸牌,它们分别标有数字1,2,3,4.随机地同时摸出两张牌.
(1)计算两张纸牌数字之和为5的概率;
(2)甲、乙两个人进行游戏,如果两张纸牌数字之和为奇数,则甲胜;如果两张纸牌数字之和为偶数,则乙胜.这个公平的游戏吗?请说明理由.若不公平,请问如何修改使得游戏公平?
解:根据题意,列表如下:
由上表可以看出,摸取一张纸牌然后放回,再随机摸取出纸牌,可能结果有16种,它们出现的可能性相等.
(1)两次摸取纸牌上数字之和为5(记为事件A)有4个,
P(A);
(2)这个游戏公平,理由如下:
∵两次摸出纸牌上数字之和为奇数(记为事件B)有8个,P(B),
两次摸出纸牌上数字之和为偶数(记为事件C)有8个,P(C),
∴两次摸出纸牌上数字之和为奇数和为偶数的概率相同,所以这个游戏公平.
3.(★)【中考真题】在一个不透明的布袋里装有4个标号为1、2、3、4的小球,它们的材质、形状、大小完全相同,小凯从布袋里随机取出一个小球,记下数字为x,小敏从剩下的3个小球中随机取出一个小球,记下数字为y,这样确定了点P的坐标(x,y).
(1)请你运用画树状图或列表的方法,写出点P所有可能的坐标;
(2)求点(x,y)在函数y=-x+5图象上的概率.
解:列表得:
(1)点P所有可能的坐标有:(1,2),(1,3),(1,4),(2,1),(2,3),(2,4),(3,1),(3,2),(3,4),(4,1),(4,2),(4,3)共12种;
(2)∵共有12种等可能的结果,其中在函数y=-x+5图象上的有4种,即:(1,4),(2,3),(3,2),(4,1).
∴点P(x,y)在函数y=-x+5图象上的概率为:P=.
第三章 概率的进一步认识
第3课 用树状图或表格求概率(3)
北师大版九年级上册
本套资料以教育部颁布的《数学课程标准(2022)版》为依据,结合新中考改革研究,立足北师大版本教材开发,通过课堂流程的优化设计,内容的层次设计,循序渐进,让不同层次的学生都学有所问,问有所探,探有所获,能力都有不同层次的提高,思维不断生长。
新授课通过激活思维、探究新知、双基巩固、综合运用、分层反馈五个环节来完成。
资料简介
第一环节 激活思维 通过回顾与本节新知有关的旧知或熟悉的生活情境,唤醒、激活学生的旧知,为新知生成奠定基础,为知识的形成提供情境。
第二环节 探究新知 通过一系列问题,引领学生通过自主、合作、探究的方式,在解决问题串的过程中,生成新知,积累基本活动经验,提高分析问题和解决问题的能力。
第三环节 双基巩固 通过典型例题,及时巩固基础知识与基本技能,为学生初步应用新知解决问题积累经验。
第四环节 综合运用 以本节知识为核心,设计一道综合题,提高学生综合运用知识的能力,发散思维,渗透数学思想方法。
第五环节 分层反馈 通过由易到难的当堂练习或检测,及时反馈学生掌握情况,给教师课后针对辅导与布置课后作业的量和难度提供数据参考。
五环导学
(1)用列出表格的方法来分析和求解某些事件的概率的方法叫%// //%,用画树状图的方法列出某事件的所有可能的结果,求出其概率的方法叫%// //%.
(2)一个家庭有2个小孩.
①这个家庭有2个男孩的概率是%////%;
②这个家庭至少有1个女孩的概率是%////%.
(3)一个家庭有3个小孩.
①这个家庭有3个男孩的概率是%////%;
②这个家庭至少有1个女孩的概率是%////%.
列表法
树状图法
1
2
3
4
B
1
2
3
A
探究1图
【探究1】如图,转盘A的三个扇形面积相等,分别标有数字1,2,3,转盘B的四个扇形面积相等,分别有数字1,2,3,4.转动A、B转盘各一次,当转盘停止转动时,将指针所落扇形中的两个数字相乘(当指针落在四个扇形的交线上时,重新转动转盘).
(1)用树状图或列表法列出所有可能出现的结果;
(2)求两个数字的积为奇数的概率.
解:(1)画树状图得:
共有12种等可能的结果;
(2)∵两个数字的积为奇数的4种情况,
∴两个数字的积为奇数的概率为:=.
探究2图
红
白
A盘
黄
蓝
绿
B盘
【探究2】小明为学校联欢会设计了一个“配紫色”的游戏:如图是两个可以自由转动的转盘,每个转盘被分成面积相等的几个扇形,游戏者同时转动两个转盘,如果转盘A转出了红色,转盘B转出了蓝色,那么他就赢了,因为红色和蓝色在一起配成了紫色.
(1)利用树状图或列表的方
法表示游戏所有可能出现的结果.
(2)求出“配紫色”的概率.
解:(1)如答图
(2)P(配紫色)=.
【探究3】利用树状图或列表法求概率时需要注意些什么?
解:利用树状图或者列表法求概率时,要不重不漏地把所有可能的结果列出来.
【例题1】在一个不透明的布袋中装有相同的三个小球,其上面分别标注数字1、2、3,现从中任意摸出一个小球,将其上面的数字作为点M的横坐标;将球放回袋中搅匀,再从中任意摸出一个小球,将其上面的数字作为点M的纵坐标.
(1)写出点M坐标的所有可能的结果;
(2)求点M在直线y=x上的概率;
(3)求点M的横坐标与纵坐标之和是偶数的概率.
解:(1)∵列表得:
∴点M坐标的所有可能的结果有九个:(1,1)、(1,2)、(1,3)、(2,1)、(2,2)、(2,3)、(3,1)、(3,2)、(3,3).
(2)P(点M在直线y=x上)=P(点M的横、纵坐标相等)==.
(3)∵列表得:
∴P(点M的横坐标与纵坐标之和是偶数)=.
【例题 2 】(综合与实践) 某超市根据抽奖需要, 设计两个转盘进行“配紫色”抽奖游戏, 使得配 紫色的概率为三分之一, 请写出设计方案.
解: 两个转盘, 其中一个转盘被分成面积相等的红、蓝两部分,
另一个转盘被分成面积相等的红、 蓝、白三部分, 同时转动
两个转盘, 把转盘停止时指针所指的两种颜色进行配色, 求配
得紫色的 概率, 如答图 (1).针对该方案, 画树状图如答图(2),
共有 6 种等可能的结果,
其中配得紫色的结果数
为 2 , 所以配得紫色的概
率 , 符合题意.
1.小英和小丽用如图两个转盘做“配紫色”游戏,配成紫色小英得1分,否则小丽得1分,这个游戏对双方公平吗?说明理由.(红色+蓝色=紫色)
红
红
蓝
黄
红
蓝
黄
第1题图
解:这个游戏对双方是不公平的,理由如下:
列表得:
∵P(小英)=,P(小丽)=,∴ ≠ ,
∴这个游戏对双方是不公平的.
2.在一个不透明的口袋中装有4张相同的纸牌,它们分别标有数字1,2,3,4.随机地同时摸出两张牌.
(1)计算两张纸牌数字之和为5的概率;
(2)甲、乙两个人进行游戏,如果两张纸牌数字之和为奇数,则甲胜;如果两张纸牌数字之和为偶数,则乙胜.这个公平的游戏吗?请说明理由.若不公平,请问如何修改使得游戏公平?
解:根据题意,列表如下:
由上表可以看出,摸取一张纸牌然后放回,再随机摸取出纸牌,可能结果有16种,它们出现的可能性相等.
(1)两次摸取纸牌上数字之和为5(记为事件A)有4个,
P(A);
(2)这个游戏公平,理由如下:
∵两次摸出纸牌上数字之和为奇数(记为事件B)有8个,P(B),
两次摸出纸牌上数字之和为偶数(记为事件C)有8个,P(C),
∴两次摸出纸牌上数字之和为奇数和为偶数的概率相同,所以这个游戏公平.
3.(★)【中考真题】在一个不透明的布袋里装有4个标号为1、2、3、4的小球,它们的材质、形状、大小完全相同,小凯从布袋里随机取出一个小球,记下数字为x,小敏从剩下的3个小球中随机取出一个小球,记下数字为y,这样确定了点P的坐标(x,y).
(1)请你运用画树状图或列表的方法,写出点P所有可能的坐标;
(2)求点(x,y)在函数y=-x+5图象上的概率.
解:列表得:
(1)点P所有可能的坐标有:(1,2),(1,3),(1,4),(2,1),(2,3),(2,4),(3,1),(3,2),(3,4),(4,1),(4,2),(4,3)共12种;
(2)∵共有12种等可能的结果,其中在函数y=-x+5图象上的有4种,即:(1,4),(2,3),(3,2),(4,1).
∴点P(x,y)在函数y=-x+5图象上的概率为:P=.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
