【五环分层导学-课件】4-8 黄金分割及其应用-北师大版数学九(上)
文档属性
| 名称 | 【五环分层导学-课件】4-8 黄金分割及其应用-北师大版数学九(上) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-30 17:15:02 | ||
图片预览






文档简介
(共16张PPT)
第四章 图形的相似
第8课 黄金分割及其应用
北师大版九年级上册
本套资料以教育部颁布的《数学课程标准(2022)版》为依据,结合新中考改革研究,立足北师大版本教材开发,通过课堂流程的优化设计,内容的层次设计,循序渐进,让不同层次的学生都学有所问,问有所探,探有所获,能力都有不同层次的提高,思维不断生长。
新授课通过激活思维、探究新知、双基巩固、综合运用、分层反馈五个环节来完成。
资料简介
第一环节 激活思维 通过回顾与本节新知有关的旧知或熟悉的生活情境,唤醒、激活学生的旧知,为新知生成奠定基础,为知识的形成提供情境。
第二环节 探究新知 通过一系列问题,引领学生通过自主、合作、探究的方式,在解决问题串的过程中,生成新知,积累基本活动经验,提高分析问题和解决问题的能力。
第三环节 双基巩固 通过典型例题,及时巩固基础知识与基本技能,为学生初步应用新知解决问题积累经验。
第四环节 综合运用 以本节知识为核心,设计一道综合题,提高学生综合运用知识的能力,发散思维,渗透数学思想方法。
第五环节 分层反馈 通过由易到难的当堂练习或检测,及时反馈学生掌握情况,给教师课后针对辅导与布置课后作业的量和难度提供数据参考。
五环导学
关于黄金分割比的起源大多数人认为来自毕达哥拉斯,据说在古希腊,有一天毕达哥拉斯走在街上,在经过铁匠铺前他听到铁匠打铁的声音非常好听,于是驻足倾听.他发现铁匠打铁的节奏很有规律,这个声音的比被毕达哥拉斯用数理的方式表达出来,被应用在很多领域.后来很多人专门研究过,开普勒称其为“神圣分割”,也有人称其为“金法”.在金字塔建成1000年后才出现毕达哥拉斯定律,可见这很早就存在.黄金分割比的作用不仅仅体现在诸如绘画、雕塑、音乐、建筑等艺术领域,而且在管理、工程设计等方面也有着不可忽视的作用.在我们生活中比比皆是.
C
A
B
问题1图
【问题1】如图,在线段AB上,点C把线段AB分成两条线段AC和BC,如果=,那么称线段AB被点C%// //%分割,点C叫做线段AB的黄金分割点,AC与AB的比叫做%// //%.
黄金
黄金比
C
A
B
问题2图
【问题2】你能计算黄金比吗?
已知:如图,C为AB的一个黄金分割点.求的值.
解:由=,得AC2=AB·BC.
设AB=1,AC=x,则BC=1-x,
∴x2=1×(1-x),即x2+x-1=0,
解得x1=,x2=(不合题意,舍去).
∴黄金比=≈0.618.
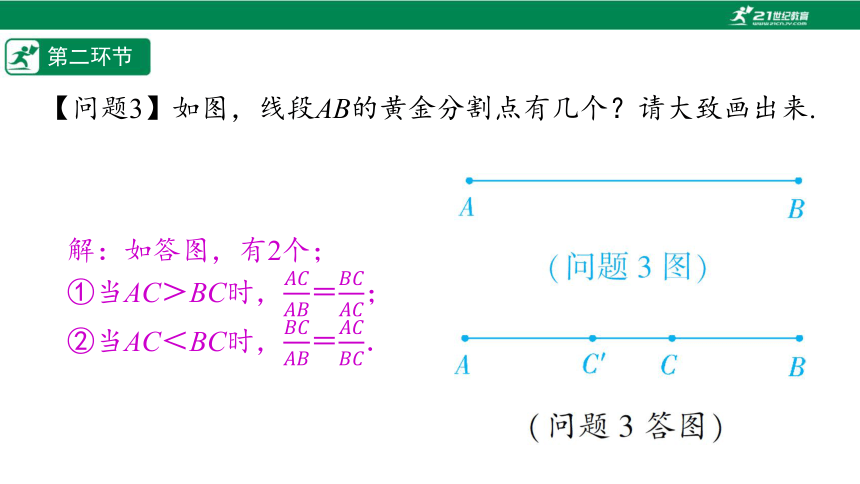
【问题3】如图,线段AB的黄金分割点有几个?请大致画出来.
解:如答图,有2个;
①当AC>BC时,=;
②当AC<BC时,=.
C
A
B
D
例题1图
【例题1】(1)如图,已知点C,D都是线段AB的黄金分割点,如果AB=10.那么AD=%// //%,BD=%// //%,CD=%/ ///%.
5-5
15-5
10-20
(2) 已知点 是线段 的黄金分割点, ,则
或
【例题2】 如图所示的是矩形 , 以矩形 的宽为边在其内部作正方形 , 那么我们 可以惊奇地发现 . 点 是 的黄金分割点吗 矩形的宽与长的比是黄金比吗
解: 四边形 为正方形,
四边形 为矩形,
,
点 是 的黄金分割点,
矩形的宽与长的比是黄金比.
A
C
B
第1题图
1.如图所示,点C把线段AB分成两条线段AC和BC,如果=,那么下列说法错误的是 (%// //%)
A.线段AB被点C黄金分割
B.点C叫做线段AB的黄金分割点
C.AB与AC的比叫做黄金比
D.AC与AB的比叫做黄金比
C
A
P
B
第2题图
2.如图,如果点P是线段AB的黄金分割点,且AP>PB,则下列命题:
①AB2=AP·PB,②BP2=AP·AB,③AP2=PB·AB,
④AP∶AB=PB∶AP,
其中正确的是%// //% .
③④
x
l
第3题图
3.(★)【中考真题】美是一种感觉,当人体下半身长与身高的比值越接近0.618时,越给人一种美感.如图,某女士身高165 cm,下半身长x与身高l的比值是0.60,为尽可能达到好的效果,她应穿的高跟鞋的高度大约为(精确到1 cm) (%// /%)
A.4 cm B.6 cm
C.8 cm D.10 cm
C
C
A
D
B
E
第4题图
4.如图,已知线段AB长为2,经过点B作BD⊥AB,使BD=AB,连接DA,在DA上截取DE=DB;在AB上截取AC=AE.则AC的长为%// //%.
-1
C
A
D
B
第5题图
5.(☆)如图,在黄金三角形ABC中,AB=AC=1,∠A=36°,BD平分∠ABC交AC于点D .
(1)求证:点D是线段AC的黄金分割点;
(2)求线段AD的长.
(1)证明:∵AB=AC=1,
∴∠ABC=∠C=(180°-∠A)=(180°-36°)=72°,
∵BD平分∠ABC交AC于点D,
∴∠ABD=∠CBD=∠ABC=36°,
∴∠BDC=180°-36°-72°=72°,
∴DA=DB,BD=BC,
∴AD=BD=BC,易得△BDC∽△ABC,
∴BC∶AC=CD∶BC,即BC2=CD·AC,
∴AD2=CD·AC,∴点D是线段AC的黄金分割点;
(2)解:设AD=x,则CD=AC-AD=1-x,
∵AD2=CD·AC,∴x2=1-x,
解得x1=,x2=(不合题意,舍去),
即AD的长为.
第四章 图形的相似
第8课 黄金分割及其应用
北师大版九年级上册
本套资料以教育部颁布的《数学课程标准(2022)版》为依据,结合新中考改革研究,立足北师大版本教材开发,通过课堂流程的优化设计,内容的层次设计,循序渐进,让不同层次的学生都学有所问,问有所探,探有所获,能力都有不同层次的提高,思维不断生长。
新授课通过激活思维、探究新知、双基巩固、综合运用、分层反馈五个环节来完成。
资料简介
第一环节 激活思维 通过回顾与本节新知有关的旧知或熟悉的生活情境,唤醒、激活学生的旧知,为新知生成奠定基础,为知识的形成提供情境。
第二环节 探究新知 通过一系列问题,引领学生通过自主、合作、探究的方式,在解决问题串的过程中,生成新知,积累基本活动经验,提高分析问题和解决问题的能力。
第三环节 双基巩固 通过典型例题,及时巩固基础知识与基本技能,为学生初步应用新知解决问题积累经验。
第四环节 综合运用 以本节知识为核心,设计一道综合题,提高学生综合运用知识的能力,发散思维,渗透数学思想方法。
第五环节 分层反馈 通过由易到难的当堂练习或检测,及时反馈学生掌握情况,给教师课后针对辅导与布置课后作业的量和难度提供数据参考。
五环导学
关于黄金分割比的起源大多数人认为来自毕达哥拉斯,据说在古希腊,有一天毕达哥拉斯走在街上,在经过铁匠铺前他听到铁匠打铁的声音非常好听,于是驻足倾听.他发现铁匠打铁的节奏很有规律,这个声音的比被毕达哥拉斯用数理的方式表达出来,被应用在很多领域.后来很多人专门研究过,开普勒称其为“神圣分割”,也有人称其为“金法”.在金字塔建成1000年后才出现毕达哥拉斯定律,可见这很早就存在.黄金分割比的作用不仅仅体现在诸如绘画、雕塑、音乐、建筑等艺术领域,而且在管理、工程设计等方面也有着不可忽视的作用.在我们生活中比比皆是.
C
A
B
问题1图
【问题1】如图,在线段AB上,点C把线段AB分成两条线段AC和BC,如果=,那么称线段AB被点C%// //%分割,点C叫做线段AB的黄金分割点,AC与AB的比叫做%// //%.
黄金
黄金比
C
A
B
问题2图
【问题2】你能计算黄金比吗?
已知:如图,C为AB的一个黄金分割点.求的值.
解:由=,得AC2=AB·BC.
设AB=1,AC=x,则BC=1-x,
∴x2=1×(1-x),即x2+x-1=0,
解得x1=,x2=(不合题意,舍去).
∴黄金比=≈0.618.
【问题3】如图,线段AB的黄金分割点有几个?请大致画出来.
解:如答图,有2个;
①当AC>BC时,=;
②当AC<BC时,=.
C
A
B
D
例题1图
【例题1】(1)如图,已知点C,D都是线段AB的黄金分割点,如果AB=10.那么AD=%// //%,BD=%// //%,CD=%/ ///%.
5-5
15-5
10-20
(2) 已知点 是线段 的黄金分割点, ,则
或
【例题2】 如图所示的是矩形 , 以矩形 的宽为边在其内部作正方形 , 那么我们 可以惊奇地发现 . 点 是 的黄金分割点吗 矩形的宽与长的比是黄金比吗
解: 四边形 为正方形,
四边形 为矩形,
,
点 是 的黄金分割点,
矩形的宽与长的比是黄金比.
A
C
B
第1题图
1.如图所示,点C把线段AB分成两条线段AC和BC,如果=,那么下列说法错误的是 (%// //%)
A.线段AB被点C黄金分割
B.点C叫做线段AB的黄金分割点
C.AB与AC的比叫做黄金比
D.AC与AB的比叫做黄金比
C
A
P
B
第2题图
2.如图,如果点P是线段AB的黄金分割点,且AP>PB,则下列命题:
①AB2=AP·PB,②BP2=AP·AB,③AP2=PB·AB,
④AP∶AB=PB∶AP,
其中正确的是%// //% .
③④
x
l
第3题图
3.(★)【中考真题】美是一种感觉,当人体下半身长与身高的比值越接近0.618时,越给人一种美感.如图,某女士身高165 cm,下半身长x与身高l的比值是0.60,为尽可能达到好的效果,她应穿的高跟鞋的高度大约为(精确到1 cm) (%// /%)
A.4 cm B.6 cm
C.8 cm D.10 cm
C
C
A
D
B
E
第4题图
4.如图,已知线段AB长为2,经过点B作BD⊥AB,使BD=AB,连接DA,在DA上截取DE=DB;在AB上截取AC=AE.则AC的长为%// //%.
-1
C
A
D
B
第5题图
5.(☆)如图,在黄金三角形ABC中,AB=AC=1,∠A=36°,BD平分∠ABC交AC于点D .
(1)求证:点D是线段AC的黄金分割点;
(2)求线段AD的长.
(1)证明:∵AB=AC=1,
∴∠ABC=∠C=(180°-∠A)=(180°-36°)=72°,
∵BD平分∠ABC交AC于点D,
∴∠ABD=∠CBD=∠ABC=36°,
∴∠BDC=180°-36°-72°=72°,
∴DA=DB,BD=BC,
∴AD=BD=BC,易得△BDC∽△ABC,
∴BC∶AC=CD∶BC,即BC2=CD·AC,
∴AD2=CD·AC,∴点D是线段AC的黄金分割点;
(2)解:设AD=x,则CD=AC-AD=1-x,
∵AD2=CD·AC,∴x2=1-x,
解得x1=,x2=(不合题意,舍去),
即AD的长为.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
