人教版八年级下册18.1.2 平行四边形的判定 同步练习(含答案)
文档属性
| 名称 | 人教版八年级下册18.1.2 平行四边形的判定 同步练习(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 219.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-31 00:00:00 | ||
图片预览



文档简介
第十八章 平行四边形
18.1 平行四边形
第2课时 平行四边形的判定
一、选择题
1.在四边形ABCD中,AB=CD,则下列条件能判定四边形ABCD为平行四边形的是( )
A.AD∥BC B.∠A+∠C=180° C.AB∥CD D.∠A+∠B=180°
2.下面给出了四边形ABCD中∠A,∠B,∠C,∠D的度数之比,其中能判定四边形ABCD是平行四边形的是( )
A.1∶2∶3∶4 B.2∶2∶3∶3 C.2∶3∶2∶3 D.2∶3∶3∶2
3.下列说法正确的是( )
A.对角线相等的四边形是平行四边形
B.对角线互相平分的四边形是平行四边形
C.对角线互相垂直的四边形是平行四边形
D.对角线互相垂直且相等的四边形是平行四边形
4.在四边形ABCD中,AB∥CD,AB=CD,若∠B=55°,则∠D的度数是( )
A.145° B.125° C.55° D.35°
5.在△ABC中,D,E分别是边AB,AC的中点,连接DE.若∠B=50°,则∠ADE=( )
A.40° B.50° C.90° D.130°
6.如图,在四边形ABCD中,对角线AC,BD相交于点O,下列条件不能判定这个四边形是平行四边形的是( )
A.AB∥DC,AD∥BC B.AB∥DC,∠DAB=∠DCB
C.AO=CO,AB=DC D.AB∥DC,DO=BO
7.如图,在△ABC中,AB=AC=8,点E,F,G分别在边AB,BC,AC上,EF∥AC,EF=AG,则四边形AEFG的周长是( )
A.8 B.16 C.24 D.32
8.如图,在四边形ABCD中,P,R分别是BC,DC上的点,E,F分别是AP,PR的中点.当点P在BC上从点B向点C移动,而点R不动时,线段EF的长( )
A.逐渐增大 B.逐渐减小 C.不变 D.不能确定
9.如图,在由25个点构成的5×5的正方形点阵中,横、纵方向相邻的两点之间的距离都是1个单位长度.定义:以点阵中的四个点为顶点的平行四边形叫做阵点平行四边形.图中以A,B为顶点,面积为4的阵点平行四边形的个数是( )
A.6 B.7 C.9 D.11
二、填空题
10.如图,D是直线l外一点,在l上取两点A,B,连接AD,分别以点B,D为圆心,AD,AB的长为半径画弧,两弧交于点C,连接CD,BC,则四边形ABCD是平行四边形.理是 .
11.如图,在四边形ABCD中,AO=OC,BD=12 cm,则当OB= cm时,四边形ABCD是平行四边形.
12.如图,在Rt△ABC中,∠B=90°,∠BAC=30°,AC=6,将△ABC沿BC向右平移得到△DEF.若四边形ACFD的面积等于6,则平移的距离为 .
13.在平面直角坐标系中,平行四边形的其中三个顶点的坐标分别为(0,0),(3,0),(4,2),则第四个顶点的坐标是 .
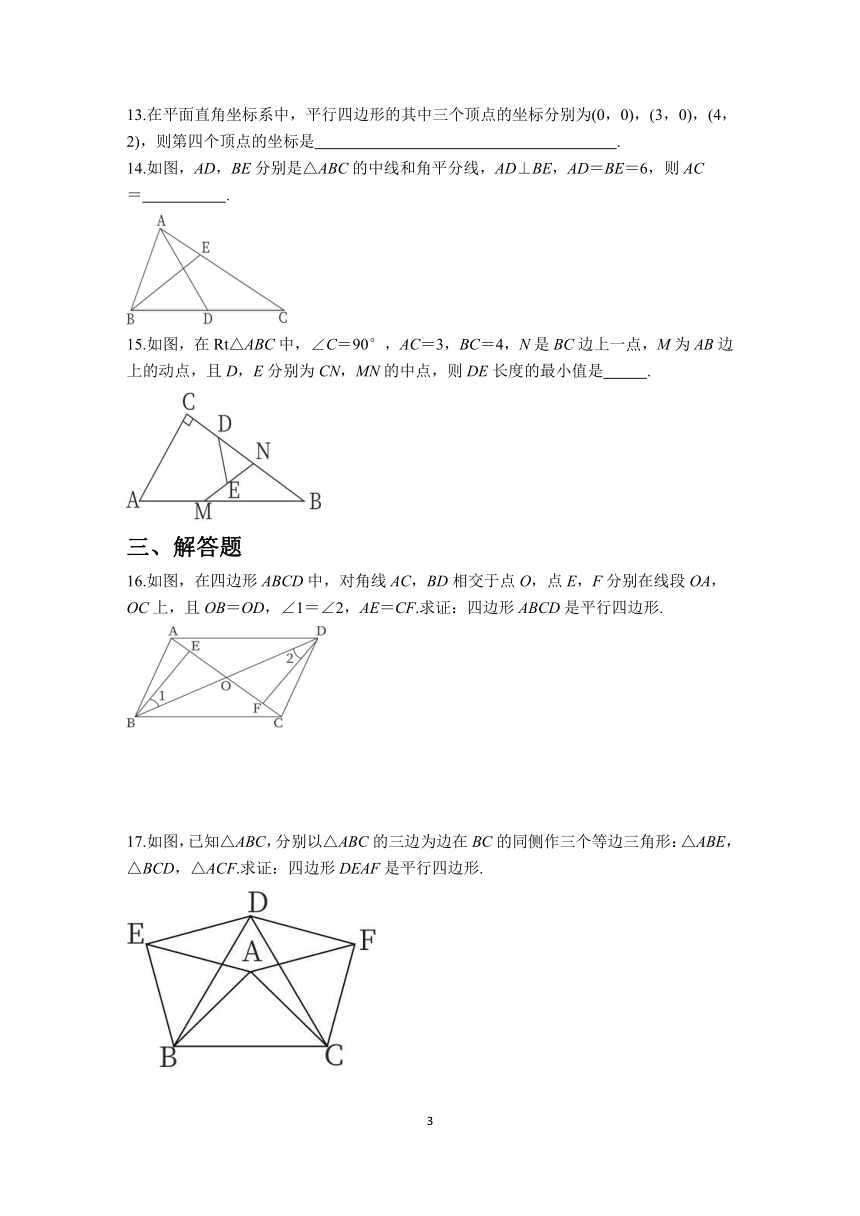
14.如图,AD,BE分别是△ABC的中线和角平分线,AD⊥BE,AD=BE=6,则AC= .
15.如图,在Rt△ABC中,∠C=90°,AC=3,BC=4,N是BC边上一点,M为AB边上的动点,且D,E分别为CN,MN的中点,则DE长度的最小值是 .
三、解答题
16.如图,在四边形ABCD中,对角线AC,BD相交于点O,点E,F分别在线段OA,OC上,且OB=OD,∠1=∠2,AE=CF.求证:四边形ABCD是平行四边形.
17.如图,已知△ABC,分别以△ABC的三边为边在BC的同侧作三个等边三角形:△ABE,△BCD,△ACF.求证:四边形DEAF是平行四边形.
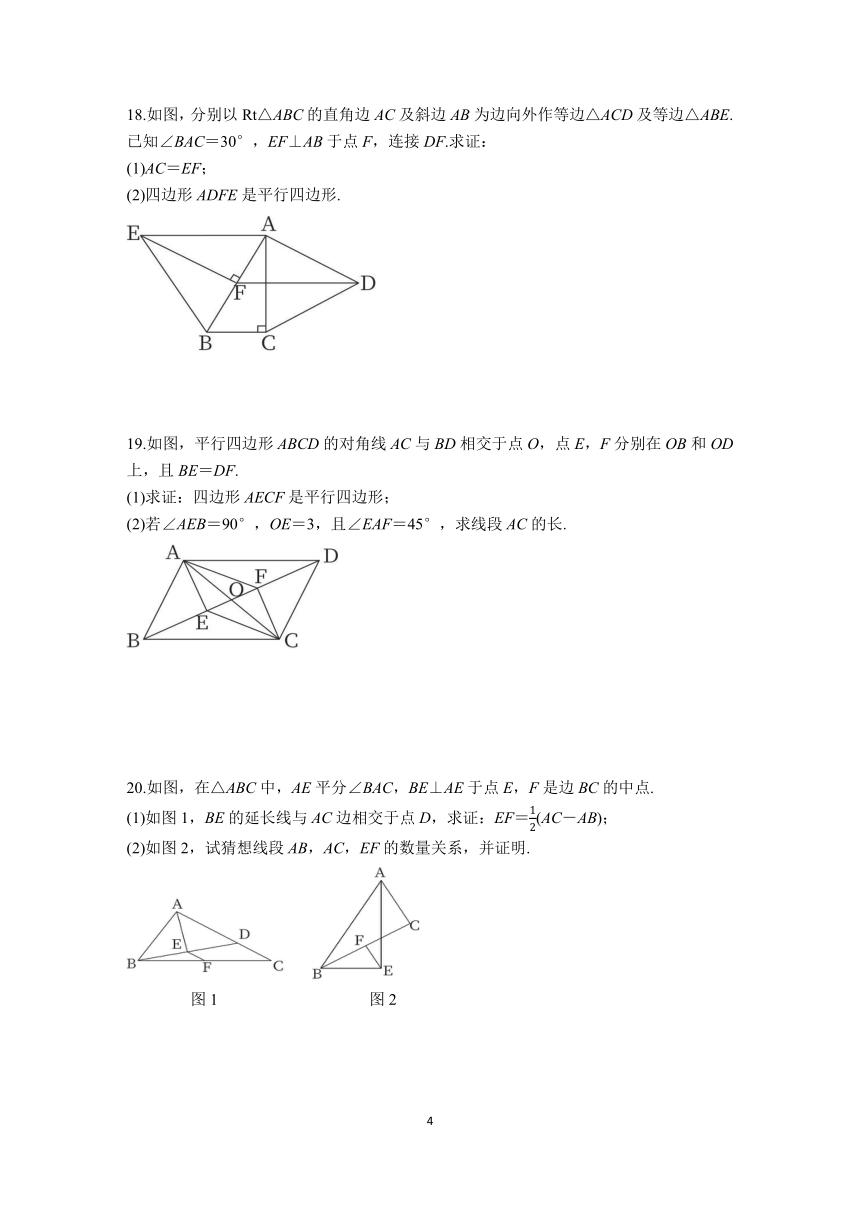
18.如图,分别以Rt△ABC的直角边AC及斜边AB为边向外作等边△ACD及等边△ABE.已知∠BAC=30°,EF⊥AB于点F,连接DF.求证:
(1)AC=EF;
(2)四边形ADFE是平行四边形.
19.如图,平行四边形ABCD的对角线AC与BD相交于点O,点E,F分别在OB和OD上,且BE=DF.
(1)求证:四边形AECF是平行四边形;
(2)若∠AEB=90°,OE=3,且∠EAF=45°,求线段AC的长.
20.如图,在△ABC中,AE平分∠BAC,BE⊥AE于点E,F是边BC的中点.
(1)如图1,BE的延长线与AC边相交于点D,求证:EF=(AC-AB);
(2)如图2,试猜想线段AB,AC,EF的数量关系,并证明.
图1 图2
21.选做题:请在A,B两题中任选一题作答.
A:如图,在△ABC中,AB=AC=20 cm,BD⊥AC于点D,且BD=16 cm.点M从点A出发,沿AC方向匀速运动,速度为4 cm/s;同时点P由点B出发,沿BA方向匀速运动,速度为1 cm/s,过点P的直线PQ∥AC,交BC于点Q,连接PM,设运动时间为t s(0<t<5).当t为何值时,以P,Q,D,M为顶点的四边形是平行四边形?
B:如图,在四边形ABCD中,AB∥CD,AB=24 cm,DC=10 cm,点P自点D向点C以1 cm/s的速度运动,到点C停止.点Q自点B向点A以3 cm/s的速度运动,到点A停止,点P,Q同时出发.试求经过多长时间后,P,Q两点和四边形ABCD的两个顶点所形成的四边形是平行四边形.我选做 题(填A或B),并写出完整的答题过程.
1
参考答案
一、选择题
1.在四边形ABCD中,AB=CD,则下列条件能判定四边形ABCD为平行四边形的是( C )
A.AD∥BC B.∠A+∠C=180° C.AB∥CD D.∠A+∠B=180°
2.下面给出了四边形ABCD中∠A,∠B,∠C,∠D的度数之比,其中能判定四边形ABCD是平行四边形的是( C )
A.1∶2∶3∶4 B.2∶2∶3∶3 C.2∶3∶2∶3 D.2∶3∶3∶2
3.下列说法正确的是( B )
A.对角线相等的四边形是平行四边形
B.对角线互相平分的四边形是平行四边形
C.对角线互相垂直的四边形是平行四边形
D.对角线互相垂直且相等的四边形是平行四边形
4.在四边形ABCD中,AB∥CD,AB=CD,若∠B=55°,则∠D的度数是( C )
A.145° B.125° C.55° D.35°
5.在△ABC中,D,E分别是边AB,AC的中点,连接DE.若∠B=50°,则∠ADE=( B )
A.40° B.50° C.90° D.130°
6.如图,在四边形ABCD中,对角线AC,BD相交于点O,下列条件不能判定这个四边形是平行四边形的是( C )
A.AB∥DC,AD∥BC B.AB∥DC,∠DAB=∠DCB
C.AO=CO,AB=DC D.AB∥DC,DO=BO
7.如图,在△ABC中,AB=AC=8,点E,F,G分别在边AB,BC,AC上,EF∥AC,EF=AG,则四边形AEFG的周长是( B )
A.8 B.16 C.24 D.32
8.如图,在四边形ABCD中,P,R分别是BC,DC上的点,E,F分别是AP,PR的中点.当点P在BC上从点B向点C移动,而点R不动时,线段EF的长( C )
A.逐渐增大 B.逐渐减小 C.不变 D.不能确定
9.如图,在由25个点构成的5×5的正方形点阵中,横、纵方向相邻的两点之间的距离都是1个单位长度.定义:以点阵中的四个点为顶点的平行四边形叫做阵点平行四边形.图中以A,B为顶点,面积为4的阵点平行四边形的个数是( D )
A.6 B.7 C.9 D.11
二、填空题
10.如图,D是直线l外一点,在l上取两点A,B,连接AD,分别以点B,D为圆心,AD,AB的长为半径画弧,两弧交于点C,连接CD,BC,则四边形ABCD是平行四边形.理是 .
【答案】两组对边分别相等的四边形是平行四边形
11.如图,在四边形ABCD中,AO=OC,BD=12 cm,则当OB= cm时,四边形ABCD是平行四边形.
【答案】6
12.如图,在Rt△ABC中,∠B=90°,∠BAC=30°,AC=6,将△ABC沿BC向右平移得到△DEF.若四边形ACFD的面积等于6,则平移的距离为 .
【答案】2
13.在平面直角坐标系中,平行四边形的其中三个顶点的坐标分别为(0,0),(3,0),(4,2),则第四个顶点的坐标是 .
【答案】(1,2)或(7,2)或(-1,-2)
14.如图,AD,BE分别是△ABC的中线和角平分线,AD⊥BE,AD=BE=6,则AC= .
【答案】
提示:取CE中点F,连接DF.
15.如图,在Rt△ABC中,∠C=90°,AC=3,BC=4,N是BC边上一点,M为AB边上的动点,且D,E分别为CN,MN的中点,则DE长度的最小值是 .
【答案】
三、解答题
16.如图,在四边形ABCD中,对角线AC,BD相交于点O,点E,F分别在线段OA,OC上,且OB=OD,∠1=∠2,AE=CF.求证:四边形ABCD是平行四边形.
证明:易证△BEO≌△DFO,∴OE=OF.
∵AE=CF,∴OA=OC.
∵OB=OD,∴四边形ABCD是平行四边形.
17.如图,已知△ABC,分别以△ABC的三边为边在BC的同侧作三个等边三角形:△ABE,△BCD,△ACF.求证:四边形DEAF是平行四边形.
证明:∵△ABE,△BCD都是等边三角形,
∴BE=AB,BD=BC,∠EBA=∠DBC=60°,
∴∠DBE=60°-∠DBA,∠ABC=60°-∠DBA,
∴∠DBE=∠CBA.
易证△DBE≌△CBA,∴DE=AC.
又∵△ACF是等边三角形,
∴AC=AF,∴DE=AF.
同理可得△CBA≌△CDF,∴DF=AB=AE.
∵DE=AF,AE=DF,
∴四边形DEAF是平行四边形.
18.如图,分别以Rt△ABC的直角边AC及斜边AB为边向外作等边△ACD及等边△ABE.已知∠BAC=30°,EF⊥AB于点F,连接DF.求证:
(1)AC=EF;
(2)四边形ADFE是平行四边形.
证明:(1)∵△ABE是等边三角形,EF⊥AB,
∴∠AEF=∠AEB=30°,AE=AB,∠EFA=90°.
易证△AEF≌△BAC,∴AC=EF.
(2)∵△ACD是等边三角形,
∴AC=AD,∠DAC=60°.
由(1)知AC=EF,∴AD=EF.
∵∠BAC=30°,∴∠FAD=∠BAC+∠DAC=90°.
∵∠EFA=90°,∴AD∥EF,
∴四边形ADFE是平行四边形.
19.如图,平行四边形ABCD的对角线AC与BD相交于点O,点E,F分别在OB和OD上,且BE=DF.
(1)求证:四边形AECF是平行四边形;
(2)若∠AEB=90°,OE=3,且∠EAF=45°,求线段AC的长.
解:(1)∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD.
∵BE=DF,∴OB-BE=OD-DF,即OE=OF.
又∵OA=OC,
∴四边形AECF是平行四边形.
(2)由(1)知OF=OE=3,OA=OC.
∵∠AEB=90°,∠EAF=45°,
∴EA=EF=2OE=6,
∴OA==3,
∴AC=2OA=6.
20.如图,在△ABC中,AE平分∠BAC,BE⊥AE于点E,F是边BC的中点.
(1)如图1,BE的延长线与AC边相交于点D,求证:EF=(AC-AB);
(2)如图2,试猜想线段AB,AC,EF的数量关系,并证明.
图1 图2
解:(1)∵AE⊥BD,∴∠AED=∠AEB=90°.
∵AE平分∠BAC,∴∠BAE=∠DAE,
∴∠ABE=∠ADE,∴AB=AD.
∵AE⊥BD,∴BE=DE.
∵BF=FC,
∴EF=(AC-AD)=(AC-AB).
(2)EF=(AB-AC). 证明:延长AC,BE交于点D(过程略).
21.选做题:请在A,B两题中任选一题作答.
A:如图,在△ABC中,AB=AC=20 cm,BD⊥AC于点D,且BD=16 cm.点M从点A出发,沿AC方向匀速运动,速度为4 cm/s;同时点P由点B出发,沿BA方向匀速运动,速度为1 cm/s,过点P的直线PQ∥AC,交BC于点Q,连接PM,设运动时间为t s(0<t<5).当t为何值时,以P,Q,D,M为顶点的四边形是平行四边形?
B:如图,在四边形ABCD中,AB∥CD,AB=24 cm,DC=10 cm,点P自点D向点C以1 cm/s的速度运动,到点C停止.点Q自点B向点A以3 cm/s的速度运动,到点A停止,点P,Q同时出发.试求经过多长时间后,P,Q两点和四边形ABCD的两个顶点所形成的四边形是平行四边形.我选做 题(填A或B),并写出完整的答题过程.
A:解:当t=或t=4时,以P,Q,D,M为顶点的四边形是平行四边形.
B:解:①设经过x s后,四边形PQAD是平行四边形.
根据题意,得x=24-3x,解得x=6,
∴经过6 s后,四边形PQAD是平行四边形.
②设经过y s后,四边形PQBC是平行四边形.
根据题意,得10-y=3y,解得y=2.5,
∴经过2.5 s后,四边形PQBC是平行四边形.
③设经过z s后,四边形PAQC是平行四边形.
根据题意,得10-z=24-3z,解得z=7,
∴经过7 s后,四边形PAQC是平行四边形.
综上所述,经过2.5 s或6 s或7 s后,P,Q两点和梯形ABCD的两个顶点所形成的四边形是平行四边形.
18.1 平行四边形
第2课时 平行四边形的判定
一、选择题
1.在四边形ABCD中,AB=CD,则下列条件能判定四边形ABCD为平行四边形的是( )
A.AD∥BC B.∠A+∠C=180° C.AB∥CD D.∠A+∠B=180°
2.下面给出了四边形ABCD中∠A,∠B,∠C,∠D的度数之比,其中能判定四边形ABCD是平行四边形的是( )
A.1∶2∶3∶4 B.2∶2∶3∶3 C.2∶3∶2∶3 D.2∶3∶3∶2
3.下列说法正确的是( )
A.对角线相等的四边形是平行四边形
B.对角线互相平分的四边形是平行四边形
C.对角线互相垂直的四边形是平行四边形
D.对角线互相垂直且相等的四边形是平行四边形
4.在四边形ABCD中,AB∥CD,AB=CD,若∠B=55°,则∠D的度数是( )
A.145° B.125° C.55° D.35°
5.在△ABC中,D,E分别是边AB,AC的中点,连接DE.若∠B=50°,则∠ADE=( )
A.40° B.50° C.90° D.130°
6.如图,在四边形ABCD中,对角线AC,BD相交于点O,下列条件不能判定这个四边形是平行四边形的是( )
A.AB∥DC,AD∥BC B.AB∥DC,∠DAB=∠DCB
C.AO=CO,AB=DC D.AB∥DC,DO=BO
7.如图,在△ABC中,AB=AC=8,点E,F,G分别在边AB,BC,AC上,EF∥AC,EF=AG,则四边形AEFG的周长是( )
A.8 B.16 C.24 D.32
8.如图,在四边形ABCD中,P,R分别是BC,DC上的点,E,F分别是AP,PR的中点.当点P在BC上从点B向点C移动,而点R不动时,线段EF的长( )
A.逐渐增大 B.逐渐减小 C.不变 D.不能确定
9.如图,在由25个点构成的5×5的正方形点阵中,横、纵方向相邻的两点之间的距离都是1个单位长度.定义:以点阵中的四个点为顶点的平行四边形叫做阵点平行四边形.图中以A,B为顶点,面积为4的阵点平行四边形的个数是( )
A.6 B.7 C.9 D.11
二、填空题
10.如图,D是直线l外一点,在l上取两点A,B,连接AD,分别以点B,D为圆心,AD,AB的长为半径画弧,两弧交于点C,连接CD,BC,则四边形ABCD是平行四边形.理是 .
11.如图,在四边形ABCD中,AO=OC,BD=12 cm,则当OB= cm时,四边形ABCD是平行四边形.
12.如图,在Rt△ABC中,∠B=90°,∠BAC=30°,AC=6,将△ABC沿BC向右平移得到△DEF.若四边形ACFD的面积等于6,则平移的距离为 .
13.在平面直角坐标系中,平行四边形的其中三个顶点的坐标分别为(0,0),(3,0),(4,2),则第四个顶点的坐标是 .
14.如图,AD,BE分别是△ABC的中线和角平分线,AD⊥BE,AD=BE=6,则AC= .
15.如图,在Rt△ABC中,∠C=90°,AC=3,BC=4,N是BC边上一点,M为AB边上的动点,且D,E分别为CN,MN的中点,则DE长度的最小值是 .
三、解答题
16.如图,在四边形ABCD中,对角线AC,BD相交于点O,点E,F分别在线段OA,OC上,且OB=OD,∠1=∠2,AE=CF.求证:四边形ABCD是平行四边形.
17.如图,已知△ABC,分别以△ABC的三边为边在BC的同侧作三个等边三角形:△ABE,△BCD,△ACF.求证:四边形DEAF是平行四边形.
18.如图,分别以Rt△ABC的直角边AC及斜边AB为边向外作等边△ACD及等边△ABE.已知∠BAC=30°,EF⊥AB于点F,连接DF.求证:
(1)AC=EF;
(2)四边形ADFE是平行四边形.
19.如图,平行四边形ABCD的对角线AC与BD相交于点O,点E,F分别在OB和OD上,且BE=DF.
(1)求证:四边形AECF是平行四边形;
(2)若∠AEB=90°,OE=3,且∠EAF=45°,求线段AC的长.
20.如图,在△ABC中,AE平分∠BAC,BE⊥AE于点E,F是边BC的中点.
(1)如图1,BE的延长线与AC边相交于点D,求证:EF=(AC-AB);
(2)如图2,试猜想线段AB,AC,EF的数量关系,并证明.
图1 图2
21.选做题:请在A,B两题中任选一题作答.
A:如图,在△ABC中,AB=AC=20 cm,BD⊥AC于点D,且BD=16 cm.点M从点A出发,沿AC方向匀速运动,速度为4 cm/s;同时点P由点B出发,沿BA方向匀速运动,速度为1 cm/s,过点P的直线PQ∥AC,交BC于点Q,连接PM,设运动时间为t s(0<t<5).当t为何值时,以P,Q,D,M为顶点的四边形是平行四边形?
B:如图,在四边形ABCD中,AB∥CD,AB=24 cm,DC=10 cm,点P自点D向点C以1 cm/s的速度运动,到点C停止.点Q自点B向点A以3 cm/s的速度运动,到点A停止,点P,Q同时出发.试求经过多长时间后,P,Q两点和四边形ABCD的两个顶点所形成的四边形是平行四边形.我选做 题(填A或B),并写出完整的答题过程.
1
参考答案
一、选择题
1.在四边形ABCD中,AB=CD,则下列条件能判定四边形ABCD为平行四边形的是( C )
A.AD∥BC B.∠A+∠C=180° C.AB∥CD D.∠A+∠B=180°
2.下面给出了四边形ABCD中∠A,∠B,∠C,∠D的度数之比,其中能判定四边形ABCD是平行四边形的是( C )
A.1∶2∶3∶4 B.2∶2∶3∶3 C.2∶3∶2∶3 D.2∶3∶3∶2
3.下列说法正确的是( B )
A.对角线相等的四边形是平行四边形
B.对角线互相平分的四边形是平行四边形
C.对角线互相垂直的四边形是平行四边形
D.对角线互相垂直且相等的四边形是平行四边形
4.在四边形ABCD中,AB∥CD,AB=CD,若∠B=55°,则∠D的度数是( C )
A.145° B.125° C.55° D.35°
5.在△ABC中,D,E分别是边AB,AC的中点,连接DE.若∠B=50°,则∠ADE=( B )
A.40° B.50° C.90° D.130°
6.如图,在四边形ABCD中,对角线AC,BD相交于点O,下列条件不能判定这个四边形是平行四边形的是( C )
A.AB∥DC,AD∥BC B.AB∥DC,∠DAB=∠DCB
C.AO=CO,AB=DC D.AB∥DC,DO=BO
7.如图,在△ABC中,AB=AC=8,点E,F,G分别在边AB,BC,AC上,EF∥AC,EF=AG,则四边形AEFG的周长是( B )
A.8 B.16 C.24 D.32
8.如图,在四边形ABCD中,P,R分别是BC,DC上的点,E,F分别是AP,PR的中点.当点P在BC上从点B向点C移动,而点R不动时,线段EF的长( C )
A.逐渐增大 B.逐渐减小 C.不变 D.不能确定
9.如图,在由25个点构成的5×5的正方形点阵中,横、纵方向相邻的两点之间的距离都是1个单位长度.定义:以点阵中的四个点为顶点的平行四边形叫做阵点平行四边形.图中以A,B为顶点,面积为4的阵点平行四边形的个数是( D )
A.6 B.7 C.9 D.11
二、填空题
10.如图,D是直线l外一点,在l上取两点A,B,连接AD,分别以点B,D为圆心,AD,AB的长为半径画弧,两弧交于点C,连接CD,BC,则四边形ABCD是平行四边形.理是 .
【答案】两组对边分别相等的四边形是平行四边形
11.如图,在四边形ABCD中,AO=OC,BD=12 cm,则当OB= cm时,四边形ABCD是平行四边形.
【答案】6
12.如图,在Rt△ABC中,∠B=90°,∠BAC=30°,AC=6,将△ABC沿BC向右平移得到△DEF.若四边形ACFD的面积等于6,则平移的距离为 .
【答案】2
13.在平面直角坐标系中,平行四边形的其中三个顶点的坐标分别为(0,0),(3,0),(4,2),则第四个顶点的坐标是 .
【答案】(1,2)或(7,2)或(-1,-2)
14.如图,AD,BE分别是△ABC的中线和角平分线,AD⊥BE,AD=BE=6,则AC= .
【答案】
提示:取CE中点F,连接DF.
15.如图,在Rt△ABC中,∠C=90°,AC=3,BC=4,N是BC边上一点,M为AB边上的动点,且D,E分别为CN,MN的中点,则DE长度的最小值是 .
【答案】
三、解答题
16.如图,在四边形ABCD中,对角线AC,BD相交于点O,点E,F分别在线段OA,OC上,且OB=OD,∠1=∠2,AE=CF.求证:四边形ABCD是平行四边形.
证明:易证△BEO≌△DFO,∴OE=OF.
∵AE=CF,∴OA=OC.
∵OB=OD,∴四边形ABCD是平行四边形.
17.如图,已知△ABC,分别以△ABC的三边为边在BC的同侧作三个等边三角形:△ABE,△BCD,△ACF.求证:四边形DEAF是平行四边形.
证明:∵△ABE,△BCD都是等边三角形,
∴BE=AB,BD=BC,∠EBA=∠DBC=60°,
∴∠DBE=60°-∠DBA,∠ABC=60°-∠DBA,
∴∠DBE=∠CBA.
易证△DBE≌△CBA,∴DE=AC.
又∵△ACF是等边三角形,
∴AC=AF,∴DE=AF.
同理可得△CBA≌△CDF,∴DF=AB=AE.
∵DE=AF,AE=DF,
∴四边形DEAF是平行四边形.
18.如图,分别以Rt△ABC的直角边AC及斜边AB为边向外作等边△ACD及等边△ABE.已知∠BAC=30°,EF⊥AB于点F,连接DF.求证:
(1)AC=EF;
(2)四边形ADFE是平行四边形.
证明:(1)∵△ABE是等边三角形,EF⊥AB,
∴∠AEF=∠AEB=30°,AE=AB,∠EFA=90°.
易证△AEF≌△BAC,∴AC=EF.
(2)∵△ACD是等边三角形,
∴AC=AD,∠DAC=60°.
由(1)知AC=EF,∴AD=EF.
∵∠BAC=30°,∴∠FAD=∠BAC+∠DAC=90°.
∵∠EFA=90°,∴AD∥EF,
∴四边形ADFE是平行四边形.
19.如图,平行四边形ABCD的对角线AC与BD相交于点O,点E,F分别在OB和OD上,且BE=DF.
(1)求证:四边形AECF是平行四边形;
(2)若∠AEB=90°,OE=3,且∠EAF=45°,求线段AC的长.
解:(1)∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD.
∵BE=DF,∴OB-BE=OD-DF,即OE=OF.
又∵OA=OC,
∴四边形AECF是平行四边形.
(2)由(1)知OF=OE=3,OA=OC.
∵∠AEB=90°,∠EAF=45°,
∴EA=EF=2OE=6,
∴OA==3,
∴AC=2OA=6.
20.如图,在△ABC中,AE平分∠BAC,BE⊥AE于点E,F是边BC的中点.
(1)如图1,BE的延长线与AC边相交于点D,求证:EF=(AC-AB);
(2)如图2,试猜想线段AB,AC,EF的数量关系,并证明.
图1 图2
解:(1)∵AE⊥BD,∴∠AED=∠AEB=90°.
∵AE平分∠BAC,∴∠BAE=∠DAE,
∴∠ABE=∠ADE,∴AB=AD.
∵AE⊥BD,∴BE=DE.
∵BF=FC,
∴EF=(AC-AD)=(AC-AB).
(2)EF=(AB-AC). 证明:延长AC,BE交于点D(过程略).
21.选做题:请在A,B两题中任选一题作答.
A:如图,在△ABC中,AB=AC=20 cm,BD⊥AC于点D,且BD=16 cm.点M从点A出发,沿AC方向匀速运动,速度为4 cm/s;同时点P由点B出发,沿BA方向匀速运动,速度为1 cm/s,过点P的直线PQ∥AC,交BC于点Q,连接PM,设运动时间为t s(0<t<5).当t为何值时,以P,Q,D,M为顶点的四边形是平行四边形?
B:如图,在四边形ABCD中,AB∥CD,AB=24 cm,DC=10 cm,点P自点D向点C以1 cm/s的速度运动,到点C停止.点Q自点B向点A以3 cm/s的速度运动,到点A停止,点P,Q同时出发.试求经过多长时间后,P,Q两点和四边形ABCD的两个顶点所形成的四边形是平行四边形.我选做 题(填A或B),并写出完整的答题过程.
A:解:当t=或t=4时,以P,Q,D,M为顶点的四边形是平行四边形.
B:解:①设经过x s后,四边形PQAD是平行四边形.
根据题意,得x=24-3x,解得x=6,
∴经过6 s后,四边形PQAD是平行四边形.
②设经过y s后,四边形PQBC是平行四边形.
根据题意,得10-y=3y,解得y=2.5,
∴经过2.5 s后,四边形PQBC是平行四边形.
③设经过z s后,四边形PAQC是平行四边形.
根据题意,得10-z=24-3z,解得z=7,
∴经过7 s后,四边形PAQC是平行四边形.
综上所述,经过2.5 s或6 s或7 s后,P,Q两点和梯形ABCD的两个顶点所形成的四边形是平行四边形.
