人教版八年级下册18.2.1.1 矩形的性质 同步练习(含答案)
文档属性
| 名称 | 人教版八年级下册18.2.1.1 矩形的性质 同步练习(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 192.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-31 00:00:00 | ||
图片预览

文档简介
第十八章 平行四边形
18.2.1 矩形
第1课时 矩形的性质
一、选择题
1.若矩形的一边长为6,一条对角线的长为10,则该矩形的另一边长为( )
A.6 B.8 C.10 D.16
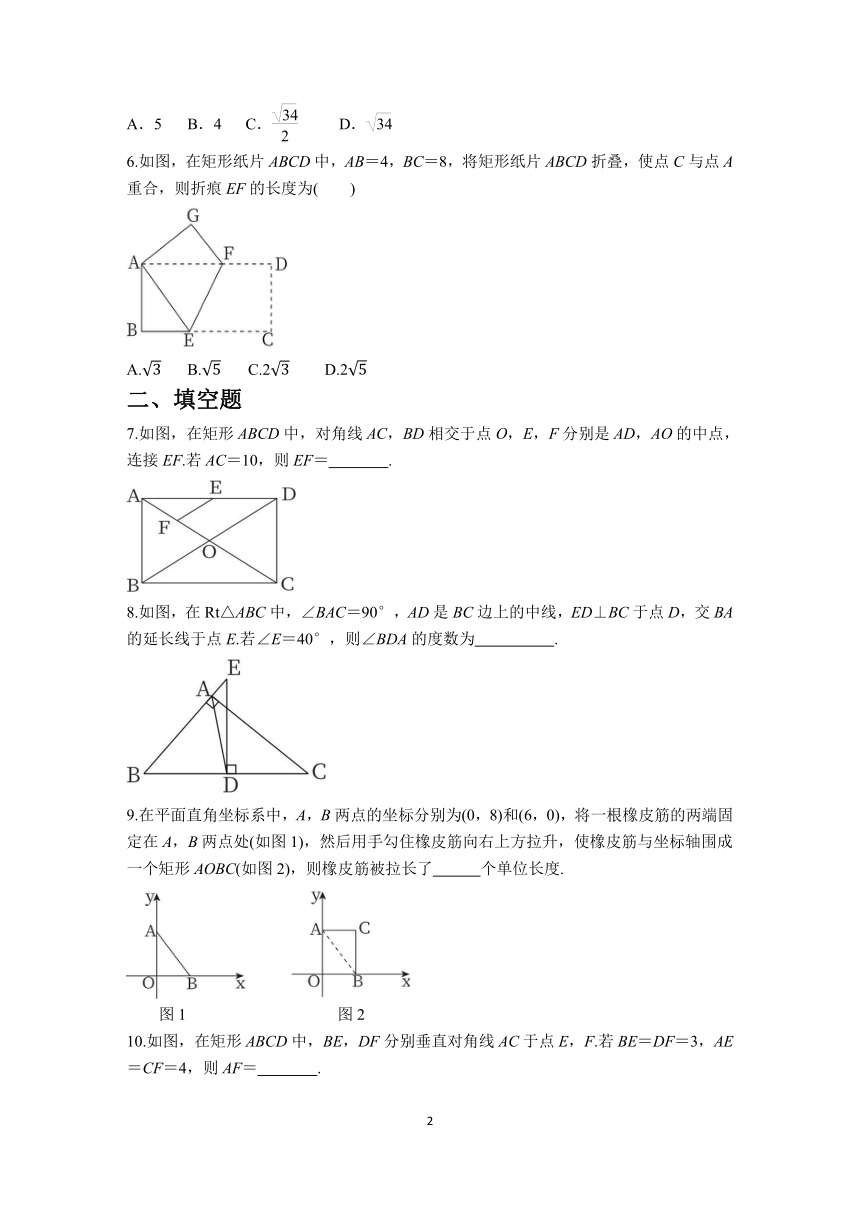
2.如图,在矩形ABCD中,对角线AC,BD相交于点O.若∠AOB=60°,AB=2,则BD的长是( )
A. B.2 C.2 D.4
3.如图,公路AC,BC互相垂直,M为公路AB的中点.若测得AB的长为5 km,则C,M两点间的距离为( )
A.2.5 km B.3 km C.4.5 km D.5 km
4.如图,延长矩形ABCD的边BC至点E,使CE=BD,连接AE.若∠ADB=40°,则∠E的度数是( )
A.20° B.25° C.30° D.35°
5.如图,点O是矩形ABCD的对角线AC的中点,OM∥AB交AD于点M,若OM=3,BC=10,则OB的长为( )
A.5 B.4 C. D.
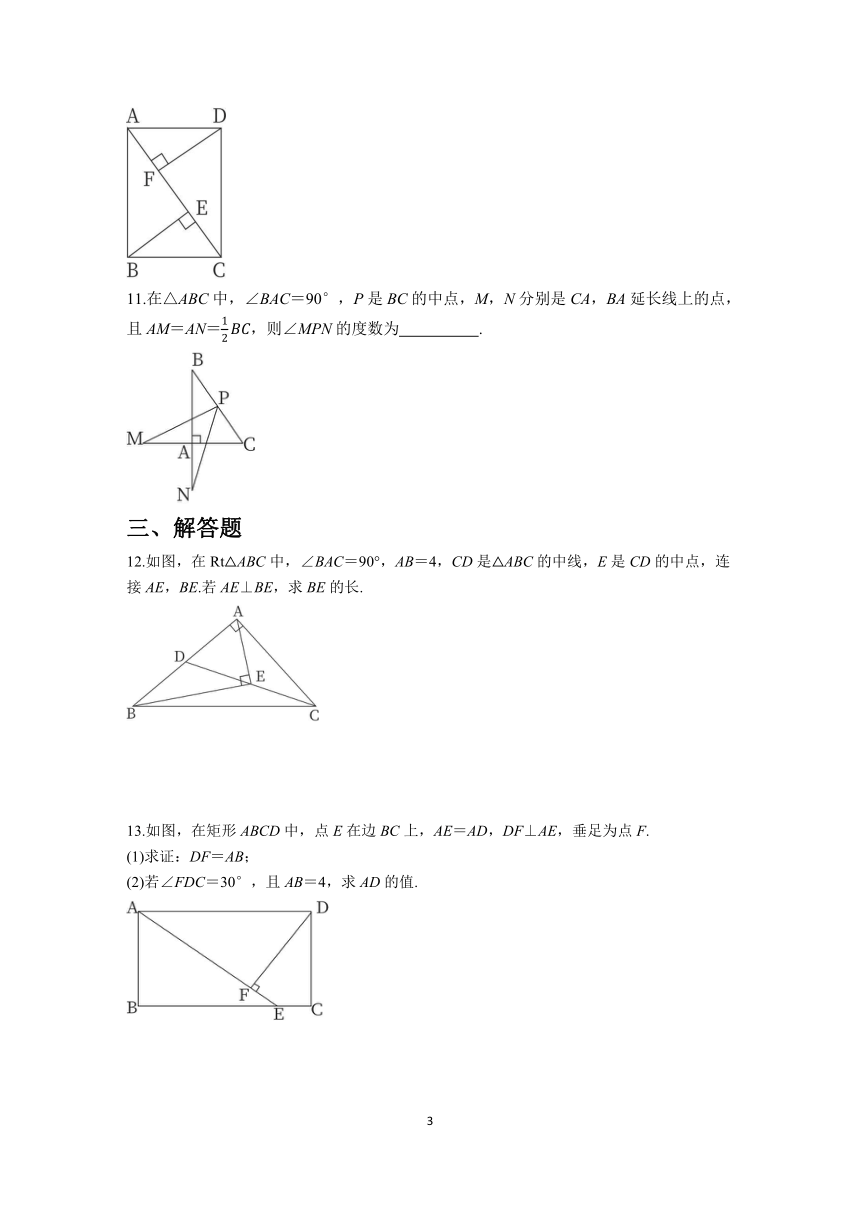
6.如图,在矩形纸片ABCD中,AB=4,BC=8,将矩形纸片ABCD折叠,使点C与点A重合,则折痕EF的长度为( )
A. B. C.2 D.2
二、填空题
7.如图,在矩形ABCD中,对角线AC,BD相交于点O,E,F分别是AD,AO的中点,连接EF.若AC=10,则EF= .
8.如图,在Rt△ABC中,∠BAC=90°,AD是BC边上的中线,ED⊥BC于点D,交BA的延长线于点E.若∠E=40°,则∠BDA的度数为 .
9.在平面直角坐标系中,A,B两点的坐标分别为(0,8)和(6,0),将一根橡皮筋的两端固定在A,B两点处(如图1),然后用手勾住橡皮筋向右上方拉升,使橡皮筋与坐标轴围成一个矩形AOBC(如图2),则橡皮筋被拉长了 个单位长度.
图1 图2
10.如图,在矩形ABCD中,BE,DF分别垂直对角线AC于点E,F.若BE=DF=3,AE=CF=4,则AF= .
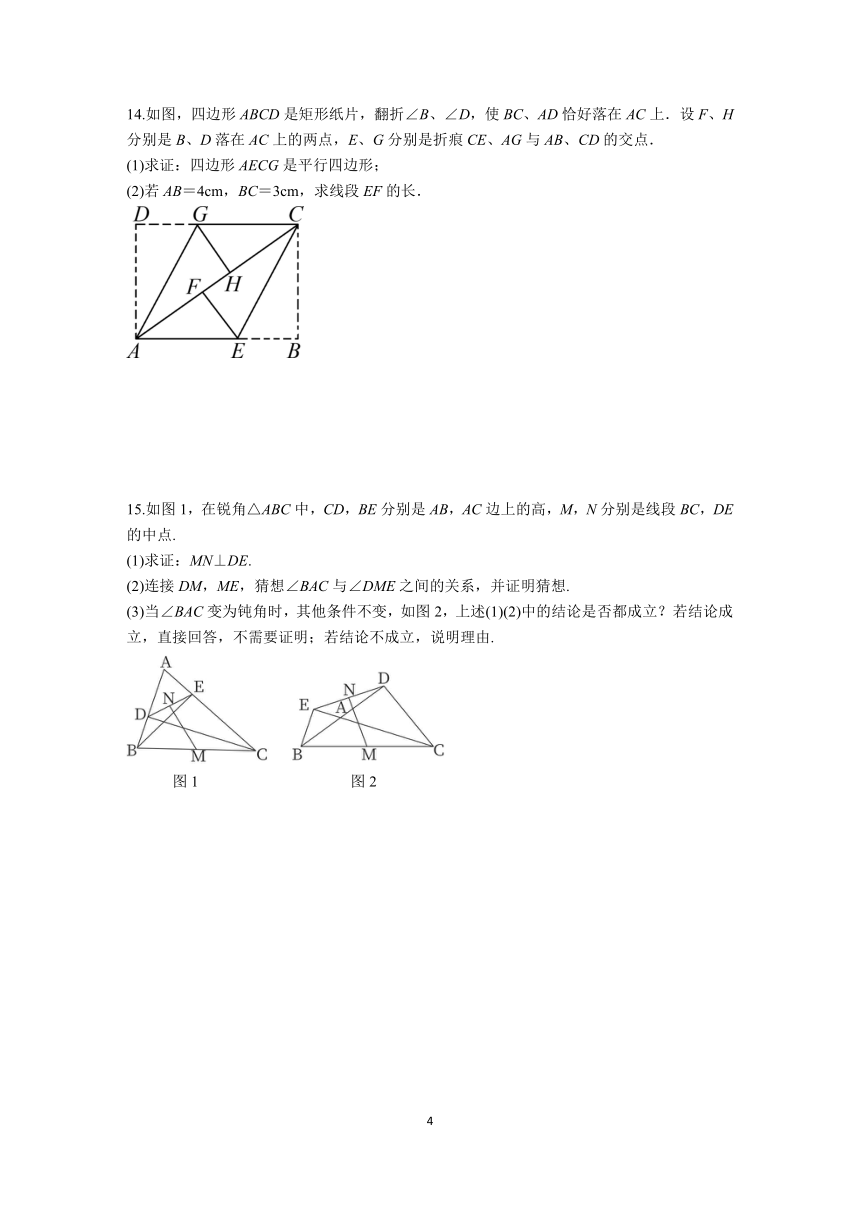
11.在△ABC中,∠BAC=90°,P是BC的中点,M,N分别是CA,BA延长线上的点,且AM=AN=,则∠MPN的度数为 .
三、解答题
12.如图,在Rt△ABC中,∠BAC=90°,AB=4,CD是△ABC的中线,E是CD的中点,连接AE,BE.若AE⊥BE,求BE的长.
13.如图,在矩形ABCD中,点E在边BC上,AE=AD,DF⊥AE,垂足为点F.
(1)求证:DF=AB;
(2)若∠FDC=30°,且AB=4,求AD的值.
14.如图,四边形ABCD是矩形纸片,翻折∠B、∠D,使BC、AD恰好落在AC上.设F、H分别是B、D落在AC上的两点,E、G分别是折痕CE、AG与AB、CD的交点.
(1)求证:四边形AECG是平行四边形;
(2)若AB=4cm,BC=3cm,求线段EF的长.
15.如图1,在锐角△ABC中,CD,BE分别是AB,AC边上的高,M,N分别是线段BC,DE的中点.
(1)求证:MN⊥DE.
(2)连接DM,ME,猜想∠BAC与∠DME之间的关系,并证明猜想.
(3)当∠BAC变为钝角时,其他条件不变,如图2,上述(1)(2)中的结论是否都成立?若结论成立,直接回答,不需要证明;若结论不成立,说明理由.
图1 图2
1
参考答案
一、选择题
1.若矩形的一边长为6,一条对角线的长为10,则该矩形的另一边长为( B )
A.6 B.8 C.10 D.16
2.如图,在矩形ABCD中,对角线AC,BD相交于点O.若∠AOB=60°,AB=2,则BD的长是( D )
A. B.2 C.2 D.4
3.如图,公路AC,BC互相垂直,M为公路AB的中点.若测得AB的长为5 km,则C,M两点间的距离为( A )
A.2.5 km B.3 km C.4.5 km D.5 km
4.如图,延长矩形ABCD的边BC至点E,使CE=BD,连接AE.若∠ADB=40°,则∠E的度数是( A )
A.20° B.25° C.30° D.35°
5.如图,点O是矩形ABCD的对角线AC的中点,OM∥AB交AD于点M,若OM=3,BC=10,则OB的长为( D )
A.5 B.4 C. D.
6.如图,在矩形纸片ABCD中,AB=4,BC=8,将矩形纸片ABCD折叠,使点C与点A重合,则折痕EF的长度为( D )
A. B. C.2 D.2
二、填空题
7.如图,在矩形ABCD中,对角线AC,BD相交于点O,E,F分别是AD,AO的中点,连接EF.若AC=10,则EF= .
【答案】
8.如图,在Rt△ABC中,∠BAC=90°,AD是BC边上的中线,ED⊥BC于点D,交BA的延长线于点E.若∠E=40°,则∠BDA的度数为 .
【答案】80°
9.在平面直角坐标系中,A,B两点的坐标分别为(0,8)和(6,0),将一根橡皮筋的两端固定在A,B两点处(如图1),然后用手勾住橡皮筋向右上方拉升,使橡皮筋与坐标轴围成一个矩形AOBC(如图2),则橡皮筋被拉长了 个单位长度.
图1 图2
【答案】4
10.如图,在矩形ABCD中,BE,DF分别垂直对角线AC于点E,F.若BE=DF=3,AE=CF=4,则AF= .
【答案】
11.在△ABC中,∠BAC=90°,P是BC的中点,M,N分别是CA,BA延长线上的点,且AM=AN=,则∠MPN的度数为 .
【答案】45°
三、解答题
12.如图,在Rt△ABC中,∠BAC=90°,AB=4,CD是△ABC的中线,E是CD的中点,连接AE,BE.若AE⊥BE,求BE的长.
解:∵AE⊥BE,∴∠AEB=90°.
∵D是AB的中点,AB=4,
∴DE==2.
∵∠DAC=90°,E是CD的中点,
∴AE=DE=2,
∴BE==2.
13.如图,在矩形ABCD中,点E在边BC上,AE=AD,DF⊥AE,垂足为点F.
(1)求证:DF=AB;
(2)若∠FDC=30°,且AB=4,求AD的值.
解:(1)在矩形ABCD中,∵AD∥BC,
∴∠AEB=∠DAF.
又∵DF⊥AE,∴∠DFA=90°=∠B.
又∵AD=EA,∴△ADF≌△EAB(AAS),
∴DF=AB.
(2)∵∠ADF+∠FDC=90°,∠DAF+∠ADF=90°,
∴∠DAF=∠FDC=30°,∴AD=2DF.
∵DF=AB=4,∴AD=8.
14.如图,四边形ABCD是矩形纸片,翻折∠B、∠D,使BC、AD恰好落在AC上.设F、H分别是B、D落在AC上的两点,E、G分别是折痕CE、AG与AB、CD的交点.
(1)求证:四边形AECG是平行四边形;
(2)若AB=4cm,BC=3cm,求线段EF的长.
(1)证明:在矩形ABCD中,∵AD∥BC,∴∠DAC=∠BCA.由题意,得∠GAH=∠DAC,∠ECF=∠BCA,∴∠GAH=∠ECF,∴AG∥CE.又∵AE∥CG,∴四边形AECG是平行四边形;
(2)解:在Rt△ABC中,∵AB=4,BC=3,∴AC=5.∵CF=CB=3,∴AF=2.在Rt△AEF中,设EF=x,则AE=(4-x).根据勾股定理,得AE2=AF2+EF2,即(4-x)2=22+x2,解得x=,即线段EF的长为cm.
15.如图1,在锐角△ABC中,CD,BE分别是AB,AC边上的高,M,N分别是线段BC,DE的中点.
(1)求证:MN⊥DE.
(2)连接DM,ME,猜想∠BAC与∠DME之间的关系,并证明猜想.
(3)当∠BAC变为钝角时,其他条件不变,如图2,上述(1)(2)中的结论是否都成立?若结论成立,直接回答,不需要证明;若结论不成立,说明理由.
图1 图2
解:(1)证明略.
(2)∠DME=180°-2∠BAC.
证明:∵DM=ME=BM=MC,
∴∠BMD+∠CME=(180°-2∠ABC)+(180°-2∠ACB)=360°-2(∠ABC+∠ACB)=360°-2(180°-∠BAC)=2∠BAC,
∴∠DME=180°-2∠BAC.
(3)结论(1)成立,结论(2)不成立.
理由:∵DM=ME=BM=MC,
∴∠BME+∠CMD=2∠ACB+2∠ABC=2(180°-∠BAC)=360°-2∠BAC,
∴∠DME=180°-(360°-2∠BAC)=2∠BAC-180°.
18.2.1 矩形
第1课时 矩形的性质
一、选择题
1.若矩形的一边长为6,一条对角线的长为10,则该矩形的另一边长为( )
A.6 B.8 C.10 D.16
2.如图,在矩形ABCD中,对角线AC,BD相交于点O.若∠AOB=60°,AB=2,则BD的长是( )
A. B.2 C.2 D.4
3.如图,公路AC,BC互相垂直,M为公路AB的中点.若测得AB的长为5 km,则C,M两点间的距离为( )
A.2.5 km B.3 km C.4.5 km D.5 km
4.如图,延长矩形ABCD的边BC至点E,使CE=BD,连接AE.若∠ADB=40°,则∠E的度数是( )
A.20° B.25° C.30° D.35°
5.如图,点O是矩形ABCD的对角线AC的中点,OM∥AB交AD于点M,若OM=3,BC=10,则OB的长为( )
A.5 B.4 C. D.
6.如图,在矩形纸片ABCD中,AB=4,BC=8,将矩形纸片ABCD折叠,使点C与点A重合,则折痕EF的长度为( )
A. B. C.2 D.2
二、填空题
7.如图,在矩形ABCD中,对角线AC,BD相交于点O,E,F分别是AD,AO的中点,连接EF.若AC=10,则EF= .
8.如图,在Rt△ABC中,∠BAC=90°,AD是BC边上的中线,ED⊥BC于点D,交BA的延长线于点E.若∠E=40°,则∠BDA的度数为 .
9.在平面直角坐标系中,A,B两点的坐标分别为(0,8)和(6,0),将一根橡皮筋的两端固定在A,B两点处(如图1),然后用手勾住橡皮筋向右上方拉升,使橡皮筋与坐标轴围成一个矩形AOBC(如图2),则橡皮筋被拉长了 个单位长度.
图1 图2
10.如图,在矩形ABCD中,BE,DF分别垂直对角线AC于点E,F.若BE=DF=3,AE=CF=4,则AF= .
11.在△ABC中,∠BAC=90°,P是BC的中点,M,N分别是CA,BA延长线上的点,且AM=AN=,则∠MPN的度数为 .
三、解答题
12.如图,在Rt△ABC中,∠BAC=90°,AB=4,CD是△ABC的中线,E是CD的中点,连接AE,BE.若AE⊥BE,求BE的长.
13.如图,在矩形ABCD中,点E在边BC上,AE=AD,DF⊥AE,垂足为点F.
(1)求证:DF=AB;
(2)若∠FDC=30°,且AB=4,求AD的值.
14.如图,四边形ABCD是矩形纸片,翻折∠B、∠D,使BC、AD恰好落在AC上.设F、H分别是B、D落在AC上的两点,E、G分别是折痕CE、AG与AB、CD的交点.
(1)求证:四边形AECG是平行四边形;
(2)若AB=4cm,BC=3cm,求线段EF的长.
15.如图1,在锐角△ABC中,CD,BE分别是AB,AC边上的高,M,N分别是线段BC,DE的中点.
(1)求证:MN⊥DE.
(2)连接DM,ME,猜想∠BAC与∠DME之间的关系,并证明猜想.
(3)当∠BAC变为钝角时,其他条件不变,如图2,上述(1)(2)中的结论是否都成立?若结论成立,直接回答,不需要证明;若结论不成立,说明理由.
图1 图2
1
参考答案
一、选择题
1.若矩形的一边长为6,一条对角线的长为10,则该矩形的另一边长为( B )
A.6 B.8 C.10 D.16
2.如图,在矩形ABCD中,对角线AC,BD相交于点O.若∠AOB=60°,AB=2,则BD的长是( D )
A. B.2 C.2 D.4
3.如图,公路AC,BC互相垂直,M为公路AB的中点.若测得AB的长为5 km,则C,M两点间的距离为( A )
A.2.5 km B.3 km C.4.5 km D.5 km
4.如图,延长矩形ABCD的边BC至点E,使CE=BD,连接AE.若∠ADB=40°,则∠E的度数是( A )
A.20° B.25° C.30° D.35°
5.如图,点O是矩形ABCD的对角线AC的中点,OM∥AB交AD于点M,若OM=3,BC=10,则OB的长为( D )
A.5 B.4 C. D.
6.如图,在矩形纸片ABCD中,AB=4,BC=8,将矩形纸片ABCD折叠,使点C与点A重合,则折痕EF的长度为( D )
A. B. C.2 D.2
二、填空题
7.如图,在矩形ABCD中,对角线AC,BD相交于点O,E,F分别是AD,AO的中点,连接EF.若AC=10,则EF= .
【答案】
8.如图,在Rt△ABC中,∠BAC=90°,AD是BC边上的中线,ED⊥BC于点D,交BA的延长线于点E.若∠E=40°,则∠BDA的度数为 .
【答案】80°
9.在平面直角坐标系中,A,B两点的坐标分别为(0,8)和(6,0),将一根橡皮筋的两端固定在A,B两点处(如图1),然后用手勾住橡皮筋向右上方拉升,使橡皮筋与坐标轴围成一个矩形AOBC(如图2),则橡皮筋被拉长了 个单位长度.
图1 图2
【答案】4
10.如图,在矩形ABCD中,BE,DF分别垂直对角线AC于点E,F.若BE=DF=3,AE=CF=4,则AF= .
【答案】
11.在△ABC中,∠BAC=90°,P是BC的中点,M,N分别是CA,BA延长线上的点,且AM=AN=,则∠MPN的度数为 .
【答案】45°
三、解答题
12.如图,在Rt△ABC中,∠BAC=90°,AB=4,CD是△ABC的中线,E是CD的中点,连接AE,BE.若AE⊥BE,求BE的长.
解:∵AE⊥BE,∴∠AEB=90°.
∵D是AB的中点,AB=4,
∴DE==2.
∵∠DAC=90°,E是CD的中点,
∴AE=DE=2,
∴BE==2.
13.如图,在矩形ABCD中,点E在边BC上,AE=AD,DF⊥AE,垂足为点F.
(1)求证:DF=AB;
(2)若∠FDC=30°,且AB=4,求AD的值.
解:(1)在矩形ABCD中,∵AD∥BC,
∴∠AEB=∠DAF.
又∵DF⊥AE,∴∠DFA=90°=∠B.
又∵AD=EA,∴△ADF≌△EAB(AAS),
∴DF=AB.
(2)∵∠ADF+∠FDC=90°,∠DAF+∠ADF=90°,
∴∠DAF=∠FDC=30°,∴AD=2DF.
∵DF=AB=4,∴AD=8.
14.如图,四边形ABCD是矩形纸片,翻折∠B、∠D,使BC、AD恰好落在AC上.设F、H分别是B、D落在AC上的两点,E、G分别是折痕CE、AG与AB、CD的交点.
(1)求证:四边形AECG是平行四边形;
(2)若AB=4cm,BC=3cm,求线段EF的长.
(1)证明:在矩形ABCD中,∵AD∥BC,∴∠DAC=∠BCA.由题意,得∠GAH=∠DAC,∠ECF=∠BCA,∴∠GAH=∠ECF,∴AG∥CE.又∵AE∥CG,∴四边形AECG是平行四边形;
(2)解:在Rt△ABC中,∵AB=4,BC=3,∴AC=5.∵CF=CB=3,∴AF=2.在Rt△AEF中,设EF=x,则AE=(4-x).根据勾股定理,得AE2=AF2+EF2,即(4-x)2=22+x2,解得x=,即线段EF的长为cm.
15.如图1,在锐角△ABC中,CD,BE分别是AB,AC边上的高,M,N分别是线段BC,DE的中点.
(1)求证:MN⊥DE.
(2)连接DM,ME,猜想∠BAC与∠DME之间的关系,并证明猜想.
(3)当∠BAC变为钝角时,其他条件不变,如图2,上述(1)(2)中的结论是否都成立?若结论成立,直接回答,不需要证明;若结论不成立,说明理由.
图1 图2
解:(1)证明略.
(2)∠DME=180°-2∠BAC.
证明:∵DM=ME=BM=MC,
∴∠BMD+∠CME=(180°-2∠ABC)+(180°-2∠ACB)=360°-2(∠ABC+∠ACB)=360°-2(180°-∠BAC)=2∠BAC,
∴∠DME=180°-2∠BAC.
(3)结论(1)成立,结论(2)不成立.
理由:∵DM=ME=BM=MC,
∴∠BME+∠CMD=2∠ACB+2∠ABC=2(180°-∠BAC)=360°-2∠BAC,
∴∠DME=180°-(360°-2∠BAC)=2∠BAC-180°.
