人教版七年级下册 第8章 二元一次方程组 单元测试卷(能力提升) 含详解
文档属性
| 名称 | 人教版七年级下册 第8章 二元一次方程组 单元测试卷(能力提升) 含详解 |

|
|
| 格式 | doc | ||
| 文件大小 | 386.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-30 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
人教版七年级下册 第8章 二元一次方程组 单元测试卷(能力提升)
满分120分
一.选择题(共10小题,满分30分,每小题3分)
1.|m﹣2|x+3y|m﹣1|=23是关于x,y的二元一次方程,则m=( )
A.2 B.0 C.1 D.—1
2.下列哪对x,y的值是二元一次方程x+2y=6的解( )
A. B. C. D.
3.用加减消元法解方程组,下列做法正确的是( )
A.①+② B.①﹣② C.①+②×5 D.①×5﹣②
4.在等式y=kx+b中,当x=1时,y=﹣2;当x=﹣1时,y=﹣4.则2k+b的值为( )
A.1 B.﹣1 C.﹣2 D.﹣3
5.已知方程组的解满足x﹣y=3,则k的值为( )
A.﹣2 B.2 C.﹣1 D.1
6.已知是二元一次方程组的解,则4a﹣5b的平方根为( )
A. B.2 C.± D.±2
7.方程组的解为,则被△和▽遮盖的两个数分别为( )
A.﹣10,6 B.2,﹣6 C.2,6 D.10,﹣6
8.在解关于x、y的方程组时甲看错①中的a,解得x=4,y=2,乙看错②中的b,解得x=﹣3,y=﹣1,则a和b的正确值应是( )
A.a=﹣4.25,b=3 B.a=4,b=13
C.a=4,b=4 D.a=﹣5,b=4
9.成都大熊猫繁育研究基地是全国热门景点,某店家推出了纪念品礼盒深受国内外游客喜爱,一个礼盒里包含1个花花玩偶和3个花花钥匙扣.已知一个玩偶的进价为50元,一个钥匙扣的进价为10元,该店家计划用8000元购进一批玩偶和钥匙扣,使得刚好配套,设购进x个玩偶,y个钥匙扣,则下列方程组正确的是( )
A. B.
C. D.
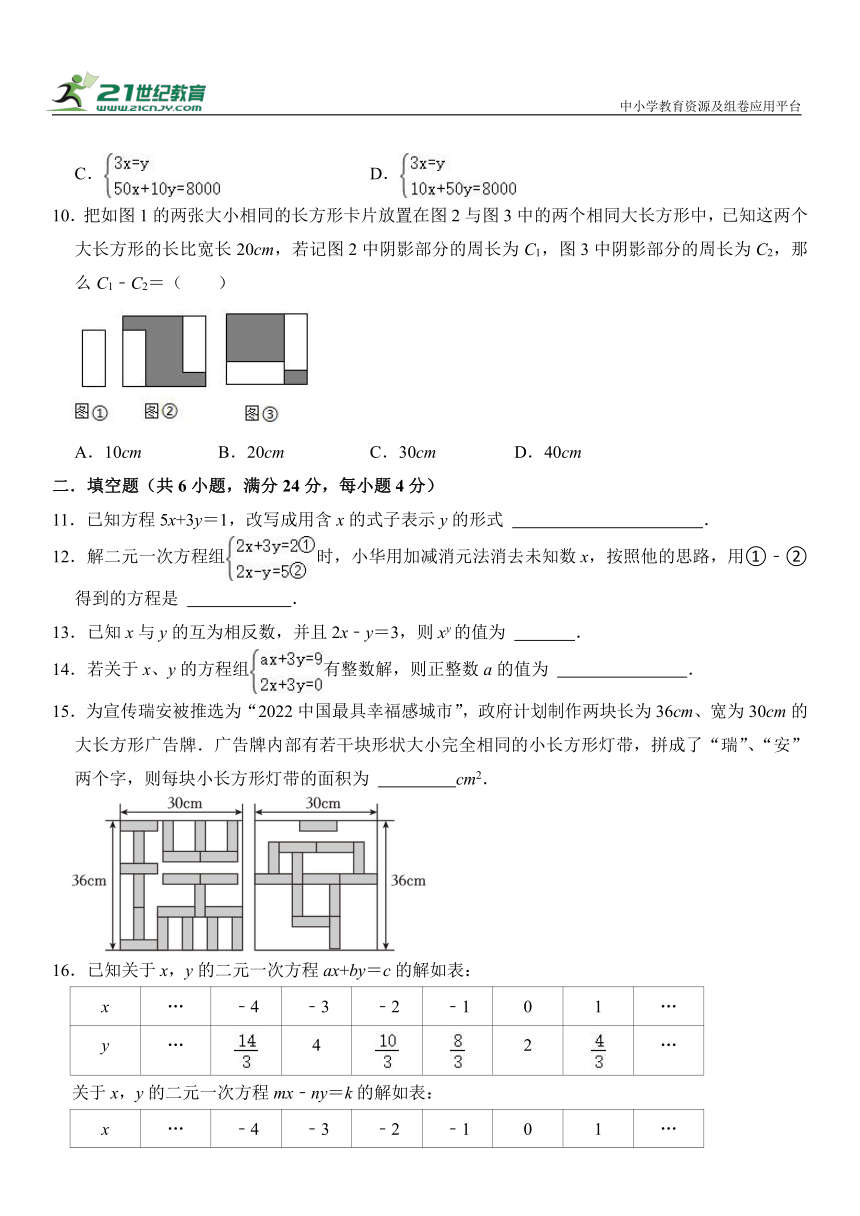
10.把如图1的两张大小相同的长方形卡片放置在图2与图3中的两个相同大长方形中,已知这两个大长方形的长比宽长20cm,若记图2中阴影部分的周长为C1,图3中阴影部分的周长为C2,那么C1﹣C2=( )
A.10cm B.20cm C.30cm D.40cm
二.填空题(共6小题,满分24分,每小题4分)
11.已知方程5x+3y=1,改写成用含x的式子表示y的形式 .
12.解二元一次方程组时,小华用加减消元法消去未知数x,按照他的思路,用①﹣②得到的方程是 .
13.已知x与y的互为相反数,并且2x﹣y=3,则xy的值为 .
14.若关于x、y的方程组有整数解,则正整数a的值为 .
15.为宣传瑞安被推选为“2022中国最具幸福感城市”,政府计划制作两块长为36cm、宽为30cm的大长方形广告牌.广告牌内部有若干块形状大小完全相同的小长方形灯带,拼成了“瑞”、“安”两个字,则每块小长方形灯带的面积为 cm2.
16.已知关于x,y的二元一次方程ax+by=c的解如表:
x … ﹣4 ﹣3 ﹣2 ﹣1 0 1 …
y … 4 2 …
关于x,y的二元一次方程mx﹣ny=k的解如表:
x … ﹣4 ﹣3 ﹣2 ﹣1 0 1 …
y … 4 1 ﹣2 …
则关于x,y的二元一次方程组的解是 .
三.解答题(共7小题,满分66分)
17.(8分)解方程组:
(1); (2).
18.(6分)解方程组:.
19.(9分)如果某个二元一次方程组的解中两个未知数的值是互为相反数,我们称这个方程组为“关联方程组”.
(1)判断方程组是不是“关联方程组”,并说明理由;
(2)如果关于x,y的方程组是“关联方程组”,求a的值.
20.(9分)已知关于x,y的二元一次方程组与方程组有相同的解.
(1)求这两个方程组的相同解;
(2)求(2a+b)2024的值.
21.(10分)阅读以下材料:
解方程组:,小阳在解决这个问题时,发现了一种新的方法,他把这种方法叫做“整体代入法”,解题过程如下:
解:由①得x+y=1③,将③代入②得:
(1)请你替小阳补全完整的解题过程;
(2)请你用这种方法解方程组:.
22.(12分)某体育用品商场销售A,B两款足球,售价和进价如表:
类型 进价(元/个) 售价(元/个)
A款 m 120
B款 n 90
若该商场购进5个A款足球和12个B款足球需1120元;若该商场购进10个A款足球和15个B款足球需1700元.
(1)求m和n的值;
(2)某校在该商场一次性购买A款足球x个和B款足球y个,共消费3300元,那么该商场可获利多少元?
(3)为了提高销量,商场实施:“买足球送跳绳”的促销活动:“买1个A款足球送1根跳绳,买3个B款足球送2根跳绳”,每根跳绳的成本为10元,某日售卖出两款足球总计盈利600元,那么该日商场销售A、B两款足球各多少个?(每款都有销售)
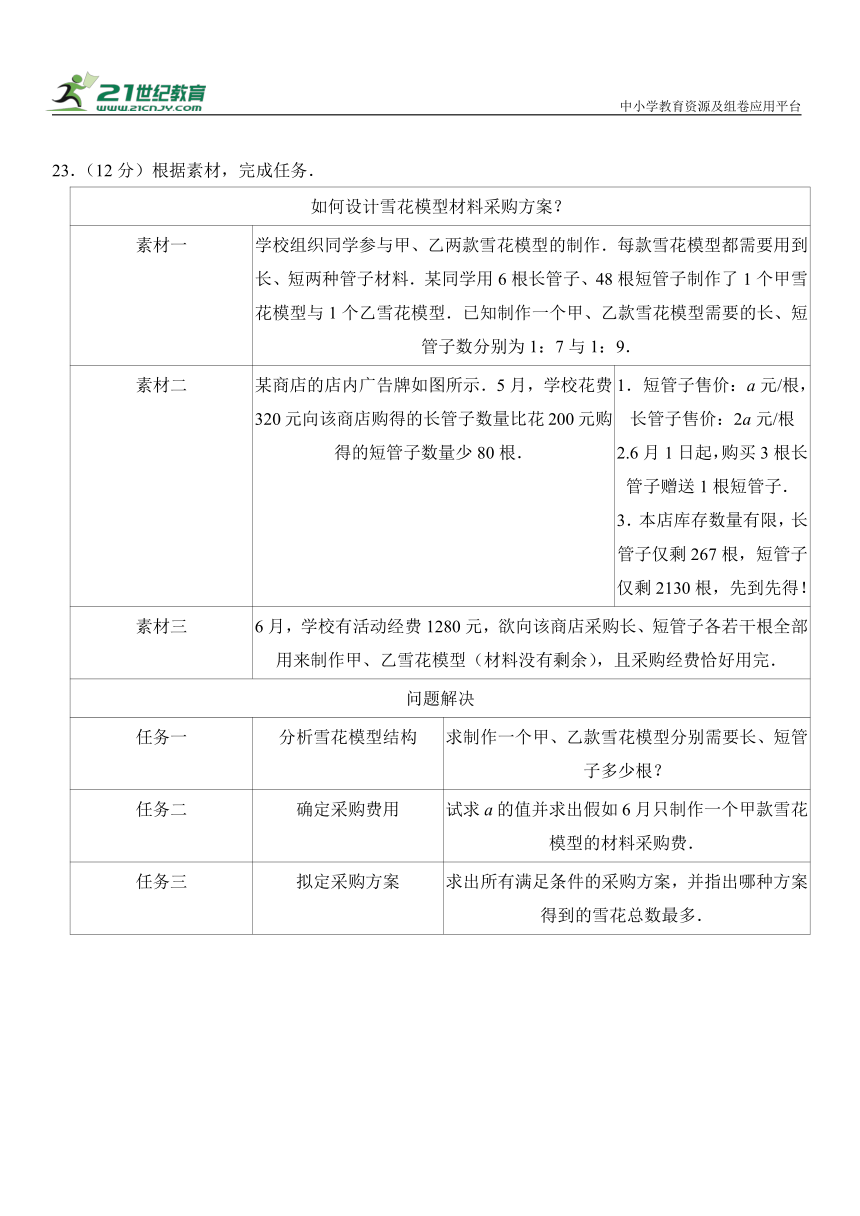
23.(12分)根据素材,完成任务.
如何设计雪花模型材料采购方案?
素材一 学校组织同学参与甲、乙两款雪花模型的制作.每款雪花模型都需要用到长、短两种管子材料.某同学用6根长管子、48根短管子制作了1个甲雪花模型与1个乙雪花模型.已知制作一个甲、乙款雪花模型需要的长、短管子数分别为1:7与1:9.
素材二 某商店的店内广告牌如图所示.5月,学校花费320元向该商店购得的长管子数量比花200元购得的短管子数量少80根. 1.短管子售价:a元/根,长管子售价:2a元/根2.6月1日起,购买3根长管子赠送1根短管子.3.本店库存数量有限,长管子仅剩267根,短管子仅剩2130根,先到先得!
素材三 6月,学校有活动经费1280元,欲向该商店采购长、短管子各若干根全部用来制作甲、乙雪花模型(材料没有剩余),且采购经费恰好用完.
问题解决
任务一 分析雪花模型结构 求制作一个甲、乙款雪花模型分别需要长、短管子多少根?
任务二 确定采购费用 试求a的值并求出假如6月只制作一个甲款雪花模型的材料采购费.
任务三 拟定采购方案 求出所有满足条件的采购方案,并指出哪种方案得到的雪花总数最多.
参考答案
一.选择题
1.解:∵|m﹣2|x+3y|m﹣1|=23是关于x,y的二元一次方程,
∴,
解得m=0.
故选:B.
2.解:A.当x=﹣2,y=﹣2,得x+2y=﹣6,那么x=﹣2,y=﹣2不是x+2y=6的解,故A不符合题意.
B.当x=0,y=2,得x+2y=4,那么x=0,y=2不是x+2y=6的解,故B不符合题意.
C.当x=2,y=2,得x+2y=2+4=6,那么x=2,y=2是x+2y=6的解,故C符合题意.
D.当x=3,y=1,得x+2y=3+2=5,那么x=3,y=1不是x+2y=6的解,故D不符合题意.
故选:C.
3.解:若消去y,
则①+②得:6x=﹣16;
若消去x,
则①﹣②×5得:﹣12y=98;
故选:A.
4.解:由题意可得,
①+②,得b=﹣3,
将b=﹣3代入①得,k=1,
∴2k+b=2﹣3=﹣1,
故选:B.
5.解:,
②﹣①,得:x﹣y=1﹣k,
∵x﹣y=3,
∴1﹣k=3,
解得:k=﹣2,
故选:A.
6.解:把代入二元一次方程组得:,
解得:,
4a﹣5b=12﹣10=2,
2的平方根为:.
故选:C.
7.解:∵方程组的解为,
∴﹣2﹣y=4,
解得:y=﹣6,
∴▽=﹣6,
∴Δ=2×(﹣2)﹣(﹣6)=2,
∴被△和▽遮盖的两个数分别为2,﹣6.
故选:B.
8.解:将x=4,y=2代入3x﹣by=4得12﹣2b=4,
解得:b=4,
将x=﹣3,y=﹣1代入ax+8y=7得﹣3a﹣8=7,
解得:a=﹣5,
故选:D.
9.解:∵一个礼盒里包含1个花花玩偶和3个花花钥匙扣,且购进的偶和钥匙扣刚好配套,
∴3x=y;
∵该店家计划用8000元购进一批玩偶和钥匙扣,且一个玩偶的进价为50元,一个钥匙扣的进价为10元,
∴50x+10y=8000.
∴根据题意可列方程组.
故选:C.
10.解:设大长方形的宽为a cm,则长为(a+20)cm,图①中的长方形长为x cm,宽为y cm,
图②中阴影部分的周长C1为:2[(a+20)+a]=(4a+40)cm,
由图③可得,x+y=a+20,
图③中阴影部分的周长C2为:2(a+20)+2(a﹣y)+2(a﹣x)=2(3a+20﹣x﹣y)=2(3a+20﹣a﹣20)=4a(cm),
C1﹣C2=(4a+40)﹣4a
=4a+40﹣4a
=40(cm).
故选:D.
二.填空题
11.解:5x+3y=1,
3y=1﹣5x,
y=.
故答案为:y=.
12.解:解二元一次方程组时,小华用加减消元法消去未知数x,按照他的思路,用①﹣②得到的方程是:4y=﹣3,
故答案为:4y=﹣3.
13.解:∵x与y互为相反数,
∴x+y=0,
∴,
①+②,得3x=3,
解得x=1,
∴y=﹣1,
∴xy=1﹣1=1.
故答案为:1.
14.解:,
由②得:③,
把③代入①得:,
把代入③得:,
∵关于x、y的方程组有整数解,
∴a﹣2=±1或±3或±9,2﹣a=±1或±2或±3或±6,
解得:a=±1或3或5,
∴正整数a的值为:1或3或5.
故答案为:1或3或5.
15.解:设每块小长方形灯带的长为x cm,宽为y cm,
由题意得:,
解得:,
∴xy=9×3=27,
即每块小长方形灯带的面积为27cm2,
故答案为:27.
16.解:由表可得:的解为:,
∴二元一次方程组的解为:,
解得:,
故答案为:.
三.解答题
17.解:(1),
将②代入①得:2(y+1)+3y=22,
整理得:5y+2=22,
解得:y=4,
将y=4代入②得:x=4+1=5,
故原方程组的解为;
(2),
①×2+②得:8x=18,
解得:x=,
将x=代入②得:﹣4y=4,
解得:y=,
故原方程组的解为.
18.解:,
②+③得:
3x+y=﹣1④,
④×3得:
9x+3y=﹣3⑤,
⑤﹣①得:
7x=﹣7,
解得:x=﹣1,
把x=﹣1代入①得:
﹣2+3y=4,
解得:y=2,
把x=﹣1,y=2代入②得:
﹣2﹣2+2z=﹣4,
解得:z=0,
∴原方程组的解为:.
19.解:(1)方程组是“关联方程组”,理由如下:
,
(①﹣②)÷2得:x+y=0,
∴方程组是“关联方程组”;
(2),
(①+②)÷2得:x+y=2+a.
又∵关于x,y的方程组是“关联方程组”,
∴x+y=2+a=0,
解得:a=﹣2,
∴a的值为﹣2.
20.解:(1)由题意,得,
①+②,得5x=10,解得x=2.
把x=2代入①,得4+5y=﹣26,解得y=﹣6.
∴这两个方程组的相同解为
(2)把代入得:
解此方程组,
得a=1,b=﹣1,
∴(2a+b)2024=(2﹣1)2024=1.
21.解:(1)由①得x+y=1③,
将③代入②得3×1+y=2,
解得y=﹣1,
把y=﹣1代入①得,
x﹣1﹣1=0,
解得x=2,
故原方程组的解是;
(2)整理得,
,
把①代入②得,
2×(﹣1)+2+6y=12,
解得y=2,
把y=2代入①得,
3x﹣2=﹣1,
解得x=,
故原方程组的解是.
22.解:(1)根据题意得:,
解得:,
∴m的值为80,n的值为60;
(2)根据题意得:120x+90y=3300,
∴40x+30y=1100,
∴(120﹣80)x+(90﹣60)y=40x+30y=1100.
答:该商场可获利1100元;
(3)设该日商场销售a个A款足球,3b个B款足球,
根据题意得:(120﹣80﹣10)a+(90×3﹣60×3﹣10×2)b=600,
∴a=20﹣b,
又∵a,b均为正整数,
∴或,
∴或.
答:该日商场销售13个A款足球、9个B款足球或6个A款足球、18个B款足球.
23.任务一:假设制作一个甲乙款雪花模型分别需要长管子的个数为x,y,则需要短管为7x,9y,
则,
解得,
所以制作甲乙款雪花模型分别需要长管子的个数分别为3,3,短管子的个数为21,27.
任务二:由题意得,
解得:a=,
3×l+(21﹣1)×=13(元);
任务三:假设制作甲款雪花模型m个,乙款n个则需要长管子(3m+3n)个,短管子(21m+2m)个,
由题意可得:(3m+3n)(21m+27n﹣)=1280,
化简得到13m+16n=1280,
解得:,,,,
显然 0+40<16+27<32+14<48+1,
对应的采购方案为:
(1)长管购买1201,赠40短管,购买短管1080个,
(2)长管购买1299,赠43管,购买短管1065个,
(3)长管购买138个,赠46管购买短管1050个,
(4)长管购买147T赠49管购买短管1035个,
其中方案(4)雪花总数最多,为49个.
人教版七年级下册 第8章 二元一次方程组 单元测试卷(能力提升)
满分120分
一.选择题(共10小题,满分30分,每小题3分)
1.|m﹣2|x+3y|m﹣1|=23是关于x,y的二元一次方程,则m=( )
A.2 B.0 C.1 D.—1
2.下列哪对x,y的值是二元一次方程x+2y=6的解( )
A. B. C. D.
3.用加减消元法解方程组,下列做法正确的是( )
A.①+② B.①﹣② C.①+②×5 D.①×5﹣②
4.在等式y=kx+b中,当x=1时,y=﹣2;当x=﹣1时,y=﹣4.则2k+b的值为( )
A.1 B.﹣1 C.﹣2 D.﹣3
5.已知方程组的解满足x﹣y=3,则k的值为( )
A.﹣2 B.2 C.﹣1 D.1
6.已知是二元一次方程组的解,则4a﹣5b的平方根为( )
A. B.2 C.± D.±2
7.方程组的解为,则被△和▽遮盖的两个数分别为( )
A.﹣10,6 B.2,﹣6 C.2,6 D.10,﹣6
8.在解关于x、y的方程组时甲看错①中的a,解得x=4,y=2,乙看错②中的b,解得x=﹣3,y=﹣1,则a和b的正确值应是( )
A.a=﹣4.25,b=3 B.a=4,b=13
C.a=4,b=4 D.a=﹣5,b=4
9.成都大熊猫繁育研究基地是全国热门景点,某店家推出了纪念品礼盒深受国内外游客喜爱,一个礼盒里包含1个花花玩偶和3个花花钥匙扣.已知一个玩偶的进价为50元,一个钥匙扣的进价为10元,该店家计划用8000元购进一批玩偶和钥匙扣,使得刚好配套,设购进x个玩偶,y个钥匙扣,则下列方程组正确的是( )
A. B.
C. D.
10.把如图1的两张大小相同的长方形卡片放置在图2与图3中的两个相同大长方形中,已知这两个大长方形的长比宽长20cm,若记图2中阴影部分的周长为C1,图3中阴影部分的周长为C2,那么C1﹣C2=( )
A.10cm B.20cm C.30cm D.40cm
二.填空题(共6小题,满分24分,每小题4分)
11.已知方程5x+3y=1,改写成用含x的式子表示y的形式 .
12.解二元一次方程组时,小华用加减消元法消去未知数x,按照他的思路,用①﹣②得到的方程是 .
13.已知x与y的互为相反数,并且2x﹣y=3,则xy的值为 .
14.若关于x、y的方程组有整数解,则正整数a的值为 .
15.为宣传瑞安被推选为“2022中国最具幸福感城市”,政府计划制作两块长为36cm、宽为30cm的大长方形广告牌.广告牌内部有若干块形状大小完全相同的小长方形灯带,拼成了“瑞”、“安”两个字,则每块小长方形灯带的面积为 cm2.
16.已知关于x,y的二元一次方程ax+by=c的解如表:
x … ﹣4 ﹣3 ﹣2 ﹣1 0 1 …
y … 4 2 …
关于x,y的二元一次方程mx﹣ny=k的解如表:
x … ﹣4 ﹣3 ﹣2 ﹣1 0 1 …
y … 4 1 ﹣2 …
则关于x,y的二元一次方程组的解是 .
三.解答题(共7小题,满分66分)
17.(8分)解方程组:
(1); (2).
18.(6分)解方程组:.
19.(9分)如果某个二元一次方程组的解中两个未知数的值是互为相反数,我们称这个方程组为“关联方程组”.
(1)判断方程组是不是“关联方程组”,并说明理由;
(2)如果关于x,y的方程组是“关联方程组”,求a的值.
20.(9分)已知关于x,y的二元一次方程组与方程组有相同的解.
(1)求这两个方程组的相同解;
(2)求(2a+b)2024的值.
21.(10分)阅读以下材料:
解方程组:,小阳在解决这个问题时,发现了一种新的方法,他把这种方法叫做“整体代入法”,解题过程如下:
解:由①得x+y=1③,将③代入②得:
(1)请你替小阳补全完整的解题过程;
(2)请你用这种方法解方程组:.
22.(12分)某体育用品商场销售A,B两款足球,售价和进价如表:
类型 进价(元/个) 售价(元/个)
A款 m 120
B款 n 90
若该商场购进5个A款足球和12个B款足球需1120元;若该商场购进10个A款足球和15个B款足球需1700元.
(1)求m和n的值;
(2)某校在该商场一次性购买A款足球x个和B款足球y个,共消费3300元,那么该商场可获利多少元?
(3)为了提高销量,商场实施:“买足球送跳绳”的促销活动:“买1个A款足球送1根跳绳,买3个B款足球送2根跳绳”,每根跳绳的成本为10元,某日售卖出两款足球总计盈利600元,那么该日商场销售A、B两款足球各多少个?(每款都有销售)
23.(12分)根据素材,完成任务.
如何设计雪花模型材料采购方案?
素材一 学校组织同学参与甲、乙两款雪花模型的制作.每款雪花模型都需要用到长、短两种管子材料.某同学用6根长管子、48根短管子制作了1个甲雪花模型与1个乙雪花模型.已知制作一个甲、乙款雪花模型需要的长、短管子数分别为1:7与1:9.
素材二 某商店的店内广告牌如图所示.5月,学校花费320元向该商店购得的长管子数量比花200元购得的短管子数量少80根. 1.短管子售价:a元/根,长管子售价:2a元/根2.6月1日起,购买3根长管子赠送1根短管子.3.本店库存数量有限,长管子仅剩267根,短管子仅剩2130根,先到先得!
素材三 6月,学校有活动经费1280元,欲向该商店采购长、短管子各若干根全部用来制作甲、乙雪花模型(材料没有剩余),且采购经费恰好用完.
问题解决
任务一 分析雪花模型结构 求制作一个甲、乙款雪花模型分别需要长、短管子多少根?
任务二 确定采购费用 试求a的值并求出假如6月只制作一个甲款雪花模型的材料采购费.
任务三 拟定采购方案 求出所有满足条件的采购方案,并指出哪种方案得到的雪花总数最多.
参考答案
一.选择题
1.解:∵|m﹣2|x+3y|m﹣1|=23是关于x,y的二元一次方程,
∴,
解得m=0.
故选:B.
2.解:A.当x=﹣2,y=﹣2,得x+2y=﹣6,那么x=﹣2,y=﹣2不是x+2y=6的解,故A不符合题意.
B.当x=0,y=2,得x+2y=4,那么x=0,y=2不是x+2y=6的解,故B不符合题意.
C.当x=2,y=2,得x+2y=2+4=6,那么x=2,y=2是x+2y=6的解,故C符合题意.
D.当x=3,y=1,得x+2y=3+2=5,那么x=3,y=1不是x+2y=6的解,故D不符合题意.
故选:C.
3.解:若消去y,
则①+②得:6x=﹣16;
若消去x,
则①﹣②×5得:﹣12y=98;
故选:A.
4.解:由题意可得,
①+②,得b=﹣3,
将b=﹣3代入①得,k=1,
∴2k+b=2﹣3=﹣1,
故选:B.
5.解:,
②﹣①,得:x﹣y=1﹣k,
∵x﹣y=3,
∴1﹣k=3,
解得:k=﹣2,
故选:A.
6.解:把代入二元一次方程组得:,
解得:,
4a﹣5b=12﹣10=2,
2的平方根为:.
故选:C.
7.解:∵方程组的解为,
∴﹣2﹣y=4,
解得:y=﹣6,
∴▽=﹣6,
∴Δ=2×(﹣2)﹣(﹣6)=2,
∴被△和▽遮盖的两个数分别为2,﹣6.
故选:B.
8.解:将x=4,y=2代入3x﹣by=4得12﹣2b=4,
解得:b=4,
将x=﹣3,y=﹣1代入ax+8y=7得﹣3a﹣8=7,
解得:a=﹣5,
故选:D.
9.解:∵一个礼盒里包含1个花花玩偶和3个花花钥匙扣,且购进的偶和钥匙扣刚好配套,
∴3x=y;
∵该店家计划用8000元购进一批玩偶和钥匙扣,且一个玩偶的进价为50元,一个钥匙扣的进价为10元,
∴50x+10y=8000.
∴根据题意可列方程组.
故选:C.
10.解:设大长方形的宽为a cm,则长为(a+20)cm,图①中的长方形长为x cm,宽为y cm,
图②中阴影部分的周长C1为:2[(a+20)+a]=(4a+40)cm,
由图③可得,x+y=a+20,
图③中阴影部分的周长C2为:2(a+20)+2(a﹣y)+2(a﹣x)=2(3a+20﹣x﹣y)=2(3a+20﹣a﹣20)=4a(cm),
C1﹣C2=(4a+40)﹣4a
=4a+40﹣4a
=40(cm).
故选:D.
二.填空题
11.解:5x+3y=1,
3y=1﹣5x,
y=.
故答案为:y=.
12.解:解二元一次方程组时,小华用加减消元法消去未知数x,按照他的思路,用①﹣②得到的方程是:4y=﹣3,
故答案为:4y=﹣3.
13.解:∵x与y互为相反数,
∴x+y=0,
∴,
①+②,得3x=3,
解得x=1,
∴y=﹣1,
∴xy=1﹣1=1.
故答案为:1.
14.解:,
由②得:③,
把③代入①得:,
把代入③得:,
∵关于x、y的方程组有整数解,
∴a﹣2=±1或±3或±9,2﹣a=±1或±2或±3或±6,
解得:a=±1或3或5,
∴正整数a的值为:1或3或5.
故答案为:1或3或5.
15.解:设每块小长方形灯带的长为x cm,宽为y cm,
由题意得:,
解得:,
∴xy=9×3=27,
即每块小长方形灯带的面积为27cm2,
故答案为:27.
16.解:由表可得:的解为:,
∴二元一次方程组的解为:,
解得:,
故答案为:.
三.解答题
17.解:(1),
将②代入①得:2(y+1)+3y=22,
整理得:5y+2=22,
解得:y=4,
将y=4代入②得:x=4+1=5,
故原方程组的解为;
(2),
①×2+②得:8x=18,
解得:x=,
将x=代入②得:﹣4y=4,
解得:y=,
故原方程组的解为.
18.解:,
②+③得:
3x+y=﹣1④,
④×3得:
9x+3y=﹣3⑤,
⑤﹣①得:
7x=﹣7,
解得:x=﹣1,
把x=﹣1代入①得:
﹣2+3y=4,
解得:y=2,
把x=﹣1,y=2代入②得:
﹣2﹣2+2z=﹣4,
解得:z=0,
∴原方程组的解为:.
19.解:(1)方程组是“关联方程组”,理由如下:
,
(①﹣②)÷2得:x+y=0,
∴方程组是“关联方程组”;
(2),
(①+②)÷2得:x+y=2+a.
又∵关于x,y的方程组是“关联方程组”,
∴x+y=2+a=0,
解得:a=﹣2,
∴a的值为﹣2.
20.解:(1)由题意,得,
①+②,得5x=10,解得x=2.
把x=2代入①,得4+5y=﹣26,解得y=﹣6.
∴这两个方程组的相同解为
(2)把代入得:
解此方程组,
得a=1,b=﹣1,
∴(2a+b)2024=(2﹣1)2024=1.
21.解:(1)由①得x+y=1③,
将③代入②得3×1+y=2,
解得y=﹣1,
把y=﹣1代入①得,
x﹣1﹣1=0,
解得x=2,
故原方程组的解是;
(2)整理得,
,
把①代入②得,
2×(﹣1)+2+6y=12,
解得y=2,
把y=2代入①得,
3x﹣2=﹣1,
解得x=,
故原方程组的解是.
22.解:(1)根据题意得:,
解得:,
∴m的值为80,n的值为60;
(2)根据题意得:120x+90y=3300,
∴40x+30y=1100,
∴(120﹣80)x+(90﹣60)y=40x+30y=1100.
答:该商场可获利1100元;
(3)设该日商场销售a个A款足球,3b个B款足球,
根据题意得:(120﹣80﹣10)a+(90×3﹣60×3﹣10×2)b=600,
∴a=20﹣b,
又∵a,b均为正整数,
∴或,
∴或.
答:该日商场销售13个A款足球、9个B款足球或6个A款足球、18个B款足球.
23.任务一:假设制作一个甲乙款雪花模型分别需要长管子的个数为x,y,则需要短管为7x,9y,
则,
解得,
所以制作甲乙款雪花模型分别需要长管子的个数分别为3,3,短管子的个数为21,27.
任务二:由题意得,
解得:a=,
3×l+(21﹣1)×=13(元);
任务三:假设制作甲款雪花模型m个,乙款n个则需要长管子(3m+3n)个,短管子(21m+2m)个,
由题意可得:(3m+3n)(21m+27n﹣)=1280,
化简得到13m+16n=1280,
解得:,,,,
显然 0+40<16+27<32+14<48+1,
对应的采购方案为:
(1)长管购买1201,赠40短管,购买短管1080个,
(2)长管购买1299,赠43管,购买短管1065个,
(3)长管购买138个,赠46管购买短管1050个,
(4)长管购买147T赠49管购买短管1035个,
其中方案(4)雪花总数最多,为49个.
