第九章 图形的相似专题4 巧用位似解三角形中的内接多边形问题(含答案)
文档属性
| 名称 | 第九章 图形的相似专题4 巧用位似解三角形中的内接多边形问题(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-31 09:39:00 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
第九章 图形的相似
专题4 巧用位似解三角形中的内接多边形问题
类型1 三角形的内接正三角形问题
1.如图,用下面的方法可以画 的内接等边三角形,阅读后证明相应问题.
画法:(1)在 内画等边三角形CDE,使点C 在OA上,点D在OB上;(2)连接OE 并
延长,交AB 于点. 过点. 作 ∥交OA 于点 作 ∥交 OB 于点
(3)连接 则 是 的内接等边三角形.
求证: 是等边三角形.
类型2 三角形的内接矩形问题
2.如图,求作:内接于 的矩形DEFG,使它的边 EF 在 BC 上,顶点 D,G 分别在AB,AC上,并且有 DE :EF=1:2.
类型3 三角形的内接正方形问题(方程思想)
3.如图, 是一块锐角三角形余料,边 120 mm,高要把它加工成正方形零件 PQMN,使正方形 PQMN的一边 QM 在BC 上,其余两个顶点 P,N分别在AB,AC 上,
则这个正方形零件的边长是多少
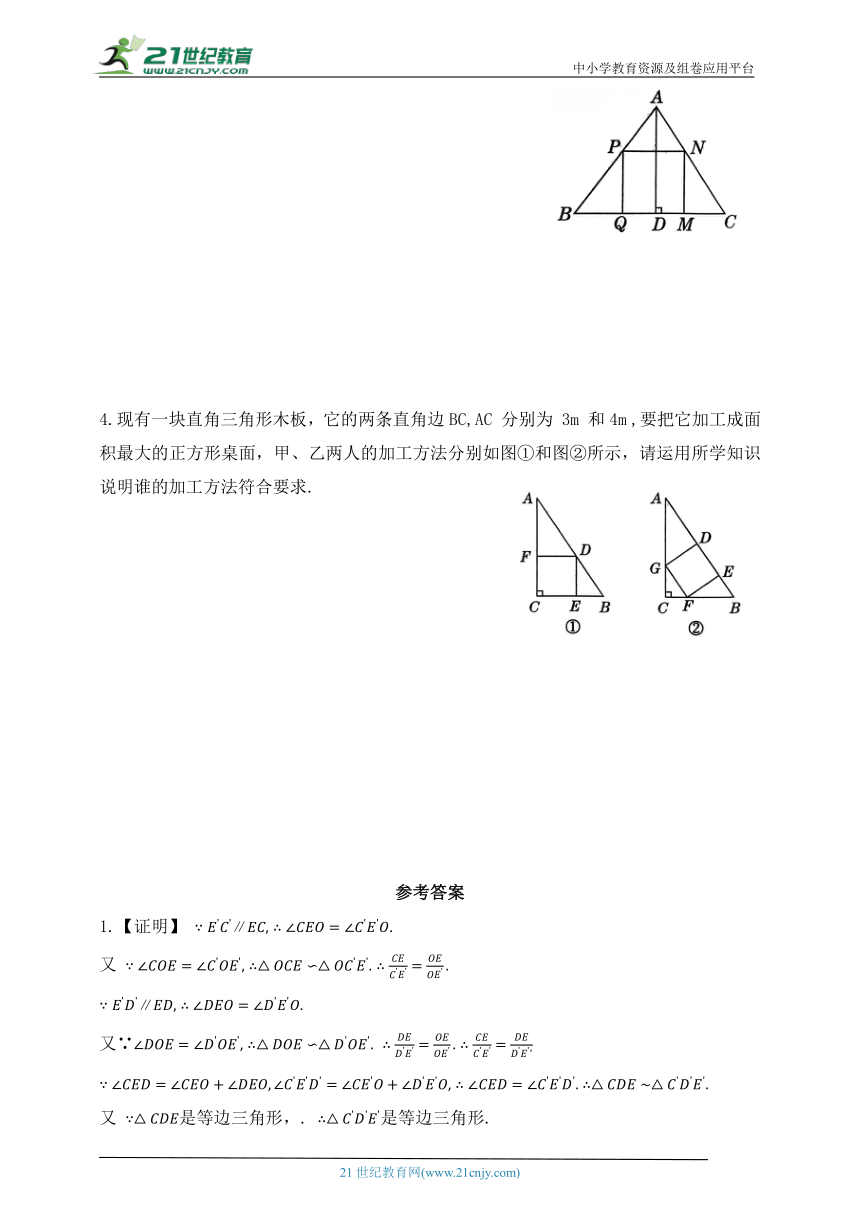
4.现有一块直角三角形木板,它的两条直角边BC,AC 分别为 3m 和4m ,要把它加工成面积最大的正方形桌面,甲、乙两人的加工方法分别如图①和图②所示,请运用所学知识说明谁的加工方法符合要求.
参考答案
1.【证明】 ∥
又
∥
又∵
又 是等边三角形,. 是等边三角形.
2.【解】如图,在 AB 上任取一点过点 作 于点在BC上截取 使 过点 作 过点 作 ∥交于点 作射线 交 AC 于点 G,过点 G 作∥∥GF 交BC于点F,DG交AB于点 D,过点D作∥交 BC 于点E,则四边形DEFG为 的内接矩形,且
3.【解】设 PN与AD 相交于点 E,正方形PQMN的边长为 x mm,易知 AE 为△APN 的边 PN上的高,ED=x mm.
∵ PN∥BC,∴∠APN = ∠B,∠ANP =
即 解得 x =48,即这个正方形零件的边长是48 mm.
4.【解】设甲加工的桌面边长为 x m.
由 FD∥BC,易得△AFD∽△ACB.即 解得 x =
设乙加工的桌面边长为 ym,如图,过点C 作CM⊥AB,垂足为M,CM交GF 于点N,
易得 NM=y m,CN⊥GF. 在Rt△ABC 中,BC=3m ,
由GF∥AB,易得△GCF∽△ACB.即 解得
甲加工的桌面面积最大,∴甲的加工方法符合要求.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第九章 图形的相似
专题4 巧用位似解三角形中的内接多边形问题
类型1 三角形的内接正三角形问题
1.如图,用下面的方法可以画 的内接等边三角形,阅读后证明相应问题.
画法:(1)在 内画等边三角形CDE,使点C 在OA上,点D在OB上;(2)连接OE 并
延长,交AB 于点. 过点. 作 ∥交OA 于点 作 ∥交 OB 于点
(3)连接 则 是 的内接等边三角形.
求证: 是等边三角形.
类型2 三角形的内接矩形问题
2.如图,求作:内接于 的矩形DEFG,使它的边 EF 在 BC 上,顶点 D,G 分别在AB,AC上,并且有 DE :EF=1:2.
类型3 三角形的内接正方形问题(方程思想)
3.如图, 是一块锐角三角形余料,边 120 mm,高要把它加工成正方形零件 PQMN,使正方形 PQMN的一边 QM 在BC 上,其余两个顶点 P,N分别在AB,AC 上,
则这个正方形零件的边长是多少
4.现有一块直角三角形木板,它的两条直角边BC,AC 分别为 3m 和4m ,要把它加工成面积最大的正方形桌面,甲、乙两人的加工方法分别如图①和图②所示,请运用所学知识说明谁的加工方法符合要求.
参考答案
1.【证明】 ∥
又
∥
又∵
又 是等边三角形,. 是等边三角形.
2.【解】如图,在 AB 上任取一点过点 作 于点在BC上截取 使 过点 作 过点 作 ∥交于点 作射线 交 AC 于点 G,过点 G 作∥∥GF 交BC于点F,DG交AB于点 D,过点D作∥交 BC 于点E,则四边形DEFG为 的内接矩形,且
3.【解】设 PN与AD 相交于点 E,正方形PQMN的边长为 x mm,易知 AE 为△APN 的边 PN上的高,ED=x mm.
∵ PN∥BC,∴∠APN = ∠B,∠ANP =
即 解得 x =48,即这个正方形零件的边长是48 mm.
4.【解】设甲加工的桌面边长为 x m.
由 FD∥BC,易得△AFD∽△ACB.即 解得 x =
设乙加工的桌面边长为 ym,如图,过点C 作CM⊥AB,垂足为M,CM交GF 于点N,
易得 NM=y m,CN⊥GF. 在Rt△ABC 中,BC=3m ,
由GF∥AB,易得△GCF∽△ACB.即 解得
甲加工的桌面面积最大,∴甲的加工方法符合要求.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
