五四制鲁教版八年级下册期末测试数学题(含答案)
文档属性
| 名称 | 五四制鲁教版八年级下册期末测试数学题(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 5.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-31 09:43:27 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
五四制鲁教版八年级数学下册期末测试题
(120 分 90 分钟)
一、选择题(每题3分,共36分)
1. 若 则 等于( )
A. B. C. D.
2.如表是代数式 的值的情况,根据表格中的数据,可知方程 的根是( )
… -3 -2 -1 0 1 2 3 4 …
… 12 6 2 0 0 2 6 12 …
3.用配方法解方程 时, 方程可变形为( )
4.如图,将长方形和直角三角形的直角顶点重合,若∠AOE=128°,则∠COD的度数为( )
A.28° B.38° C.52°
5.下列各式与 是同类二次根式的是( )
6.如图,已知 若AB 的长度为6,则 DE 的长度为( )
A.4 B.9 C.12 D.13.5
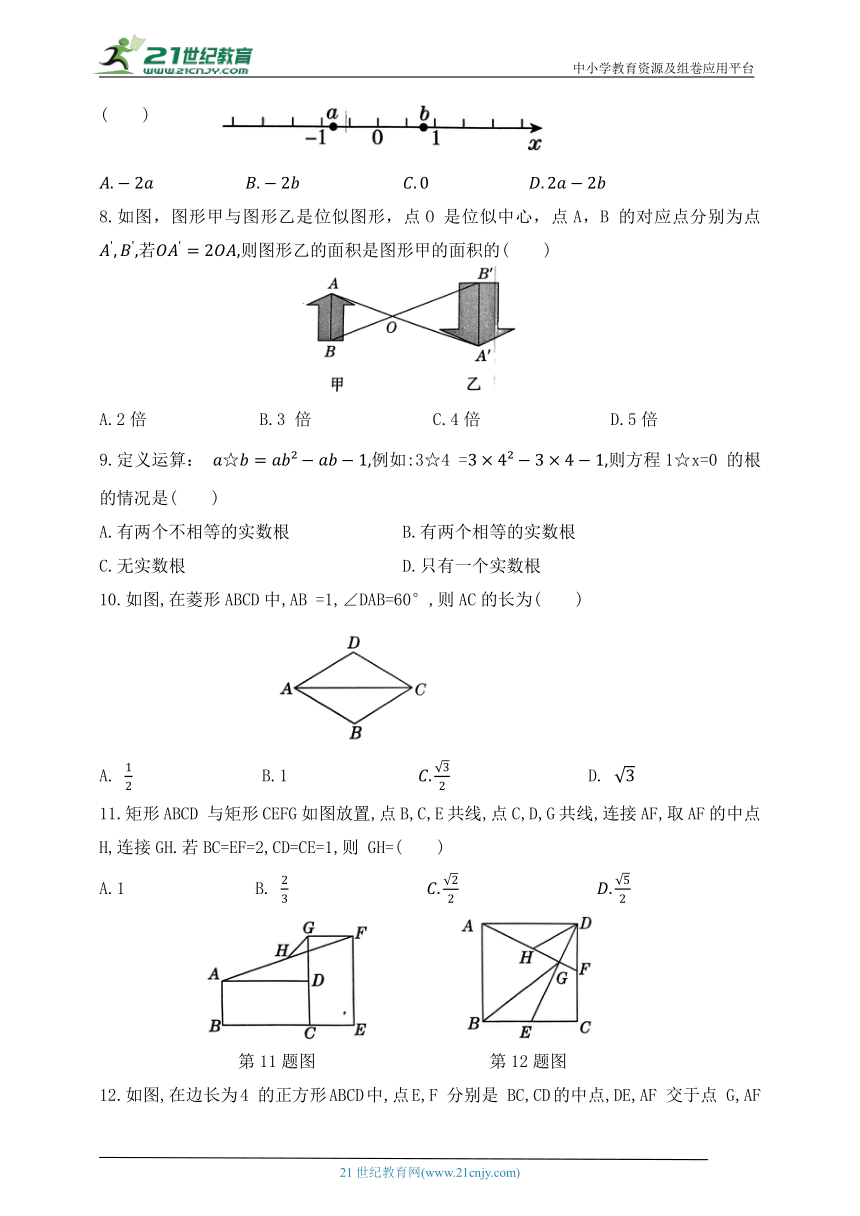
7.表示实数a,b的点在数轴上的位置如图所示,化简 的结果是( )
8.如图,图形甲与图形乙是位似图形,点O 是位似中心,点A,B 的对应点分别为点若则图形乙的面积是图形甲的面积的( )
A.2倍 B.3 倍 C.4倍 D.5倍
9.定义运算: 例如:3☆4 =则方程1☆x=0 的根的情况是( )
A.有两个不相等的实数根 B.有两个相等的实数根
C.无实数根 D.只有一个实数根
10.如图,在菱形ABCD中,AB =1,∠DAB=60°,则AC的长为( )
A. B.1 D.
11.矩形ABCD 与矩形CEFG如图放置,点B,C,E共线,点C,D,G共线,连接AF,取AF的中点H,连接GH.若BC=EF=2,CD=CE=1,则 GH=( )
A.1 B.
第11题图 第12题图
12.如图,在边长为4 的正方形ABCD中,点E,F 分别是 BC,CD的中点,DE,AF 交于点 G,AF 的中点为H,连接BG,DH.给出下列结论:①AF②③∥BG;④△ABG与△DHF 相似.其中正确的结论有( )
A.1 个 B.2 个 C.3 个 D.4个
二、填空题(每题3 分,共18分)
13.若二次根式 有意义,则 x 的取值范围是____________.
14.若 则
15.若关于x的一元二次方程( 有实数根,则k的取值范围为______________.
16.如图,等边三角形 ABC 被矩形DEFG所截,EF∥BC,线段 AB 被截成三等份.若△ABC
的面积为12 cm ,图中阴影部分的面积为____________
第16题图 第17题图 第18题图
17.如图,在平面直角坐标系中,点A 的坐标为(9,0),点C的坐标为(0,3),以OA,OC 为边作矩形OABC.动点E,F 分别从点 O,B 同时出发,以每秒1 个单位长度的速度沿 OA,BC 向终点 A,C 移动. 当移动时间为4 秒时,AC·EF 的值为____________.
18.如图,边长为2 的正方形ABCD中,E,F分别是边BC,CD 的中点,连接 AE,G 是 AE 上的一点,则GF=____________.
三、解答题(19~21 题每题8分,22~24 题每题10 分,25 题12分,共66分)
19.计算:
20.解下列方程:
21.已知关于x的一元二次方程 有实根,方程的两个实数根分别为 ,若 求k的值.
22.如图,在平面直角坐标系中,菱形OABC 的一边OC 在x 轴正半轴上,顶点 A的坐标为(2,点D 是边 OC 上的动点,过点D作交边OA 于点E,作 ∥交边BC 于点F,连接EF,设x, 的面积为 S.
(1)用x 表示线段 DF.
(2)求 S关于x的函数表达式.
23.为了加快发展新能源和清洁能源,助力实现“双碳”目标,大力发展高效光伏发电关键零部件制造.青岛上合示范区某工厂生产的某种零件按供需要求分为8 个档次.若生产第一档次(最低档次)的产品,一天可生产38 件,每件的利润为 12元,每提高一个档次,每件的利润增加3元,每天的产量将减少2 件. 请解答下列问题,设产品的档次(每天只生产一个档次的产品)为x,若该产品一天的总利润为756元,求这天生产产品的档次x的值.
24.如图,已知矩形 ABCD,点E 在 CB的延长线上,点 F 在BC的延长线上,过点 F 作. 交 ED的延长线于点 H,连接AF 交 EH 于点G,
(1)求证:
(2)当 时,求EF 的长.
25.如图,在边长为1 的正方形ABCD 中,点 E 在边AD上(不与点A,D重合),射线 BE 与射线 CD 交于点 F.
(1)若 求 DF 的长.
(2)求证:
(3)以点 B为圆心,BC 长为半径画弧,交线段 BE 于点 G.若求ED的长.
参考答案
一、1. D 【点拨】
2. D 【点拨】由表中数据得,当 时, 12;当时, 所以方程 的解为
3. D 【点拨】
4. C 【点拨】∵ 将长方形和直角三角形的直角顶点O重合,
5. C 【点拨】·
∴ 与 是同类二次根式的是
6. B 【点拨】·
当 时,
7. A 【点拨】由数轴可知
∴ 原式
8. C 【点拨】由题意可得,甲乙两图形相似,且相似比为 根据相似图形的面积比是相似比的平方可得,图形乙的面积是图形甲的面积的4 倍.
9. A
10. D 【点拨】如图,连接 BD 交AC 于点 O.
∵ 四边形 ABCD 是菱形,
11. C 【点拨】如图,延长GH 交AD 于点 P.
∵ 四边形 ABCD和四边形CEFG都是矩形,∴∠ADC = ∠ADG =∠CGF =∥∴∠GFH=∠PAH. 又∵H是 AF 的中点,∴AH=FH,
在△APH和△FGH中.
12. B 【点拨】∵四边形ABCD为正方形,∴∠ADC=∠BCD=90°,AD=CD.∵E 和 F 分别为 BC 和CD的中点,∴ DF = EC,∴△ADF≌△DCE(SAS),∴∠AFD=∠DEC,∠FAD =∠EDC.
∵ ∠EDC +即 故①正确; 又 故②错误;∵H为 AF 的中点, 故④正确;由④可知和 不相等,∴∠AGB≠∠DHF,∴HD 与BG不平行,故③错误.综上所述①④正确.
二、13. x≥3 【点拨】根据题意,得: 解得
14.13 【点拨】设 则
且 【点拨】∵关于x的一元二次方程 有实数根, 解得 且k≠2.
16.4 【点拨】易知
又易知△∴ 图中阴影部分的面积为
17.30 【点拨】如图, 连接AC,EF,则∵四边形OABC 为 矩形,∴B(9,3).
又
【点拨】如图,连接BF,交 AE 于点H.
∵ 四边形 ABCD 是正方形,∴
∵点 E,F 分别是边 BC,CD的中点,∴BE=CF,
在 与 中,∴△ABE≌△BCF(SAS),
是等腰直角三角形,
三、19.【解】
20.【解】 或
即
21.【解】∵关于x的一元二次方程 有实根,
解得
∵方程的两个实数根分别为
∵
解得
符合题意. 故所求 k 的值为
22.【解】(1)如图,过点 A 作 于点 G,连接 AC.
∵顶点 A 的坐标为(
∵四边形 OABC 是菱形,
∴△AOC 是等边三角形,
∵DE⊥OB,∴DE∥AC,∴∠EDO=∠ACO=60°,∴△EOD是等边三角形,∴ED=OD=x.
23.【解】∵该工厂生产产品的档次(每天只生产一个档次的产品)为x,∴每件产品的利润为 元,一天可生产 2x)件产品.
根据题意得( 整理得 解得 (不符合题意,舍去). ∴ 这天生产产品的档次 x 的值为6.
24.(1)【证明】∵ HF⊥EF,∴∠HFE=90°.
∵四边形ABCD 是矩形,∴AB=DC,∠ABC=∠DCB=90°,∴△ABF≌△DCE(AAS),
∴BF=CE,∴BF-BC=CE-BC,即BE=CF.
(2)【解】∵ 四边形ABCD 是矩形,∴BC=AD=4.
∵∠HFE=∠DCB=90°,∠HEF=∠DEC, .
设BE=CF=x,则EC=x+4, 解得 x=1,∴EF=6.
25.(1)【解】∵ 四边形ABCD是正方形,∴AD∥BC,AB=AD=BC=CD=1,
∴∠DEF=∠CBF,∠EDF=∠BCF,∴△DEF∽△CBF,
(2)【证明】∵AB∥CD,∴∠ABE=∠F.
又∵∠A=∠BCD=90°,∴△ABE∽△CFB,
(3)【解】设EG=ED=x,则AE=AD-ED=1-x,BE =BG+GE=BC +GE=1 +x.
在 Rt△ABE中,
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
五四制鲁教版八年级数学下册期末测试题
(120 分 90 分钟)
一、选择题(每题3分,共36分)
1. 若 则 等于( )
A. B. C. D.
2.如表是代数式 的值的情况,根据表格中的数据,可知方程 的根是( )
… -3 -2 -1 0 1 2 3 4 …
… 12 6 2 0 0 2 6 12 …
3.用配方法解方程 时, 方程可变形为( )
4.如图,将长方形和直角三角形的直角顶点重合,若∠AOE=128°,则∠COD的度数为( )
A.28° B.38° C.52°
5.下列各式与 是同类二次根式的是( )
6.如图,已知 若AB 的长度为6,则 DE 的长度为( )
A.4 B.9 C.12 D.13.5
7.表示实数a,b的点在数轴上的位置如图所示,化简 的结果是( )
8.如图,图形甲与图形乙是位似图形,点O 是位似中心,点A,B 的对应点分别为点若则图形乙的面积是图形甲的面积的( )
A.2倍 B.3 倍 C.4倍 D.5倍
9.定义运算: 例如:3☆4 =则方程1☆x=0 的根的情况是( )
A.有两个不相等的实数根 B.有两个相等的实数根
C.无实数根 D.只有一个实数根
10.如图,在菱形ABCD中,AB =1,∠DAB=60°,则AC的长为( )
A. B.1 D.
11.矩形ABCD 与矩形CEFG如图放置,点B,C,E共线,点C,D,G共线,连接AF,取AF的中点H,连接GH.若BC=EF=2,CD=CE=1,则 GH=( )
A.1 B.
第11题图 第12题图
12.如图,在边长为4 的正方形ABCD中,点E,F 分别是 BC,CD的中点,DE,AF 交于点 G,AF 的中点为H,连接BG,DH.给出下列结论:①AF②③∥BG;④△ABG与△DHF 相似.其中正确的结论有( )
A.1 个 B.2 个 C.3 个 D.4个
二、填空题(每题3 分,共18分)
13.若二次根式 有意义,则 x 的取值范围是____________.
14.若 则
15.若关于x的一元二次方程( 有实数根,则k的取值范围为______________.
16.如图,等边三角形 ABC 被矩形DEFG所截,EF∥BC,线段 AB 被截成三等份.若△ABC
的面积为12 cm ,图中阴影部分的面积为____________
第16题图 第17题图 第18题图
17.如图,在平面直角坐标系中,点A 的坐标为(9,0),点C的坐标为(0,3),以OA,OC 为边作矩形OABC.动点E,F 分别从点 O,B 同时出发,以每秒1 个单位长度的速度沿 OA,BC 向终点 A,C 移动. 当移动时间为4 秒时,AC·EF 的值为____________.
18.如图,边长为2 的正方形ABCD中,E,F分别是边BC,CD 的中点,连接 AE,G 是 AE 上的一点,则GF=____________.
三、解答题(19~21 题每题8分,22~24 题每题10 分,25 题12分,共66分)
19.计算:
20.解下列方程:
21.已知关于x的一元二次方程 有实根,方程的两个实数根分别为 ,若 求k的值.
22.如图,在平面直角坐标系中,菱形OABC 的一边OC 在x 轴正半轴上,顶点 A的坐标为(2,点D 是边 OC 上的动点,过点D作交边OA 于点E,作 ∥交边BC 于点F,连接EF,设x, 的面积为 S.
(1)用x 表示线段 DF.
(2)求 S关于x的函数表达式.
23.为了加快发展新能源和清洁能源,助力实现“双碳”目标,大力发展高效光伏发电关键零部件制造.青岛上合示范区某工厂生产的某种零件按供需要求分为8 个档次.若生产第一档次(最低档次)的产品,一天可生产38 件,每件的利润为 12元,每提高一个档次,每件的利润增加3元,每天的产量将减少2 件. 请解答下列问题,设产品的档次(每天只生产一个档次的产品)为x,若该产品一天的总利润为756元,求这天生产产品的档次x的值.
24.如图,已知矩形 ABCD,点E 在 CB的延长线上,点 F 在BC的延长线上,过点 F 作. 交 ED的延长线于点 H,连接AF 交 EH 于点G,
(1)求证:
(2)当 时,求EF 的长.
25.如图,在边长为1 的正方形ABCD 中,点 E 在边AD上(不与点A,D重合),射线 BE 与射线 CD 交于点 F.
(1)若 求 DF 的长.
(2)求证:
(3)以点 B为圆心,BC 长为半径画弧,交线段 BE 于点 G.若求ED的长.
参考答案
一、1. D 【点拨】
2. D 【点拨】由表中数据得,当 时, 12;当时, 所以方程 的解为
3. D 【点拨】
4. C 【点拨】∵ 将长方形和直角三角形的直角顶点O重合,
5. C 【点拨】·
∴ 与 是同类二次根式的是
6. B 【点拨】·
当 时,
7. A 【点拨】由数轴可知
∴ 原式
8. C 【点拨】由题意可得,甲乙两图形相似,且相似比为 根据相似图形的面积比是相似比的平方可得,图形乙的面积是图形甲的面积的4 倍.
9. A
10. D 【点拨】如图,连接 BD 交AC 于点 O.
∵ 四边形 ABCD 是菱形,
11. C 【点拨】如图,延长GH 交AD 于点 P.
∵ 四边形 ABCD和四边形CEFG都是矩形,∴∠ADC = ∠ADG =∠CGF =∥∴∠GFH=∠PAH. 又∵H是 AF 的中点,∴AH=FH,
在△APH和△FGH中.
12. B 【点拨】∵四边形ABCD为正方形,∴∠ADC=∠BCD=90°,AD=CD.∵E 和 F 分别为 BC 和CD的中点,∴ DF = EC,∴△ADF≌△DCE(SAS),∴∠AFD=∠DEC,∠FAD =∠EDC.
∵ ∠EDC +即 故①正确; 又 故②错误;∵H为 AF 的中点, 故④正确;由④可知和 不相等,∴∠AGB≠∠DHF,∴HD 与BG不平行,故③错误.综上所述①④正确.
二、13. x≥3 【点拨】根据题意,得: 解得
14.13 【点拨】设 则
且 【点拨】∵关于x的一元二次方程 有实数根, 解得 且k≠2.
16.4 【点拨】易知
又易知△∴ 图中阴影部分的面积为
17.30 【点拨】如图, 连接AC,EF,则∵四边形OABC 为 矩形,∴B(9,3).
又
【点拨】如图,连接BF,交 AE 于点H.
∵ 四边形 ABCD 是正方形,∴
∵点 E,F 分别是边 BC,CD的中点,∴BE=CF,
在 与 中,∴△ABE≌△BCF(SAS),
是等腰直角三角形,
三、19.【解】
20.【解】 或
即
21.【解】∵关于x的一元二次方程 有实根,
解得
∵方程的两个实数根分别为
∵
解得
符合题意. 故所求 k 的值为
22.【解】(1)如图,过点 A 作 于点 G,连接 AC.
∵顶点 A 的坐标为(
∵四边形 OABC 是菱形,
∴△AOC 是等边三角形,
∵DE⊥OB,∴DE∥AC,∴∠EDO=∠ACO=60°,∴△EOD是等边三角形,∴ED=OD=x.
23.【解】∵该工厂生产产品的档次(每天只生产一个档次的产品)为x,∴每件产品的利润为 元,一天可生产 2x)件产品.
根据题意得( 整理得 解得 (不符合题意,舍去). ∴ 这天生产产品的档次 x 的值为6.
24.(1)【证明】∵ HF⊥EF,∴∠HFE=90°.
∵四边形ABCD 是矩形,∴AB=DC,∠ABC=∠DCB=90°,∴△ABF≌△DCE(AAS),
∴BF=CE,∴BF-BC=CE-BC,即BE=CF.
(2)【解】∵ 四边形ABCD 是矩形,∴BC=AD=4.
∵∠HFE=∠DCB=90°,∠HEF=∠DEC, .
设BE=CF=x,则EC=x+4, 解得 x=1,∴EF=6.
25.(1)【解】∵ 四边形ABCD是正方形,∴AD∥BC,AB=AD=BC=CD=1,
∴∠DEF=∠CBF,∠EDF=∠BCF,∴△DEF∽△CBF,
(2)【证明】∵AB∥CD,∴∠ABE=∠F.
又∵∠A=∠BCD=90°,∴△ABE∽△CFB,
(3)【解】设EG=ED=x,则AE=AD-ED=1-x,BE =BG+GE=BC +GE=1 +x.
在 Rt△ABE中,
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
