2022~2023学年福建龙岩高一上学期期中数学试卷(一级联盟(九校))(PDF版含解析)
文档属性
| 名称 | 2022~2023学年福建龙岩高一上学期期中数学试卷(一级联盟(九校))(PDF版含解析) |  | |
| 格式 | |||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-31 14:02:25 | ||
图片预览




文档简介
2022~2023学年福建龙岩高一上学期期中数学试卷(一级联盟(九校))
一、单选题(本大题共8小题,每小题5分,共40分)
1、设集合 , ,则 ( )
A.
B.
C.
D.
2、函数 的定义域是( )
A.
B.
C.
D.
3、设命题p: , ,则 为
A. ,
B. ,
C. ,
D. ,
4、设 ,则“ ”是“ ”的
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件
5、关于x的不等式 的解集是( )
A.
B.
C.
D.
6、已知 , , ,则a,b,c的大小关系为( )
A.
B.
C.
D.
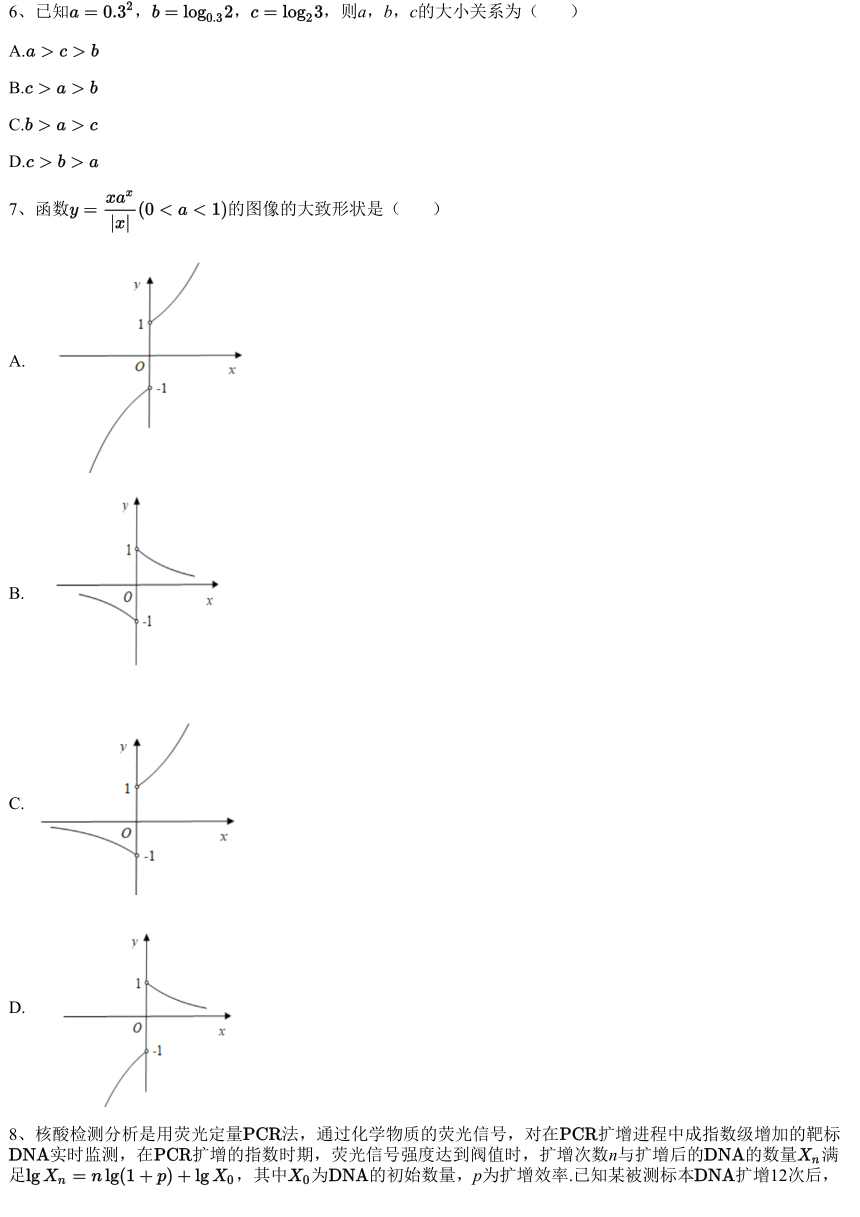
7、函数 的图像的大致形状是( )
A.
B.
C.
D.
8、核酸检测分析是用荧光定量 法,通过化学物质的荧光信号,对在 扩增进程中成指数级增加的靶标
实时监测,在 扩增的指数时期,荧光信号强度达到阀值时,扩增次数n与扩增后的 的数量 满
足 ,其中 为 的初始数量,p为扩增效率.已知某被测标本 扩增12次后,
数量变为原来的1000倍,则被测标本的 扩增13次后,数量变为原来的(参考数据: ,
, )( )
A.1334倍
B.1585倍
C.1778倍
D.5620倍
二、多选题(本大题共4小题,每小题5分,共20分)
9、若 ,则下列不等式一定成立的是( )
A.
B.
C.
D.
10、若“ , ”为假命题,则m的值可能为( )
A.0
B.
C.1
D.4
11、已知 是定义在 上的奇函数,当 时, ,则下列说法正确的是( ).
A.
B. 在定义域 上为增函数
C.当 时,
D.不等式 的解集为
12、欧拉对函数的发展做出了巨大贡献,除特殊符号、概念名称的界定外,欧拉还基于初等函数研究了抽象函
数的性质,例如,欧拉引入倒函数的定义:对于函数 ,如果对于其定义域D中任意给定的实数x,都有
,并且 ,就称函数 为倒函数,则下列函数是倒函数的为( )
A.
B.
C.
D.
三、填空题(本大题共4小题,每小题5分,共20分)
13、 .
14、函数 的图像恒过的定点是 .
15、若 , ,且 ,则 的最小值为 .
16、已知函数 ,若存在 , ,且 ,使得 成立,则实数
m的取值范围是 .
四、解答题(本大题共6小题,共70分)
17、(本小题10分)
设全集U , , .求 , ,
U U .
18、(本小题12分)
已知函数 .
(1) 若关于x的不等式 的解集为 或 ,求实数m,n的值;
(2)从以下两个条件① ,② 中选择一个作为条件,求关于x 的不等式 的解集.
(注:选择两个条件分别解答,按第一个解答计分)
19、(本小题12分)
已知幂函数 是定义在R上的偶函数.
(1)求 的解析式;
(2)在区间 上, 的图象总在函数 图象的上方,求实数k的取值范围.
20、(本小题12分)
“绿水青山就是金山银山”,将生态治理和发展特色产业有机结合起来,就可走出一条生态和经济协调发展、人
与自然和谐共生之路.若今年市财政预下拨专款100百万元,分别用于生态治理和发展特殊产业两个项目,生态
治理项目五年内带来的生态收益 (单位:百万元)与其投放资金x(单位:百万元)呈正比例函数关系,且投
放资金8百万元时可收益0.8百万元,发展特色产业项目五年内带来的产业收益 (单位:百万元)与其投放资
金x(单位:百万元)的函数关系是 .
(1)设分配给发展特色产业项目的资金为x(单位:百万元),两个项目五年内带来的收益总和为y(单位:百万
元),试将y表示成关于x的函数.
(2)对两个项目的投放资金如何分 配,可使收益总和达到最大?最大值是多少?
21、(本小题12分)
已知函数 是奇函数.
(1)求实数m的值;
(2) , , ,求实数c的取值范围.
22、(本小题12分)
已知实数 ,且函数 , ,
, , ,当 时,
的最小值记为 .
(1)若 ,求函数 的单调递减区间;
(2) , , ,求实数m的取值范围.
参考答案
一、单选题
1、
【答 案】
A
【分析】
通过题意分析可以得 ,所以 .
因此正确答案为:A.
2、
【答 案】
C
【分析】
解:对于函数 ,令 ,解得 且 ,
所以函数的定义域为 .
因此正确答案为:C
3、
【答 案】
B
【分析】
根据命题的否定的定义可知 : , .故选:B.
4、
【答 案】
A
【分析】
由 ,可得 或 ,∴“ ”是“ ”的充分不必要条件,故选:A.
5、
【答 案】
C
【分析】
因为 为减函数,所以 ,
解得 .
因此正确答案为:C
6、
【答 案】
B
【分析】
因为 为减函数,所以 ,所以 ,
因为 为减函数, ,所以 ,
因为 为增函数, ,所以 .
所以 .
因此正确答案为 :B
7、
【答 案】
D
【分析】
根据
,
是减函 数, 是增函数.
在 , 上单调递减,在 , 上单调递增
因此正确答案为:D.
8、
【答 案】
C
【分析】
通过题意分析可以得 ,
即 ,
解得 ,
所以 ,即 ,
解得 ,
因此正确答案为:C.
二、多选题
9、
【答 案】
A;C;D
【分析】
因为 ,对A, 为减函数,所以 ,A无误;
对B, ,则 ,故B有误;
对C, ,因为 ,所以同时除以 有 ,故C无误;
对D,因为 ,所以 ,又 ,所以 ,对数函数 为增函数,
所以 ,D无误.
因此正确答案为:ACD
10、
【答 案】
A;C
【分析】
因为若“ , ”为假命题,所以若“ , ”为真命题,当 时
显然成立;当 时,满足 ,解得 ,
故当 或1时都满足.
因此正确答案为:AC
11、
【答 案】
A;B;D
【分析】
因为 是定义域为 的奇函数,
所以 ,且 ,
当 时, ,
令 ,则 ,有 ,
所以 ,故C错误;
故 ,
所以 ,故A正确;
函数 的图象如图所示,
所以 是定义域为 的增函数,故B正确;
不等式 转化为 ,则 ,解得 ,
故D正确.
故选ABD.
12、
【答案 】
B;D
【分析】
对 , ,定义域不关于原点对称,故A项不符合;
对 , , ,故B项符合;
对 , ,定义域不关于原点对称,故C项不符合;
对 ,定义域关于原点对称,
当 时, , ;
当 时, , ,故D项符合,
因此正确答案为:BD
三、填空题
13、
【答 案】
1
【分析】
原式 .
因此正确答案为:1.
14、
【答案 】
【分析】
由 得 ,所以 ,故图象恒过定点为 ,因此正确答案为 .
15、
【答 案】
4
【分析】
由题设,知: 当且仅当 时等号成立.
因此正确答案为:4.
16、
【答案 】
【分析】
通过题意知,函数 在 上,存在 使得 成立,
则函数 在 上不单调.
,
若 , , ,
因为函数 和 在 上单调递减,
所以函数 在 上单调递减,与题意不相符;
若 , , ,
当 时,易知 在 上单调递减,有 ,
当 时, ,
则函数 在 上单调递 减,则 ,与题意不相符;
当 时, , ,
对于对勾函数 ,在 上和 单调递减,在 和 上单调递增,
则函数 在 上单调递增,在 上单调递减,
且对于 ,使得 ,
所以存在 , 使得 成立,
所以 .即实数 的取值范围为 .
因此正确答案为: .
四、解答题
17、
【答 案】
, , U U
【分析】
U ,
, U ,
, U ,
由 ,得
, ,
. U U
18、
【答案 】
(1)
(2)答案见详解
【分析】
(1)因为 解集为 或 ,所以 ,解得 ;
(2)若选① ,则 ,
令 得 ,
当 时, 的解集为 ;
当 时, 的解为 ;
当 时, 的解为 ;
若选② ,则 ,令 得
当 时, 的解集为 ;
当 时, 的解集为 ;
当 时, 的解集为 .
19、
【答案 】
(1)
(2)
【分析】
(1)因为 是幂函数,所以 ,解得 或 ,又函数为偶函
数,故 , ;
(2)原题可等价转化为 对 恒成立,
当 时恒成立;
当 时,分离参数得 ,即 ,由对勾函数图象特点可知 在
上单减,故 ,所以 ;
当 时,分离参数得 ,由对勾函数图象特点可知 在 上单减,
,所以 ,
所以
20、
【答案 】
(1) ;
(2)投资生态治理项目资金为5百万元,投资发展特色产业项目资金为95百万元时,总收益最大,且最大收益为
190.5百万元.
【分析】
(1)通过题意知,设 ,则 ,解得 ,所以 ,
所以 ,
即
(2)由(1),得
,
当且仅当 即 时,等号成立,
此时 ,
所以投资生态治理项 目资金为5百万元,投资发展特色产业项目资金为95百万元时,
总收益最大,且最大收益为190.5百万元.
21、
【答案 】
(1)
(2) 或
【分析】
(1)由 得 ,即 ,
因为奇函数的定义域关于原点对称,则必有 ,
此时 ,证明如下:
函数 是奇函数
(2)函数 在 上单调递增,
任取
则
,
又
,
即 ,
所以函数 在 上单调递增,
已知 , ,
所以 ,
又 ,
,
解得 或
22、
【答 案】
(1)
(2)
【分析】
(1)解:当 时, , ,
由 ,解得 ,
由 ,解得 或 ,
即 ,
,
,
当 时 ,函数在 上单调递增,在 上单调递减,
当 时 ,函数在 上单调递增,
故函数 的单调递减区间为 .
(2)解:令 ,
得 ,解得 或 ,
,解得 ,
,解得 或 ,
,
, ,
又因为函数 关于直线 对称,
故 ,
所以 ,
令 ,由 ,得 ,
由 ,有 成立,
可知 ,
故 ,
又 时, ,
所以 ,解得 .
一、单选题(本大题共8小题,每小题5分,共40分)
1、设集合 , ,则 ( )
A.
B.
C.
D.
2、函数 的定义域是( )
A.
B.
C.
D.
3、设命题p: , ,则 为
A. ,
B. ,
C. ,
D. ,
4、设 ,则“ ”是“ ”的
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件
5、关于x的不等式 的解集是( )
A.
B.
C.
D.
6、已知 , , ,则a,b,c的大小关系为( )
A.
B.
C.
D.
7、函数 的图像的大致形状是( )
A.
B.
C.
D.
8、核酸检测分析是用荧光定量 法,通过化学物质的荧光信号,对在 扩增进程中成指数级增加的靶标
实时监测,在 扩增的指数时期,荧光信号强度达到阀值时,扩增次数n与扩增后的 的数量 满
足 ,其中 为 的初始数量,p为扩增效率.已知某被测标本 扩增12次后,
数量变为原来的1000倍,则被测标本的 扩增13次后,数量变为原来的(参考数据: ,
, )( )
A.1334倍
B.1585倍
C.1778倍
D.5620倍
二、多选题(本大题共4小题,每小题5分,共20分)
9、若 ,则下列不等式一定成立的是( )
A.
B.
C.
D.
10、若“ , ”为假命题,则m的值可能为( )
A.0
B.
C.1
D.4
11、已知 是定义在 上的奇函数,当 时, ,则下列说法正确的是( ).
A.
B. 在定义域 上为增函数
C.当 时,
D.不等式 的解集为
12、欧拉对函数的发展做出了巨大贡献,除特殊符号、概念名称的界定外,欧拉还基于初等函数研究了抽象函
数的性质,例如,欧拉引入倒函数的定义:对于函数 ,如果对于其定义域D中任意给定的实数x,都有
,并且 ,就称函数 为倒函数,则下列函数是倒函数的为( )
A.
B.
C.
D.
三、填空题(本大题共4小题,每小题5分,共20分)
13、 .
14、函数 的图像恒过的定点是 .
15、若 , ,且 ,则 的最小值为 .
16、已知函数 ,若存在 , ,且 ,使得 成立,则实数
m的取值范围是 .
四、解答题(本大题共6小题,共70分)
17、(本小题10分)
设全集U , , .求 , ,
U U .
18、(本小题12分)
已知函数 .
(1) 若关于x的不等式 的解集为 或 ,求实数m,n的值;
(2)从以下两个条件① ,② 中选择一个作为条件,求关于x 的不等式 的解集.
(注:选择两个条件分别解答,按第一个解答计分)
19、(本小题12分)
已知幂函数 是定义在R上的偶函数.
(1)求 的解析式;
(2)在区间 上, 的图象总在函数 图象的上方,求实数k的取值范围.
20、(本小题12分)
“绿水青山就是金山银山”,将生态治理和发展特色产业有机结合起来,就可走出一条生态和经济协调发展、人
与自然和谐共生之路.若今年市财政预下拨专款100百万元,分别用于生态治理和发展特殊产业两个项目,生态
治理项目五年内带来的生态收益 (单位:百万元)与其投放资金x(单位:百万元)呈正比例函数关系,且投
放资金8百万元时可收益0.8百万元,发展特色产业项目五年内带来的产业收益 (单位:百万元)与其投放资
金x(单位:百万元)的函数关系是 .
(1)设分配给发展特色产业项目的资金为x(单位:百万元),两个项目五年内带来的收益总和为y(单位:百万
元),试将y表示成关于x的函数.
(2)对两个项目的投放资金如何分 配,可使收益总和达到最大?最大值是多少?
21、(本小题12分)
已知函数 是奇函数.
(1)求实数m的值;
(2) , , ,求实数c的取值范围.
22、(本小题12分)
已知实数 ,且函数 , ,
, , ,当 时,
的最小值记为 .
(1)若 ,求函数 的单调递减区间;
(2) , , ,求实数m的取值范围.
参考答案
一、单选题
1、
【答 案】
A
【分析】
通过题意分析可以得 ,所以 .
因此正确答案为:A.
2、
【答 案】
C
【分析】
解:对于函数 ,令 ,解得 且 ,
所以函数的定义域为 .
因此正确答案为:C
3、
【答 案】
B
【分析】
根据命题的否定的定义可知 : , .故选:B.
4、
【答 案】
A
【分析】
由 ,可得 或 ,∴“ ”是“ ”的充分不必要条件,故选:A.
5、
【答 案】
C
【分析】
因为 为减函数,所以 ,
解得 .
因此正确答案为:C
6、
【答 案】
B
【分析】
因为 为减函数,所以 ,所以 ,
因为 为减函数, ,所以 ,
因为 为增函数, ,所以 .
所以 .
因此正确答案为 :B
7、
【答 案】
D
【分析】
根据
,
是减函 数, 是增函数.
在 , 上单调递减,在 , 上单调递增
因此正确答案为:D.
8、
【答 案】
C
【分析】
通过题意分析可以得 ,
即 ,
解得 ,
所以 ,即 ,
解得 ,
因此正确答案为:C.
二、多选题
9、
【答 案】
A;C;D
【分析】
因为 ,对A, 为减函数,所以 ,A无误;
对B, ,则 ,故B有误;
对C, ,因为 ,所以同时除以 有 ,故C无误;
对D,因为 ,所以 ,又 ,所以 ,对数函数 为增函数,
所以 ,D无误.
因此正确答案为:ACD
10、
【答 案】
A;C
【分析】
因为若“ , ”为假命题,所以若“ , ”为真命题,当 时
显然成立;当 时,满足 ,解得 ,
故当 或1时都满足.
因此正确答案为:AC
11、
【答 案】
A;B;D
【分析】
因为 是定义域为 的奇函数,
所以 ,且 ,
当 时, ,
令 ,则 ,有 ,
所以 ,故C错误;
故 ,
所以 ,故A正确;
函数 的图象如图所示,
所以 是定义域为 的增函数,故B正确;
不等式 转化为 ,则 ,解得 ,
故D正确.
故选ABD.
12、
【答案 】
B;D
【分析】
对 , ,定义域不关于原点对称,故A项不符合;
对 , , ,故B项符合;
对 , ,定义域不关于原点对称,故C项不符合;
对 ,定义域关于原点对称,
当 时, , ;
当 时, , ,故D项符合,
因此正确答案为:BD
三、填空题
13、
【答 案】
1
【分析】
原式 .
因此正确答案为:1.
14、
【答案 】
【分析】
由 得 ,所以 ,故图象恒过定点为 ,因此正确答案为 .
15、
【答 案】
4
【分析】
由题设,知: 当且仅当 时等号成立.
因此正确答案为:4.
16、
【答案 】
【分析】
通过题意知,函数 在 上,存在 使得 成立,
则函数 在 上不单调.
,
若 , , ,
因为函数 和 在 上单调递减,
所以函数 在 上单调递减,与题意不相符;
若 , , ,
当 时,易知 在 上单调递减,有 ,
当 时, ,
则函数 在 上单调递 减,则 ,与题意不相符;
当 时, , ,
对于对勾函数 ,在 上和 单调递减,在 和 上单调递增,
则函数 在 上单调递增,在 上单调递减,
且对于 ,使得 ,
所以存在 , 使得 成立,
所以 .即实数 的取值范围为 .
因此正确答案为: .
四、解答题
17、
【答 案】
, , U U
【分析】
U ,
, U ,
, U ,
由 ,得
, ,
. U U
18、
【答案 】
(1)
(2)答案见详解
【分析】
(1)因为 解集为 或 ,所以 ,解得 ;
(2)若选① ,则 ,
令 得 ,
当 时, 的解集为 ;
当 时, 的解为 ;
当 时, 的解为 ;
若选② ,则 ,令 得
当 时, 的解集为 ;
当 时, 的解集为 ;
当 时, 的解集为 .
19、
【答案 】
(1)
(2)
【分析】
(1)因为 是幂函数,所以 ,解得 或 ,又函数为偶函
数,故 , ;
(2)原题可等价转化为 对 恒成立,
当 时恒成立;
当 时,分离参数得 ,即 ,由对勾函数图象特点可知 在
上单减,故 ,所以 ;
当 时,分离参数得 ,由对勾函数图象特点可知 在 上单减,
,所以 ,
所以
20、
【答案 】
(1) ;
(2)投资生态治理项目资金为5百万元,投资发展特色产业项目资金为95百万元时,总收益最大,且最大收益为
190.5百万元.
【分析】
(1)通过题意知,设 ,则 ,解得 ,所以 ,
所以 ,
即
(2)由(1),得
,
当且仅当 即 时,等号成立,
此时 ,
所以投资生态治理项 目资金为5百万元,投资发展特色产业项目资金为95百万元时,
总收益最大,且最大收益为190.5百万元.
21、
【答案 】
(1)
(2) 或
【分析】
(1)由 得 ,即 ,
因为奇函数的定义域关于原点对称,则必有 ,
此时 ,证明如下:
函数 是奇函数
(2)函数 在 上单调递增,
任取
则
,
又
,
即 ,
所以函数 在 上单调递增,
已知 , ,
所以 ,
又 ,
,
解得 或
22、
【答 案】
(1)
(2)
【分析】
(1)解:当 时, , ,
由 ,解得 ,
由 ,解得 或 ,
即 ,
,
,
当 时 ,函数在 上单调递增,在 上单调递减,
当 时 ,函数在 上单调递增,
故函数 的单调递减区间为 .
(2)解:令 ,
得 ,解得 或 ,
,解得 ,
,解得 或 ,
,
, ,
又因为函数 关于直线 对称,
故 ,
所以 ,
令 ,由 ,得 ,
由 ,有 成立,
可知 ,
故 ,
又 时, ,
所以 ,解得 .
同课章节目录
