2022~2023学年甘肃白银靖远县靖远县第一中学高三上学期期末文科数学试卷(图片版,含解析)
文档属性
| 名称 | 2022~2023学年甘肃白银靖远县靖远县第一中学高三上学期期末文科数学试卷(图片版,含解析) |

|
|
| 格式 | |||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-01 00:00:00 | ||
图片预览




文档简介
2022~2023学年甘肃白银靖远县靖远县第一中学高三上学期期末文科数学
试卷
一、单选题(本大题共12小题,每小题5分,共60分)
1、已知集合 Z ,则 的元素个数为( )
A.1
B.3
C.5
D.7
i
2、 ( )
i
A. i
B. i
C. i
D. i
3、下列坐标所表示的点是函数 图象的对称中心的是( )
A.
B.
C.
D.
4、抛物线 的准线方程为( )
A.
B.
C.
D.
5、若tan ,则tan ( )
A.
B.
C.
D.
6、函数 的零点为( )
A.4
B.4或5
C.5
D. 或5
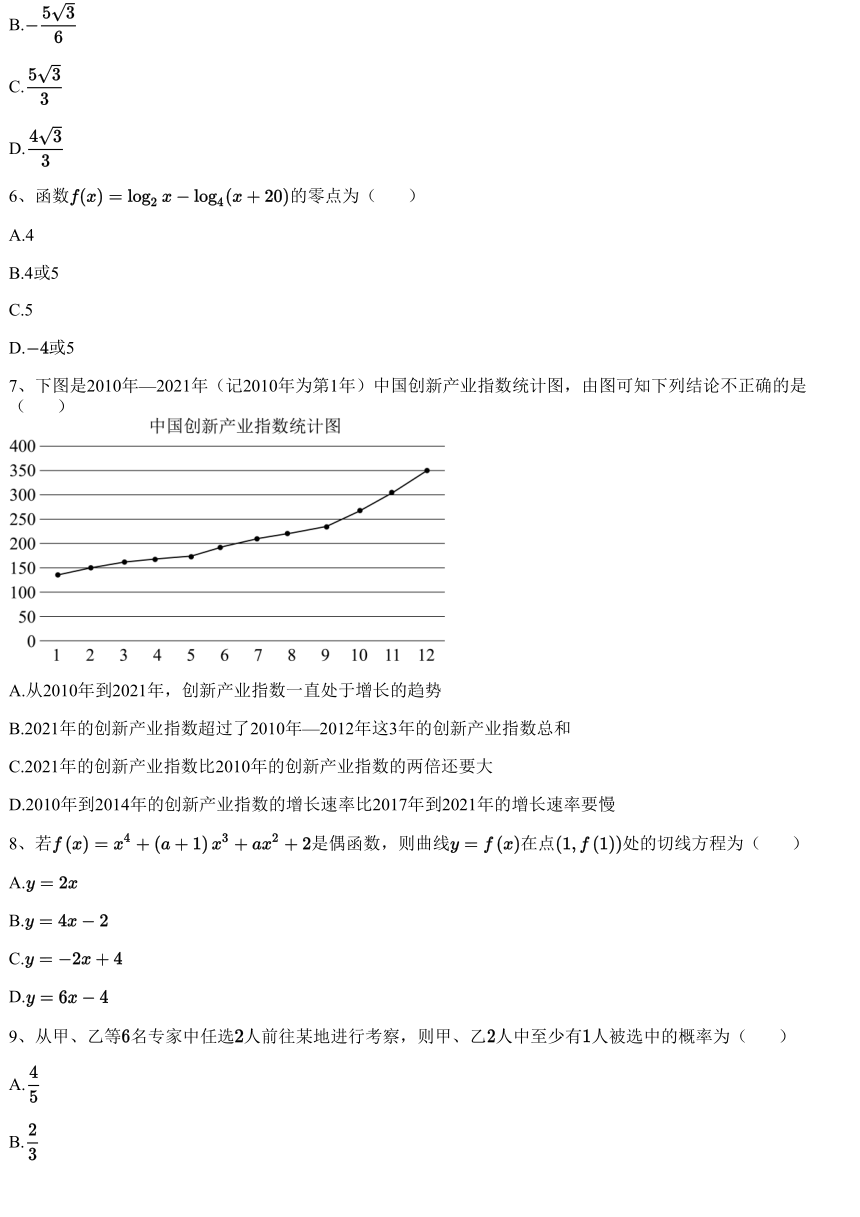
7、下图是2010年—2021年(记2010年为第1年)中国创新产业指数统计图,由图可知下列结论不正确的是
( )
A.从2010年到2021年,创新产业指数一直处于增长的趋势
B.2021年的创新产业指数超过了2010年—2012年这3年的创新产业指数总和
C.2021年的创新产业指数比2010年的创新产业指数的两倍还要大
D.2010年到2014年的创新产业指数的增长速率比2017年到2021年的增长速率要慢
8、若 是偶函数,则曲线 在点 处的切线方程为( )
A.
B.
C.
D.
9、从甲、乙等 名专家中任选 人前往某地进行考察,则甲、乙 人中至少有 人被选中的概率为( )
A.
B.
C.
D.
10、已知 的内角 , , 所对的边分别为 , , , , , ,则 的面
积为( ).
A.
B.
C.
D.
11、已知 ,则 ( )
A.
B.
C.
D.
12、已知 , 分别是双曲线 的左、右焦点,直线l经过 且与C左支交于P,
Q两点,P在以 为直径的圆上, ,则C的离心率是( )
A.
B.
C.
D.
二、填空题(本大题共4小题,每小题5分,共20分)
13、设 满足约束条件 ,则 的最大值为 .
14、已知向量 , ,若 ,则 .
15、若甲、乙两个圆柱形容器的容积相等,且甲、乙两个圆柱形的容器内部底面半径的比值为2,则甲、乙两个
圆柱形容器内部的高度的比值为 .
16、如图,在正三棱柱 中, , 为 的中点,则 与 所成角的余弦
值为 .
三、解答题(本大题共7小题,共70分)
17、(本小题8分)
年 月 日 时 分,长征四号丙运载火箭在酒泉卫星发射中心点火起飞,随后将遥感三十四号 星送入
预定轨道发射,大量观众通过某网络直播平台观看了发射全过程.为了解大家是否关注航空航天技术,该平台
随机抽取了 名用户进行调查,相关数据如下表.
关注 不关注 合计
男性用户
女性用户
合计
(1)补充表格数据并根据表中数据分别估计男、女性用户关注航空航天技术的概率;
(2)能否有 的把握认为是否关注航空航天技术与性别有关?
附: , .
18、(本小题8分)
在等比数列 中, ,且 .
(1)求 的通项公式;
(2)若 ,求数列 的前 项和 .
19、(本小题8分)
如图,在四棱锥 中,底面 是边长为 的菱形, 分别是 的中点, 平面
, ,且 .
(1)证明: 平面 .
(2)求四棱锥 的体 积.
20、(本小题10分)
已知椭圆C: 与椭圆 的离心率相同, 为椭圆C上一点.
(1)求椭圆C的方程.
(2)若过点 的直线l与椭圆C相交于A,B两点,试问以AB为直径的圆是否经过定点 ?若存在,求出 的
坐标;若不存在,请说明理由.
21、(本小题12分)
已知函数 e
(1)若 ,证明: 存在唯一极值点.
(2)若 ,证明: , ,
e
22、(本小题12分)
在直角坐标系 中,曲线 的参数方程为 ( 为参数),以坐标原点为极点,x轴的正半轴为极轴,
建立极坐标系,曲线 的极坐标方程为 sin .
4
(1)写出 的普通方程和 的直角坐标方程;
(2)若曲线 与曲线 交于 两点, 的直角 坐标为 ,求 .
23、(本小题12分)
已知函数 .
(1)求不等式 的解集;
(2)若 的最小值为 ,求 的最小值.
参考答案
一、单选题
1、
【答 案】
C
【分析】
通过题意 ,所以 ,
所以 ,共 个元素.
因此正确答案为:C
2、
【答 案】
C
【分析】
i i i i
i.
i i i
因此正确答案为:C.
3、
【答 案】
A
【分析】
因为正弦函数的对称中心为 ,所以令 ,
解得: ,当 时,对称中心为 ,
即A是对称中心,其它各项均不是对称中心.
因此正确答案为: .
4、
【答 案】
C
【分析】
因为 ,所以 ,
所以抛物线 的准线 方程为 .
因此正确答案为:C
5、
【答 案】
C
【分析】
tan ,
因此正确答案为:C
6、
【答 案】
C
【分析】
通过题意可得: ,解得 ,故 的定义域为 ∞ ,
令 ,得 ,则 ,解得 或
,
又∵ ,所以 .
因此正确答案为:C.
7、
【答 案】
B
【分析】
从统计图可看出从2010年到2021年,创新产业指数一直处于增长的趋势,A无误;
从统计图估计得到2021年的创新产业指数大约为350,
而2010年—2012年这3年的创新产业指数总和大约为 ,
故2021年的创新产业指数没有超过2010年—2012年这3年的创新产业指 数总和,B有误;
因为2021年的创新产业指数大约为350,2010年的创业指数小于150,
,故2021年的创新产业指数比2010年的创新产业指数的 两倍还要大,C无误;
2010年到2014年的创新产业指数的折线倾斜程度小,而2017年到2021年的创业指数的折线倾 斜程度大,
故2010年到2014年的创新产业指数的增长速率比2017年到2021年的增长速率要慢,D无误.
因此正确答案为:B
8、
【答 案】
A
【分析】
为偶函数, ,
即 , ,解得: ,
,则 , ,
, 在点 处的切线方程为 ,即 .
因此正确答案为:A.
9、
【答 案】
D
【分析】
记其他 名专家分别为 ,将甲、乙分别记为 ,
从 人中任选 人,则有 , , , , , , , , , ,
, , , , ,共 种情况;
其中甲、乙至少有 人被选中的有 , , , , , , , , ,共
种情况,
甲、乙至少有 人被选中的概率 .
因此正确答案为:D.
10、
【答 案】
C
【分析】
由余弦定理得: ,
即 ,
即 ,
即 ,
所以 (负值舍去),
又因为 , 为三角形内角,
所以 ,
所以 ,
所以 的面积为 .
故选:C.
11、
【答 案】
A
【分析】
解:因为 ,
所以 ,
所以 ,
又因为 ,
所以 ,
所以 .
因此正确答案为:A.
12、
【答案 】
A
【分析】
不妨设 , ,
因为P在以 为直径的圆上,所以 ,即 ,则 .
因为Q在C的左支上,所以 ,
即 ,解得 ,则 .
因为 ,所以 ,即 ,
故 ,
故 .
因此正确答案为:A
二、填空题
13、
【答案 】
【分析】
由约束条件可得可行域如下图阴影部分所示,
若 取得最大值,则 在 轴截距取得最小值,
由图像分析可得:当 过点 时,在 轴截距最小,
由 得: ,即 , .
因此正确答案为: .
14、
【答案 】
【分析】
因为 ,
所以 ,
所以 ,
所以 ,
所以 ,
所以 ,
解得 ,
因此正确答案为: .
15、
【答案 】
/
【分析】
设甲的底面半径为 ,则乙的底面半径为 ,
设甲的高为 ,乙的高为 ,
通过题意, ,
所以 .
因此正确答案为:
16、
【答案 】
【分析】
如下图所示,取 的中点 ,连接 , ,
在 中, 为 的中点,所以 为中位线,所以 // ,
所以 为 与 所成的角,
在 中, , , ,
所以 ,
所以 与 所成角的余弦值为 .
因此正确答案为:
三、解答题
17、
【答案 】
(1)表格见解析,男性关注的概率为 ;女性关注的概率为
(2)没有 的把握认为是否关注航空航天技术与性别有关
【分析】
(1)由已知数据可补充表格如下:
关注 不关注 合计
男性用户
女性用户
合计
估计男性用户关注航空航天技术的概率 ;女性用户关注航空航天技术的概率 .
(2) ,
没有 的把握认为是否关注航空航天技术与性别有关.
18、
【答案 】
(1)
(2)
【分析】
(1)由 得: ,
又 , ,
设等比数列 的公比为 ,则 ,
所以 ;
(2)由(1)得: ,
.
19、
【答 案】
(1)证明见解析
(2)
【分析】
(1) 分别是 的中点,四边形 为菱形, , ,
四边形 为平行四边形, ,
又 \n 平面 , 平面 , 平面 ;
分别为 的中点, ,
又 \n 平面 , 平面 , 平面 ,
又 , 平面 , 平面 平面 ,
平面 , 平面 .
(2)连接 ,
平面 , 平面 , ,又 , .
为 的中点, ,又 , 为等边三角形,
, ;
延长 至点 ,使得 ,
由(1)知: 平面 ,又 平面 , ,
又 , 平面 , 平面 ,
, , ,
,
.
20、
【答 案】
(1)
(2)存在 的坐标为 ,理由见解析
【分析】
(1)在椭圆 中, , , ,离心率 ,
在椭圆C: 中, ,
所以 ,化简得 ,
因为 在椭圆C: 上,
所以 ,所以 ,所以 , ,
所以椭圆 .
(2)当直线 的斜率为0时,线段 是椭圆的短轴,以AB为直径的圆的方程为 ,
当直线 的斜率不存在时,直线 的方程为 ,代入 ,得 ,以AB为直径的圆的方程为
,
联立 ,解得 ,
由此猜想存在 ,使得以AB为直径的圆是经过定点 ,
证明如下:
当直线 的斜率不为0且斜率存在时,设直线 ,
联立 ,消去 并整理得 ,
,
设 、 ,
则 , ,
则 ,
,
因为
,
所以 ,所以点 在以 为直径的圆上,
综上所述:以AB为直径的圆是经过定点 .
21、
【答 案】
(1)见解析;
(2)见解析;
【分析】
(1)证明:因为 e ,
所以 e ,
易知 在 上单调递减,
又因为 e< 0, e>0,
所以存在唯一个 ,使得 ,
当 时, , 单调递增;
当 时, , 单调递减 ;
所以 存在唯一极值点;
2 ( )证明:要证明 在 , 上恒成立,
即要证明 e 在 , 上恒成立,
e
也即证明 在 , 上恒成立,
e
令 ,
即证明 在 , 上恒成立,
, 又因为 在 上单调递增,
所以 ,
e
所以原命题等价于证明 在 , 上恒成立,
e
又因为 e ,
令 ,
则 ,
因为 ,
e
所以 e, ,
当 时, ,
e
所以当 时, , 单调递减;
当 时, , 单调递增;
所以 ;
e
当 时, e , e 在 , 上恒成立,
e , 所以 在 上单调递增,
所以 ;
当 时, , 在 , 上恒成立,
, 所以 在 上单调递增,
所以 ;
e
综上所述: 在 , 上恒成立,
所以原命题得证.
22、
【答案 】
(1) : , :.
(2)
【分析】
(1)由 消去 得 ,即 ,
由 sin 得 sin ,即
4
(2)直线 经过点 ,且倾斜角为 ,所以 的方程写成标准参数方程为 ( 为参
数),将其代入 : 得 ,
设 所对应的参数分别为 ,则 , 故 ,
因此 ,
23、
【答案 】
(1)
(2)3
【分析】
(1)通过题意分析可以得: ,
所以 ,
,
.
综上: ,
所以 的解集为 .
(2) ,所以 .
所以 .
所以 ,
当且仅当 ,即 等号成立.
所以 的最小值为 .
试卷
一、单选题(本大题共12小题,每小题5分,共60分)
1、已知集合 Z ,则 的元素个数为( )
A.1
B.3
C.5
D.7
i
2、 ( )
i
A. i
B. i
C. i
D. i
3、下列坐标所表示的点是函数 图象的对称中心的是( )
A.
B.
C.
D.
4、抛物线 的准线方程为( )
A.
B.
C.
D.
5、若tan ,则tan ( )
A.
B.
C.
D.
6、函数 的零点为( )
A.4
B.4或5
C.5
D. 或5
7、下图是2010年—2021年(记2010年为第1年)中国创新产业指数统计图,由图可知下列结论不正确的是
( )
A.从2010年到2021年,创新产业指数一直处于增长的趋势
B.2021年的创新产业指数超过了2010年—2012年这3年的创新产业指数总和
C.2021年的创新产业指数比2010年的创新产业指数的两倍还要大
D.2010年到2014年的创新产业指数的增长速率比2017年到2021年的增长速率要慢
8、若 是偶函数,则曲线 在点 处的切线方程为( )
A.
B.
C.
D.
9、从甲、乙等 名专家中任选 人前往某地进行考察,则甲、乙 人中至少有 人被选中的概率为( )
A.
B.
C.
D.
10、已知 的内角 , , 所对的边分别为 , , , , , ,则 的面
积为( ).
A.
B.
C.
D.
11、已知 ,则 ( )
A.
B.
C.
D.
12、已知 , 分别是双曲线 的左、右焦点,直线l经过 且与C左支交于P,
Q两点,P在以 为直径的圆上, ,则C的离心率是( )
A.
B.
C.
D.
二、填空题(本大题共4小题,每小题5分,共20分)
13、设 满足约束条件 ,则 的最大值为 .
14、已知向量 , ,若 ,则 .
15、若甲、乙两个圆柱形容器的容积相等,且甲、乙两个圆柱形的容器内部底面半径的比值为2,则甲、乙两个
圆柱形容器内部的高度的比值为 .
16、如图,在正三棱柱 中, , 为 的中点,则 与 所成角的余弦
值为 .
三、解答题(本大题共7小题,共70分)
17、(本小题8分)
年 月 日 时 分,长征四号丙运载火箭在酒泉卫星发射中心点火起飞,随后将遥感三十四号 星送入
预定轨道发射,大量观众通过某网络直播平台观看了发射全过程.为了解大家是否关注航空航天技术,该平台
随机抽取了 名用户进行调查,相关数据如下表.
关注 不关注 合计
男性用户
女性用户
合计
(1)补充表格数据并根据表中数据分别估计男、女性用户关注航空航天技术的概率;
(2)能否有 的把握认为是否关注航空航天技术与性别有关?
附: , .
18、(本小题8分)
在等比数列 中, ,且 .
(1)求 的通项公式;
(2)若 ,求数列 的前 项和 .
19、(本小题8分)
如图,在四棱锥 中,底面 是边长为 的菱形, 分别是 的中点, 平面
, ,且 .
(1)证明: 平面 .
(2)求四棱锥 的体 积.
20、(本小题10分)
已知椭圆C: 与椭圆 的离心率相同, 为椭圆C上一点.
(1)求椭圆C的方程.
(2)若过点 的直线l与椭圆C相交于A,B两点,试问以AB为直径的圆是否经过定点 ?若存在,求出 的
坐标;若不存在,请说明理由.
21、(本小题12分)
已知函数 e
(1)若 ,证明: 存在唯一极值点.
(2)若 ,证明: , ,
e
22、(本小题12分)
在直角坐标系 中,曲线 的参数方程为 ( 为参数),以坐标原点为极点,x轴的正半轴为极轴,
建立极坐标系,曲线 的极坐标方程为 sin .
4
(1)写出 的普通方程和 的直角坐标方程;
(2)若曲线 与曲线 交于 两点, 的直角 坐标为 ,求 .
23、(本小题12分)
已知函数 .
(1)求不等式 的解集;
(2)若 的最小值为 ,求 的最小值.
参考答案
一、单选题
1、
【答 案】
C
【分析】
通过题意 ,所以 ,
所以 ,共 个元素.
因此正确答案为:C
2、
【答 案】
C
【分析】
i i i i
i.
i i i
因此正确答案为:C.
3、
【答 案】
A
【分析】
因为正弦函数的对称中心为 ,所以令 ,
解得: ,当 时,对称中心为 ,
即A是对称中心,其它各项均不是对称中心.
因此正确答案为: .
4、
【答 案】
C
【分析】
因为 ,所以 ,
所以抛物线 的准线 方程为 .
因此正确答案为:C
5、
【答 案】
C
【分析】
tan ,
因此正确答案为:C
6、
【答 案】
C
【分析】
通过题意可得: ,解得 ,故 的定义域为 ∞ ,
令 ,得 ,则 ,解得 或
,
又∵ ,所以 .
因此正确答案为:C.
7、
【答 案】
B
【分析】
从统计图可看出从2010年到2021年,创新产业指数一直处于增长的趋势,A无误;
从统计图估计得到2021年的创新产业指数大约为350,
而2010年—2012年这3年的创新产业指数总和大约为 ,
故2021年的创新产业指数没有超过2010年—2012年这3年的创新产业指 数总和,B有误;
因为2021年的创新产业指数大约为350,2010年的创业指数小于150,
,故2021年的创新产业指数比2010年的创新产业指数的 两倍还要大,C无误;
2010年到2014年的创新产业指数的折线倾斜程度小,而2017年到2021年的创业指数的折线倾 斜程度大,
故2010年到2014年的创新产业指数的增长速率比2017年到2021年的增长速率要慢,D无误.
因此正确答案为:B
8、
【答 案】
A
【分析】
为偶函数, ,
即 , ,解得: ,
,则 , ,
, 在点 处的切线方程为 ,即 .
因此正确答案为:A.
9、
【答 案】
D
【分析】
记其他 名专家分别为 ,将甲、乙分别记为 ,
从 人中任选 人,则有 , , , , , , , , , ,
, , , , ,共 种情况;
其中甲、乙至少有 人被选中的有 , , , , , , , , ,共
种情况,
甲、乙至少有 人被选中的概率 .
因此正确答案为:D.
10、
【答 案】
C
【分析】
由余弦定理得: ,
即 ,
即 ,
即 ,
所以 (负值舍去),
又因为 , 为三角形内角,
所以 ,
所以 ,
所以 的面积为 .
故选:C.
11、
【答 案】
A
【分析】
解:因为 ,
所以 ,
所以 ,
又因为 ,
所以 ,
所以 .
因此正确答案为:A.
12、
【答案 】
A
【分析】
不妨设 , ,
因为P在以 为直径的圆上,所以 ,即 ,则 .
因为Q在C的左支上,所以 ,
即 ,解得 ,则 .
因为 ,所以 ,即 ,
故 ,
故 .
因此正确答案为:A
二、填空题
13、
【答案 】
【分析】
由约束条件可得可行域如下图阴影部分所示,
若 取得最大值,则 在 轴截距取得最小值,
由图像分析可得:当 过点 时,在 轴截距最小,
由 得: ,即 , .
因此正确答案为: .
14、
【答案 】
【分析】
因为 ,
所以 ,
所以 ,
所以 ,
所以 ,
所以 ,
解得 ,
因此正确答案为: .
15、
【答案 】
/
【分析】
设甲的底面半径为 ,则乙的底面半径为 ,
设甲的高为 ,乙的高为 ,
通过题意, ,
所以 .
因此正确答案为:
16、
【答案 】
【分析】
如下图所示,取 的中点 ,连接 , ,
在 中, 为 的中点,所以 为中位线,所以 // ,
所以 为 与 所成的角,
在 中, , , ,
所以 ,
所以 与 所成角的余弦值为 .
因此正确答案为:
三、解答题
17、
【答案 】
(1)表格见解析,男性关注的概率为 ;女性关注的概率为
(2)没有 的把握认为是否关注航空航天技术与性别有关
【分析】
(1)由已知数据可补充表格如下:
关注 不关注 合计
男性用户
女性用户
合计
估计男性用户关注航空航天技术的概率 ;女性用户关注航空航天技术的概率 .
(2) ,
没有 的把握认为是否关注航空航天技术与性别有关.
18、
【答案 】
(1)
(2)
【分析】
(1)由 得: ,
又 , ,
设等比数列 的公比为 ,则 ,
所以 ;
(2)由(1)得: ,
.
19、
【答 案】
(1)证明见解析
(2)
【分析】
(1) 分别是 的中点,四边形 为菱形, , ,
四边形 为平行四边形, ,
又 \n 平面 , 平面 , 平面 ;
分别为 的中点, ,
又 \n 平面 , 平面 , 平面 ,
又 , 平面 , 平面 平面 ,
平面 , 平面 .
(2)连接 ,
平面 , 平面 , ,又 , .
为 的中点, ,又 , 为等边三角形,
, ;
延长 至点 ,使得 ,
由(1)知: 平面 ,又 平面 , ,
又 , 平面 , 平面 ,
, , ,
,
.
20、
【答 案】
(1)
(2)存在 的坐标为 ,理由见解析
【分析】
(1)在椭圆 中, , , ,离心率 ,
在椭圆C: 中, ,
所以 ,化简得 ,
因为 在椭圆C: 上,
所以 ,所以 ,所以 , ,
所以椭圆 .
(2)当直线 的斜率为0时,线段 是椭圆的短轴,以AB为直径的圆的方程为 ,
当直线 的斜率不存在时,直线 的方程为 ,代入 ,得 ,以AB为直径的圆的方程为
,
联立 ,解得 ,
由此猜想存在 ,使得以AB为直径的圆是经过定点 ,
证明如下:
当直线 的斜率不为0且斜率存在时,设直线 ,
联立 ,消去 并整理得 ,
,
设 、 ,
则 , ,
则 ,
,
因为
,
所以 ,所以点 在以 为直径的圆上,
综上所述:以AB为直径的圆是经过定点 .
21、
【答 案】
(1)见解析;
(2)见解析;
【分析】
(1)证明:因为 e ,
所以 e ,
易知 在 上单调递减,
又因为 e< 0, e>0,
所以存在唯一个 ,使得 ,
当 时, , 单调递增;
当 时, , 单调递减 ;
所以 存在唯一极值点;
2 ( )证明:要证明 在 , 上恒成立,
即要证明 e 在 , 上恒成立,
e
也即证明 在 , 上恒成立,
e
令 ,
即证明 在 , 上恒成立,
, 又因为 在 上单调递增,
所以 ,
e
所以原命题等价于证明 在 , 上恒成立,
e
又因为 e ,
令 ,
则 ,
因为 ,
e
所以 e, ,
当 时, ,
e
所以当 时, , 单调递减;
当 时, , 单调递增;
所以 ;
e
当 时, e , e 在 , 上恒成立,
e , 所以 在 上单调递增,
所以 ;
当 时, , 在 , 上恒成立,
, 所以 在 上单调递增,
所以 ;
e
综上所述: 在 , 上恒成立,
所以原命题得证.
22、
【答案 】
(1) : , :.
(2)
【分析】
(1)由 消去 得 ,即 ,
由 sin 得 sin ,即
4
(2)直线 经过点 ,且倾斜角为 ,所以 的方程写成标准参数方程为 ( 为参
数),将其代入 : 得 ,
设 所对应的参数分别为 ,则 , 故 ,
因此 ,
23、
【答案 】
(1)
(2)3
【分析】
(1)通过题意分析可以得: ,
所以 ,
,
.
综上: ,
所以 的解集为 .
(2) ,所以 .
所以 .
所以 ,
当且仅当 ,即 等号成立.
所以 的最小值为 .
同课章节目录
