2022~2023学年广东深圳罗湖区深圳中学高二下学期期中数学试卷(图片版,含解析)
文档属性
| 名称 | 2022~2023学年广东深圳罗湖区深圳中学高二下学期期中数学试卷(图片版,含解析) |
|
|
| 格式 | |||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-01 17:26:50 | ||
图片预览




文档简介
2022~2023学年广东深圳罗湖区深圳中学高二下学期期中数学试卷
一、选择题(本大题共8小题,每小题5分,共40分)
1、已知函数 ,则 ( ).
A.
B.
C.
D.
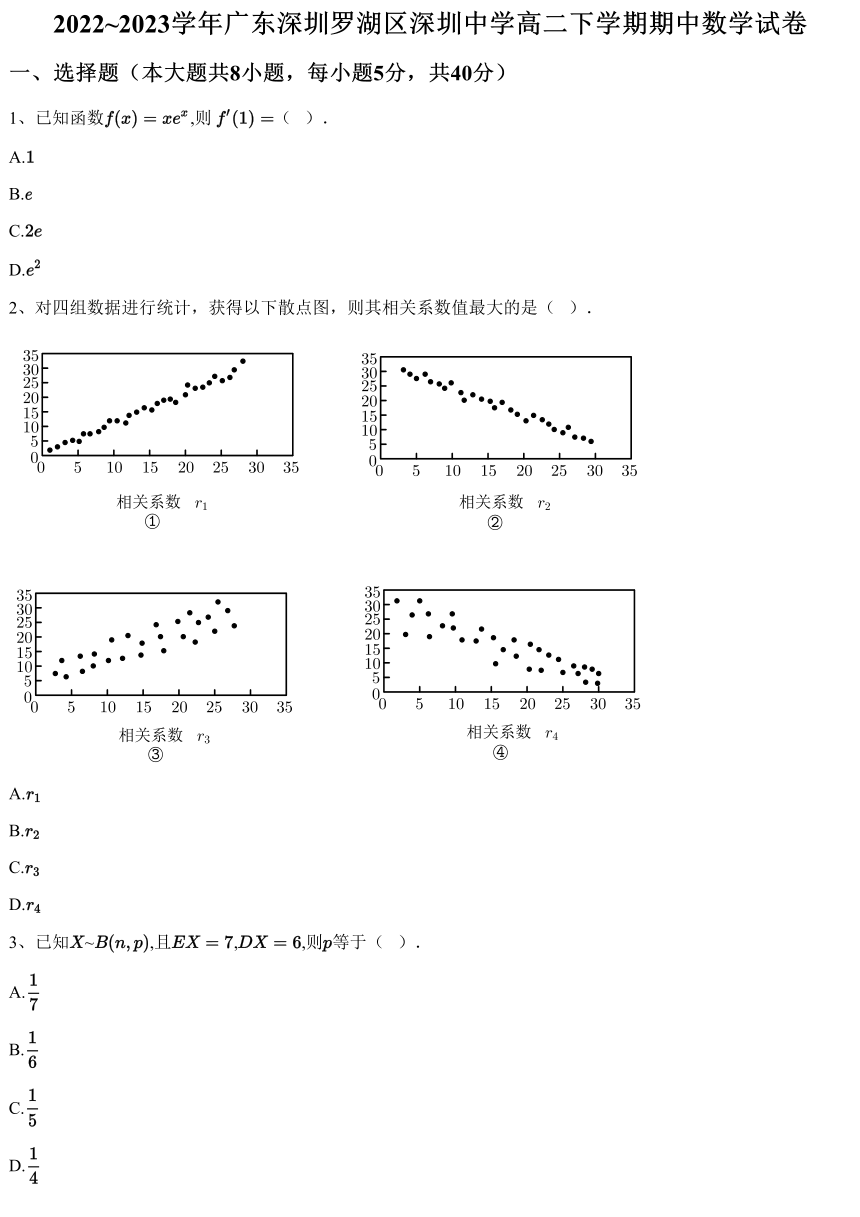
2、对四组数据进行统计,获得以下散点图,则其相关系数值最大的是( ).
相关系数 相关系数
相关系数 相关系数
A.
B.
C.
D.
3、已知 ~ ,且 , ,则 等于( ).
A.
B.
C.
D.
4、一袋中装有10个球,其中3个黑球、7个白球,从中先后随意各取一球(不放回),则第二次取到的是黑球的概
率为( )
A.
B.
C.
D.
5、已知从某批材料中任取一件时,取得的这件材料的强度 ~ ,则取得的这件材料的强度介于 到
之间的概率为( ).
附:若 , 则 , ,
A.
B.
C.
D.
6、某一离散型随机变量的分布列为
且 ,则 的值为( ).
A.
B.
C.
D.
7、已知函数 ,则 的图象大致为( ).
y
x
A. O
y
x
O
B.
y
x
O
C.
y
E x
O
D.
8、当 时,下列不等式正确的是( ).
A.
B.
C.
D.
二、多项选择题(本大题共4小题,每小题5分,共20分)
9、关于 的展开式,下列结论正确的是( ).
A.奇数项的二项式系数和为
B.所有项的系数和为
C.只有第 项的二项式系数最大
D.含 项的系数为
10、关于随机事件 下列说法正确的是( ).
A.若 ,则 独立
B.若 ,则
C.若 ,则
D.若事件 和 是两个互斥事件,则
11、设函数 的定义域为 , 是 的极大值点,以下结论一定正确的是( ).
A. ,
B. 是 的极大值点
C. 是 的极小值点
D. 是 的极小值点
12、已知函数 , ),其中 ,则( ).
A.存在过点 与函数 、 图象均相切的直线
B.当 , 时,不存在与函数 、 图象均相切的直线
C.当 , 时,存在两条与函数 、 图象均相切的直线
D.最多存在三条与函数 、 图象均相切的直线
三、填空题(本大题共4小题,每小题5分,共20分)
13、画出一个 列联表:
总计
总计
则表中 , 处的值分别为 ; .
14、甲、乙两人进行羽毛球比赛,比赛采取五局三胜制,无论哪一方先胜三局比赛都结束,假定甲每局比赛获
胜的概率均为 ,则甲以 的比分获胜的概率为 .
15、随机变量 的取值为 .若 , ,则 .
16、已知函数 ,若 存在唯一的零点 ,且 ,则 的取值范围为 .
四、解答题(本大题共6小题,共70分)
17、(本小题10分)
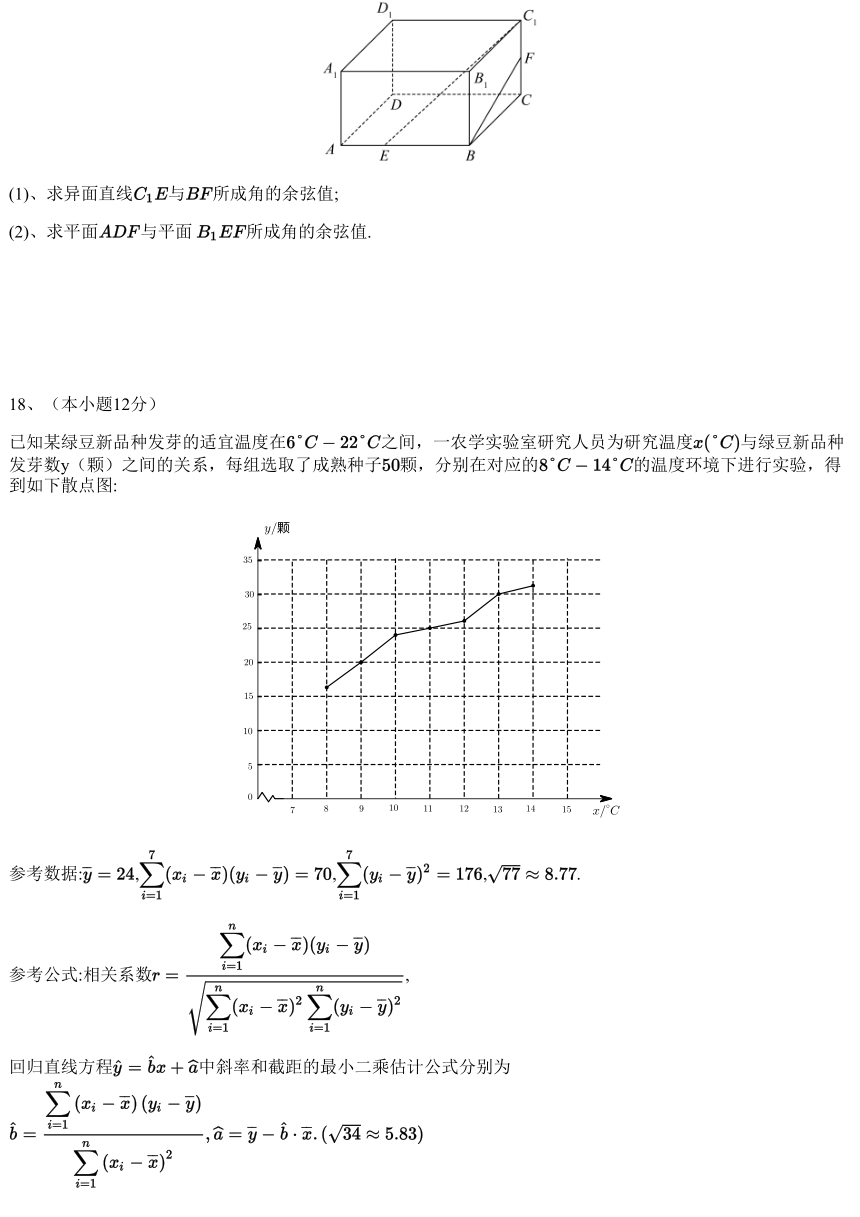
如图,已知长方体 , , , , , .
(1)、求异面直线 与 所成角的余弦值;
(2)、求平面 与平面 所成角的余弦值.
18、(本小题12分)
已知某绿豆新品种发芽的适宜温度在 之间,一农学实验室研究人员为研究温度 与绿豆新品种
发芽数y(颗)之间的关系,每组选取了成熟种子 颗,分别在对应的 的温度环境下进行实验,得
到如下散点图:
颗
参考数据: , , , .
参考公式:相关系数 ,
回归直线方程 中斜率和截距的最小二乘估计公式分别为
(1)、由折线统计图看出,可用线性回归模型拟合 与 的关系,请用相关系数加以说明;
(2)、建立 关于 的回归方程,并预测在 C的温度下,种子发芽的颗数.
19、(本小题12分)
若函数 .
(1)、当 时,求函数 的单调区间;
(2)、在 处有极值为-2,求 的值.
20、(本小题12分)
深圳中学足球社团是一个受学生欢迎的社团.
(1)、现社团招新,需对报名者进行“点球测试”来决定是否录取,规则如下:踢点球一次,若踢进,则被录取,
若没踢进,则继续踢,直到踢进为止,但是每人最多踢点球 次, 某同学进行“点球测试”,依据平时的训练数
据,获得其单次点球踢进的概率为 ,该同学每次点球是否踢进相互独立.他在测试中所踢的点球次数记为
,求 的分布列及数学期望.
(2)、社团中的甲、乙、丙三名成员将进行传球训练,从甲开始随机地将球传给其他两人中的任意一人,接球者
再随机地将球传给其他两人中的任意一人,如此不停地传下去,且假定每次传球都能被接到.记开始传球的人
为第 次触球者,第 次触球者是甲的概率记为 ,即 .
(i) 证明:数列 为等比数列.
(ii)判断第 次还是第 次触球者是甲的概率大.
21、(本小题12分)
函数 .
(1)、若函数 存在过 的切线,求实数 的取值范围;
(2)、若 , 函数 在区间 上最大值为 ,最小值为 ,求 的最小值.
22、(本小题12分)
已知函数 , .
(1)、若 ,求 的取值范围;
(2)、当 时,证明:
参考答案
一、选择题
1、
【答 案】
C
【分析】
,则
2、
【答 案】
A
【分析】
由图中显然①与③为正相关,②与④为负相关,故 , , , ;并从图中可看出 , 更接近 ,
可得答案A
3、
【答 案】
A
【分析】
已知 ~ , , ,则
4、
【答 案】
B
【分析】
设事件 :表示第1次取到黑球,事件 :表示第1次取到白球,
事件 :表示第2次取到黑球,可得 ,
则 .
因此正确答案为:B.
5、
【答 案】
D
【分析】
因为 ~ , , ,
所以
6、
【答 案】
B
【分析】
依题意得
,
解得 ,
∴ .
7、
【答 案】
B
【分析】
设 ,
则 ,
∴ 在 上为增函数,在 上为减函数,
∴ ,
∴ ,
得当 或 时,均有 ,排除ACD.
故选B.
8、
【答 案】
C
【分析】
令 , ,
当 时, , ,
则 , 在 上单调递减,
又 ,
则
又
则
二、多项选择题
9、
【答 案】
B;D
【分析】
略
10、
【答案 】
A;B;D
【分析】
略
11、
【答 案】
B;C;D
【分析】
极大值不一定是最大值,因此不满足在整个定义域上值最大,故A错误.
是把 的图像关于 轴对称,
因此 是 的极大值点,故B正确.
是把 的图像关于 轴对称,
因此 是 的极小值点,故C正确.
是把 的图像关于原点做对称,
因此 是 的极小值点,故D正确.
12、
【答案 】
B;C
【分析】
已知 ,函数定义域为 ,
可得 ,
对于选项 ,易知函数 的图象恒过定点
所以切线斜率 ,切线方程为 ,
显然 不是函数 的切线,故选项A错误;
对于选项 ,当 , 时, , ,
假设存在公切线与 切点 ,
所以函数 在点 处的切线方程为 ,
即 ,
函数 在点 处的切线方程为 ,
即
其满足
所以
此时 ,
整理得 ,
即 ,①
不妨设 ,函数定义域为
可得 ,
当 时, 单调递减;
当 时, 单调递增,
所以 在 上取得极小值也是最小值,
所以 ,
其不满足①式,故 不存在,
所以不存在与函数 、 图象均相切的直线,
故选项B正确;
对于选项 ,当 , 时 , ,
可得
假设存在公切线与 切点 ,
所以函数 在点 处的切线方程为 ,
即
函数 在点 处的切线方程为
即
其满
所以
即 ②
不妨设 函数定义域为 ,
可得
当 时, 单调递增;
当 时, 单调递减,
所以 在 上取得极大值也是最大值,
此时方程②有两解,
所以存在 条公切线,故选项C正确;
对于选项 ,函数 、 至多存在两条公切线,故选项D错误.
故选:BC.
三、填空题
13、
【答案 】
;
【分析】
由题意可知:
,解得 .
故答案为: , .
14、
【答 案】
【分析】
甲以 的比分获胜,甲只能在第 、 、 次中失败 次,第 次获胜,因此所求概率为
15、
【答案 】
【分析】
设 ,
则 ,
从而由 ,
得 ,
故 .
故
16、
【答 案】
【分析】
令 ,即 ,显然 不是方程的根,
则 ,
令 ,
,
, 随 的变化如下表所示:
极小值 极大值
又 , ,
且 时, ,
且 时, ,
当 时, ,
时, ,
做出函数草图如下图所示:
故 ,
即 的取值范围为 .
四、解答题
17、
【答 案】
(1)、
(2)、
【分析】
(1)、以 为坐标原点,分别以 为 , , 轴的正方向,建立空间直角坐标系,则
故 ,
设异面直线 与 所成角为 ,
(2)、设 是平面 的法向量, ,
取 ,有
设 ) 是平面 的法向量,
,
则
取 ,有
设平面 与平面 所成角为 ,
18、
【答 案】
(1)、
暂无
(2)、
暂无
【分析】
(1)、由题意可知:
又
所以相关系数
因为相关系数 ,所以 与 的线性相关性较高,可以利用线性回归模型拟合 与 的关系.
(2)、由( )知
所以
所以
所以 与 的回归直线为
当 时,
即在 的温度下,种子发芽的颗数为 .
19、
【答 案】
(1)、
见解析
(2)、
【分析】
(1)、当 时,
若 , 恒成立,函数 的单调递增区间为
若 , 或 , ,函数 单调递增,
时, ,函数 单调递减
若 , 或 时, ,函数 单调递增,
时, ,函数 单调递减
综上: 时,函数 的单调递增区间为
, 时,函数 的单调递增区间为 ,
函数 的单调递减区间为
时,函数 的单调递增区间为 ,
函数 的单调递减区间为
(2)、 ,即 ,
消元有 ,
解得 或 .
当 时, , ,满足题意
当 时, , ,与存在极值点矛盾
故 , , .
20、
【答案 】
(1)、
见解析
(2)、
见解析
【分析】
(1)、因为该同学踢一次点球命中的概率 ,
由题意, 可能取 , , ,则 , ,
,
的分布列为
即 .
(2)、(i) 第 次触球者是甲的概率记为 ,
则当 时,第 次触球者是甲的概率为 ,第 次触球者不是甲的概率为 ,
则 ,
从而 ,
又 ,
是以 为首项,公比为 的等比数列.
(ii) ,
, ,
,
故第 次触球者是甲的概率大.
21、
【答 案】
(1)、
(2)、
【分析】
(1)、设切点为 ,则切线方程为
切线过点 ,故 ,整理得
令 最大值 ,故
(2)、(i)当 时, 恒成立,函数 在区间 上单调递减,
所以 ,所以 ,
令 ,则函数 在区间 上单调递增,
所以 的最小值为 ,即 的最小值为 .
(ⅱ)当 时,由 ,得 ,由 ,得
所以函数 在区间 上单调递减,在区间 上单调递增
所以
①当 时, ,此时
所以 ,
令 ,则
所以函数 在区间[ 上单调递增,
所以函数 的最小值为
所以 的最小值为
②当 时, ,
所以
所以
令 ,则 ,
所以函数 在区间( 上单调递减,
所
综止所述: 的最小值为
22、
【答案 】
(1)、
(2)、
见解析
【分析】
(1)、记 .
则 恒成立,即 .
∵ ,
当 ,当 ;
∴ 在 上单调递增,在 上单调递减
∴ ,解得 ·
∴实数 的取值范围是
(2)、记
在 上单调递增
令 ,
则 .所以 即 在 上单调递增
由 ,知
∴ 即
∴当 单调递减;当 单调递增.
∴
由(*)式,可得
代入(**)式,得
由(1)知,当 时有 ,故
由 ,
故 ,即 ,原不等式得证
一、选择题(本大题共8小题,每小题5分,共40分)
1、已知函数 ,则 ( ).
A.
B.
C.
D.
2、对四组数据进行统计,获得以下散点图,则其相关系数值最大的是( ).
相关系数 相关系数
相关系数 相关系数
A.
B.
C.
D.
3、已知 ~ ,且 , ,则 等于( ).
A.
B.
C.
D.
4、一袋中装有10个球,其中3个黑球、7个白球,从中先后随意各取一球(不放回),则第二次取到的是黑球的概
率为( )
A.
B.
C.
D.
5、已知从某批材料中任取一件时,取得的这件材料的强度 ~ ,则取得的这件材料的强度介于 到
之间的概率为( ).
附:若 , 则 , ,
A.
B.
C.
D.
6、某一离散型随机变量的分布列为
且 ,则 的值为( ).
A.
B.
C.
D.
7、已知函数 ,则 的图象大致为( ).
y
x
A. O
y
x
O
B.
y
x
O
C.
y
E x
O
D.
8、当 时,下列不等式正确的是( ).
A.
B.
C.
D.
二、多项选择题(本大题共4小题,每小题5分,共20分)
9、关于 的展开式,下列结论正确的是( ).
A.奇数项的二项式系数和为
B.所有项的系数和为
C.只有第 项的二项式系数最大
D.含 项的系数为
10、关于随机事件 下列说法正确的是( ).
A.若 ,则 独立
B.若 ,则
C.若 ,则
D.若事件 和 是两个互斥事件,则
11、设函数 的定义域为 , 是 的极大值点,以下结论一定正确的是( ).
A. ,
B. 是 的极大值点
C. 是 的极小值点
D. 是 的极小值点
12、已知函数 , ),其中 ,则( ).
A.存在过点 与函数 、 图象均相切的直线
B.当 , 时,不存在与函数 、 图象均相切的直线
C.当 , 时,存在两条与函数 、 图象均相切的直线
D.最多存在三条与函数 、 图象均相切的直线
三、填空题(本大题共4小题,每小题5分,共20分)
13、画出一个 列联表:
总计
总计
则表中 , 处的值分别为 ; .
14、甲、乙两人进行羽毛球比赛,比赛采取五局三胜制,无论哪一方先胜三局比赛都结束,假定甲每局比赛获
胜的概率均为 ,则甲以 的比分获胜的概率为 .
15、随机变量 的取值为 .若 , ,则 .
16、已知函数 ,若 存在唯一的零点 ,且 ,则 的取值范围为 .
四、解答题(本大题共6小题,共70分)
17、(本小题10分)
如图,已知长方体 , , , , , .
(1)、求异面直线 与 所成角的余弦值;
(2)、求平面 与平面 所成角的余弦值.
18、(本小题12分)
已知某绿豆新品种发芽的适宜温度在 之间,一农学实验室研究人员为研究温度 与绿豆新品种
发芽数y(颗)之间的关系,每组选取了成熟种子 颗,分别在对应的 的温度环境下进行实验,得
到如下散点图:
颗
参考数据: , , , .
参考公式:相关系数 ,
回归直线方程 中斜率和截距的最小二乘估计公式分别为
(1)、由折线统计图看出,可用线性回归模型拟合 与 的关系,请用相关系数加以说明;
(2)、建立 关于 的回归方程,并预测在 C的温度下,种子发芽的颗数.
19、(本小题12分)
若函数 .
(1)、当 时,求函数 的单调区间;
(2)、在 处有极值为-2,求 的值.
20、(本小题12分)
深圳中学足球社团是一个受学生欢迎的社团.
(1)、现社团招新,需对报名者进行“点球测试”来决定是否录取,规则如下:踢点球一次,若踢进,则被录取,
若没踢进,则继续踢,直到踢进为止,但是每人最多踢点球 次, 某同学进行“点球测试”,依据平时的训练数
据,获得其单次点球踢进的概率为 ,该同学每次点球是否踢进相互独立.他在测试中所踢的点球次数记为
,求 的分布列及数学期望.
(2)、社团中的甲、乙、丙三名成员将进行传球训练,从甲开始随机地将球传给其他两人中的任意一人,接球者
再随机地将球传给其他两人中的任意一人,如此不停地传下去,且假定每次传球都能被接到.记开始传球的人
为第 次触球者,第 次触球者是甲的概率记为 ,即 .
(i) 证明:数列 为等比数列.
(ii)判断第 次还是第 次触球者是甲的概率大.
21、(本小题12分)
函数 .
(1)、若函数 存在过 的切线,求实数 的取值范围;
(2)、若 , 函数 在区间 上最大值为 ,最小值为 ,求 的最小值.
22、(本小题12分)
已知函数 , .
(1)、若 ,求 的取值范围;
(2)、当 时,证明:
参考答案
一、选择题
1、
【答 案】
C
【分析】
,则
2、
【答 案】
A
【分析】
由图中显然①与③为正相关,②与④为负相关,故 , , , ;并从图中可看出 , 更接近 ,
可得答案A
3、
【答 案】
A
【分析】
已知 ~ , , ,则
4、
【答 案】
B
【分析】
设事件 :表示第1次取到黑球,事件 :表示第1次取到白球,
事件 :表示第2次取到黑球,可得 ,
则 .
因此正确答案为:B.
5、
【答 案】
D
【分析】
因为 ~ , , ,
所以
6、
【答 案】
B
【分析】
依题意得
,
解得 ,
∴ .
7、
【答 案】
B
【分析】
设 ,
则 ,
∴ 在 上为增函数,在 上为减函数,
∴ ,
∴ ,
得当 或 时,均有 ,排除ACD.
故选B.
8、
【答 案】
C
【分析】
令 , ,
当 时, , ,
则 , 在 上单调递减,
又 ,
则
又
则
二、多项选择题
9、
【答 案】
B;D
【分析】
略
10、
【答案 】
A;B;D
【分析】
略
11、
【答 案】
B;C;D
【分析】
极大值不一定是最大值,因此不满足在整个定义域上值最大,故A错误.
是把 的图像关于 轴对称,
因此 是 的极大值点,故B正确.
是把 的图像关于 轴对称,
因此 是 的极小值点,故C正确.
是把 的图像关于原点做对称,
因此 是 的极小值点,故D正确.
12、
【答案 】
B;C
【分析】
已知 ,函数定义域为 ,
可得 ,
对于选项 ,易知函数 的图象恒过定点
所以切线斜率 ,切线方程为 ,
显然 不是函数 的切线,故选项A错误;
对于选项 ,当 , 时, , ,
假设存在公切线与 切点 ,
所以函数 在点 处的切线方程为 ,
即 ,
函数 在点 处的切线方程为 ,
即
其满足
所以
此时 ,
整理得 ,
即 ,①
不妨设 ,函数定义域为
可得 ,
当 时, 单调递减;
当 时, 单调递增,
所以 在 上取得极小值也是最小值,
所以 ,
其不满足①式,故 不存在,
所以不存在与函数 、 图象均相切的直线,
故选项B正确;
对于选项 ,当 , 时 , ,
可得
假设存在公切线与 切点 ,
所以函数 在点 处的切线方程为 ,
即
函数 在点 处的切线方程为
即
其满
所以
即 ②
不妨设 函数定义域为 ,
可得
当 时, 单调递增;
当 时, 单调递减,
所以 在 上取得极大值也是最大值,
此时方程②有两解,
所以存在 条公切线,故选项C正确;
对于选项 ,函数 、 至多存在两条公切线,故选项D错误.
故选:BC.
三、填空题
13、
【答案 】
;
【分析】
由题意可知:
,解得 .
故答案为: , .
14、
【答 案】
【分析】
甲以 的比分获胜,甲只能在第 、 、 次中失败 次,第 次获胜,因此所求概率为
15、
【答案 】
【分析】
设 ,
则 ,
从而由 ,
得 ,
故 .
故
16、
【答 案】
【分析】
令 ,即 ,显然 不是方程的根,
则 ,
令 ,
,
, 随 的变化如下表所示:
极小值 极大值
又 , ,
且 时, ,
且 时, ,
当 时, ,
时, ,
做出函数草图如下图所示:
故 ,
即 的取值范围为 .
四、解答题
17、
【答 案】
(1)、
(2)、
【分析】
(1)、以 为坐标原点,分别以 为 , , 轴的正方向,建立空间直角坐标系,则
故 ,
设异面直线 与 所成角为 ,
(2)、设 是平面 的法向量, ,
取 ,有
设 ) 是平面 的法向量,
,
则
取 ,有
设平面 与平面 所成角为 ,
18、
【答 案】
(1)、
暂无
(2)、
暂无
【分析】
(1)、由题意可知:
又
所以相关系数
因为相关系数 ,所以 与 的线性相关性较高,可以利用线性回归模型拟合 与 的关系.
(2)、由( )知
所以
所以
所以 与 的回归直线为
当 时,
即在 的温度下,种子发芽的颗数为 .
19、
【答 案】
(1)、
见解析
(2)、
【分析】
(1)、当 时,
若 , 恒成立,函数 的单调递增区间为
若 , 或 , ,函数 单调递增,
时, ,函数 单调递减
若 , 或 时, ,函数 单调递增,
时, ,函数 单调递减
综上: 时,函数 的单调递增区间为
, 时,函数 的单调递增区间为 ,
函数 的单调递减区间为
时,函数 的单调递增区间为 ,
函数 的单调递减区间为
(2)、 ,即 ,
消元有 ,
解得 或 .
当 时, , ,满足题意
当 时, , ,与存在极值点矛盾
故 , , .
20、
【答案 】
(1)、
见解析
(2)、
见解析
【分析】
(1)、因为该同学踢一次点球命中的概率 ,
由题意, 可能取 , , ,则 , ,
,
的分布列为
即 .
(2)、(i) 第 次触球者是甲的概率记为 ,
则当 时,第 次触球者是甲的概率为 ,第 次触球者不是甲的概率为 ,
则 ,
从而 ,
又 ,
是以 为首项,公比为 的等比数列.
(ii) ,
, ,
,
故第 次触球者是甲的概率大.
21、
【答 案】
(1)、
(2)、
【分析】
(1)、设切点为 ,则切线方程为
切线过点 ,故 ,整理得
令 最大值 ,故
(2)、(i)当 时, 恒成立,函数 在区间 上单调递减,
所以 ,所以 ,
令 ,则函数 在区间 上单调递增,
所以 的最小值为 ,即 的最小值为 .
(ⅱ)当 时,由 ,得 ,由 ,得
所以函数 在区间 上单调递减,在区间 上单调递增
所以
①当 时, ,此时
所以 ,
令 ,则
所以函数 在区间[ 上单调递增,
所以函数 的最小值为
所以 的最小值为
②当 时, ,
所以
所以
令 ,则 ,
所以函数 在区间( 上单调递减,
所
综止所述: 的最小值为
22、
【答案 】
(1)、
(2)、
见解析
【分析】
(1)、记 .
则 恒成立,即 .
∵ ,
当 ,当 ;
∴ 在 上单调递增,在 上单调递减
∴ ,解得 ·
∴实数 的取值范围是
(2)、记
在 上单调递增
令 ,
则 .所以 即 在 上单调递增
由 ,知
∴ 即
∴当 单调递减;当 单调递增.
∴
由(*)式,可得
代入(**)式,得
由(1)知,当 时有 ,故
由 ,
故 ,即 ,原不等式得证
同课章节目录
