2022~2023学年贵州贵阳观山湖区贵阳市第一中学高三上学期期末数学试卷(图片版,含解析)
文档属性
| 名称 | 2022~2023学年贵州贵阳观山湖区贵阳市第一中学高三上学期期末数学试卷(图片版,含解析) |  | |
| 格式 | |||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-01 17:31:44 | ||
图片预览




文档简介
2022~2023学年贵州贵阳观山湖区贵阳市第一中学高三上学期期末数学试
卷
一、单选题(本大题共12小题,每小题5分,共60分)
1、已知集合 , ,则
( )
A.
B.
C.
D.
2、若 ,则“ ”是“ ”的( )
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件
3、在 这四个函数中,当 时,使得不等
式 成立的函数的个数是( )
A.0
B.1
C.2
D.3
4、若A,B,C是△ABC的三个内角,且 ,则下列结论中正确的是( )
A.
B.
C.
D.
5、已知 为 所在平面内一点,若 ,则 ( )
A.1:3
B.1:4
C.1:5
D.1:6
6、深度学习是人工智能的一种具有代表性的实现方法,它是以神经网络为出发点的.在神经网络优化中,指数
衰减的学习率模型为 ,其中 表示每一轮优化时使用的学习率, 表示初始学习率, 表示衰减系
数, 表示训练迭代轮数, 表示衰减速度.已知某个指数衰减的学习率模型的初始学习率为 ,衰减速度为
,且当训练迭代轮数为 时,学习率衰减为 ,则学习率衰减到 以下(不含 )所需的训练迭代轮
数至少为( )(参考数据: , )
A.
B.
C.
D.
7、若圆 上有四个不同的点到直线 的距离为 ,则 的取值范
围是( )
A.
B.
C.
D.
8、一个几何体的三视图如图所示,则该几何体的表面积为( )
A.
B.
C.
D.
9、已知点 是抛物线 上的一点,若以抛物线的焦点 为圆心,以 为半径的圆交抛物线的
准线于 , 两点, ,当 的面积为 时,则 等于( )
A.2
B.
C.4
D.
10、第 届世界大学生夏季运动会于 月 日至 月 日在成都举办,现在从 男 女共 名青年志愿者中,选出
男 女共 名志愿者,安排到编号为 、 、 、 、 的 个赛场,每个赛场只有一名志愿者,其中女志愿者甲不能
安排在编号为 、 的赛场,编号为 的赛场必须安排女志愿者,那么不同安排方案有( )
A. 种
B. 种
C. 种
D. 种
11、已知点 , 分别是双曲线 : 的左、右焦点,过 作斜率为 的直线 与双
曲线的左、右两支分别交于 , 两点,且 ,则双曲线的离心率为( )
A. B. C. D.
12、已知 ,且 ,则 的最大值是( )
A.
B.
C.
D.
二、填空题(本大题共4小题,每小题5分,共20分)
13、已知复数 是纯虚数,其中 , 是虚数单位,则 .
14、在棱长为1的正方体 中,点Q为侧面 内一动点(含边界),若 ,
则点Q的轨迹长度为 .
15、已知点F是椭圆 的右焦点,点P在椭圆上, 且 的最小值为
3,则椭圆C的离心率是 .
16、已知 是定义在R上的函数,且函数 的图象关于直线 对称,当 时,
.若曲线 在 处的切线与函数 的图象也相切,则实数a的值
是 .
三、解答题(本大题共7小题,共70分)
17、(本小题8分)
已知数列 和 满足: , , , ,其中 .
(1)求证: ;
(2)求数列 的前 项和 .
18、(本小题8分)
新型冠状病毒是一种急性的传染性疾病,传播速度很快,它的传播途径主要是飞沫传播、口液传播以及接触传
播等,传播速度最快的是飞沫传播.佩戴口罩能有效预防新冠病毒的感染,双方都戴口罩的情况下新冠病毒感
染的几率大概只有 ,如果戴口罩再加上保持1.8米的距离,感染的几率是 ,如果双方都不戴口罩,那么
感染几率高达 .为了调查不同年龄层的人对“佩戴口罩”的态度,研究人员随机抽取了300人,并将所得结果
统计如下表所示.
年龄
频数 30 75 105 60 30
愿意戴口罩 24 66 90 42 18
(1)完成下列 列联表,并判断是否有 的把握认为年龄与戴口罩态度具有相关性;
年龄在50周岁以上(含50周岁) 年龄在50周岁以下 合计
愿意戴口罩
不愿意戴口罩
合计
(2)现从年龄在50周岁以上(含50周岁)的样本中按是否愿意佩戴口罩,用分层抽样法抽取6人,再从这6人中随
机抽取3人,记抽出的3人中不愿戴口罩的人数为 ,求随机变量 的分布列和数学期望.
参考公式: .
参考数据:
0.050 0.010 0.001
3.841 6.635 10.828
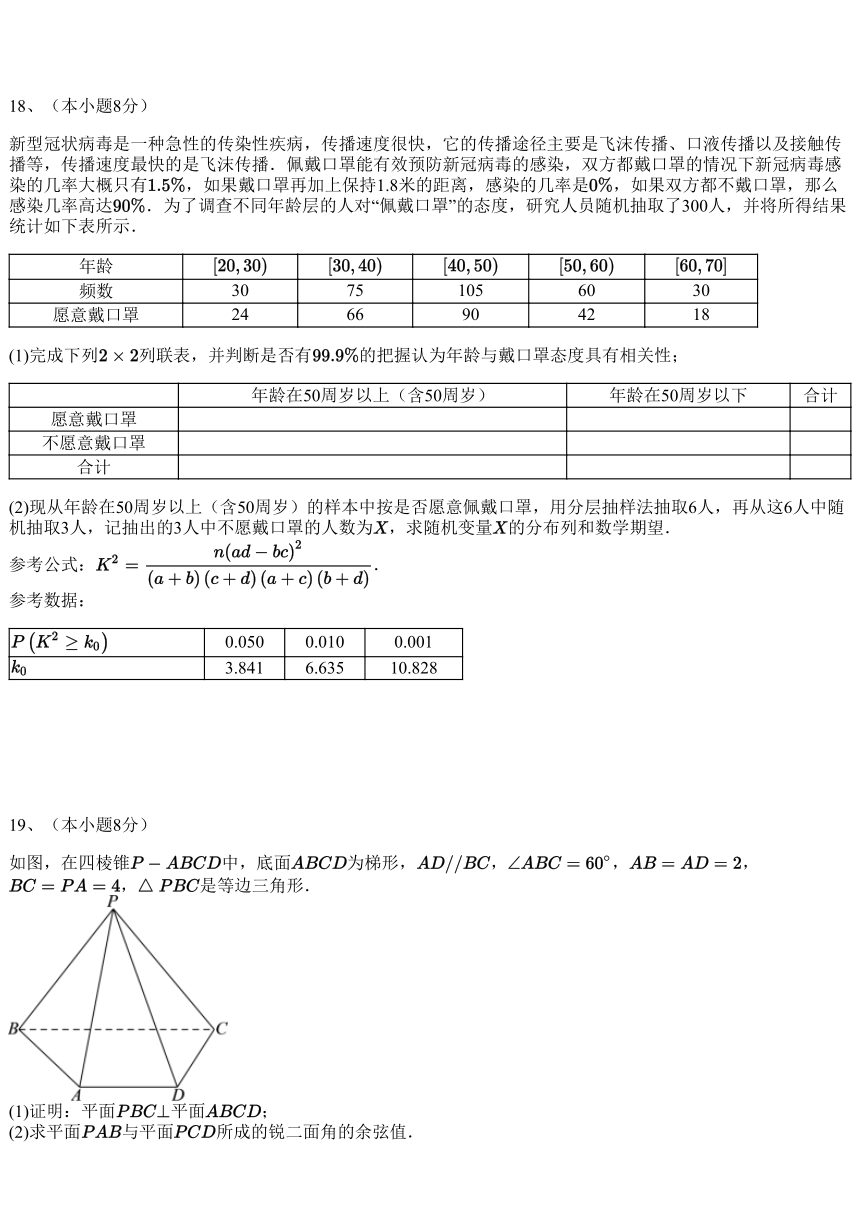
19、(本小题8分)
如图,在四棱锥 中,底面 为梯形, , , ,
, 是等边三角形.
(1)证明:平面 平面 ;
(2)求平面 与平面 所成的锐 二面角的余弦值.
20、(本小题10分)
已知A,B为椭圆 的左、右顶点,P为椭圆上异于A,B的一点,直线AP与直线BP的
斜率之积为 ,且椭圆C过点 .
(1)求椭圆C的标准方程;
(2)若直线AP,BP分别与直 线 相交于M,N两点,且直线BM与椭圆C交于另一点Q,证明:A,N,Q三点
共线.
21、(本小题12分)
已知函数 , , 是 的导数.
(1)讨论 的单调性,并证明: ;
(2)若函数 在区间 内有唯一的零点,求a的取值范围.
22、(本小题12分)
在直角坐标系 中,点 的坐标是 ,曲线 的参数坐标方程 ( 为参数,
).以坐标原点 为极点, 轴正半轴为极轴的极坐标系中曲线 的极坐标方程为 , 与 交于
, 两点.
(1)将曲线 的 极坐标方程化为直角坐标方程,并指出它是什么曲线?
(2)过点 作垂直于 的直线 交 于 , 两点,求 的值.
23、(本小题12分)
已知 、 、 都是正实数.
(1)求证: ;
(2) 若 ,求证: .
参考答案
一、单选题
1、
【答 案】
A
【分析】
根据角的范围及集合的关系即可判断.
【详解】
当 时, ,
当 时, ,
所以 .
故选:A
2、
【答 案】
C
【分析】
当 时可由基本不等式推得 ;当 时解不等式可得 ,则可判定它们之间的逻辑关
系.
【详 解】
当 时由基本不等式可得 ,当且仅当 时取得“=”
当 时,则 ,
可得 即 ,
解得 ;
所以“ ”是“ ”的充要条件.
故选: .
3、
【答 案】
D
【分析】
依题意可得 在 内是上凸函数,结合基本初等函数的图象判断即可.
【详解】
满足 为上凸函数,如图:
分别考虑四个函数在 上的图象,
如下图,因为 在 上是上 凸函数,故正确;
如下图, 在 上不是上凸函数,故错误;
如下图, 在 上是上凸函数,故正确;
如下图, 在 上是上凸函数,故正确;
故选:D.
4、
【答 案】
B
【分析】
由正弦定理、三角形内角及余弦函数性质判断A、B;特殊值 即可判断C、D.
【详解】
由 ,则 ,而 ,则 ,A错;
由 ,结合余弦函数性质知: ,B对;
对于 ,则 , ,C、D错;
故选:B
5、
【答 案】
B
【分析】
取 边中点 ,由已知及向量的线性运算得 ,从而得到两个三角形高的比,可得到答案.
【详解】
由 ,得 ,
取 边中点 ,连接 ,则 ,所以 ,
又 与 有相同的底边 ,则它们的高之比即为 与 的比为 ,
所以 .
故选:B.
6、
【答 案】
C
【分析】
由已知信息可得出 ,将 , 代入指数模型求出 的值,然后解不等式 ,结合
对数运算可求得结果.
【详解】
由题中信息可得 , ,则 ,
当 时, ,即 ,解得 ,即 ,
由 ,可得 ,
所以, ,
故学习率衰减到 以下(不含 )所需的训练迭代轮数至少为 .
故选:C.
7、
【答 案】
C
【分析】
求出与直线 平行且到直线 的距离为 的直线的方程分别为 、 ,由题
意可知,这两条直线与圆 都相交,根据直线与圆的位置关系可得出关于实数 的不等式组,即可解得实数 的
取值范围.
【详解】
将圆 的方 程化为标准方程为 ,圆心为 ,半径为 ,
设与直线 平行且到直线 的距离为 的直线的方程为 ,
则 ,解得 或 ,
所以,直线 、 均与圆 相交,
所以, ,解得 ,
因此,实数 的取值范围是 .
故选:C.
8、
【答 案】
A
【分析】
作出对应的立体图形,求出各边长和 的正弦值,即可求出该几何体的表面积.
【详解】
由题意, 作出立体图形如下图所示,
过点 作 于点 ,
由几何知识得,
,
在 中,由勾股定理得,
,
在 中,由勾股定理 得,
,
在Rt 中,由勾股定理得 ,
在 中,由勾股定 理得,
在 中,由余弦定理得,
,解得: ,
∴ ,
故选:A.
9、
【答 案】
C
【分析】
依题意可得 为等边三角形,则用 可表示出 ,利用三角形面积公式,结合抛物线定义可构造
方程求得 的值.
【详解】
依题意 ,所以 为等边三角形,
设准线与 轴交点为 ,则 , ,
则圆的半径 ,
,解得 (负值舍去).
故选:C.
10、
【答案 】
D
【分析】
对女志愿者甲是否被选中进行分类讨论,分别确定各赛场的人员安排,结合分类加法计数原理可得结果.
【详解】
分以下两 种情况讨论:
①女志愿者甲被选中,则 还需从剩余的 人中选出 男 女,选法种数为 ,
则女志愿者甲可安排在 号或 号或 号赛场,另一位女志愿者安排在 号赛场,
余下 个男志愿者随意安排,此时,不同的安排种数为 ;
②女志愿者甲没被选中,则还需从剩余 人中选出 男 女,选法种数为 ,
编号为 的赛场必须安排女志愿者,只需从 名女志愿者中抽 人安排在 号赛场,
余下 人可随意安排,此时,不同的安排方法种数为 .
由分类加法计数原理可知,不同的安排方法种数为 种 .
故选:D.
11、
【答 案】
暂无
【分析】
略
12、
【答 案】
A
【分析】
根据余弦函数、正切函数的性质可得当 取最小值时 取最大值,则问题转化为求出 的最小值,依
题意利用两角和的正弦公式及同角三角函数的基本关系得到 ,再结合二次函数的性
质求出 的最小值,最后根据同角三角函数的基本关系计算可得.
【详解】
因为 ,所以 ,
所以 ,
因为 ,则 , ,
且 在 上单调递减, 在 上单调递增,
要使 取最大值,只需 取最小值,
所以
,
因为 ,所以 ,
所以当 时 ,
此时 ,解得 或 (舍去),
所以 .
故选:A
二、填空题
13、
【答案 】
【分析】
利用复数的概念可得出关于实数 的不等式与等式,解出 的值,可得出复数 ,再利用复数的除法可化简复数
.
【详解】
因为复数 是纯虚数,其中 ,则 ,解得 ,
所以, ,因此, .
故答案为: .
14、
【答 案】
/
【分析】
根据题设描述确定Q的轨迹,即可求其长度.
【详解】
由题意, 在面 的轨迹是以 为圆心,半径为 的四分之一圆弧,
所以轨迹长度为 .
故答案为:
15、
【答案 】
【分析】
若 是椭圆左焦点,数形结合及椭圆定义可得 ,结合已知和两点距离公式求椭圆参
数,进而可得离心率.
【详解】
由 ,则 在椭圆内,若 是椭圆左焦点,
所以 ,
仅当 共线且 在 之间时取等号,故 ,即 ,
而 且 ,则 ,故 ,
此时 ,故 .
故答案为:
16、
【答 案】
【分析】
先根据函数 的对称性得 的对称性,进一步求出函数的解析式,利用导数的几何意义建立方程求
解即可.
【详解】
因为函数 的图象关于直线 对称,所以 ,
即 ,所以函数 关于 对称,
当 ,即 时, ,则 ,所以 ,
故函数 在 处的切线为 ,即 ,
设直线 与 相切于点 ,因为 ,所以 ,
所以 ,所以 .
故答案为:
三、解答题
17、
【答案 】
(1)证明见解析
(2)
【分析】
(1)由已知条件可推导出数列 为常数列,数列 为等比数列,求出这两个数列的通项公式,
可求得数列 的通项公式,即可证得 成立;
(2)由(1)可得出数列 的通项公式,利用分组求和法可求得 .
【详解】
(1)证明:因为 ①, ②,
① ②可得 ,且 ,
所以,数列 为常数列,且 ③,
① ②可得 ,且 ,
所以,数列 为等比数列,且该数列的首项为 ,公比为 ,
所以, ④,
③ ④可得 ,则 ,
所以, .
(2)解:由(1)可知, ,
则
.
18、
【答 案】
(1)列联表见解析,有 的把握认为年龄与戴口罩态度具有相关性
(2)分布列见解析,
【分析】
(1)根据频数分布表完善列联表,计算出卡方,即可得解;
(2)首先利用分层抽样求出愿意、不愿意戴口罩的人数,则 的可能取值为 、 、 ,求出所对应的概率,即
可得到分布列与数学期望.
【详解】
(1)依题 意可得 列联表如下:
年龄在50周岁以上(含50周岁) 年龄在50周岁以下 合计
愿意戴口罩 60 180 240
不愿意戴口罩 30 30 60
合计 90 210 300
,
故有 的把握认为年龄与戴口罩态度具有相关性;
(2)年龄在50周岁以上(含50周岁)愿意戴口罩的抽取 人,不愿意戴口罩的抽取 人,
则 的可能取值为 、 、 ,
所以 , , ,
所以 的分布列为:
则 .
19、
【答 案】
(1)证明见解析
(2)
【分析】
(1)取线段 的中点 ,连接 、 ,证明出 平面 ,利用面面垂直的判定定理可证得结论成
立;
(2)连接 ,取线段 的中点 ,连接 ,证明出 ,以点 为坐标原点, 、 、 的方向
分别为 、 、 轴的正方向建立空间直角坐标系,利用空间向量法可求得平面 与平面 所成的锐二面角
的余弦值.
【详解】
(1)证明 :取线段 的中点 ,连接 、 ,
因为 是等边三角形,且 , 为 的中点,所以, ,
且 ,
因为 , , ,则 为等边三角形,
所以, ,
又因为 ,所 以, ,所以, ,
因为 , 、 平面 ,所以, 平面 ,
因为 平面 ,因此,平面 平面 .
(2)解:连接 ,取线段 的中点 ,连接 ,
因为 ,则 ,
又因为 ,故 为等边三角 形,
因为 为 的中点,所以, ,
又因为 平面 ,以点 为坐标原点, 、 、 的方向分别为 、 、 轴的正方向建立如下图所
示的空间直角坐标系,
则 、 、 、 、 ,
设平面 的法向量为 , , ,
由 ,取 ,则 ,
设平面 的法向量为 , , ,
由 ,取 ,可得 ,
因为 ,
因此,平面 与平面 所成的锐二面角的余弦值为 .
20、
【答 案】
(1)
(2)证明见解析
【分析】
(1)令 ,根据斜率之积及 可得 ,结合点在椭圆上求椭圆参数,即可得椭圆方
程;
(2)由题意,设 ,则 ,写出M,N两点坐标,求直线BM,联立椭圆求点Q坐
标,两点法判断 是否成立,即可证结论.
【详解】
(1)令 ,则 ,又 ,则 ,
所以 ,即 , ,
由 在椭圆上,则 ,
联立以上两式,可得 ,故椭圆C的标准方程为 .
(2)由题设,直线 、 斜率存在且不为0, ,
令 ,则 ,故 , ,
所以 ,联立 ,整理得 ,
显然 ,则 ,则 ,
由 , ,即 ,
所以A,N,Q三点共线.
21、
【答案 】
(1)答案见解析
(2)
【分析】
(1)求出导函数,根据 , 分类讨论即可,构造函数,利用导数法求解最值即可证明;
(2)把问题转化为方程 在区间 内有唯一解,构造函数,利用导数研究单调 性,数形结
合即可求解.
【详解】
(1)因为 ,所以 ,
当 时, ,则 在 上单调递增,
当 时,令 得 ,令 得 ,
所以函数 的增区间为 ,减区间为 ,
令 ,则 ,令 得 ,
令 得 ,所以函数 的增区间为 ,减 区间为 ,
所以当 时, 取得最小值为 ,
所以 ,得证;
(2)由(1)知, ,
因为函数 在区间 内有唯一的零点 ,所以方程 在区间 内有唯一解,
令 ,则函数 与 在 上只有一个交点,
记 ,则 ,所以 在 上单调递增,
所以 ,即 ,
故 ,
所以 在 上单调递增,又 ,
如图:
要使方程 在区间 内有唯一解,则 .
所以a的取值范围是 .
【点睛】
方法点睛: 导函数中常用的两种常用的转化方法:
一是利用导数研究含参函数的单调性,常化为不等 式恒成立问题.注意分类讨论与数形结合思想的应用;
二是函数的零点、不等式证明常转化为函数的单调性、极(最)值问题处理.
22、
【答 案】
(1) ,焦点为 ,顶点为 的抛物线(顶点除外).
(2)
【分析】
(1)利用极坐标与直角坐标的互化公式,可得曲线 的直角坐标方程;
(2)将曲线 的参数方程代入曲线 的直角坐标方程,利用直线参数方 程中参数的几何意义求出
、同理得到 ,即可得解.
【详解】
(1)因为曲线 的极坐标方程为 ,
所以 ,又 ,所以 ,则 ,
所以 ,即 ,
因为 ,即 ,所以 ,
所以曲线 的直角坐标方程为 ,
曲线 可以由抛物线 向下平移 个单位得到,
所以曲线 为焦点为 ,顶点为 的抛物线(顶点除外).
(2)将 代入 得 ,
设 , 对应的参数分别为 , , ,
所以 ,
过点 作垂直于 的直线 的参数方程为 ( 为参数, ),
将 代入 得 ,
设 , 对应的参数分别为 , , ,
所以 ,
所以 .
23、
【答案 】
(1)证明见解析
(2)证明见解析
【分析】
(1)利用基本不等式可得出 , , ,结合不等式的基本性质可证得结
论成立;
(2)由已知等式可得出 ,利用柯西不等式可得出 ,再利用作商法可证
得结论成立.
【详解】
(1)证明 :因为 、 、 都是正实数,
由基本不等式可得 , , ,
由不等式的基本性质可得 ,
所以, ,
当且仅当 时,等号成立,故 .
(2)证明:等式 两边同时除以 可得 ,
由柯西不等式可得 ,
当且仅当 时,等号成立,故 ,
所以, ,故 .
卷
一、单选题(本大题共12小题,每小题5分,共60分)
1、已知集合 , ,则
( )
A.
B.
C.
D.
2、若 ,则“ ”是“ ”的( )
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件
3、在 这四个函数中,当 时,使得不等
式 成立的函数的个数是( )
A.0
B.1
C.2
D.3
4、若A,B,C是△ABC的三个内角,且 ,则下列结论中正确的是( )
A.
B.
C.
D.
5、已知 为 所在平面内一点,若 ,则 ( )
A.1:3
B.1:4
C.1:5
D.1:6
6、深度学习是人工智能的一种具有代表性的实现方法,它是以神经网络为出发点的.在神经网络优化中,指数
衰减的学习率模型为 ,其中 表示每一轮优化时使用的学习率, 表示初始学习率, 表示衰减系
数, 表示训练迭代轮数, 表示衰减速度.已知某个指数衰减的学习率模型的初始学习率为 ,衰减速度为
,且当训练迭代轮数为 时,学习率衰减为 ,则学习率衰减到 以下(不含 )所需的训练迭代轮
数至少为( )(参考数据: , )
A.
B.
C.
D.
7、若圆 上有四个不同的点到直线 的距离为 ,则 的取值范
围是( )
A.
B.
C.
D.
8、一个几何体的三视图如图所示,则该几何体的表面积为( )
A.
B.
C.
D.
9、已知点 是抛物线 上的一点,若以抛物线的焦点 为圆心,以 为半径的圆交抛物线的
准线于 , 两点, ,当 的面积为 时,则 等于( )
A.2
B.
C.4
D.
10、第 届世界大学生夏季运动会于 月 日至 月 日在成都举办,现在从 男 女共 名青年志愿者中,选出
男 女共 名志愿者,安排到编号为 、 、 、 、 的 个赛场,每个赛场只有一名志愿者,其中女志愿者甲不能
安排在编号为 、 的赛场,编号为 的赛场必须安排女志愿者,那么不同安排方案有( )
A. 种
B. 种
C. 种
D. 种
11、已知点 , 分别是双曲线 : 的左、右焦点,过 作斜率为 的直线 与双
曲线的左、右两支分别交于 , 两点,且 ,则双曲线的离心率为( )
A. B. C. D.
12、已知 ,且 ,则 的最大值是( )
A.
B.
C.
D.
二、填空题(本大题共4小题,每小题5分,共20分)
13、已知复数 是纯虚数,其中 , 是虚数单位,则 .
14、在棱长为1的正方体 中,点Q为侧面 内一动点(含边界),若 ,
则点Q的轨迹长度为 .
15、已知点F是椭圆 的右焦点,点P在椭圆上, 且 的最小值为
3,则椭圆C的离心率是 .
16、已知 是定义在R上的函数,且函数 的图象关于直线 对称,当 时,
.若曲线 在 处的切线与函数 的图象也相切,则实数a的值
是 .
三、解答题(本大题共7小题,共70分)
17、(本小题8分)
已知数列 和 满足: , , , ,其中 .
(1)求证: ;
(2)求数列 的前 项和 .
18、(本小题8分)
新型冠状病毒是一种急性的传染性疾病,传播速度很快,它的传播途径主要是飞沫传播、口液传播以及接触传
播等,传播速度最快的是飞沫传播.佩戴口罩能有效预防新冠病毒的感染,双方都戴口罩的情况下新冠病毒感
染的几率大概只有 ,如果戴口罩再加上保持1.8米的距离,感染的几率是 ,如果双方都不戴口罩,那么
感染几率高达 .为了调查不同年龄层的人对“佩戴口罩”的态度,研究人员随机抽取了300人,并将所得结果
统计如下表所示.
年龄
频数 30 75 105 60 30
愿意戴口罩 24 66 90 42 18
(1)完成下列 列联表,并判断是否有 的把握认为年龄与戴口罩态度具有相关性;
年龄在50周岁以上(含50周岁) 年龄在50周岁以下 合计
愿意戴口罩
不愿意戴口罩
合计
(2)现从年龄在50周岁以上(含50周岁)的样本中按是否愿意佩戴口罩,用分层抽样法抽取6人,再从这6人中随
机抽取3人,记抽出的3人中不愿戴口罩的人数为 ,求随机变量 的分布列和数学期望.
参考公式: .
参考数据:
0.050 0.010 0.001
3.841 6.635 10.828
19、(本小题8分)
如图,在四棱锥 中,底面 为梯形, , , ,
, 是等边三角形.
(1)证明:平面 平面 ;
(2)求平面 与平面 所成的锐 二面角的余弦值.
20、(本小题10分)
已知A,B为椭圆 的左、右顶点,P为椭圆上异于A,B的一点,直线AP与直线BP的
斜率之积为 ,且椭圆C过点 .
(1)求椭圆C的标准方程;
(2)若直线AP,BP分别与直 线 相交于M,N两点,且直线BM与椭圆C交于另一点Q,证明:A,N,Q三点
共线.
21、(本小题12分)
已知函数 , , 是 的导数.
(1)讨论 的单调性,并证明: ;
(2)若函数 在区间 内有唯一的零点,求a的取值范围.
22、(本小题12分)
在直角坐标系 中,点 的坐标是 ,曲线 的参数坐标方程 ( 为参数,
).以坐标原点 为极点, 轴正半轴为极轴的极坐标系中曲线 的极坐标方程为 , 与 交于
, 两点.
(1)将曲线 的 极坐标方程化为直角坐标方程,并指出它是什么曲线?
(2)过点 作垂直于 的直线 交 于 , 两点,求 的值.
23、(本小题12分)
已知 、 、 都是正实数.
(1)求证: ;
(2) 若 ,求证: .
参考答案
一、单选题
1、
【答 案】
A
【分析】
根据角的范围及集合的关系即可判断.
【详解】
当 时, ,
当 时, ,
所以 .
故选:A
2、
【答 案】
C
【分析】
当 时可由基本不等式推得 ;当 时解不等式可得 ,则可判定它们之间的逻辑关
系.
【详 解】
当 时由基本不等式可得 ,当且仅当 时取得“=”
当 时,则 ,
可得 即 ,
解得 ;
所以“ ”是“ ”的充要条件.
故选: .
3、
【答 案】
D
【分析】
依题意可得 在 内是上凸函数,结合基本初等函数的图象判断即可.
【详解】
满足 为上凸函数,如图:
分别考虑四个函数在 上的图象,
如下图,因为 在 上是上 凸函数,故正确;
如下图, 在 上不是上凸函数,故错误;
如下图, 在 上是上凸函数,故正确;
如下图, 在 上是上凸函数,故正确;
故选:D.
4、
【答 案】
B
【分析】
由正弦定理、三角形内角及余弦函数性质判断A、B;特殊值 即可判断C、D.
【详解】
由 ,则 ,而 ,则 ,A错;
由 ,结合余弦函数性质知: ,B对;
对于 ,则 , ,C、D错;
故选:B
5、
【答 案】
B
【分析】
取 边中点 ,由已知及向量的线性运算得 ,从而得到两个三角形高的比,可得到答案.
【详解】
由 ,得 ,
取 边中点 ,连接 ,则 ,所以 ,
又 与 有相同的底边 ,则它们的高之比即为 与 的比为 ,
所以 .
故选:B.
6、
【答 案】
C
【分析】
由已知信息可得出 ,将 , 代入指数模型求出 的值,然后解不等式 ,结合
对数运算可求得结果.
【详解】
由题中信息可得 , ,则 ,
当 时, ,即 ,解得 ,即 ,
由 ,可得 ,
所以, ,
故学习率衰减到 以下(不含 )所需的训练迭代轮数至少为 .
故选:C.
7、
【答 案】
C
【分析】
求出与直线 平行且到直线 的距离为 的直线的方程分别为 、 ,由题
意可知,这两条直线与圆 都相交,根据直线与圆的位置关系可得出关于实数 的不等式组,即可解得实数 的
取值范围.
【详解】
将圆 的方 程化为标准方程为 ,圆心为 ,半径为 ,
设与直线 平行且到直线 的距离为 的直线的方程为 ,
则 ,解得 或 ,
所以,直线 、 均与圆 相交,
所以, ,解得 ,
因此,实数 的取值范围是 .
故选:C.
8、
【答 案】
A
【分析】
作出对应的立体图形,求出各边长和 的正弦值,即可求出该几何体的表面积.
【详解】
由题意, 作出立体图形如下图所示,
过点 作 于点 ,
由几何知识得,
,
在 中,由勾股定理得,
,
在 中,由勾股定理 得,
,
在Rt 中,由勾股定理得 ,
在 中,由勾股定 理得,
在 中,由余弦定理得,
,解得: ,
∴ ,
故选:A.
9、
【答 案】
C
【分析】
依题意可得 为等边三角形,则用 可表示出 ,利用三角形面积公式,结合抛物线定义可构造
方程求得 的值.
【详解】
依题意 ,所以 为等边三角形,
设准线与 轴交点为 ,则 , ,
则圆的半径 ,
,解得 (负值舍去).
故选:C.
10、
【答案 】
D
【分析】
对女志愿者甲是否被选中进行分类讨论,分别确定各赛场的人员安排,结合分类加法计数原理可得结果.
【详解】
分以下两 种情况讨论:
①女志愿者甲被选中,则 还需从剩余的 人中选出 男 女,选法种数为 ,
则女志愿者甲可安排在 号或 号或 号赛场,另一位女志愿者安排在 号赛场,
余下 个男志愿者随意安排,此时,不同的安排种数为 ;
②女志愿者甲没被选中,则还需从剩余 人中选出 男 女,选法种数为 ,
编号为 的赛场必须安排女志愿者,只需从 名女志愿者中抽 人安排在 号赛场,
余下 人可随意安排,此时,不同的安排方法种数为 .
由分类加法计数原理可知,不同的安排方法种数为 种 .
故选:D.
11、
【答 案】
暂无
【分析】
略
12、
【答 案】
A
【分析】
根据余弦函数、正切函数的性质可得当 取最小值时 取最大值,则问题转化为求出 的最小值,依
题意利用两角和的正弦公式及同角三角函数的基本关系得到 ,再结合二次函数的性
质求出 的最小值,最后根据同角三角函数的基本关系计算可得.
【详解】
因为 ,所以 ,
所以 ,
因为 ,则 , ,
且 在 上单调递减, 在 上单调递增,
要使 取最大值,只需 取最小值,
所以
,
因为 ,所以 ,
所以当 时 ,
此时 ,解得 或 (舍去),
所以 .
故选:A
二、填空题
13、
【答案 】
【分析】
利用复数的概念可得出关于实数 的不等式与等式,解出 的值,可得出复数 ,再利用复数的除法可化简复数
.
【详解】
因为复数 是纯虚数,其中 ,则 ,解得 ,
所以, ,因此, .
故答案为: .
14、
【答 案】
/
【分析】
根据题设描述确定Q的轨迹,即可求其长度.
【详解】
由题意, 在面 的轨迹是以 为圆心,半径为 的四分之一圆弧,
所以轨迹长度为 .
故答案为:
15、
【答案 】
【分析】
若 是椭圆左焦点,数形结合及椭圆定义可得 ,结合已知和两点距离公式求椭圆参
数,进而可得离心率.
【详解】
由 ,则 在椭圆内,若 是椭圆左焦点,
所以 ,
仅当 共线且 在 之间时取等号,故 ,即 ,
而 且 ,则 ,故 ,
此时 ,故 .
故答案为:
16、
【答 案】
【分析】
先根据函数 的对称性得 的对称性,进一步求出函数的解析式,利用导数的几何意义建立方程求
解即可.
【详解】
因为函数 的图象关于直线 对称,所以 ,
即 ,所以函数 关于 对称,
当 ,即 时, ,则 ,所以 ,
故函数 在 处的切线为 ,即 ,
设直线 与 相切于点 ,因为 ,所以 ,
所以 ,所以 .
故答案为:
三、解答题
17、
【答案 】
(1)证明见解析
(2)
【分析】
(1)由已知条件可推导出数列 为常数列,数列 为等比数列,求出这两个数列的通项公式,
可求得数列 的通项公式,即可证得 成立;
(2)由(1)可得出数列 的通项公式,利用分组求和法可求得 .
【详解】
(1)证明:因为 ①, ②,
① ②可得 ,且 ,
所以,数列 为常数列,且 ③,
① ②可得 ,且 ,
所以,数列 为等比数列,且该数列的首项为 ,公比为 ,
所以, ④,
③ ④可得 ,则 ,
所以, .
(2)解:由(1)可知, ,
则
.
18、
【答 案】
(1)列联表见解析,有 的把握认为年龄与戴口罩态度具有相关性
(2)分布列见解析,
【分析】
(1)根据频数分布表完善列联表,计算出卡方,即可得解;
(2)首先利用分层抽样求出愿意、不愿意戴口罩的人数,则 的可能取值为 、 、 ,求出所对应的概率,即
可得到分布列与数学期望.
【详解】
(1)依题 意可得 列联表如下:
年龄在50周岁以上(含50周岁) 年龄在50周岁以下 合计
愿意戴口罩 60 180 240
不愿意戴口罩 30 30 60
合计 90 210 300
,
故有 的把握认为年龄与戴口罩态度具有相关性;
(2)年龄在50周岁以上(含50周岁)愿意戴口罩的抽取 人,不愿意戴口罩的抽取 人,
则 的可能取值为 、 、 ,
所以 , , ,
所以 的分布列为:
则 .
19、
【答 案】
(1)证明见解析
(2)
【分析】
(1)取线段 的中点 ,连接 、 ,证明出 平面 ,利用面面垂直的判定定理可证得结论成
立;
(2)连接 ,取线段 的中点 ,连接 ,证明出 ,以点 为坐标原点, 、 、 的方向
分别为 、 、 轴的正方向建立空间直角坐标系,利用空间向量法可求得平面 与平面 所成的锐二面角
的余弦值.
【详解】
(1)证明 :取线段 的中点 ,连接 、 ,
因为 是等边三角形,且 , 为 的中点,所以, ,
且 ,
因为 , , ,则 为等边三角形,
所以, ,
又因为 ,所 以, ,所以, ,
因为 , 、 平面 ,所以, 平面 ,
因为 平面 ,因此,平面 平面 .
(2)解:连接 ,取线段 的中点 ,连接 ,
因为 ,则 ,
又因为 ,故 为等边三角 形,
因为 为 的中点,所以, ,
又因为 平面 ,以点 为坐标原点, 、 、 的方向分别为 、 、 轴的正方向建立如下图所
示的空间直角坐标系,
则 、 、 、 、 ,
设平面 的法向量为 , , ,
由 ,取 ,则 ,
设平面 的法向量为 , , ,
由 ,取 ,可得 ,
因为 ,
因此,平面 与平面 所成的锐二面角的余弦值为 .
20、
【答 案】
(1)
(2)证明见解析
【分析】
(1)令 ,根据斜率之积及 可得 ,结合点在椭圆上求椭圆参数,即可得椭圆方
程;
(2)由题意,设 ,则 ,写出M,N两点坐标,求直线BM,联立椭圆求点Q坐
标,两点法判断 是否成立,即可证结论.
【详解】
(1)令 ,则 ,又 ,则 ,
所以 ,即 , ,
由 在椭圆上,则 ,
联立以上两式,可得 ,故椭圆C的标准方程为 .
(2)由题设,直线 、 斜率存在且不为0, ,
令 ,则 ,故 , ,
所以 ,联立 ,整理得 ,
显然 ,则 ,则 ,
由 , ,即 ,
所以A,N,Q三点共线.
21、
【答案 】
(1)答案见解析
(2)
【分析】
(1)求出导函数,根据 , 分类讨论即可,构造函数,利用导数法求解最值即可证明;
(2)把问题转化为方程 在区间 内有唯一解,构造函数,利用导数研究单调 性,数形结
合即可求解.
【详解】
(1)因为 ,所以 ,
当 时, ,则 在 上单调递增,
当 时,令 得 ,令 得 ,
所以函数 的增区间为 ,减区间为 ,
令 ,则 ,令 得 ,
令 得 ,所以函数 的增区间为 ,减 区间为 ,
所以当 时, 取得最小值为 ,
所以 ,得证;
(2)由(1)知, ,
因为函数 在区间 内有唯一的零点 ,所以方程 在区间 内有唯一解,
令 ,则函数 与 在 上只有一个交点,
记 ,则 ,所以 在 上单调递增,
所以 ,即 ,
故 ,
所以 在 上单调递增,又 ,
如图:
要使方程 在区间 内有唯一解,则 .
所以a的取值范围是 .
【点睛】
方法点睛: 导函数中常用的两种常用的转化方法:
一是利用导数研究含参函数的单调性,常化为不等 式恒成立问题.注意分类讨论与数形结合思想的应用;
二是函数的零点、不等式证明常转化为函数的单调性、极(最)值问题处理.
22、
【答 案】
(1) ,焦点为 ,顶点为 的抛物线(顶点除外).
(2)
【分析】
(1)利用极坐标与直角坐标的互化公式,可得曲线 的直角坐标方程;
(2)将曲线 的参数方程代入曲线 的直角坐标方程,利用直线参数方 程中参数的几何意义求出
、同理得到 ,即可得解.
【详解】
(1)因为曲线 的极坐标方程为 ,
所以 ,又 ,所以 ,则 ,
所以 ,即 ,
因为 ,即 ,所以 ,
所以曲线 的直角坐标方程为 ,
曲线 可以由抛物线 向下平移 个单位得到,
所以曲线 为焦点为 ,顶点为 的抛物线(顶点除外).
(2)将 代入 得 ,
设 , 对应的参数分别为 , , ,
所以 ,
过点 作垂直于 的直线 的参数方程为 ( 为参数, ),
将 代入 得 ,
设 , 对应的参数分别为 , , ,
所以 ,
所以 .
23、
【答案 】
(1)证明见解析
(2)证明见解析
【分析】
(1)利用基本不等式可得出 , , ,结合不等式的基本性质可证得结
论成立;
(2)由已知等式可得出 ,利用柯西不等式可得出 ,再利用作商法可证
得结论成立.
【详解】
(1)证明 :因为 、 、 都是正实数,
由基本不等式可得 , , ,
由不等式的基本性质可得 ,
所以, ,
当且仅当 时,等号成立,故 .
(2)证明:等式 两边同时除以 可得 ,
由柯西不等式可得 ,
当且仅当 时,等号成立,故 ,
所以, ,故 .
同课章节目录
