2022~2023学年河南信阳高三期末理科数学试卷(普通高中 第二次教学质量检测)(PDF版含解析)
文档属性
| 名称 | 2022~2023学年河南信阳高三期末理科数学试卷(普通高中 第二次教学质量检测)(PDF版含解析) |  | |
| 格式 | |||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-31 14:28:15 | ||
图片预览



文档简介
2022~2023学年河南信阳高三期末理科数学试卷(普通高中 第二次教学质
量检测)
一、单选题(本大题共12小题,每小题5分,共60分)
1、已知集合 , ,那么 等于( )
A.
B.
C.
D.
2、下列命题中,错误的命题有( )
A.函数 与 不是同一个函数
B.命题“ , ”的否定为“ , ”
C.设函数 ,则 在 上单调递增
D.设 ,则 “ ”是“ ”的必要不充分条件
3、已知角 的终边在直线 上,则 ( )
A.
B.
C.1
D.
4、在等差数列 中, , ,则 ( )
A.19
B.18
C.17
D.20
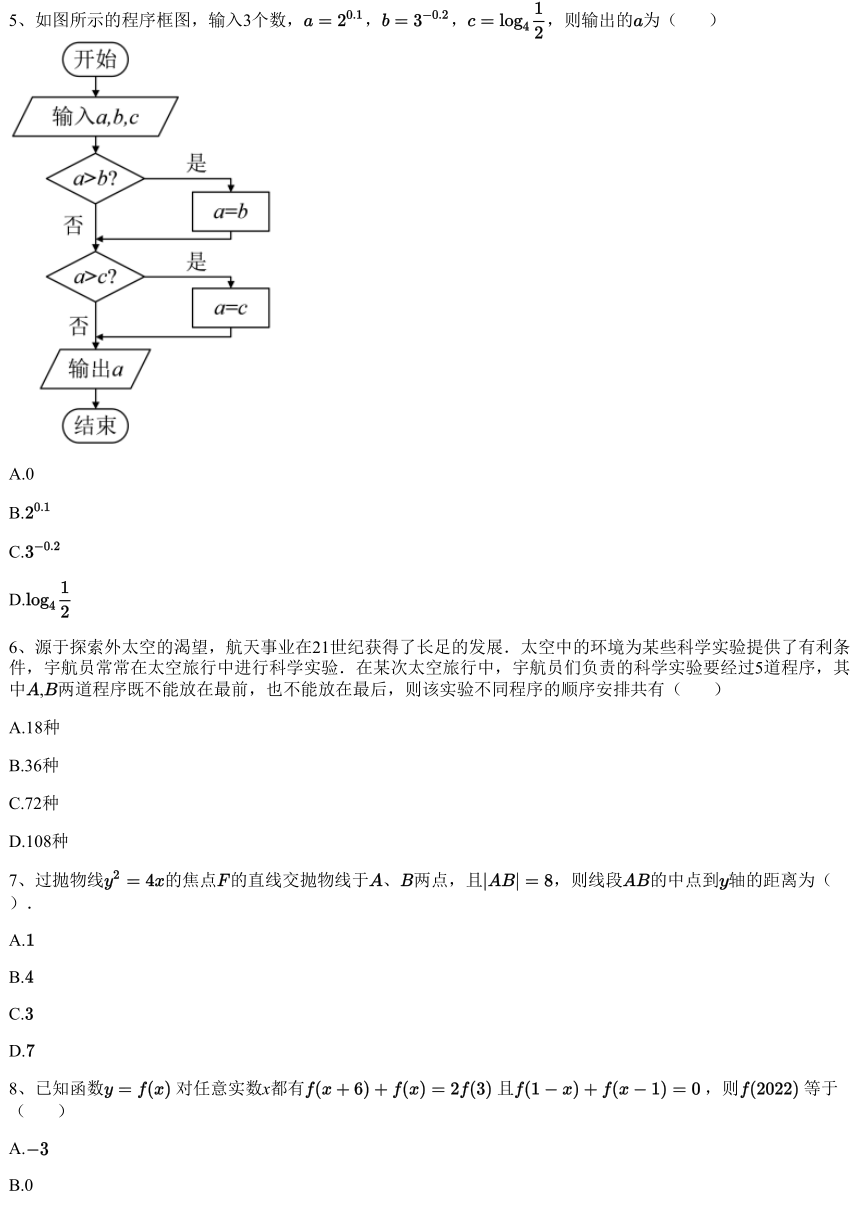
5、如图所示的程序框图,输入3个数, , , ,则输出的 为( )
A.0
B.
C.
D.
6、源于探索外太空的渴望,航天事业在21世纪获得了长足的发展.太空中的环境为某些科学实验提供了有利条
件,宇航员常常在太空旅行中进行科学实验.在某次太空旅行中,宇航员们负责的科学实验要经过5道程序,其
中 , 两道程序既不能放在最前,也不能放在最后,则该实验不同程序的顺序安排共有( )
A.18种
B.36种
C.72种
D.108种
7、过抛物线 的焦点 的直线交抛物线于 、 两点,且 ,则线段 的中点到 轴的距离为(
).
A.
B.
C.
D.
8、已知函数 对任意实数x都有 且 ,则 等于
( )
A.
B.0
C.3
D.6
9、已知函数 在区间 上是增函数,且在区间
上恰好取得一次最大值,则 的取值范围是( )
A.
B.
C.
D.
10、某车间加工同一型号零件,第一 二台车床加工的零件分别占总数的40%,60%,各自产品中的次品率分别
为6%,5%.记“任取一个零件为第i台车床加工 ”为事件 ,“任取一个零件是次品”为事件B,则( )
① ② ③ ④
A.①②④
B.②③④
C.②③
D.①②③④
11、设直线 与双曲线 的两条渐近线分别交于点A,B,若点
满足 ,则该双曲线的离心率是( )
A.
B.
C.
D.
12、已知关于 的不等式 对任意 恒成立,则 的最大值为( )
A.
B.1
C.
D.
二、填空题(本大题共4小题,每小题5分,共20分)
13、 是虚数单位,若复数 是纯虚数,则实数 的值为 .
14、 的展开式中 的系数为 .
15、已知 是 内部(不含边界)一点,若 , ,则
.
16、剪纸是一种镂空艺术,是中国汉族最古老的民间艺术之一.如图,一圆形纸片,直径 cm,需要剪去
菱形 ,可以经过两次对折、沿 裁剪、展开后得到.若 ,要使镂空的菱形 面积最大,
则菱形的边长 cm.
三、解答题(本大题共7小题,共70分)
17、(本小题8分)
在 中,角A,B,C的对边分别为a,b,c,且 .
(1)求B的大小;
(2)若 ,求 的面积.
18、(本小题8分)
2022年北京冬奥会即第24届冬季奥林匹克运动会在2022年2月4日至2月20日在北京和张家口举行.某研究机构为
了解大学生对冰壶运动是否有兴趣,从某大学随机抽取男生、女生各200人,对冰壶运动有兴趣的人数占总数的
,女生中有80人对冰壶运动没有兴趣.
有兴趣没有兴趣合计
男
女 80
合计
(1)完成上面2×2列联表,并判断是否有99%的把握认为对冰壶运动是否有兴趣与性别有关?
(2)按性别用分层抽样的方法从对冰壶运动有兴趣的学生中抽取9人,若从这9人中随机选出2 人作为冰壶运动的
宣传员,设X表示选出的2人中女生的人数,求X的分布列和数学期望.
附: .
0.100 0.050 0.025 0.010 0.001
2.706 3.841 5.024 6.635 10.828
19、(本小题8分)
在数列{an}中, (n∈N*), .
(1) 求 ;
(2)设 为 的前n项和,求 的最小值.
20、(本小题10分)
已知椭圆 长轴的两个端点分别为 ,离心率为 .
(1)求椭圆 的方程;
(2) 为椭圆 上异于 的动点,直线 分别交直线 于 两点,连接 并延长交椭圆 于
点 .
(ⅰ)求 证:直线 的斜率之积为定值;
(ⅱ)判断 三点是否共线,并说明理由 .
21、(本小题12分)
已知函数 e .
(1)若函数 在 上单调递增,求实 数 的取值范围;
(2)设函数 ,若 ,求 的值.
22、(本小题12分)
在平面直角坐标系 中,曲线 的参数方程为: ( 为参数),在以 为极点, 轴的非
负半轴为极轴的极坐标系中,点 的极坐标为 .
(1)写出曲线 的普通方程,并判断点 与曲线 的位置关系;
(2)设直线 : 与曲线 交于 、 两点,求 的值.
23、(本小题12分)
已知a,b,c为正数.
(1)求 的最小值;
(2)求证: .
参考答案
一、单选题
1、
【答 案】
B
【分析】
通过题意, ,则 .
因此正确答案为:B.
2、
【答 案】
C
【分析】
对于A选项,因为两个函数的定义域不同,所以两个函数是不同的函数,故A无误;
对于B选项,因为存在量词命题的否定是全称量词命题,所以B无误;
对于C选项,因为 ,但是 ,与增函 数定义矛盾,所以C有误;
对于D选项,若 ,当 时,推不出 ,当 时, 且 ,所以D无误.
因此正确答案为:C.
3、
【答 案】
A
【分析】
因为角 的终边在直线 上,
所以当 时,在直线上取一点 ,则 ,
当 时,在直线上取一点 ,则 ,
综上 ,
所以 ,
因此正确答案为:A.
4、
【答 案】
C
【分析】
设等差数列 的公差为 ,则通过题意可得
,解得 ,
所以 ,
因此正确答案为:C.
5、
【答 案】
D
【分析】
根据条件结构的程序框图,依次执行,即得解
【详解】
由题意,输入 , ,
第一步,判定 是否成立,由于
因此赋值 ,
第二步,判定 是否成立,由于
因此赋值
输出
故选:D
6、
【答 案】
B
【分析】
2 3
先排 , 两道程序有A3种放法,再排剩余的3道程序有A3种放法,再由分步计数原理即可得出答案.
【详解】
2
先排 , 两道程序,其既不能放在最前,也不能放在最后,则在第2,3,4道程序选两个放 , ,共有A3种放法;
3
再排剩余的3道程序,共有A3种放法;
2
则共有A3 A
3
3=36种放法.
B. 故选:
7、
【答 案】
C
【分析】
由题意得: ,
设 , ,则 ,
解得: ,
则线段 的中点横坐标为 ,
故线段 的中点到 轴的距离为 .
故选C.
8、
【答 案】
B
【分析】
根据题意可推出 即 ,可得函数 是奇函数,利用赋值法求得
以及 ,继而根据 推得函数的周期,由此利用周期求得 的值.
【详解】
因为对任 意实数x都有函数满足 ,即 ,即 ,
所以函数 是奇函数,
对于 , 令 ,则可得 ;
由 ,令 得, ,
即 ,
所以 ,即 ,
所以 ,即 12为函数 的周期,
所以 ,
故选:B.
9、
【答 案】
D
【分析】
将函数 用三角恒等变换化简成正弦型函数,根据整体代换与正弦函数的性质,结合已知建立 的不等量关
系,即可求解.
【详解】
,
在区间 上是增函数,
π π π
, , π .
当 Z Z 时, 取得最大值,
而 在区间 上恰好取得一次最大值,
,解得 ,
综上, .
故选:D.
10、
【答案 】
B
【分析】
根据全概率概率公式及条件概率概率公式计算可得;
【详解】
依题意 , , , ,故③正确;
所以 ,
所以 ,故①错误;
因为 ,所以 ,故②正确;
所以 ,故④正确;
故选:B
11、
【答 案】
A
【分析】
联立直线方程与双曲线的渐近线的方程可得 , ,进而可得 中点
,由 ,可得 ,进而可得 ,代入得 ,
,即可得答案.
【详解】
解:因为双曲线的渐近线方程为 ,
由 ,解得 ,
不妨设 ,
同理可得 ,
则 中点 ,
又因为点 满足 ,
所以点 ,
所以 ,
又因为 ,
所以 ,
所以 ,
所以 ,
所以 .
故选:A.
12、
【答 案】
C
【分析】
\lna \lna
讨论 的取值范围,利用函数图象,结合导数求出 ,构造函数 ,利用导数
求出函数的最值,进而得解.
【详解】
设 , ,
若 ,对任意 恒 成立,则 ,对任意 恒成立,
当 时,在同一坐标系中作出函数 的图象,
显然,由图可知 ,对任意 不恒成立;
当 时,在同一坐标系中作出函数 的图象 ,
由图可知,临界条件是直线 与曲线 的图象相切时,
由 ,求导 ,
设 ,解得 ,且 ,
∴当 的切线斜率为1时,切点坐标为 ,
故 ,所以
即 \lna \lna
\lna \lna
两边同除以 , ,令
\lna \lna \lna
求导
令 ,得\lna ,即
当 , ,函数 单调递增,当 , ,函数 单调递减,
\lne
所以当 ,函数 取到最大值,且
故 的最大值为
故选:C.
【点睛】
思路点睛 :本题考查不等式恒成立求参数取值范围问题,需要结合图象分类讨论,构造函数将问题转化,考查
数形结合思想、分类讨论思想、转化与化归思想和运算求解能力,是难题.
二、填空题
13、
【答案 】
【分析】
【详解】
试题分析 :由复数的运算可知 , 是纯虚数,则其实部必为零,即
,所以 .
考点:复数的运算.
14、
【答 案】
9
【分析】
,
展开式中 的系数为 C C C .
因此正确答案为:9
15、
【答 案】
【分析】
利用向量共线表示 ,以及 ,转化求得 ,
根据图形可知 ,再逐步变形转化为面积比值,即可求解.
【详解】
如图,连 结 并延长交 于点 ,
设点 到 的距离为 ,点 到 的 距离为 ,
因为 ,所以设 ,
设 , ,
所以
,
所以 ,即 ,
,
所以 .
故答案为:
16、
【答 案】
/
【分析】
设圆心为 ,由圆的性质可知, , , , , 共线, , , , , 共线,
由菱形性质可知, ,
不妨令 , ,且 半径为10,
则 = ,即 , ,
故 ,
不妨令 , ,
则 ,
从而 ; ,
故 在 上单调递增,在 上单调递减,
所以当 时, 在 上取最大值,
从而要使镂空的菱形 面积最大,则 ,
由 可知, ,
则此时 .
因此正确答案为: .
三、解答题
17、
【答 案】
(1) ; (2) .
【分析】
(1)因为 ,
由正弦定理可得 ,
又 ,
所以 ,
因为 ,则 ,所以 ,
因为 ,所以 .
(2)因为 , ,
由余弦定理可得 ,整理得 ,
又 ,解得 ,
所以 .
18、
【答 案】
(1)列联表见解析,有 的把握认为对冰壶运动是否有兴趣与性别有关.
(2)分布列见解析, .
【分析】
(1)根据题干所给数据求出冰壶运动有兴趣的男女人数,即可得到列联表,再计算出卡方,即可判断;
(2)首先利用分层抽样求出男、女抽取的人数,依题意 的所有可能取值为 , , ,求出所对应的概率 ,即
可得到分布列与数学期望;
【详解】
(1)解:依题意对冰壶运动有兴趣的人数为 人,
则女生中对冰壶运动有兴趣的有 人,
男生中对冰壶运动有兴趣的有 人,
所以男生中对冰壶运动无兴趣的有 人 ,
所以 列联表:
有兴趣 没有兴趣 合计
男
女
合计
,
有 的把握认为对冰壶运动是否有兴趣与性别有关.
(2)解:从对冰壶运动有兴趣的学生中抽取 人,抽到的男生人数、女生人数分别为: (人 ,
(人 ,
则 的所有可能取值为 , , ,
C
所以 ,
C
C C
,
C
C
,
C
故 的分布列是:
0 1 2
故 .
19、
【答 案】
(1)
(2)当n为偶数时, 取得最小值为-242;当n为奇数时, 取最小值为-243
【分析】
(1)根据题干条件得到 ,与 相减后得到 ,
故得到a1,a3,a5,…是以 为首项,2为公差的等差数列,a2,a4,a6,…是以 为首项,2为
公差的等差数列,进而求出通项公式;(2)分n为偶数和n为奇数两种情况表达出 ,并求出最小值.
【详解】
(1)∵ (n∈N*),①
②
②-①得, .
又∵a2+a1=2-44,a =- 1 23,
∴a2=-19
,
同理得,a3=-21,a4=-17.
故a1,a3,a5,…
是以 为首项,2为公差的等差数列,a2,a4,a6,…是以 为首项,2为公差
的等差数列.
从而
(2)当n为偶数时,
故当n=22时,Sn取得最小值为-242.
当n 为奇数时,
.
故当n=21或n=23时,Sn取得最小值-243.
综上所述:当n为偶数时,S n取得最小值为-242;当n为奇数时,Sn取最小值为-243.
20、
【答案 】
(1) ;(2)(ⅰ)证明见解析;(ⅱ)是,理由见解析.
【分析】
(1)通过题意得 ,
所以 ,
所以椭圆C的方程为 .
(2)(ⅰ)证明:设 ,
因为 在椭圆 上,所以 .
因为直线 的斜率为 ,直线 的斜率为 ,
所以直线 的方程为 .
所以 点的坐标为 .
所以直线 的斜率为 .
所以直线 的斜率之积为:
.
(ⅱ) 三点共线.
设直线 斜率为 ,易得 .
由(ⅰ)可知直线 斜率为 ,所以直线 的方程为 .
联立 可得 .
解得 点的纵坐标为 ,
所以 点的坐标为 .
所以,直线 的斜率为 ,直线 的斜率为 .
因为直线 的斜率等于直线 的斜率,
所以 三点共线.
21、
【答案 】
(1)
(2)
【分析】
(1)通过题意 e ,利用分离参数法得到 e 对
恒成立.设 e ,利用导数判断出函数 在 上单调递增,求出 ;
(2)把题意转化为 , 恒成立.由 为 的一个极小值点,解得 .代入原函
数验证成立.
(1)
通过 题意知 e
因为函数 在 上单调递增,所以 e ,
即 e 对 恒成立
设 e ,则 e
当 时, e
当 时, e e
所以函数 e 在 上单调递增
所以
(2)
通过 题意分析可以得 e
所以 e ,
因为 ,所以 ,
即 为 的最小值, 为 的一个极小值 点,
所以 e ,解得
当 时, e
所以 e e
①当 时, (当且仅当 时等号成立)
所以 在 上单调递增
②当 时,若 , ;
若 , g^'\left(x\right)< \text{e}^{-\frac\pi2}+\sqrt2-3+\frac2{\pi+2}< \frac12+\frac32-3+\frac2{\pi+2}< 0
所以 在 上单调递减
综上所述 在 上单调 递减,在 上单调递增
所以当 时,
【点睛】
导数是研 究函数的单调性、极值(最值)最有效的工具,而函数是高中数学中重要的知识点,对导数的应用的考
查主要从以下几个角度进行:
(1)考查导数的几何意义,往 往与解析几何、微积分相联系.
(2)利用导数求函数的单调区间,判断单调性;已知单调性,求 参数.
(3)利用导数求函数的最值(极值),解决生活中的优化问题.
(4)考查数形结合思想的应用.
22、
【答案 】
(1) , 在曲线 内部
(2)
【分析】
(1)利用消参法可得曲线 的普通方程,求得点P的直角坐标,代入曲线 的普通方程中,可判断点 与曲线
的位置关系;
(2)求出直线 的参数方程,并代入曲线方程中,得根与系数的关系式,利用参数的几何意义,求得答案.
(1)
cos
由 sin ,消参得曲线 的普通方程为: ,
cos
由 sin ,可得点P的直角坐标为 ,
将 代入曲线 的普通方程的左边得: ,故 在曲线 内部.
(2)
因为直线 : 的极坐标方程对应的普通方程为: ,
所以 在直线 上,所以可设直线 的参数方程为: (t为参数),
将其代入曲线 的普通方程 并化简整理得: , ,
设它的两根为 ,则 ,
所以: .
23、
【答案 】
(1)
(2)证 明见解析
【分析】
(1) = ,然后利用均值不等式可得答案;
(2)由 , , 可证明.
【详解】
(1)因为 = ,当且仅当“ ”时等号成立,
所以当 时, 的最小值为 .
(2)因为 ,同理 , ,
所以三式相加得 ,
所以 ,当且仅当“ ”时等号成立
量检测)
一、单选题(本大题共12小题,每小题5分,共60分)
1、已知集合 , ,那么 等于( )
A.
B.
C.
D.
2、下列命题中,错误的命题有( )
A.函数 与 不是同一个函数
B.命题“ , ”的否定为“ , ”
C.设函数 ,则 在 上单调递增
D.设 ,则 “ ”是“ ”的必要不充分条件
3、已知角 的终边在直线 上,则 ( )
A.
B.
C.1
D.
4、在等差数列 中, , ,则 ( )
A.19
B.18
C.17
D.20
5、如图所示的程序框图,输入3个数, , , ,则输出的 为( )
A.0
B.
C.
D.
6、源于探索外太空的渴望,航天事业在21世纪获得了长足的发展.太空中的环境为某些科学实验提供了有利条
件,宇航员常常在太空旅行中进行科学实验.在某次太空旅行中,宇航员们负责的科学实验要经过5道程序,其
中 , 两道程序既不能放在最前,也不能放在最后,则该实验不同程序的顺序安排共有( )
A.18种
B.36种
C.72种
D.108种
7、过抛物线 的焦点 的直线交抛物线于 、 两点,且 ,则线段 的中点到 轴的距离为(
).
A.
B.
C.
D.
8、已知函数 对任意实数x都有 且 ,则 等于
( )
A.
B.0
C.3
D.6
9、已知函数 在区间 上是增函数,且在区间
上恰好取得一次最大值,则 的取值范围是( )
A.
B.
C.
D.
10、某车间加工同一型号零件,第一 二台车床加工的零件分别占总数的40%,60%,各自产品中的次品率分别
为6%,5%.记“任取一个零件为第i台车床加工 ”为事件 ,“任取一个零件是次品”为事件B,则( )
① ② ③ ④
A.①②④
B.②③④
C.②③
D.①②③④
11、设直线 与双曲线 的两条渐近线分别交于点A,B,若点
满足 ,则该双曲线的离心率是( )
A.
B.
C.
D.
12、已知关于 的不等式 对任意 恒成立,则 的最大值为( )
A.
B.1
C.
D.
二、填空题(本大题共4小题,每小题5分,共20分)
13、 是虚数单位,若复数 是纯虚数,则实数 的值为 .
14、 的展开式中 的系数为 .
15、已知 是 内部(不含边界)一点,若 , ,则
.
16、剪纸是一种镂空艺术,是中国汉族最古老的民间艺术之一.如图,一圆形纸片,直径 cm,需要剪去
菱形 ,可以经过两次对折、沿 裁剪、展开后得到.若 ,要使镂空的菱形 面积最大,
则菱形的边长 cm.
三、解答题(本大题共7小题,共70分)
17、(本小题8分)
在 中,角A,B,C的对边分别为a,b,c,且 .
(1)求B的大小;
(2)若 ,求 的面积.
18、(本小题8分)
2022年北京冬奥会即第24届冬季奥林匹克运动会在2022年2月4日至2月20日在北京和张家口举行.某研究机构为
了解大学生对冰壶运动是否有兴趣,从某大学随机抽取男生、女生各200人,对冰壶运动有兴趣的人数占总数的
,女生中有80人对冰壶运动没有兴趣.
有兴趣没有兴趣合计
男
女 80
合计
(1)完成上面2×2列联表,并判断是否有99%的把握认为对冰壶运动是否有兴趣与性别有关?
(2)按性别用分层抽样的方法从对冰壶运动有兴趣的学生中抽取9人,若从这9人中随机选出2 人作为冰壶运动的
宣传员,设X表示选出的2人中女生的人数,求X的分布列和数学期望.
附: .
0.100 0.050 0.025 0.010 0.001
2.706 3.841 5.024 6.635 10.828
19、(本小题8分)
在数列{an}中, (n∈N*), .
(1) 求 ;
(2)设 为 的前n项和,求 的最小值.
20、(本小题10分)
已知椭圆 长轴的两个端点分别为 ,离心率为 .
(1)求椭圆 的方程;
(2) 为椭圆 上异于 的动点,直线 分别交直线 于 两点,连接 并延长交椭圆 于
点 .
(ⅰ)求 证:直线 的斜率之积为定值;
(ⅱ)判断 三点是否共线,并说明理由 .
21、(本小题12分)
已知函数 e .
(1)若函数 在 上单调递增,求实 数 的取值范围;
(2)设函数 ,若 ,求 的值.
22、(本小题12分)
在平面直角坐标系 中,曲线 的参数方程为: ( 为参数),在以 为极点, 轴的非
负半轴为极轴的极坐标系中,点 的极坐标为 .
(1)写出曲线 的普通方程,并判断点 与曲线 的位置关系;
(2)设直线 : 与曲线 交于 、 两点,求 的值.
23、(本小题12分)
已知a,b,c为正数.
(1)求 的最小值;
(2)求证: .
参考答案
一、单选题
1、
【答 案】
B
【分析】
通过题意, ,则 .
因此正确答案为:B.
2、
【答 案】
C
【分析】
对于A选项,因为两个函数的定义域不同,所以两个函数是不同的函数,故A无误;
对于B选项,因为存在量词命题的否定是全称量词命题,所以B无误;
对于C选项,因为 ,但是 ,与增函 数定义矛盾,所以C有误;
对于D选项,若 ,当 时,推不出 ,当 时, 且 ,所以D无误.
因此正确答案为:C.
3、
【答 案】
A
【分析】
因为角 的终边在直线 上,
所以当 时,在直线上取一点 ,则 ,
当 时,在直线上取一点 ,则 ,
综上 ,
所以 ,
因此正确答案为:A.
4、
【答 案】
C
【分析】
设等差数列 的公差为 ,则通过题意可得
,解得 ,
所以 ,
因此正确答案为:C.
5、
【答 案】
D
【分析】
根据条件结构的程序框图,依次执行,即得解
【详解】
由题意,输入 , ,
第一步,判定 是否成立,由于
因此赋值 ,
第二步,判定 是否成立,由于
因此赋值
输出
故选:D
6、
【答 案】
B
【分析】
2 3
先排 , 两道程序有A3种放法,再排剩余的3道程序有A3种放法,再由分步计数原理即可得出答案.
【详解】
2
先排 , 两道程序,其既不能放在最前,也不能放在最后,则在第2,3,4道程序选两个放 , ,共有A3种放法;
3
再排剩余的3道程序,共有A3种放法;
2
则共有A3 A
3
3=36种放法.
B. 故选:
7、
【答 案】
C
【分析】
由题意得: ,
设 , ,则 ,
解得: ,
则线段 的中点横坐标为 ,
故线段 的中点到 轴的距离为 .
故选C.
8、
【答 案】
B
【分析】
根据题意可推出 即 ,可得函数 是奇函数,利用赋值法求得
以及 ,继而根据 推得函数的周期,由此利用周期求得 的值.
【详解】
因为对任 意实数x都有函数满足 ,即 ,即 ,
所以函数 是奇函数,
对于 , 令 ,则可得 ;
由 ,令 得, ,
即 ,
所以 ,即 ,
所以 ,即 12为函数 的周期,
所以 ,
故选:B.
9、
【答 案】
D
【分析】
将函数 用三角恒等变换化简成正弦型函数,根据整体代换与正弦函数的性质,结合已知建立 的不等量关
系,即可求解.
【详解】
,
在区间 上是增函数,
π π π
, , π .
当 Z Z 时, 取得最大值,
而 在区间 上恰好取得一次最大值,
,解得 ,
综上, .
故选:D.
10、
【答案 】
B
【分析】
根据全概率概率公式及条件概率概率公式计算可得;
【详解】
依题意 , , , ,故③正确;
所以 ,
所以 ,故①错误;
因为 ,所以 ,故②正确;
所以 ,故④正确;
故选:B
11、
【答 案】
A
【分析】
联立直线方程与双曲线的渐近线的方程可得 , ,进而可得 中点
,由 ,可得 ,进而可得 ,代入得 ,
,即可得答案.
【详解】
解:因为双曲线的渐近线方程为 ,
由 ,解得 ,
不妨设 ,
同理可得 ,
则 中点 ,
又因为点 满足 ,
所以点 ,
所以 ,
又因为 ,
所以 ,
所以 ,
所以 ,
所以 .
故选:A.
12、
【答 案】
C
【分析】
\lna \lna
讨论 的取值范围,利用函数图象,结合导数求出 ,构造函数 ,利用导数
求出函数的最值,进而得解.
【详解】
设 , ,
若 ,对任意 恒 成立,则 ,对任意 恒成立,
当 时,在同一坐标系中作出函数 的图象,
显然,由图可知 ,对任意 不恒成立;
当 时,在同一坐标系中作出函数 的图象 ,
由图可知,临界条件是直线 与曲线 的图象相切时,
由 ,求导 ,
设 ,解得 ,且 ,
∴当 的切线斜率为1时,切点坐标为 ,
故 ,所以
即 \lna \lna
\lna \lna
两边同除以 , ,令
\lna \lna \lna
求导
令 ,得\lna ,即
当 , ,函数 单调递增,当 , ,函数 单调递减,
\lne
所以当 ,函数 取到最大值,且
故 的最大值为
故选:C.
【点睛】
思路点睛 :本题考查不等式恒成立求参数取值范围问题,需要结合图象分类讨论,构造函数将问题转化,考查
数形结合思想、分类讨论思想、转化与化归思想和运算求解能力,是难题.
二、填空题
13、
【答案 】
【分析】
【详解】
试题分析 :由复数的运算可知 , 是纯虚数,则其实部必为零,即
,所以 .
考点:复数的运算.
14、
【答 案】
9
【分析】
,
展开式中 的系数为 C C C .
因此正确答案为:9
15、
【答 案】
【分析】
利用向量共线表示 ,以及 ,转化求得 ,
根据图形可知 ,再逐步变形转化为面积比值,即可求解.
【详解】
如图,连 结 并延长交 于点 ,
设点 到 的距离为 ,点 到 的 距离为 ,
因为 ,所以设 ,
设 , ,
所以
,
所以 ,即 ,
,
所以 .
故答案为:
16、
【答 案】
/
【分析】
设圆心为 ,由圆的性质可知, , , , , 共线, , , , , 共线,
由菱形性质可知, ,
不妨令 , ,且 半径为10,
则 = ,即 , ,
故 ,
不妨令 , ,
则 ,
从而 ; ,
故 在 上单调递增,在 上单调递减,
所以当 时, 在 上取最大值,
从而要使镂空的菱形 面积最大,则 ,
由 可知, ,
则此时 .
因此正确答案为: .
三、解答题
17、
【答 案】
(1) ; (2) .
【分析】
(1)因为 ,
由正弦定理可得 ,
又 ,
所以 ,
因为 ,则 ,所以 ,
因为 ,所以 .
(2)因为 , ,
由余弦定理可得 ,整理得 ,
又 ,解得 ,
所以 .
18、
【答 案】
(1)列联表见解析,有 的把握认为对冰壶运动是否有兴趣与性别有关.
(2)分布列见解析, .
【分析】
(1)根据题干所给数据求出冰壶运动有兴趣的男女人数,即可得到列联表,再计算出卡方,即可判断;
(2)首先利用分层抽样求出男、女抽取的人数,依题意 的所有可能取值为 , , ,求出所对应的概率 ,即
可得到分布列与数学期望;
【详解】
(1)解:依题意对冰壶运动有兴趣的人数为 人,
则女生中对冰壶运动有兴趣的有 人,
男生中对冰壶运动有兴趣的有 人,
所以男生中对冰壶运动无兴趣的有 人 ,
所以 列联表:
有兴趣 没有兴趣 合计
男
女
合计
,
有 的把握认为对冰壶运动是否有兴趣与性别有关.
(2)解:从对冰壶运动有兴趣的学生中抽取 人,抽到的男生人数、女生人数分别为: (人 ,
(人 ,
则 的所有可能取值为 , , ,
C
所以 ,
C
C C
,
C
C
,
C
故 的分布列是:
0 1 2
故 .
19、
【答 案】
(1)
(2)当n为偶数时, 取得最小值为-242;当n为奇数时, 取最小值为-243
【分析】
(1)根据题干条件得到 ,与 相减后得到 ,
故得到a1,a3,a5,…是以 为首项,2为公差的等差数列,a2,a4,a6,…是以 为首项,2为
公差的等差数列,进而求出通项公式;(2)分n为偶数和n为奇数两种情况表达出 ,并求出最小值.
【详解】
(1)∵ (n∈N*),①
②
②-①得, .
又∵a2+a1=2-44,a =- 1 23,
∴a2=-19
,
同理得,a3=-21,a4=-17.
故a1,a3,a5,…
是以 为首项,2为公差的等差数列,a2,a4,a6,…是以 为首项,2为公差
的等差数列.
从而
(2)当n为偶数时,
故当n=22时,Sn取得最小值为-242.
当n 为奇数时,
.
故当n=21或n=23时,Sn取得最小值-243.
综上所述:当n为偶数时,S n取得最小值为-242;当n为奇数时,Sn取最小值为-243.
20、
【答案 】
(1) ;(2)(ⅰ)证明见解析;(ⅱ)是,理由见解析.
【分析】
(1)通过题意得 ,
所以 ,
所以椭圆C的方程为 .
(2)(ⅰ)证明:设 ,
因为 在椭圆 上,所以 .
因为直线 的斜率为 ,直线 的斜率为 ,
所以直线 的方程为 .
所以 点的坐标为 .
所以直线 的斜率为 .
所以直线 的斜率之积为:
.
(ⅱ) 三点共线.
设直线 斜率为 ,易得 .
由(ⅰ)可知直线 斜率为 ,所以直线 的方程为 .
联立 可得 .
解得 点的纵坐标为 ,
所以 点的坐标为 .
所以,直线 的斜率为 ,直线 的斜率为 .
因为直线 的斜率等于直线 的斜率,
所以 三点共线.
21、
【答案 】
(1)
(2)
【分析】
(1)通过题意 e ,利用分离参数法得到 e 对
恒成立.设 e ,利用导数判断出函数 在 上单调递增,求出 ;
(2)把题意转化为 , 恒成立.由 为 的一个极小值点,解得 .代入原函
数验证成立.
(1)
通过 题意知 e
因为函数 在 上单调递增,所以 e ,
即 e 对 恒成立
设 e ,则 e
当 时, e
当 时, e e
所以函数 e 在 上单调递增
所以
(2)
通过 题意分析可以得 e
所以 e ,
因为 ,所以 ,
即 为 的最小值, 为 的一个极小值 点,
所以 e ,解得
当 时, e
所以 e e
①当 时, (当且仅当 时等号成立)
所以 在 上单调递增
②当 时,若 , ;
若 , g^'\left(x\right)< \text{e}^{-\frac\pi2}+\sqrt2-3+\frac2{\pi+2}< \frac12+\frac32-3+\frac2{\pi+2}< 0
所以 在 上单调递减
综上所述 在 上单调 递减,在 上单调递增
所以当 时,
【点睛】
导数是研 究函数的单调性、极值(最值)最有效的工具,而函数是高中数学中重要的知识点,对导数的应用的考
查主要从以下几个角度进行:
(1)考查导数的几何意义,往 往与解析几何、微积分相联系.
(2)利用导数求函数的单调区间,判断单调性;已知单调性,求 参数.
(3)利用导数求函数的最值(极值),解决生活中的优化问题.
(4)考查数形结合思想的应用.
22、
【答案 】
(1) , 在曲线 内部
(2)
【分析】
(1)利用消参法可得曲线 的普通方程,求得点P的直角坐标,代入曲线 的普通方程中,可判断点 与曲线
的位置关系;
(2)求出直线 的参数方程,并代入曲线方程中,得根与系数的关系式,利用参数的几何意义,求得答案.
(1)
cos
由 sin ,消参得曲线 的普通方程为: ,
cos
由 sin ,可得点P的直角坐标为 ,
将 代入曲线 的普通方程的左边得: ,故 在曲线 内部.
(2)
因为直线 : 的极坐标方程对应的普通方程为: ,
所以 在直线 上,所以可设直线 的参数方程为: (t为参数),
将其代入曲线 的普通方程 并化简整理得: , ,
设它的两根为 ,则 ,
所以: .
23、
【答案 】
(1)
(2)证 明见解析
【分析】
(1) = ,然后利用均值不等式可得答案;
(2)由 , , 可证明.
【详解】
(1)因为 = ,当且仅当“ ”时等号成立,
所以当 时, 的最小值为 .
(2)因为 ,同理 , ,
所以三式相加得 ,
所以 ,当且仅当“ ”时等号成立
同课章节目录
