2022~2023学年河南郑州金水区郑州市回民中学高一上学期期中数学试卷(图片版,含解析)
文档属性
| 名称 | 2022~2023学年河南郑州金水区郑州市回民中学高一上学期期中数学试卷(图片版,含解析) |  | |
| 格式 | |||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-01 17:37:46 | ||
图片预览



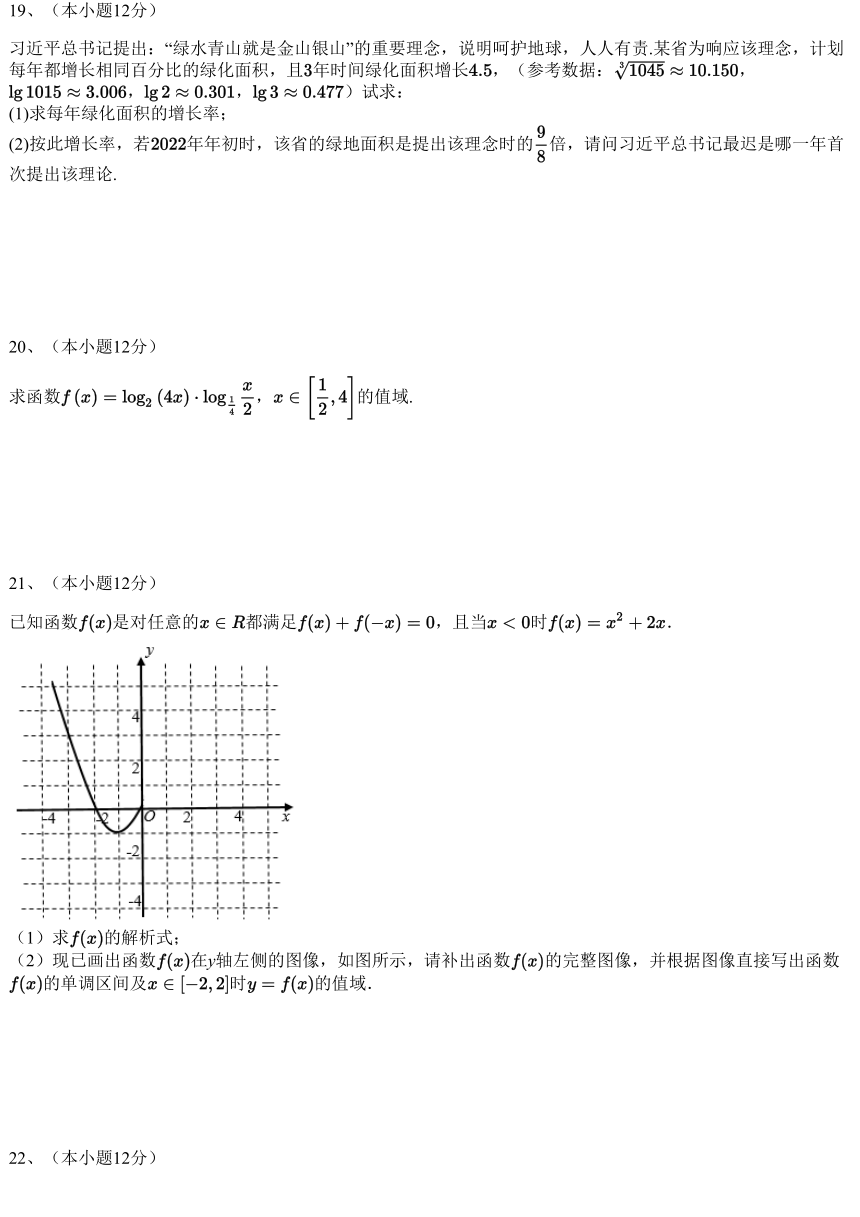

文档简介
2022~2023学年河南郑州金水区郑州市回民中学高一上学期期中数学试卷
一、单选题(本大题共8小题,每小题5分,共40分)
1、命题“ , ”的否定是( )
A. ,
B. ,
C. ,
D. ,
2、已知集合 ,则满足条件 的集合 的
个数为( )
A.1
B.2
C.3
D.4
3、函数 的定义域为( ).
A.
B.
C.
D. 且
4、设函数 ,则 的值为
A.
B.
C.
D.
5、设 , , ,则 , , 的大小关系是( ).
A.
B.
C.
D.
6、设奇函数f(x)在(0,+∞)上为减函数,且f(1)=0,则不等式 <0的解集为( )
A.(-1,0)∪(1,+∞)
B.(-∞,-1)∪(0,1)
C.(-∞,-1)∪(1,+∞)
D.(-1,0)∪(0,1)
7、若定义在R上的函数 满足:对任意 , R,有 ,则下列说法一定
正确的是( )
A. 为奇函数
B. 为偶函数
C. 为奇函数
D. 为偶函数
8、已知定义在R上的奇函数满足 ,且在区间 上单调递增,则( )
A.
B.
C.
D.
二、多选题(本大题共4小题,每小题5分,共20分)
9、设偶函数 在 上单调递增,则下列大小关系是( )
A.
B.
C.
D.
10、不等式 成立的一个充分不必要条件是( )
A.
B.
C.
D.
11、已知实数 , , 满足 , ,则( )
A.
B.
C.若 ,则
D.若 ,则
12、已知函数 ,设 , ,则( )
A.若 ,则
B.若 ,则
C.若 ,则
D.若 ,则
三、填空题(本大题共4小题,每小题5分,共20分)
13、已知 ,则 (用含a,b的式子表示).
14、设集合 或 , , ,则a的取值范围是 .
15、已知x>0,y>0,2x+3y=6,则xy的最大值为 .
16、已知函数 , ,若对于任意的 ,总存在 ,使得 或
e
,则实数 的取值范围是 .
四、解答题(本大题共6小题,共70分)
17、(本小题10分)
计算下列各式的值:
(1) ;
(2) .
18、(本小题12分)
已知 ,
(1 )若 时,求 ;
(2)若 ,求实数m的取值范围.
19、(本小题12分)
习近平总书记提出:“绿水青山就是金山银山”的重要理念,说明呵护地球,人人有责.某省为响应该理念,计划
每年都增长相同百分比的绿化面积,且 年时间绿化面积增长 ,(参考数据: ,
, , )试求:
(1)求每年绿化面积的增长率;
(2)按此增长率,若 年年初时,该省的绿地面积是提出该理念时的 倍,请问习近平总书记最迟是哪一年首
次提出该理论.
20、(本小题12分)
求函数 , 的值域.
21、(本小题12分)
已知函数 是对任意的 都满足 ,且当 时 .
(1)求 的解析式;
(2)现已画出函数 在 y轴左侧的图像,如图所示,请补出函数 的完整图像,并根据图像直接写出函数
的单调区间及 时 的值域.
22、(本小题12分)
已知函数 .
(1)判断函数 在R上的单调性,并用单调性的定义证明;
(2)判断函数 的奇偶性,并证明;
(3)若 恒成立,求实数k的取值范围.
参考答案
一、单选题
1、
【答 案】
A
【分析】
因为特称命题的否定是全称命题,
所以命题“ , ”的 否定是: , ,
因此正确答案为:A.
2、
【答 案】
D
【分析】
【详解】
求解一元二 次方程,得
,易知 .
因为 ,所以根据子集的定义,
集合 必须含有元素1,2,且可能含有元素3 ,4,
原题即求集合 的子集个数,即有 个 ,故选D.
【点评】
本题考查 子集的概念,不等式,解一元二次方程.本题在求集合个数时,也可采用列举法.列出集合 的所有可能
情况,再数个数即可.来年要注意集合的交集运算,考查频度极高.
3、
【答 案】
D
【分析】
对于函数 ,有 ,解得 且 ,
因此,函数 的定义域为 且 .
因此正确答案为:D.
4、
【答 案】
A
【分析】
因为 时,
所以 ;
又 时, ,
所以 因此正确答案为A.
本题考查分段函数的意义,函数值的运算.
5、
【答 案】
C
【分析】
由 在区间 上是单调减函数可知, ,
又 ,
故选C.
6、
【答 案】
C
【分析】
∵f(x)为奇函数,故可得 ,
则 <0等价于 .
∵f(x)在(0,+∞)上为减函数且f(1)=0,
∴当x>1时,f(x)<0.
∵奇函数图象关于原点 对称,∴在(-∞,0)上f(x)为减函数且f(-1)=0,
即x<-1时,f(x)>0.
综上使 <0的解集为(-∞,-1)∪(1,+∞).
因此正确答案为: .
7、
【答 案】
C
【分析】
对任意 , R有 ,
令 ,得 .
令 , ,得 .
整理得 ,故 为奇函数.
因此正确答案为:C
8、
【答 案】
D
【分析】
∵ ,
∴ ,同理 ,
又奇函数 在区间 上单调递增,故在区间 上 单调递增,
∴ ,即 .
因此正确答案为:D
二、多选题
9、
【答 案】
B;C
【分析】
因为函数 是偶函数,则 恒成立,所以 ,
又函数在 上单调递增,所以在 上单调递减,则 ,
所以 且 ,
所以 , .
因此正确答案为:BC
10、
【答 案】
A;B
【分析】
解:令 ,
所以,不等式 ,解得 或
所以, 或 ,解得 或 ,
所以,不等式 的解集为 ,
因为所求的是不等式 成立的一个充分不必要条件,
故只需满足是 真子集即可,
所以,只有AB选项满足,CD选项不满足.
因此正确答案为:AB
11、
【答 案】
A;C
【分析】
由于实数 , , 满足 , ,
故 ,否则 ,则 ,则 ,不合题意;
故由 ,可得 ,A无误;
取 满足 , ,
但 ,故B有误;
若 ,则 ,则 ,
即 ,C无误;
取 ,满足 且 , ,
但 ,D有误;
因此正确答案为:AC
12、
【答 案】
A;B;D
【分析】
作出函数 的图象,如图示:
当 时,由于 ,可知 ,
则 ,则 ,即 ,A无误;
由于 ,则 ,即 ,B无误;
当 时, 单调递增,当 时,有 ,
即 ,不符合C,D选项;
当 时, ,由于 ,则 ,即 ,
当 时, 递增,若 ,则 即 ,
当 时, 递减,
若 ,则 ,即 ;
若 ,则由 ,令 ,
由于此时 ,则 ,
由 ,可得 ,即 ,故C有误,D无误,
因此正确答案为:ABD
三、填空题
13、
【答 案】
【分析】
由 ,得 ,又 ,
.
因此正确答案为 .
14、
【答案 】
【分析】
由题意, ,可得 ,求解即可
【详解】
由题意, 集合 或 , ,
因为 ,故可得
解得 .
故答案为:
15、
【答 案】
【分析】
因为x>0,y>0,2x+3y=6,所以 .
当且仅当2x=3y,即 时,xy取到最大值 .
因此正确答案为: .
16、
【答 案】
【分析】
解:记函数 的值域为 , 的值域为 ,
因为对于任意的 ,总存在 ,使得 或 ,
所以, R
因为e ,e ,
所以 ,即函数 的值域为 ,
e
当 时, 时, ,当且仅当 时等号成立,
所以,根据对勾函数的性质可知, 的值域为 ,
因为 R,
所以,有 ,解得 ,
当 时, 的值域为R,满足 R,故 时成立,
综上所述,实数 的范围为 .
因此正确答案为:
四、解答题
17、
【答 案】
(1)9
(2)0
【分析】
(1)解:
(2)解:
lg lg
lg
lg lg
18、
【答案 】
(1) ;(2) .
【分析】
(1)利用集合的并集定义代入计算即可;
(2)求出集合 ,利用集合包含关系, 分类讨论 和 两种情况,列出关于m的不等式,求解可得
答案.
【详解 】
(1)当 时, ,则
即 .
(2) 或 ,由 ,可分以下两种情况:
①当 时, ,解得:
②当 时,利用数轴表示集合,如图
由图可知 或 ,解得 ;
综上所述,实数m的取值范围是: 或 ,
即
【点睛】
易错点睛: 本题考查利用集合子集关系确定参数问题,易错点是要注意: 是任何集合的子集,所以要分集合
和集合 两种情况讨论,考查学生的逻辑推理能力,属于中档题.
19、
【答案 】
(1)约为 ;
(2) 年.
【分析】
(1)解:设每年绿化面积的增长率为 ,则 ,则 ,
故每年绿化面积的增长率约为 .
(2)解:设经过 年后该省的绿地面积是提出该理念时的 倍,
则 ,则 ,而 ,
因此,习近平总书记最迟在 年首次提出该理论.
20、
【答 案】
【分析】
.
设 ,且 ,故 ,
则 且 ,图象的对称轴为 ,
∴函数 在 上单调递增,在 上单调递减,
∴当 时, ,当 时, .
∴ 的值城为 .
21、
【答案 】
(1) ;(2)图像见解析;函数 的单调减区间是 和 ,减区间
是 ;值域为 .
【分析】
解:(1) , ,设 时, ,
通过题意知 ,即 ,故 ; 时,
,故 ,
故 的解析式为 ;
(2)由 ,知 是奇函数,图像关于原点中心对称,故函数 的完整图像如下图所示:
由图像分析可得,函数 的单调减区间是 和 ,减区间是 , 时 的
值域为 .
22、
【答 案】
(1) 在R上的单调递增,证明见解析;
(2) 是奇函数,证明见解析;
(3) .
【分析】
(1)函数是增函数,任取 ,不妨设 ,
,
∵ ,
∴ ,又 ,
∴ ,即 ,
∴函数 是 上的增函数.
(2)函数为奇函数,证明如 下:
由解析式可得: ,且定义域为 关于原点对称,
,
∴函数 是定义域内的奇函数.
(3)由 等价于 ,
∵ 是 上的单调增函数,
∴ ,即 恒成立,
∴ ,解得 .
一、单选题(本大题共8小题,每小题5分,共40分)
1、命题“ , ”的否定是( )
A. ,
B. ,
C. ,
D. ,
2、已知集合 ,则满足条件 的集合 的
个数为( )
A.1
B.2
C.3
D.4
3、函数 的定义域为( ).
A.
B.
C.
D. 且
4、设函数 ,则 的值为
A.
B.
C.
D.
5、设 , , ,则 , , 的大小关系是( ).
A.
B.
C.
D.
6、设奇函数f(x)在(0,+∞)上为减函数,且f(1)=0,则不等式 <0的解集为( )
A.(-1,0)∪(1,+∞)
B.(-∞,-1)∪(0,1)
C.(-∞,-1)∪(1,+∞)
D.(-1,0)∪(0,1)
7、若定义在R上的函数 满足:对任意 , R,有 ,则下列说法一定
正确的是( )
A. 为奇函数
B. 为偶函数
C. 为奇函数
D. 为偶函数
8、已知定义在R上的奇函数满足 ,且在区间 上单调递增,则( )
A.
B.
C.
D.
二、多选题(本大题共4小题,每小题5分,共20分)
9、设偶函数 在 上单调递增,则下列大小关系是( )
A.
B.
C.
D.
10、不等式 成立的一个充分不必要条件是( )
A.
B.
C.
D.
11、已知实数 , , 满足 , ,则( )
A.
B.
C.若 ,则
D.若 ,则
12、已知函数 ,设 , ,则( )
A.若 ,则
B.若 ,则
C.若 ,则
D.若 ,则
三、填空题(本大题共4小题,每小题5分,共20分)
13、已知 ,则 (用含a,b的式子表示).
14、设集合 或 , , ,则a的取值范围是 .
15、已知x>0,y>0,2x+3y=6,则xy的最大值为 .
16、已知函数 , ,若对于任意的 ,总存在 ,使得 或
e
,则实数 的取值范围是 .
四、解答题(本大题共6小题,共70分)
17、(本小题10分)
计算下列各式的值:
(1) ;
(2) .
18、(本小题12分)
已知 ,
(1 )若 时,求 ;
(2)若 ,求实数m的取值范围.
19、(本小题12分)
习近平总书记提出:“绿水青山就是金山银山”的重要理念,说明呵护地球,人人有责.某省为响应该理念,计划
每年都增长相同百分比的绿化面积,且 年时间绿化面积增长 ,(参考数据: ,
, , )试求:
(1)求每年绿化面积的增长率;
(2)按此增长率,若 年年初时,该省的绿地面积是提出该理念时的 倍,请问习近平总书记最迟是哪一年首
次提出该理论.
20、(本小题12分)
求函数 , 的值域.
21、(本小题12分)
已知函数 是对任意的 都满足 ,且当 时 .
(1)求 的解析式;
(2)现已画出函数 在 y轴左侧的图像,如图所示,请补出函数 的完整图像,并根据图像直接写出函数
的单调区间及 时 的值域.
22、(本小题12分)
已知函数 .
(1)判断函数 在R上的单调性,并用单调性的定义证明;
(2)判断函数 的奇偶性,并证明;
(3)若 恒成立,求实数k的取值范围.
参考答案
一、单选题
1、
【答 案】
A
【分析】
因为特称命题的否定是全称命题,
所以命题“ , ”的 否定是: , ,
因此正确答案为:A.
2、
【答 案】
D
【分析】
【详解】
求解一元二 次方程,得
,易知 .
因为 ,所以根据子集的定义,
集合 必须含有元素1,2,且可能含有元素3 ,4,
原题即求集合 的子集个数,即有 个 ,故选D.
【点评】
本题考查 子集的概念,不等式,解一元二次方程.本题在求集合个数时,也可采用列举法.列出集合 的所有可能
情况,再数个数即可.来年要注意集合的交集运算,考查频度极高.
3、
【答 案】
D
【分析】
对于函数 ,有 ,解得 且 ,
因此,函数 的定义域为 且 .
因此正确答案为:D.
4、
【答 案】
A
【分析】
因为 时,
所以 ;
又 时, ,
所以 因此正确答案为A.
本题考查分段函数的意义,函数值的运算.
5、
【答 案】
C
【分析】
由 在区间 上是单调减函数可知, ,
又 ,
故选C.
6、
【答 案】
C
【分析】
∵f(x)为奇函数,故可得 ,
则 <0等价于 .
∵f(x)在(0,+∞)上为减函数且f(1)=0,
∴当x>1时,f(x)<0.
∵奇函数图象关于原点 对称,∴在(-∞,0)上f(x)为减函数且f(-1)=0,
即x<-1时,f(x)>0.
综上使 <0的解集为(-∞,-1)∪(1,+∞).
因此正确答案为: .
7、
【答 案】
C
【分析】
对任意 , R有 ,
令 ,得 .
令 , ,得 .
整理得 ,故 为奇函数.
因此正确答案为:C
8、
【答 案】
D
【分析】
∵ ,
∴ ,同理 ,
又奇函数 在区间 上单调递增,故在区间 上 单调递增,
∴ ,即 .
因此正确答案为:D
二、多选题
9、
【答 案】
B;C
【分析】
因为函数 是偶函数,则 恒成立,所以 ,
又函数在 上单调递增,所以在 上单调递减,则 ,
所以 且 ,
所以 , .
因此正确答案为:BC
10、
【答 案】
A;B
【分析】
解:令 ,
所以,不等式 ,解得 或
所以, 或 ,解得 或 ,
所以,不等式 的解集为 ,
因为所求的是不等式 成立的一个充分不必要条件,
故只需满足是 真子集即可,
所以,只有AB选项满足,CD选项不满足.
因此正确答案为:AB
11、
【答 案】
A;C
【分析】
由于实数 , , 满足 , ,
故 ,否则 ,则 ,则 ,不合题意;
故由 ,可得 ,A无误;
取 满足 , ,
但 ,故B有误;
若 ,则 ,则 ,
即 ,C无误;
取 ,满足 且 , ,
但 ,D有误;
因此正确答案为:AC
12、
【答 案】
A;B;D
【分析】
作出函数 的图象,如图示:
当 时,由于 ,可知 ,
则 ,则 ,即 ,A无误;
由于 ,则 ,即 ,B无误;
当 时, 单调递增,当 时,有 ,
即 ,不符合C,D选项;
当 时, ,由于 ,则 ,即 ,
当 时, 递增,若 ,则 即 ,
当 时, 递减,
若 ,则 ,即 ;
若 ,则由 ,令 ,
由于此时 ,则 ,
由 ,可得 ,即 ,故C有误,D无误,
因此正确答案为:ABD
三、填空题
13、
【答 案】
【分析】
由 ,得 ,又 ,
.
因此正确答案为 .
14、
【答案 】
【分析】
由题意, ,可得 ,求解即可
【详解】
由题意, 集合 或 , ,
因为 ,故可得
解得 .
故答案为:
15、
【答 案】
【分析】
因为x>0,y>0,2x+3y=6,所以 .
当且仅当2x=3y,即 时,xy取到最大值 .
因此正确答案为: .
16、
【答 案】
【分析】
解:记函数 的值域为 , 的值域为 ,
因为对于任意的 ,总存在 ,使得 或 ,
所以, R
因为e ,e ,
所以 ,即函数 的值域为 ,
e
当 时, 时, ,当且仅当 时等号成立,
所以,根据对勾函数的性质可知, 的值域为 ,
因为 R,
所以,有 ,解得 ,
当 时, 的值域为R,满足 R,故 时成立,
综上所述,实数 的范围为 .
因此正确答案为:
四、解答题
17、
【答 案】
(1)9
(2)0
【分析】
(1)解:
(2)解:
lg lg
lg
lg lg
18、
【答案 】
(1) ;(2) .
【分析】
(1)利用集合的并集定义代入计算即可;
(2)求出集合 ,利用集合包含关系, 分类讨论 和 两种情况,列出关于m的不等式,求解可得
答案.
【详解 】
(1)当 时, ,则
即 .
(2) 或 ,由 ,可分以下两种情况:
①当 时, ,解得:
②当 时,利用数轴表示集合,如图
由图可知 或 ,解得 ;
综上所述,实数m的取值范围是: 或 ,
即
【点睛】
易错点睛: 本题考查利用集合子集关系确定参数问题,易错点是要注意: 是任何集合的子集,所以要分集合
和集合 两种情况讨论,考查学生的逻辑推理能力,属于中档题.
19、
【答案 】
(1)约为 ;
(2) 年.
【分析】
(1)解:设每年绿化面积的增长率为 ,则 ,则 ,
故每年绿化面积的增长率约为 .
(2)解:设经过 年后该省的绿地面积是提出该理念时的 倍,
则 ,则 ,而 ,
因此,习近平总书记最迟在 年首次提出该理论.
20、
【答 案】
【分析】
.
设 ,且 ,故 ,
则 且 ,图象的对称轴为 ,
∴函数 在 上单调递增,在 上单调递减,
∴当 时, ,当 时, .
∴ 的值城为 .
21、
【答案 】
(1) ;(2)图像见解析;函数 的单调减区间是 和 ,减区间
是 ;值域为 .
【分析】
解:(1) , ,设 时, ,
通过题意知 ,即 ,故 ; 时,
,故 ,
故 的解析式为 ;
(2)由 ,知 是奇函数,图像关于原点中心对称,故函数 的完整图像如下图所示:
由图像分析可得,函数 的单调减区间是 和 ,减区间是 , 时 的
值域为 .
22、
【答 案】
(1) 在R上的单调递增,证明见解析;
(2) 是奇函数,证明见解析;
(3) .
【分析】
(1)函数是增函数,任取 ,不妨设 ,
,
∵ ,
∴ ,又 ,
∴ ,即 ,
∴函数 是 上的增函数.
(2)函数为奇函数,证明如 下:
由解析式可得: ,且定义域为 关于原点对称,
,
∴函数 是定义域内的奇函数.
(3)由 等价于 ,
∵ 是 上的单调增函数,
∴ ,即 恒成立,
∴ ,解得 .
同课章节目录
