2022~2023学年江苏镇江扬中市扬中市第二高级中学高一下学期期中数学试卷(图片版,含解析)
文档属性
| 名称 | 2022~2023学年江苏镇江扬中市扬中市第二高级中学高一下学期期中数学试卷(图片版,含解析) |  | |
| 格式 | |||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-02 09:51:23 | ||
图片预览



文档简介
2022~2023学年江苏镇江扬中市扬中市第二高级中学高一下学期期中数学
试卷
一、单选题(本大题共8小题,每小题5分,共40分)
1、在复平面内,复数 i对应的点所在的象限是( )
A.第一象限
B.第二象限
C.第三象限
D.第四象限
2、已知 则 ( )
A.
B.
C.
D.
3、已知 且 都是第二象限角,则 ( )
A.
B.
C.
D.
4、设 是平面内的一组基底, ,则( )
A. 三点共线
B. 三点共线
C. 三点共线
D. 三点共线
5、函数 的最小正周期是( )
A.
B.
C.
D.
6、在 中,已知 ,则 的形状是( )
A.等腰三角形
B.直角三角形
C.等边三角形
D.等腰或直角三角形
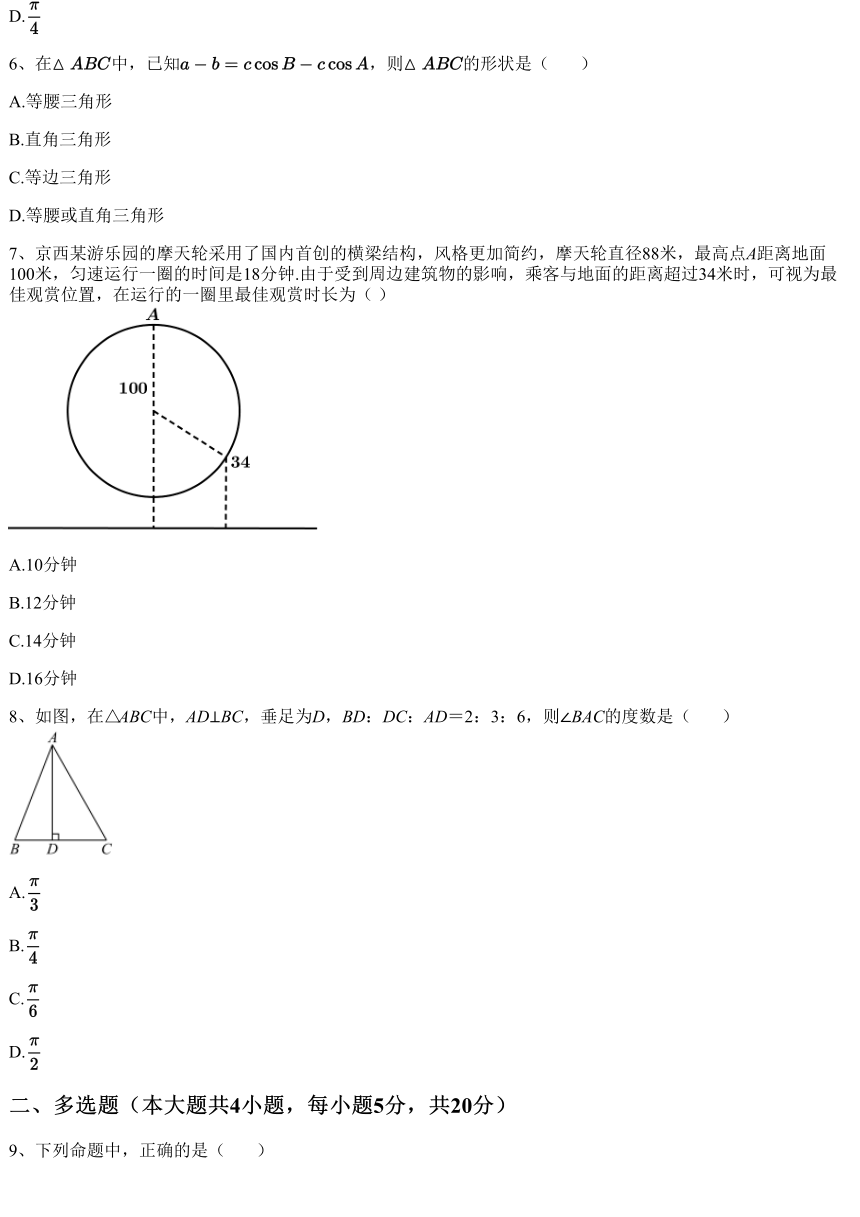
7、京西某游乐园的摩天轮采用了国内首创的横梁结构,风格更加简约,摩天轮直径88米,最高点A距离地面
100米,匀速运行一圈的时间是18分钟.由于受到周边建筑物的影响,乘客与地面的距离超过34米时,可视为最
佳观赏位置,在运行的一圈里最佳观赏时长为( )
A.10分钟
B.12分钟
C.14分钟
D.16分钟
8、如图,在△ABC中,AD⊥BC,垂足为D,BD:DC:AD=2:3:6,则∠BAC的度数是( )
A.
B.
C.
D.
二、多选题(本大题共4小题,每小题5分,共20分)
9、下列命题中,正确的是( )
A.若 ,则
B.若 ,则
C.若 ,则
D.若 ,则
10、下列化简正确的是( )
A.
B.
C.
D.
11、已知i为虚数单位,复数 i, i,且 ,则实数 的值可为( )
A.
B.
C.
D.
12、如图,设Ox,Oy是平面内相交成60°角的两条数轴, , 分别是与x轴 y轴正方向同向的单位向量.若向量
,则把有序数对 叫做向量 在坐标系xOy中的坐标.若在坐标系xOy中 ,
,则下列结论正确的是( )
A.
B.
C.
D. 与 的夹角为
3
三、填空题(本大题共4小题,每小题5分,共20分)
13、已知i为虚数单位,复数z满足 ,那么 的最小值是 .
14、已知 ,则 .
15、如图,点 , 是线段 的三等分点,以 , 为基底表示 .
16、已知向量 满足 ,且 与 的夹角为 , 与 的夹角为 , 则 .
四、解答题(本大题共6小题,共70分)
17、(本小题10分)
在复平面内,复数 i(其中i为虚数单位, R).
(1)若复数z为纯虚数,求a的值;
(2)若复数z>0,求a的值.
18、(本小题12分)
已知角θ满足 ,求下列各式的值:
(1) ;
(2) .
19、(本小题12分)
已知单位向量 , ,的夹角为 ,向量 ,向量 .
(1)若 // ,求 的值;
(2)若 ,求 .
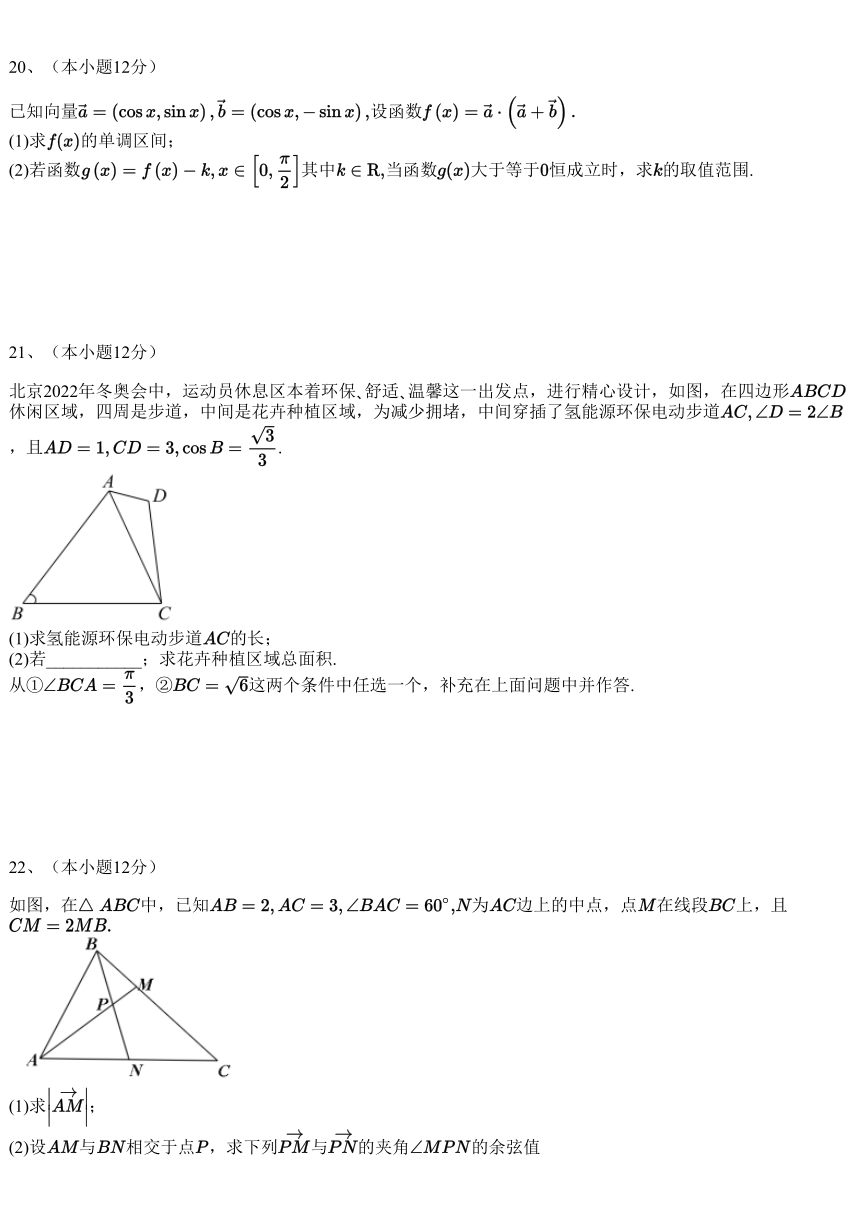
20、(本小题12分)
已知向量 设函数
(1)求 的单调区间;
(2)若函数 其中 当函数 大于等于 恒成立时,求 的取值范围.
21、(本小题12分)
北京2022年冬奥会中,运动员休息区本着环保 舒适 温馨这一出发点,进行精心设计,如图,在四边形
休闲区域,四周是步道,中间是花卉种植区域,为减少拥堵,中间穿插了氢能源环保电动步道
,且 .
(1)求氢能源环保电动步道 的长;
(2)若___________;求花卉种植区域总 面积.
从① ,② 这两个条件中任选一个,补充在上面问题中并作答.
22、(本小题12分)
如图,在 中,已知 为 边上的中点,点 在线段 上,且
(1)求 ;
(2)设 与 相交于点 ,求下列 与 的夹角 的余弦值
参考答案
一、单选题
1、
【答 案】
B
【分析】
因为 i,
所以复数 i对应的点为 ,且在第二象限,
因此正确答案为:B
2、
【答 案】
A
【分析】
,
, ,
.
因此正确答案为:A.
3、
【答 案】
C
【分析】
因为 且 都是第二象限角,
所以 , ,
所以 .
因此正确答案为:C.
4、
【答 案】
C
【分析】
A选项,设 ,则 ,无解,故 三点不共线,A有误;
B选项,设 ,则 ,无解,故 三点不共线,B有误;
C选项, ,
,
故 ,故 三点共线,C无误;
D选项, ,
设 ,则 ,无解,故 三点不共线,D有误.
因此正确答案为:C
5、
【答 案】
C
【分析】
因为 ,
所以所求最小正周期为 .
因此正确答案为:C.
6、
【答 案】
D
【分析】
由余弦定理的: , ,
代入 中,
得 ,
等式两边同乘 得:
,
移项合并得: ,
整理得: ,
即 ,
可得 或 ,
则三角形为等腰三角形或直 角三角形,
因此正确答案为:D.
7、
【答 案】
B
【分析】
通过题意,可得如下图:
由图象可以知 ,所以 ,
所以在运行的一圈里最佳观赏时长为 .
因此正确答案为:B
8、
【答 案】
B
【分析】
解:∵BD:DC:AD=2:3:6,AD⊥BC,
∴tan∠BAD= = ,tan∠CAD= = ,
则tan∠BAC=tan(∠BAD+∠CAD)= =1,
又∠BAC∈(0,π),
则∠BAC= ;
因此正确答案为:B.
二、多选题
9、
【答 案】
B;D
【分析】
A.若 ,则 方向不一定相同,即两向量不一定相等,故不正确;
B. ,则 ,正确;
C. ,则 与 不能比较大小;
D. ,则 ,因此正确.
因此正确答案为:BD.
10、
【答 案】
A;C;D
【分析】
对于A, ,
故A无误;
对于B,
,
,故B有误;
对于C, ,
故C无误;
对于D, ,故D无误;
因此正确答案为:ACD.
11、
【答 案】
B;C
【分析】
, ,解得: .
因此正确答案为:BC.
12、
【答 案】
B;C;D
【分析】
= = = ,故A错,C对,
= = = 7,故B对,
+10 +6 2
7 -24 +36 2
= = ,由于 , ,故 = ,故D对.
3
因此正确答案为:BCD
三、填空题
13、
【答案 】
1
【分析】
设 i R,代入 ,得 ,
设 , ,则 ,
当 时,即 取等号. 即 的最小值是1.
因此正确答案为:1.
14、
【答 案】
/
【分析】
因为 ,
所以
,
因此正确答案为:
15、
【答案 】
【分析】
因为点 , 是线段 的三等分点,则 ,
所以 .
因此正确答案为: .
16、
【答案 】
【分析】
因为 ,
所以三个向量 首 尾相接后,构成一个三角形,如下图所示,
设 ,
因为 与 的夹角为 , 与 的夹角为 ,
所以 ,
所以由正弦定理得 ,得 ,
所以 ,解得 ,
所以 ,
因此正确答案为:
四、解答题
17、
【答 案】
(1)
(2)
【分析】
(1)由于 为纯虚数,
所以 ,可得 .
(2)由于 与 可以比较大小,所以 为实数,且 ,
所以 ,可得 .
18、
【答案 】
(1) ;(2) .
【分析】
,解得 .
(1) .
(2) .
19、
【答案 】
(1) ;(2) .
【分析】
(1)因为 // ,所以存在唯一实数t,使得 ,即 ,
所以 ,解得 ;
(2)由已知得 ,由 得 ,即
+ ,解得 ,
所以 ,所以 ,所以 .
20、
【答案 】
(1)单调递增区间为 , ;单调递减区间为 , ;
(2)
【分析】
(1)∵ ,
令 , ,解得 , ;
令 , ,解得 , ;
∴ 的单调递增区间为 , ;
∴ 的单调递减区间为 , ;
(2)由 ,可得 ,则 ,
所以函数 在 的值域为 .
,即 在 上恒成立,
∴ .
的取值 范围是 .
21、
【答案 】
(1)
(2)答案 见解析
【分析】
(1)利用二倍角公式求出 ,利用余弦定可求 的长;
(2)选①:由正弦定理可求得 ,利用两角和的正弦公式可求得 ,可分别求得 ,
,从而可求花卉种植区域总面积.
选②:利用余弦定理求出 ,利用 面积公式可求得 , ,从而可求花卉种植区域总面积.
(1)
解: . , ,
, , 由余弦定理得 ,
, .
(2)
解:若选①: ,在 中,由正弦定理得 , .
,由(1)知 .代入上式可得 ,解得 ,
,
,
, ,
故 ,
花卉种植区域总面积为 .
若选②: ,在 中,由余弦定理得 ,解得 或
(舍去),
. , ,
, ,
故 ,
花卉种植区域总面积为 .
22、
【答 案】
(1)
(2)
【分析】
(1)设 , ,则 , , , ,
,
,则 ,即 ;
(2) ,同理可知 , ,
∴ ,
∵ ,∴ .
试卷
一、单选题(本大题共8小题,每小题5分,共40分)
1、在复平面内,复数 i对应的点所在的象限是( )
A.第一象限
B.第二象限
C.第三象限
D.第四象限
2、已知 则 ( )
A.
B.
C.
D.
3、已知 且 都是第二象限角,则 ( )
A.
B.
C.
D.
4、设 是平面内的一组基底, ,则( )
A. 三点共线
B. 三点共线
C. 三点共线
D. 三点共线
5、函数 的最小正周期是( )
A.
B.
C.
D.
6、在 中,已知 ,则 的形状是( )
A.等腰三角形
B.直角三角形
C.等边三角形
D.等腰或直角三角形
7、京西某游乐园的摩天轮采用了国内首创的横梁结构,风格更加简约,摩天轮直径88米,最高点A距离地面
100米,匀速运行一圈的时间是18分钟.由于受到周边建筑物的影响,乘客与地面的距离超过34米时,可视为最
佳观赏位置,在运行的一圈里最佳观赏时长为( )
A.10分钟
B.12分钟
C.14分钟
D.16分钟
8、如图,在△ABC中,AD⊥BC,垂足为D,BD:DC:AD=2:3:6,则∠BAC的度数是( )
A.
B.
C.
D.
二、多选题(本大题共4小题,每小题5分,共20分)
9、下列命题中,正确的是( )
A.若 ,则
B.若 ,则
C.若 ,则
D.若 ,则
10、下列化简正确的是( )
A.
B.
C.
D.
11、已知i为虚数单位,复数 i, i,且 ,则实数 的值可为( )
A.
B.
C.
D.
12、如图,设Ox,Oy是平面内相交成60°角的两条数轴, , 分别是与x轴 y轴正方向同向的单位向量.若向量
,则把有序数对 叫做向量 在坐标系xOy中的坐标.若在坐标系xOy中 ,
,则下列结论正确的是( )
A.
B.
C.
D. 与 的夹角为
3
三、填空题(本大题共4小题,每小题5分,共20分)
13、已知i为虚数单位,复数z满足 ,那么 的最小值是 .
14、已知 ,则 .
15、如图,点 , 是线段 的三等分点,以 , 为基底表示 .
16、已知向量 满足 ,且 与 的夹角为 , 与 的夹角为 , 则 .
四、解答题(本大题共6小题,共70分)
17、(本小题10分)
在复平面内,复数 i(其中i为虚数单位, R).
(1)若复数z为纯虚数,求a的值;
(2)若复数z>0,求a的值.
18、(本小题12分)
已知角θ满足 ,求下列各式的值:
(1) ;
(2) .
19、(本小题12分)
已知单位向量 , ,的夹角为 ,向量 ,向量 .
(1)若 // ,求 的值;
(2)若 ,求 .
20、(本小题12分)
已知向量 设函数
(1)求 的单调区间;
(2)若函数 其中 当函数 大于等于 恒成立时,求 的取值范围.
21、(本小题12分)
北京2022年冬奥会中,运动员休息区本着环保 舒适 温馨这一出发点,进行精心设计,如图,在四边形
休闲区域,四周是步道,中间是花卉种植区域,为减少拥堵,中间穿插了氢能源环保电动步道
,且 .
(1)求氢能源环保电动步道 的长;
(2)若___________;求花卉种植区域总 面积.
从① ,② 这两个条件中任选一个,补充在上面问题中并作答.
22、(本小题12分)
如图,在 中,已知 为 边上的中点,点 在线段 上,且
(1)求 ;
(2)设 与 相交于点 ,求下列 与 的夹角 的余弦值
参考答案
一、单选题
1、
【答 案】
B
【分析】
因为 i,
所以复数 i对应的点为 ,且在第二象限,
因此正确答案为:B
2、
【答 案】
A
【分析】
,
, ,
.
因此正确答案为:A.
3、
【答 案】
C
【分析】
因为 且 都是第二象限角,
所以 , ,
所以 .
因此正确答案为:C.
4、
【答 案】
C
【分析】
A选项,设 ,则 ,无解,故 三点不共线,A有误;
B选项,设 ,则 ,无解,故 三点不共线,B有误;
C选项, ,
,
故 ,故 三点共线,C无误;
D选项, ,
设 ,则 ,无解,故 三点不共线,D有误.
因此正确答案为:C
5、
【答 案】
C
【分析】
因为 ,
所以所求最小正周期为 .
因此正确答案为:C.
6、
【答 案】
D
【分析】
由余弦定理的: , ,
代入 中,
得 ,
等式两边同乘 得:
,
移项合并得: ,
整理得: ,
即 ,
可得 或 ,
则三角形为等腰三角形或直 角三角形,
因此正确答案为:D.
7、
【答 案】
B
【分析】
通过题意,可得如下图:
由图象可以知 ,所以 ,
所以在运行的一圈里最佳观赏时长为 .
因此正确答案为:B
8、
【答 案】
B
【分析】
解:∵BD:DC:AD=2:3:6,AD⊥BC,
∴tan∠BAD= = ,tan∠CAD= = ,
则tan∠BAC=tan(∠BAD+∠CAD)= =1,
又∠BAC∈(0,π),
则∠BAC= ;
因此正确答案为:B.
二、多选题
9、
【答 案】
B;D
【分析】
A.若 ,则 方向不一定相同,即两向量不一定相等,故不正确;
B. ,则 ,正确;
C. ,则 与 不能比较大小;
D. ,则 ,因此正确.
因此正确答案为:BD.
10、
【答 案】
A;C;D
【分析】
对于A, ,
故A无误;
对于B,
,
,故B有误;
对于C, ,
故C无误;
对于D, ,故D无误;
因此正确答案为:ACD.
11、
【答 案】
B;C
【分析】
, ,解得: .
因此正确答案为:BC.
12、
【答 案】
B;C;D
【分析】
= = = ,故A错,C对,
= = = 7,故B对,
+10 +6 2
7 -24 +36 2
= = ,由于 , ,故 = ,故D对.
3
因此正确答案为:BCD
三、填空题
13、
【答案 】
1
【分析】
设 i R,代入 ,得 ,
设 , ,则 ,
当 时,即 取等号. 即 的最小值是1.
因此正确答案为:1.
14、
【答 案】
/
【分析】
因为 ,
所以
,
因此正确答案为:
15、
【答案 】
【分析】
因为点 , 是线段 的三等分点,则 ,
所以 .
因此正确答案为: .
16、
【答案 】
【分析】
因为 ,
所以三个向量 首 尾相接后,构成一个三角形,如下图所示,
设 ,
因为 与 的夹角为 , 与 的夹角为 ,
所以 ,
所以由正弦定理得 ,得 ,
所以 ,解得 ,
所以 ,
因此正确答案为:
四、解答题
17、
【答 案】
(1)
(2)
【分析】
(1)由于 为纯虚数,
所以 ,可得 .
(2)由于 与 可以比较大小,所以 为实数,且 ,
所以 ,可得 .
18、
【答案 】
(1) ;(2) .
【分析】
,解得 .
(1) .
(2) .
19、
【答案 】
(1) ;(2) .
【分析】
(1)因为 // ,所以存在唯一实数t,使得 ,即 ,
所以 ,解得 ;
(2)由已知得 ,由 得 ,即
+ ,解得 ,
所以 ,所以 ,所以 .
20、
【答案 】
(1)单调递增区间为 , ;单调递减区间为 , ;
(2)
【分析】
(1)∵ ,
令 , ,解得 , ;
令 , ,解得 , ;
∴ 的单调递增区间为 , ;
∴ 的单调递减区间为 , ;
(2)由 ,可得 ,则 ,
所以函数 在 的值域为 .
,即 在 上恒成立,
∴ .
的取值 范围是 .
21、
【答案 】
(1)
(2)答案 见解析
【分析】
(1)利用二倍角公式求出 ,利用余弦定可求 的长;
(2)选①:由正弦定理可求得 ,利用两角和的正弦公式可求得 ,可分别求得 ,
,从而可求花卉种植区域总面积.
选②:利用余弦定理求出 ,利用 面积公式可求得 , ,从而可求花卉种植区域总面积.
(1)
解: . , ,
, , 由余弦定理得 ,
, .
(2)
解:若选①: ,在 中,由正弦定理得 , .
,由(1)知 .代入上式可得 ,解得 ,
,
,
, ,
故 ,
花卉种植区域总面积为 .
若选②: ,在 中,由余弦定理得 ,解得 或
(舍去),
. , ,
, ,
故 ,
花卉种植区域总面积为 .
22、
【答 案】
(1)
(2)
【分析】
(1)设 , ,则 , , , ,
,
,则 ,即 ;
(2) ,同理可知 , ,
∴ ,
∵ ,∴ .
同课章节目录
