2022~2023学年江西宜春丰城市江西省丰城九中高三上学期理科期末数学试卷(第九中学、宜春一中)(PDF版含解析)
文档属性
| 名称 | 2022~2023学年江西宜春丰城市江西省丰城九中高三上学期理科期末数学试卷(第九中学、宜春一中)(PDF版含解析) |

|
|
| 格式 | |||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-31 14:57:19 | ||
图片预览




文档简介
2022~2023学年江西宜春丰城市江西省丰城九中高三上学期理科期末数学
试卷(第九中学、宜春一中)
一、单选题(本大题共12小题,每小题5分,共60分)
1、集合 的真子集的个数是( )
A.15
B.8
C.7
D.63
2、已知 (i是虚数单位),则 ( )
A.
B.1
C.0
D.i
3、已知 , ,条件 ,条件 ,则 是 的( )
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件
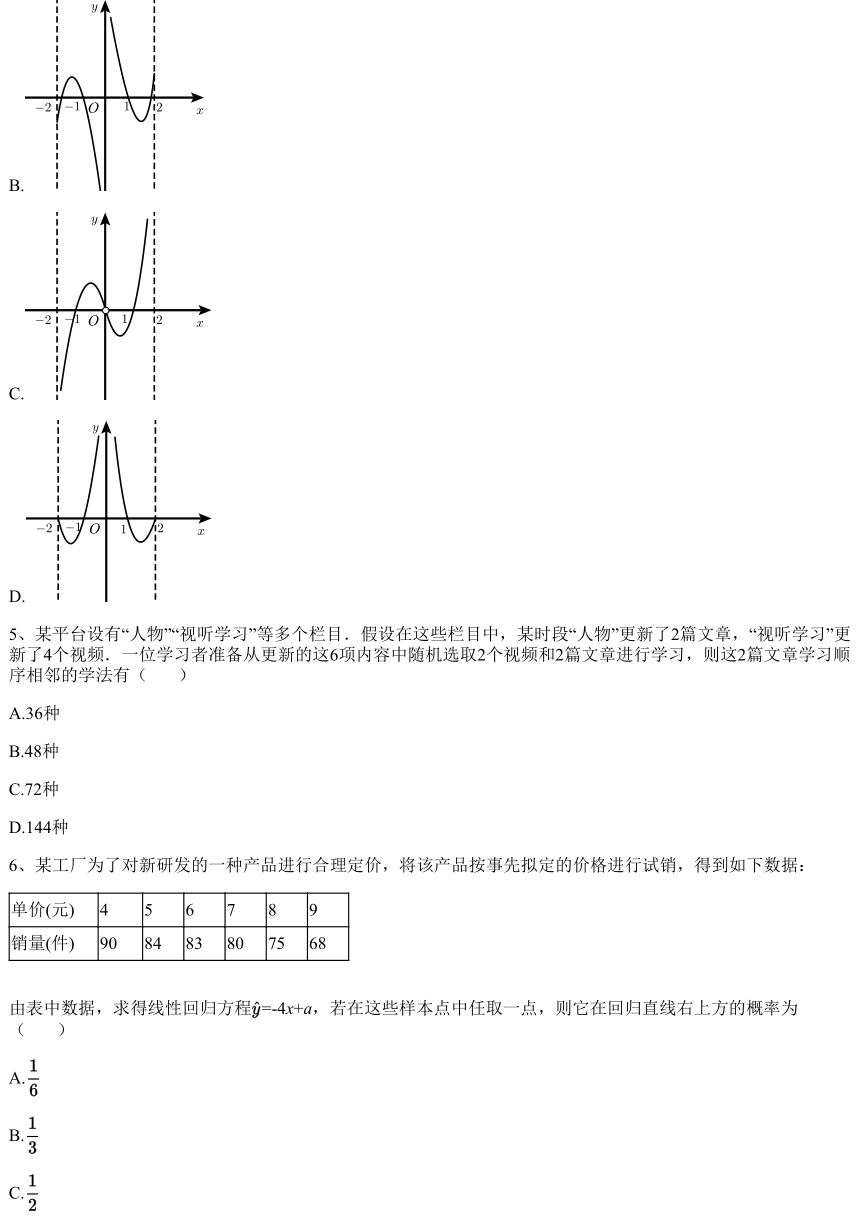
4、函数 的大致图象是( )
O
A.
O
B.
O
C.
O
D.
5、某平台设有“人物”“视听学习”等多个栏目.假设在这些栏目中,某时段“人物”更新了2篇文章,“视听学习”更
新了4个视频.一位学习者准备从更新的这6项内容中随机选取2个视频和2篇文章进行学习,则这2篇文章学习顺
序相邻的学法有( )
A.36种
B.48种
C.72种
D.144种
6、某工厂为了对新研发的一种产品进行合理定价,将该产品按事先拟定的价格进行试销,得到如下数据:
单价(元) 4 5 6 7 8 9
销量(件) 90 84 83 80 75 68
由表中数据,求得线性回归方程 =-4x+a,若在这些样本点中任取一点,则它在回归直线右上方的概率为
( )
A.
B.
C.
D.
7、某中学高三(1)班有50名学生,在一次高三模拟考试中,经统计得:数学成绩 ,则估计
该班数学得分大于120分的学生人数为( )(参考数据:
)
A.16
B.10
C.8
D.2
8、已知定义在R上的函数 为偶函数,当 时, ,则不等式 的解
集为
A.
B.
C.
D.
9、已知圆O的方程为 ,过圆O外一点 作圆O的一条切线 ,切点为A,若 ,则
的最大值为( )
A.
B.
C.
D.
10、在 中,内角A,B,C的对边分别a,b,c,若 , ,则
,则 的取值范围是( )
A.
B.
C.
D.
11、由1,2,3,4,5组成的没有重复数字的五位数,从中任意抽取一个,则其恰好为“前3个数字保持递减,后
3个数字保持递增”(如五位数“43125”,前3个数字“431”保持递减,后3个数字“125”保持递增)的概率是
( )
A.
B.
C.
D.
12、设 ln ,则( )
A.
B.
C.
D.
二、填空题(本大题共4小题,每小题5分,共20分)
13、已知函数 ,则
14、若 ,在 展开式中,各项系数和与二项式系数和之和为65,则展开
式常数项为 .
15、设Sn是等差数列{an}的前n项和,若 ,则 =
16、若函数 图像上有且仅有两对点关于 轴对称,则实数 的取值范围是 .
三、解答题(本大题共7小题,共70分)
17、(本小题8分)
已知函数 , 为奇函数,其图像相邻的对称轴之间的距
离为 .
(1)求函数 的解析式及其减区间;
(2)在 中,角A、B、C对应的边为a、b、c,若 , , ,求 .
18、(本小题8分)
根据11月份中国某信息网发布的我国A市2021年上半年新锐品牌人群用户(新锐品牌人群,指在指定周期内浏
览新锐品牌相关内容以及商品详情页的人群)性别分析数据,得到男性、女性用户比例为 .A市对购买家电
类新锐品牌人群中随机调查了100位男性顾客和100位女性顾客,统计出每位顾客购买家电消费金额,根据这些
数据得到如下的频数分布表:
消费金(元)
女性顾客人数 50 30 10 6 4
男性顾客人数 20 40 24 10 6
(1)若以我国A市2021年上半年新锐品牌人群用户性别分析数据作为A市抽取新锐品牌人群中性别概率,从A市新
锐品牌人群中随机抽取4人,X为4人中男性的人数,求X的数学期望.
(2)根据A市统计购买家电消费金额数据频数分布表,完成下列 列联 表,并根据列联表,判断是否有 的
把握认为购买家电类新锐品牌人群消费金额千元以上与性别有关?
不超千元 千元以上 合计
女性顾客
男性顾客
合计
附: ,
0.05 0.01 0.001
k 3.841 6.635 10.828
19、(本小题8分)
已知数列 满足 * ,且 .
(1)证明: 是等比数列,并求 的通项公式;
(2)在① ;② log ;③ 这三个条件中任选一个补充在下面横线上,并加以解
答.已知数列 满足__________,求 的前 项和 .(如果选择多个条件分别解答,按第一个解答计分)
20、(本小题10分)
甲、乙两支女子排球队进行排球比赛,每场比赛采用“5局3胜制”(即有一支球队先胜3局即获胜,比赛结束),
假设在每局比赛中,甲队获胜的概率为 ,乙队获胜的概率为 ,各局比赛的结果相互独立.
(1)求乙队获胜的概率;
(2)设比赛结束时甲队和乙 队共进行了 局比赛,求随机变量 的分布列及数学期望.
21、(本小题12分)
已知函数 .
(1)当 , 时,讨论函数 的单调性;
(2)若 ,且 ,若 ,求实数的m最大值.
22、(本小题12分)
已知在平面直角坐标系 中,曲线 的参数方程为 ( 为参数).以 为极点, 轴的非负半轴为
极轴建立极坐标系,已知曲线 : 和 : ,曲线 分别交 , 于 , 两点.
(1)求曲线 的极坐标方程和曲线 的直角坐标方程;
(2)求 的面积.
23、(本小题12分)
己知函数 .
(1)解关于x的不等式 ;
(2)记 的最小值为m,若a、b、c都是正实数,且 ,求证: .
参考答案
一、单选题
1、
【答 案】
C
【分析】
由于 ,
,又 ,
,
,即 集合 ,
该集合的所有真子集为 ,
该集合的真子集个数为 ,
因此正确答案为:C.
2、
【答 案】
B
【分析】
通过题意 ,
因此正确答案为:B
3、
【答 案】
A
【分析】
因 , ,由 得: ,则 ,
当且仅当 ,即 , 时取等号,因此, ,
因 , ,由 ,取 ,则 , ,即 , ,
所以 是 的充分不必要条件.
因此正确答案为:A
4、
【答 案】
A
【分析】
由 ,可得 且 ,
故函数 的定义域为 ,
,即函数 为奇函数,排除D选项;
当 时, , ,
则 ,则 ,排除C选项;
时, ,排除B选项.
故选:A.
5、
【答 案】
C
【分析】
通过题意,从4个视频中选2个有C 种方法,
2篇文章全选有C 种方法,
2篇文章要相邻则可以先捆绑看成1个元素,三个学习内容全排列有A 种方法,
最后需要对捆绑元素进行松绑全排列有A 种方法,
故满足题意的学法有C C A A (种).
因此正确答案为:C
6、
【答 案】
C
【分析】
因为 ,
,
所以 ,即
满足 的点有 ,共3个
所以在这些样本点中任取一点,则它在回归直线右上方的概率为 ,
因此正确答案为:C
7、
【答 案】
C
【分析】
因为数学成绩 ,所以 ,因此由
所以有
,
估计该班数学得分大于120分的学生人数为 ,
因此正确答案为:C
8、
【答 案】
D
【分析】
当 时, 为增函数, 也是增函数,故 为增函数.
又因为函数 为偶函数,所以 的图像关于直线 对称.
因为 ,故 即 ,
两边平方后得到 即 ,
因此正确答案为D.
9、
【答 案】
A
【分析】
因为 为圆O的一条切线,故 ,
则 ,解得 ,
由勾股定理得 ,即 ,
可设 , ,
则 ,其中 ,
故 的最大值为 .
因此正确答案为:A
10、
【答 案】
C
【分析】
通过题意知 ,
由正弦定理知 ,
,
又 , ,
故在 中, .
,
,
又 由余弦定理可得: ,
,
由 ,当且仅当 时取等号,
, 的最大值为 .
又 ,故 的取值范围是 ,
11、
【答 案】
A
【分析】
由1,2,3,4,5组成的没有重复数字的五位数共A 个,前3个数字保持递减,后3个数字保持递增,说
明中间数字为1;
在剩余的四个数字 中任取两个数字,按照递减顺序,仅有一种排列方式放置在首两位(或末两位),则剩余两位
数字排列方式唯一确定,放置在最后两位(或首两位).C \times 1
因此“前3个数字保持递减,后3个数字保持递增”的五位数有C 个,
所以所求的概率 .
因此正确答案为:A.
12、
【答案 】
B
【分析】
解:
设
所以
所以 所以 单 调递增, 单调递减,
所以
当 时, ,所以 在 上恒成立,
所以函数 在 单调递增,
所以 ,
所以 .
所以 .
设 ,
所以 ,
设 ,
所以 在 上单调递减,
所以 ,
所以 ,所以函数 在 上单调递减,
所以 ,所以 .
故 .
因此正确答案 为:B
二、填空题
13、
【答案 】
【分析】
因为 ,所以 ,从而得
.
因此正确答案为: .
14、
【答 案】
60
【分析】
,
,
令 ,故得系数之和为1,而二项式系数和为
由二项式系数和以及项之和可得 ,
由于二项式展开式的通项为 ,
令 ,所以常数项为 ,
因此正确答案为:60
15、
【答 案】
【分析】
试题分析:若Sn是等差数列{an}的前n项和,
则 也是等差数列;
所以 也是等差数列,
由 可设 ,则 ,
于是可得相邻三项和依次为 ,
即 ,
所以 .
16、
【答案 】
【分析】
当 时, ,其关于 轴对称的函数为 ,
因为函数 图像上有且仅有两对点关于 轴对称,所以,由 ,
得到 ,所以 有两个不同的交点,
令 ,则 ,所以, 在区间 上单调递减,在区间
上单调递增,所以 ,
又当 时, ,当 时, ,故 的图象如下图所示,
所以 ,
因此正确答案 为: .
三、解答题
17、
【答 案】
(1) , 的减区间为 ;
(2) .
【分析】
(1) ,
由函数 相邻的对称轴之间的距离为 , ,
所以 ,又 ,故
∴ ,
又∵ 为奇函数,∴ ,即 ,
得 ,即 ,而 ,故 ,
因为函数 的定义域为 ,定义域关于原点对称,
又 ,所以 为奇函数,满足要求,
令 ,得 ,
∴ 的减区间为 ;
(2)由(1)可知 ,又 ,
所以 ,即 ,
∵ ,∴ ,
∴ ,即 ,
由正弦定理可得 ,又 , ,
所以 ,所以 ,
因为 ,所以 ,所以 ,
所以 ,
所以 .
18、
【答案 】
(1)3
(2)列 联表见解析;有 的把握.
【分析】
(1)通过题意知以我国A市2021年上半年新锐品牌人群用户性别分析数据作为A市抽取新锐品牌人群中性别概
率,
男性、女性用户比例为 ,故从A市新锐品牌人群中随机抽取1人为男性的概率为 ,
则随机抽取4人,X为4人中男性的人数,则 ,
故X的数学期望为 .
(2)通过题意可得列联表:
不超千元 千元以上 合计
女性顾客 80 20 100
男性顾客 60 40 100
合计 140 60 200
故 ,
故有 的把握认为购买家电类新锐品牌人群消费金额千元以上与性别有关.
19、
【答案 】
(1)证明见解析,
(2)答案见解析
【分析】
(1)利用递推公式,结合等比数列的定义和通项公式进行求解即可;
(2)若选①:利用错位相减法进行求解即可;
若选②:根据对数的运算性质,结合等差数列前 项和公式进行求解即可;
若选③:根据裂项相消法进行求解即可.
【详解】
(1)因为 ,
所以 ,又 ,于是 ,
所以 是以4为首项2为公比的等比数列.
所以 ,两边除以 得, .
又 ,所以 是以2为首项1为公差的等差数列.
所以 ,即 .
(2)若选①: ,即 .
因为 ,
所以 .
两式相减得,
,
所以 .
若选②: log ,即 log log log .
所以 log log log
log
log
若选③: ,即 .
所以
20、
【答案 】
(1)
(2)分布列见解析,
【分析】
(1)通过题意知,比赛三局且乙队获胜的概率 ,
比赛四局且乙队获胜的概率为 ,
比赛五局且乙队获胜的概率为 ,
所以乙队获胜的概率为 .
(2)通过题意随机变量 的可能取值为 , , ,
则 ,
,
,
所以随机变量 的分布列为
3 4 5
所以 .
21、
【答 案】
(1)答案见解析;
(2)m最大值为 .
【分析】
(1)因为
当 , 时,可得 ,
令 ,解得 或2,
当 时,
当 时 , ,函数 在 上单调递增,
当 时, ,函数 在在 上单调递减 ,
当 时, ,函数 在 上单调递增;
当 时, ,当且仅当 时取等号,
故函数 在 上单调递增;
当 时,
当 时 ,函数 在 上单调递增,
当 时 ,函数 在 上单调递减,
当 时 ,函数 在 上单调递增,
(2)当 时, .
所以方程 有两个正根 ,
且 ,解得 ,
通过题意得
,
令 .
则 在 上单调递椷,
,
,
因为 恒 成立,
所以 ,
所以m最大值为 .
22、
【答案 】
(1) , ;
(2) .
【分析】
(1)解:由参数方程 ( 为参数),可得
消去 可得 的普通方程为 .
又 代入 ,可得 ,
即 的极坐标方程为 ;
由极坐标方程 ,可得 ,
所以 的直角坐标方程为 .
(2)解:设 ,将 代入 ,可得 ,所以 .
设 ,同理可知 ,
所以 .
23、
【答 案】
(1)不等式 的解集为 或 ;
(2)证明见解析.
【分析】
(1)由 ,可得 ,
当 时,由 ,解得 ,此时 ;
当 时, ,此时不等式 无解;
当 时,由 ,解得 ,此时 .
综上所述,不等式 的解集为 或 .
(2)由绝对值三角不等式可得 ,
当且仅当 时等号成立,
所以 的最小值为 ,故 ,
通过题意可知,正实数 、 、 满足 ,
由柯西不等式可得 ,
当且仅当 时,等号成立,故原不等式得证.
试卷(第九中学、宜春一中)
一、单选题(本大题共12小题,每小题5分,共60分)
1、集合 的真子集的个数是( )
A.15
B.8
C.7
D.63
2、已知 (i是虚数单位),则 ( )
A.
B.1
C.0
D.i
3、已知 , ,条件 ,条件 ,则 是 的( )
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件
4、函数 的大致图象是( )
O
A.
O
B.
O
C.
O
D.
5、某平台设有“人物”“视听学习”等多个栏目.假设在这些栏目中,某时段“人物”更新了2篇文章,“视听学习”更
新了4个视频.一位学习者准备从更新的这6项内容中随机选取2个视频和2篇文章进行学习,则这2篇文章学习顺
序相邻的学法有( )
A.36种
B.48种
C.72种
D.144种
6、某工厂为了对新研发的一种产品进行合理定价,将该产品按事先拟定的价格进行试销,得到如下数据:
单价(元) 4 5 6 7 8 9
销量(件) 90 84 83 80 75 68
由表中数据,求得线性回归方程 =-4x+a,若在这些样本点中任取一点,则它在回归直线右上方的概率为
( )
A.
B.
C.
D.
7、某中学高三(1)班有50名学生,在一次高三模拟考试中,经统计得:数学成绩 ,则估计
该班数学得分大于120分的学生人数为( )(参考数据:
)
A.16
B.10
C.8
D.2
8、已知定义在R上的函数 为偶函数,当 时, ,则不等式 的解
集为
A.
B.
C.
D.
9、已知圆O的方程为 ,过圆O外一点 作圆O的一条切线 ,切点为A,若 ,则
的最大值为( )
A.
B.
C.
D.
10、在 中,内角A,B,C的对边分别a,b,c,若 , ,则
,则 的取值范围是( )
A.
B.
C.
D.
11、由1,2,3,4,5组成的没有重复数字的五位数,从中任意抽取一个,则其恰好为“前3个数字保持递减,后
3个数字保持递增”(如五位数“43125”,前3个数字“431”保持递减,后3个数字“125”保持递增)的概率是
( )
A.
B.
C.
D.
12、设 ln ,则( )
A.
B.
C.
D.
二、填空题(本大题共4小题,每小题5分,共20分)
13、已知函数 ,则
14、若 ,在 展开式中,各项系数和与二项式系数和之和为65,则展开
式常数项为 .
15、设Sn是等差数列{an}的前n项和,若 ,则 =
16、若函数 图像上有且仅有两对点关于 轴对称,则实数 的取值范围是 .
三、解答题(本大题共7小题,共70分)
17、(本小题8分)
已知函数 , 为奇函数,其图像相邻的对称轴之间的距
离为 .
(1)求函数 的解析式及其减区间;
(2)在 中,角A、B、C对应的边为a、b、c,若 , , ,求 .
18、(本小题8分)
根据11月份中国某信息网发布的我国A市2021年上半年新锐品牌人群用户(新锐品牌人群,指在指定周期内浏
览新锐品牌相关内容以及商品详情页的人群)性别分析数据,得到男性、女性用户比例为 .A市对购买家电
类新锐品牌人群中随机调查了100位男性顾客和100位女性顾客,统计出每位顾客购买家电消费金额,根据这些
数据得到如下的频数分布表:
消费金(元)
女性顾客人数 50 30 10 6 4
男性顾客人数 20 40 24 10 6
(1)若以我国A市2021年上半年新锐品牌人群用户性别分析数据作为A市抽取新锐品牌人群中性别概率,从A市新
锐品牌人群中随机抽取4人,X为4人中男性的人数,求X的数学期望.
(2)根据A市统计购买家电消费金额数据频数分布表,完成下列 列联 表,并根据列联表,判断是否有 的
把握认为购买家电类新锐品牌人群消费金额千元以上与性别有关?
不超千元 千元以上 合计
女性顾客
男性顾客
合计
附: ,
0.05 0.01 0.001
k 3.841 6.635 10.828
19、(本小题8分)
已知数列 满足 * ,且 .
(1)证明: 是等比数列,并求 的通项公式;
(2)在① ;② log ;③ 这三个条件中任选一个补充在下面横线上,并加以解
答.已知数列 满足__________,求 的前 项和 .(如果选择多个条件分别解答,按第一个解答计分)
20、(本小题10分)
甲、乙两支女子排球队进行排球比赛,每场比赛采用“5局3胜制”(即有一支球队先胜3局即获胜,比赛结束),
假设在每局比赛中,甲队获胜的概率为 ,乙队获胜的概率为 ,各局比赛的结果相互独立.
(1)求乙队获胜的概率;
(2)设比赛结束时甲队和乙 队共进行了 局比赛,求随机变量 的分布列及数学期望.
21、(本小题12分)
已知函数 .
(1)当 , 时,讨论函数 的单调性;
(2)若 ,且 ,若 ,求实数的m最大值.
22、(本小题12分)
已知在平面直角坐标系 中,曲线 的参数方程为 ( 为参数).以 为极点, 轴的非负半轴为
极轴建立极坐标系,已知曲线 : 和 : ,曲线 分别交 , 于 , 两点.
(1)求曲线 的极坐标方程和曲线 的直角坐标方程;
(2)求 的面积.
23、(本小题12分)
己知函数 .
(1)解关于x的不等式 ;
(2)记 的最小值为m,若a、b、c都是正实数,且 ,求证: .
参考答案
一、单选题
1、
【答 案】
C
【分析】
由于 ,
,又 ,
,
,即 集合 ,
该集合的所有真子集为 ,
该集合的真子集个数为 ,
因此正确答案为:C.
2、
【答 案】
B
【分析】
通过题意 ,
因此正确答案为:B
3、
【答 案】
A
【分析】
因 , ,由 得: ,则 ,
当且仅当 ,即 , 时取等号,因此, ,
因 , ,由 ,取 ,则 , ,即 , ,
所以 是 的充分不必要条件.
因此正确答案为:A
4、
【答 案】
A
【分析】
由 ,可得 且 ,
故函数 的定义域为 ,
,即函数 为奇函数,排除D选项;
当 时, , ,
则 ,则 ,排除C选项;
时, ,排除B选项.
故选:A.
5、
【答 案】
C
【分析】
通过题意,从4个视频中选2个有C 种方法,
2篇文章全选有C 种方法,
2篇文章要相邻则可以先捆绑看成1个元素,三个学习内容全排列有A 种方法,
最后需要对捆绑元素进行松绑全排列有A 种方法,
故满足题意的学法有C C A A (种).
因此正确答案为:C
6、
【答 案】
C
【分析】
因为 ,
,
所以 ,即
满足 的点有 ,共3个
所以在这些样本点中任取一点,则它在回归直线右上方的概率为 ,
因此正确答案为:C
7、
【答 案】
C
【分析】
因为数学成绩 ,所以 ,因此由
所以有
,
估计该班数学得分大于120分的学生人数为 ,
因此正确答案为:C
8、
【答 案】
D
【分析】
当 时, 为增函数, 也是增函数,故 为增函数.
又因为函数 为偶函数,所以 的图像关于直线 对称.
因为 ,故 即 ,
两边平方后得到 即 ,
因此正确答案为D.
9、
【答 案】
A
【分析】
因为 为圆O的一条切线,故 ,
则 ,解得 ,
由勾股定理得 ,即 ,
可设 , ,
则 ,其中 ,
故 的最大值为 .
因此正确答案为:A
10、
【答 案】
C
【分析】
通过题意知 ,
由正弦定理知 ,
,
又 , ,
故在 中, .
,
,
又 由余弦定理可得: ,
,
由 ,当且仅当 时取等号,
, 的最大值为 .
又 ,故 的取值范围是 ,
11、
【答 案】
A
【分析】
由1,2,3,4,5组成的没有重复数字的五位数共A 个,前3个数字保持递减,后3个数字保持递增,说
明中间数字为1;
在剩余的四个数字 中任取两个数字,按照递减顺序,仅有一种排列方式放置在首两位(或末两位),则剩余两位
数字排列方式唯一确定,放置在最后两位(或首两位).C \times 1
因此“前3个数字保持递减,后3个数字保持递增”的五位数有C 个,
所以所求的概率 .
因此正确答案为:A.
12、
【答案 】
B
【分析】
解:
设
所以
所以 所以 单 调递增, 单调递减,
所以
当 时, ,所以 在 上恒成立,
所以函数 在 单调递增,
所以 ,
所以 .
所以 .
设 ,
所以 ,
设 ,
所以 在 上单调递减,
所以 ,
所以 ,所以函数 在 上单调递减,
所以 ,所以 .
故 .
因此正确答案 为:B
二、填空题
13、
【答案 】
【分析】
因为 ,所以 ,从而得
.
因此正确答案为: .
14、
【答 案】
60
【分析】
,
,
令 ,故得系数之和为1,而二项式系数和为
由二项式系数和以及项之和可得 ,
由于二项式展开式的通项为 ,
令 ,所以常数项为 ,
因此正确答案为:60
15、
【答 案】
【分析】
试题分析:若Sn是等差数列{an}的前n项和,
则 也是等差数列;
所以 也是等差数列,
由 可设 ,则 ,
于是可得相邻三项和依次为 ,
即 ,
所以 .
16、
【答案 】
【分析】
当 时, ,其关于 轴对称的函数为 ,
因为函数 图像上有且仅有两对点关于 轴对称,所以,由 ,
得到 ,所以 有两个不同的交点,
令 ,则 ,所以, 在区间 上单调递减,在区间
上单调递增,所以 ,
又当 时, ,当 时, ,故 的图象如下图所示,
所以 ,
因此正确答案 为: .
三、解答题
17、
【答 案】
(1) , 的减区间为 ;
(2) .
【分析】
(1) ,
由函数 相邻的对称轴之间的距离为 , ,
所以 ,又 ,故
∴ ,
又∵ 为奇函数,∴ ,即 ,
得 ,即 ,而 ,故 ,
因为函数 的定义域为 ,定义域关于原点对称,
又 ,所以 为奇函数,满足要求,
令 ,得 ,
∴ 的减区间为 ;
(2)由(1)可知 ,又 ,
所以 ,即 ,
∵ ,∴ ,
∴ ,即 ,
由正弦定理可得 ,又 , ,
所以 ,所以 ,
因为 ,所以 ,所以 ,
所以 ,
所以 .
18、
【答案 】
(1)3
(2)列 联表见解析;有 的把握.
【分析】
(1)通过题意知以我国A市2021年上半年新锐品牌人群用户性别分析数据作为A市抽取新锐品牌人群中性别概
率,
男性、女性用户比例为 ,故从A市新锐品牌人群中随机抽取1人为男性的概率为 ,
则随机抽取4人,X为4人中男性的人数,则 ,
故X的数学期望为 .
(2)通过题意可得列联表:
不超千元 千元以上 合计
女性顾客 80 20 100
男性顾客 60 40 100
合计 140 60 200
故 ,
故有 的把握认为购买家电类新锐品牌人群消费金额千元以上与性别有关.
19、
【答案 】
(1)证明见解析,
(2)答案见解析
【分析】
(1)利用递推公式,结合等比数列的定义和通项公式进行求解即可;
(2)若选①:利用错位相减法进行求解即可;
若选②:根据对数的运算性质,结合等差数列前 项和公式进行求解即可;
若选③:根据裂项相消法进行求解即可.
【详解】
(1)因为 ,
所以 ,又 ,于是 ,
所以 是以4为首项2为公比的等比数列.
所以 ,两边除以 得, .
又 ,所以 是以2为首项1为公差的等差数列.
所以 ,即 .
(2)若选①: ,即 .
因为 ,
所以 .
两式相减得,
,
所以 .
若选②: log ,即 log log log .
所以 log log log
log
log
若选③: ,即 .
所以
20、
【答案 】
(1)
(2)分布列见解析,
【分析】
(1)通过题意知,比赛三局且乙队获胜的概率 ,
比赛四局且乙队获胜的概率为 ,
比赛五局且乙队获胜的概率为 ,
所以乙队获胜的概率为 .
(2)通过题意随机变量 的可能取值为 , , ,
则 ,
,
,
所以随机变量 的分布列为
3 4 5
所以 .
21、
【答 案】
(1)答案见解析;
(2)m最大值为 .
【分析】
(1)因为
当 , 时,可得 ,
令 ,解得 或2,
当 时,
当 时 , ,函数 在 上单调递增,
当 时, ,函数 在在 上单调递减 ,
当 时, ,函数 在 上单调递增;
当 时, ,当且仅当 时取等号,
故函数 在 上单调递增;
当 时,
当 时 ,函数 在 上单调递增,
当 时 ,函数 在 上单调递减,
当 时 ,函数 在 上单调递增,
(2)当 时, .
所以方程 有两个正根 ,
且 ,解得 ,
通过题意得
,
令 .
则 在 上单调递椷,
,
,
因为 恒 成立,
所以 ,
所以m最大值为 .
22、
【答案 】
(1) , ;
(2) .
【分析】
(1)解:由参数方程 ( 为参数),可得
消去 可得 的普通方程为 .
又 代入 ,可得 ,
即 的极坐标方程为 ;
由极坐标方程 ,可得 ,
所以 的直角坐标方程为 .
(2)解:设 ,将 代入 ,可得 ,所以 .
设 ,同理可知 ,
所以 .
23、
【答 案】
(1)不等式 的解集为 或 ;
(2)证明见解析.
【分析】
(1)由 ,可得 ,
当 时,由 ,解得 ,此时 ;
当 时, ,此时不等式 无解;
当 时,由 ,解得 ,此时 .
综上所述,不等式 的解集为 或 .
(2)由绝对值三角不等式可得 ,
当且仅当 时等号成立,
所以 的最小值为 ,故 ,
通过题意可知,正实数 、 、 满足 ,
由柯西不等式可得 ,
当且仅当 时,等号成立,故原不等式得证.
同课章节目录
