初中数学人教版八年级下册18.2.2.2 菱形的判定 同步练习(含答案)
文档属性
| 名称 | 初中数学人教版八年级下册18.2.2.2 菱形的判定 同步练习(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 161.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-31 11:03:04 | ||
图片预览

文档简介
第十八章 平行四边形
18.2.2 菱形
第2课时 菱形的判定
一、选择题
1.下列条件中,能判定四边形是菱形的是( )
A.两条对角线相等 B.两条对角线互相垂直
C.两条对角线互相垂直平分 D.两条对角线互相平分且相等
2.在平行四边形ABCD中添加下列条件,不能判定四边形ABCD是菱形的是( )
A.AB=BC B.AC⊥BD C.AC=BD D.∠ABD=∠CBD
3.在数学活动课上,为探究四边形瓷砖是否为菱形,以下拟定的测量方案,正确的是( )
A.测量一组对边是否平行且相等 B.测量四个内角是否相等
C.测量两条对角线是否互相垂直 D.测量四条边是否相等
4.用直尺和圆规作一个以线段AB为边的菱形,作图痕迹如图所示,能得到四边形ABCD是菱形的依据是( )
A.一组邻边相等的四边形是菱形 B.四边相等的四边形是菱形
C.对角线互相垂直的平行四边形是菱形
D.每条对角线平分一组对角的平行四边形是菱形
5.如图,在四边形ABCD中,E、F、G、H分别是AB、BD、CD、AC的中点,要使四边形EFGH是菱形,则四边形ABCD只需要满足一个条件,是( )
A.AD=BC B.AC=BD C.AB=CD D.AD=CD
6.如图,在△ABC中,D是BC边的中点,点E,F分别在线段AD及其延长线上,DE=DF.在下列条件中,使四边形BECF是菱形的是( )
A.EB⊥EC B.AB⊥AC C.AB=AC D.BF∥CE
二、填空题
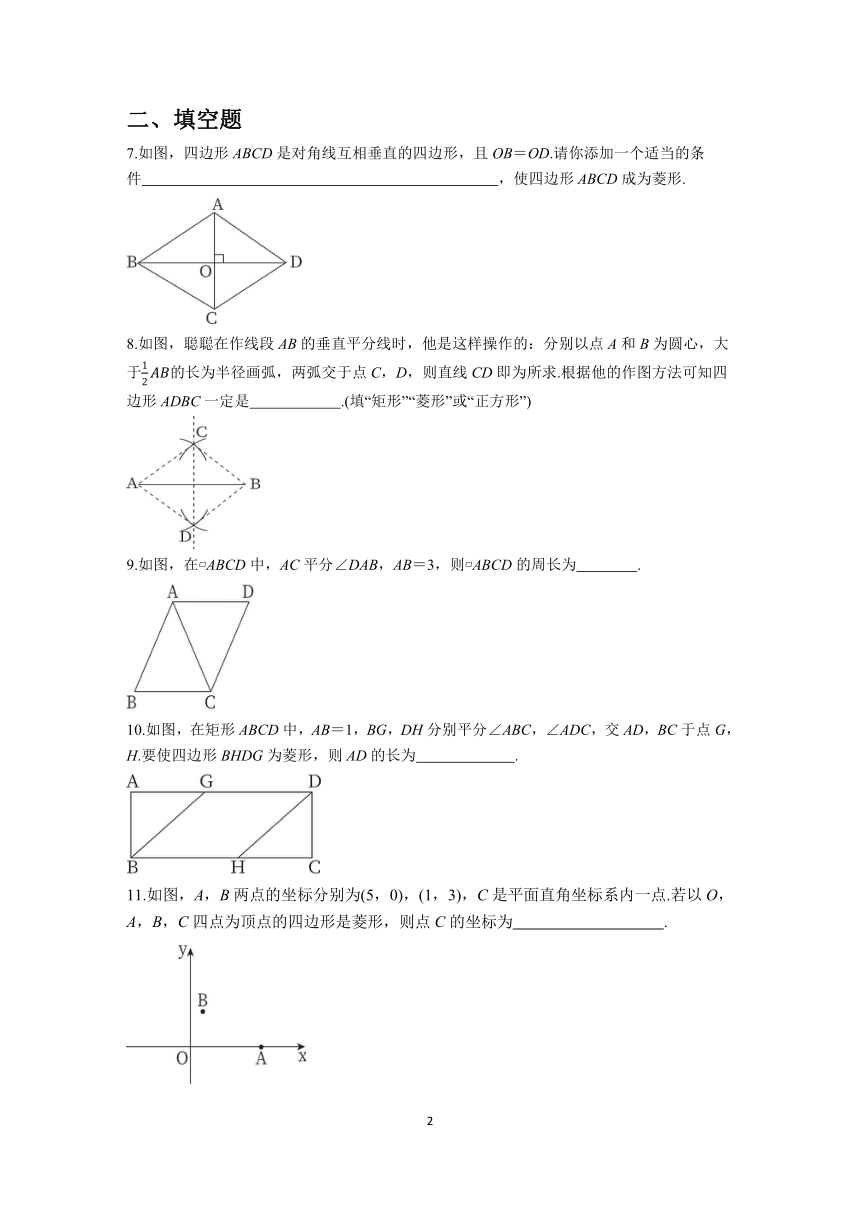
7.如图,四边形ABCD是对角线互相垂直的四边形,且OB=OD.请你添加一个适当的条件 ,使四边形ABCD成为菱形.
8.如图,聪聪在作线段AB的垂直平分线时,他是这样操作的:分别以点A和B为圆心,大于的长为半径画弧,两弧交于点C,D,则直线CD即为所求.根据他的作图方法可知四边形ADBC一定是 .(填“矩形”“菱形”或“正方形”)
9.如图,在 ABCD中,AC平分∠DAB,AB=3,则 ABCD的周长为 .
10.如图,在矩形ABCD中,AB=1,BG,DH分别平分∠ABC,∠ADC,交AD,BC于点G,H.要使四边形BHDG为菱形,则AD的长为 .
11.如图,A,B两点的坐标分别为(5,0),(1,3),C是平面直角坐标系内一点.若以O,A,B,C四点为顶点的四边形是菱形,则点C的坐标为 .
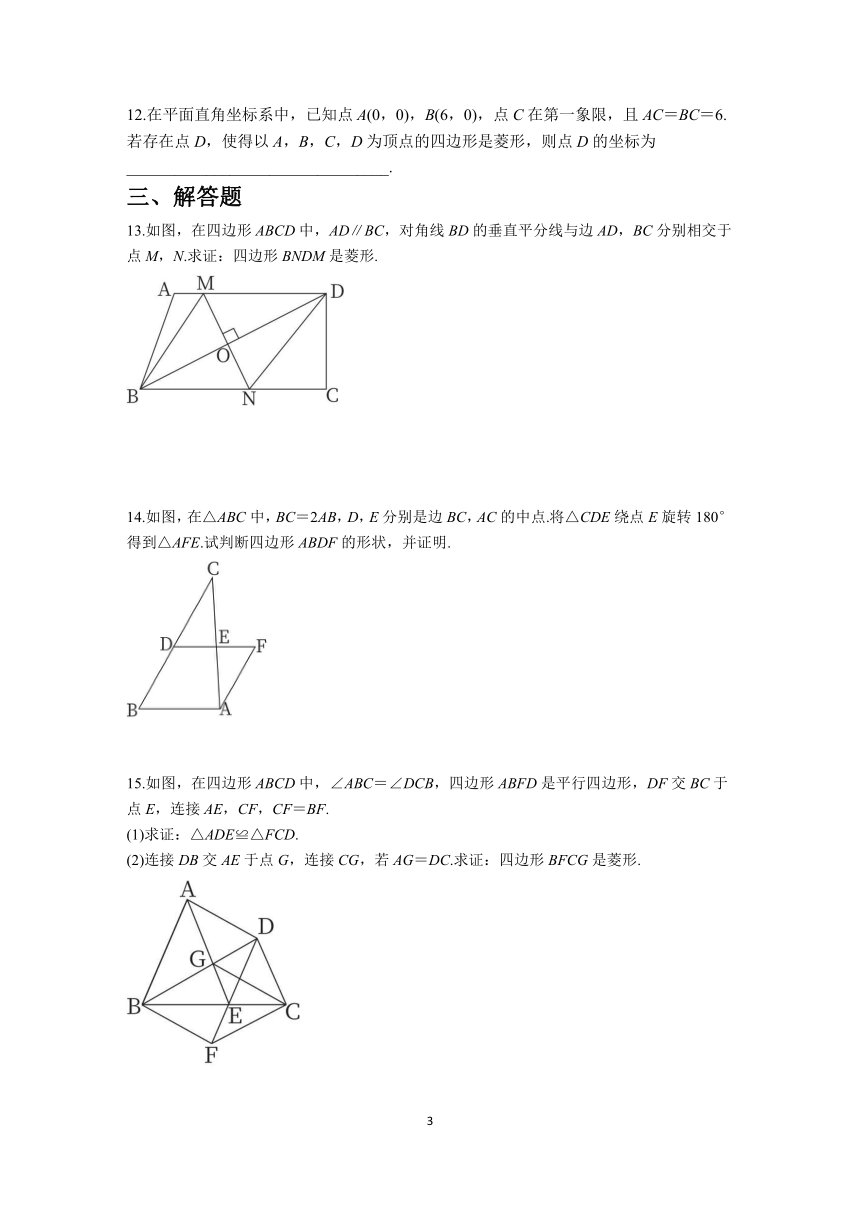
12.在平面直角坐标系中,已知点A(0,0),B(6,0),点C在第一象限,且AC=BC=6.若存在点D,使得以A,B,C,D为顶点的四边形是菱形,则点D的坐标为_________________________________.
三、解答题
13.如图,在四边形ABCD中,AD∥BC,对角线BD的垂直平分线与边AD,BC分别相交于点M,N.求证:四边形BNDM是菱形.
14.如图,在△ABC中,BC=2AB,D,E分别是边BC,AC的中点.将△CDE绕点E旋转180°得到△AFE.试判断四边形ABDF的形状,并证明.
15.如图,在四边形ABCD中,∠ABC=∠DCB,四边形ABFD是平行四边形,DF交BC于点E,连接AE,CF,CF=BF.
(1)求证:△ADE≌△FCD.
(2)连接DB交AE于点G,连接CG,若AG=DC.求证:四边形BFCG是菱形.
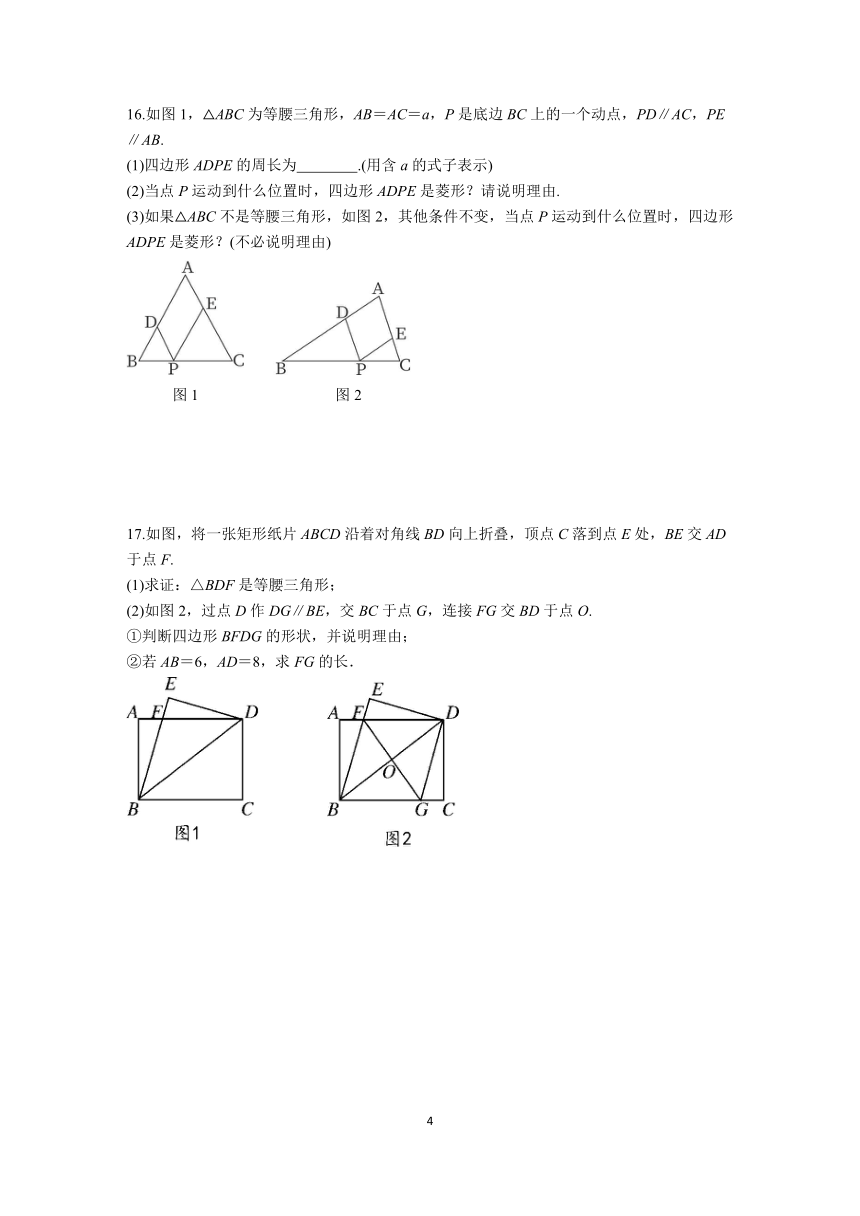
16.如图1,△ABC为等腰三角形,AB=AC=a,P是底边BC上的一个动点,PD∥AC,PE∥AB.
(1)四边形ADPE的周长为 .(用含a的式子表示)
(2)当点P运动到什么位置时,四边形ADPE是菱形?请说明理由.
(3)如果△ABC不是等腰三角形,如图2,其他条件不变,当点P运动到什么位置时,四边形ADPE是菱形?(不必说明理由)
图1 图2
17.如图,将一张矩形纸片ABCD沿着对角线BD向上折叠,顶点C落到点E处,BE交AD于点F.
(1)求证:△BDF是等腰三角形;
(2)如图2,过点D作DG∥BE,交BC于点G,连接FG交BD于点O.
①判断四边形BFDG的形状,并说明理由;
②若AB=6,AD=8,求FG的长.
1
参考答案
一、选择题
1.下列条件中,能判定四边形是菱形的是( C )
A.两条对角线相等 B.两条对角线互相垂直
C.两条对角线互相垂直平分 D.两条对角线互相平分且相等
2.在平行四边形ABCD中添加下列条件,不能判定四边形ABCD是菱形的是( C )
A.AB=BC B.AC⊥BD C.AC=BD D.∠ABD=∠CBD
3.在数学活动课上,为探究四边形瓷砖是否为菱形,以下拟定的测量方案,正确的是( D )
A.测量一组对边是否平行且相等 B.测量四个内角是否相等
C.测量两条对角线是否互相垂直 D.测量四条边是否相等
4.用直尺和圆规作一个以线段AB为边的菱形,作图痕迹如图所示,能得到四边形ABCD是菱形的依据是( B )
A.一组邻边相等的四边形是菱形 B.四边相等的四边形是菱形
C.对角线互相垂直的平行四边形是菱形
D.每条对角线平分一组对角的平行四边形是菱形
5.如图,在四边形ABCD中,E、F、G、H分别是AB、BD、CD、AC的中点,要使四边形EFGH是菱形,则四边形ABCD只需要满足一个条件,是( A )
A.AD=BC B.AC=BD C.AB=CD D.AD=CD
6.如图,在△ABC中,D是BC边的中点,点E,F分别在线段AD及其延长线上,DE=DF.在下列条件中,使四边形BECF是菱形的是( C )
A.EB⊥EC B.AB⊥AC C.AB=AC D.BF∥CE
二、填空题
7.如图,四边形ABCD是对角线互相垂直的四边形,且OB=OD.请你添加一个适当的条件 ,使四边形ABCD成为菱形.
【答案】 OA=OC(答案不唯一,合理即可)
8.如图,聪聪在作线段AB的垂直平分线时,他是这样操作的:分别以点A和B为圆心,大于的长为半径画弧,两弧交于点C,D,则直线CD即为所求.根据他的作图方法可知四边形ADBC一定是 .(填“矩形”“菱形”或“正方形”)
【答案】菱形
9.如图,在 ABCD中,AC平分∠DAB,AB=3,则 ABCD的周长为 .
【答案】12
10.如图,在矩形ABCD中,AB=1,BG,DH分别平分∠ABC,∠ADC,交AD,BC于点G,H.要使四边形BHDG为菱形,则AD的长为 .
【答案】1+
11.如图,A,B两点的坐标分别为(5,0),(1,3),C是平面直角坐标系内一点.若以O,A,B,C四点为顶点的四边形是菱形,则点C的坐标为 .
【答案】(-4,3)
12.在平面直角坐标系中,已知点A(0,0),B(6,0),点C在第一象限,且AC=BC=6.若存在点D,使得以A,B,C,D为顶点的四边形是菱形,则点D的坐标为_________________________________.
【答案】(9,3)
三、解答题
13.如图,在四边形ABCD中,AD∥BC,对角线BD的垂直平分线与边AD,BC分别相交于点M,N.求证:四边形BNDM是菱形.
证明:∵AD∥BC,∴∠DMO=∠BNO.
由题可知OB=OD,MN⊥BD.
易证△MOD≌△NOB,∴OM=ON,
∴四边形BNDM是平行四边形.
∵MN⊥BD,∴平行四边形BNDM是菱形.
14.如图,在△ABC中,BC=2AB,D,E分别是边BC,AC的中点.将△CDE绕点E旋转180°得到△AFE.试判断四边形ABDF的形状,并证明.
解:四边形ABDF是菱形.
证明:由旋转的性质知EF=DE,AF=CD.
∵D,E分别是BC,AC的中点,
∴BD=CD,AB=2DE=DF.
∵BC=2AB,∴BD=DF=AF=AB,
∴四边形ABDF是菱形.
15.如图,在四边形ABCD中,∠ABC=∠DCB,四边形ABFD是平行四边形,DF交BC于点E,连接AE,CF,CF=BF.
(1)求证:△ADE≌△FCD.
(2)连接DB交AE于点G,连接CG,若AG=DC.求证:四边形BFCG是菱形.
证明:(1)证明略.
(2)由(1)知∠AED=∠FDC,∴AG∥DC.
∵AG=DC,∴四边形AGCD是平行四边形,
∴CG∥DA,CG=DA.
∵BF∥DA,BF=DA,∴CG∥BF,CG=BF,
∴四边形BFCG是平行四边形.
∵CF=BF,∴四边形BFCG是菱形.
16.如图1,△ABC为等腰三角形,AB=AC=a,P是底边BC上的一个动点,PD∥AC,PE∥AB.
(1)四边形ADPE的周长为 .(用含a的式子表示)
(2)当点P运动到什么位置时,四边形ADPE是菱形?请说明理由.
(3)如果△ABC不是等腰三角形,如图2,其他条件不变,当点P运动到什么位置时,四边形ADPE是菱形?(不必说明理由)
图1 图2
解:(1)2a
(2)当点P运动到BC的中点时,四边形ADPE是菱形.
理由略.
(3)点P运动到∠BAC的平分线上时,四边形ADPE是菱形.
17.如图,将一张矩形纸片ABCD沿着对角线BD向上折叠,顶点C落到点E处,BE交AD于点F.
(1)求证:△BDF是等腰三角形;
(2)如图2,过点D作DG∥BE,交BC于点G,连接FG交BD于点O.
①判断四边形BFDG的形状,并说明理由;
②若AB=6,AD=8,求FG的长.
(1)证明:根据折叠,∠DBC=∠DBE, 又AD∥BC,∴∠DBC=∠ADB,∴∠DBE=∠ADB,∴DF=BF,∴△BDF是等腰三角形;
(2)解:①∵四边形ABCD是矩形,∴AD∥BC,∴FD∥BG,又∵FB∥DG,∴四边形BFDG是平行四边形,∵DF=BF,∴四边形BFDG是菱形; ②∵AB=6,AD=8,∴BD=10,∴OB=BD=5.假设DF=BF=x,∴AF=AD-DF=8-x.∴在直角△ABF中,AB2+AF2=BF2,即62+(8-x)2=x2,解得x=,即BF=,∴FO===,∴FG=2FO=.
18.2.2 菱形
第2课时 菱形的判定
一、选择题
1.下列条件中,能判定四边形是菱形的是( )
A.两条对角线相等 B.两条对角线互相垂直
C.两条对角线互相垂直平分 D.两条对角线互相平分且相等
2.在平行四边形ABCD中添加下列条件,不能判定四边形ABCD是菱形的是( )
A.AB=BC B.AC⊥BD C.AC=BD D.∠ABD=∠CBD
3.在数学活动课上,为探究四边形瓷砖是否为菱形,以下拟定的测量方案,正确的是( )
A.测量一组对边是否平行且相等 B.测量四个内角是否相等
C.测量两条对角线是否互相垂直 D.测量四条边是否相等
4.用直尺和圆规作一个以线段AB为边的菱形,作图痕迹如图所示,能得到四边形ABCD是菱形的依据是( )
A.一组邻边相等的四边形是菱形 B.四边相等的四边形是菱形
C.对角线互相垂直的平行四边形是菱形
D.每条对角线平分一组对角的平行四边形是菱形
5.如图,在四边形ABCD中,E、F、G、H分别是AB、BD、CD、AC的中点,要使四边形EFGH是菱形,则四边形ABCD只需要满足一个条件,是( )
A.AD=BC B.AC=BD C.AB=CD D.AD=CD
6.如图,在△ABC中,D是BC边的中点,点E,F分别在线段AD及其延长线上,DE=DF.在下列条件中,使四边形BECF是菱形的是( )
A.EB⊥EC B.AB⊥AC C.AB=AC D.BF∥CE
二、填空题
7.如图,四边形ABCD是对角线互相垂直的四边形,且OB=OD.请你添加一个适当的条件 ,使四边形ABCD成为菱形.
8.如图,聪聪在作线段AB的垂直平分线时,他是这样操作的:分别以点A和B为圆心,大于的长为半径画弧,两弧交于点C,D,则直线CD即为所求.根据他的作图方法可知四边形ADBC一定是 .(填“矩形”“菱形”或“正方形”)
9.如图,在 ABCD中,AC平分∠DAB,AB=3,则 ABCD的周长为 .
10.如图,在矩形ABCD中,AB=1,BG,DH分别平分∠ABC,∠ADC,交AD,BC于点G,H.要使四边形BHDG为菱形,则AD的长为 .
11.如图,A,B两点的坐标分别为(5,0),(1,3),C是平面直角坐标系内一点.若以O,A,B,C四点为顶点的四边形是菱形,则点C的坐标为 .
12.在平面直角坐标系中,已知点A(0,0),B(6,0),点C在第一象限,且AC=BC=6.若存在点D,使得以A,B,C,D为顶点的四边形是菱形,则点D的坐标为_________________________________.
三、解答题
13.如图,在四边形ABCD中,AD∥BC,对角线BD的垂直平分线与边AD,BC分别相交于点M,N.求证:四边形BNDM是菱形.
14.如图,在△ABC中,BC=2AB,D,E分别是边BC,AC的中点.将△CDE绕点E旋转180°得到△AFE.试判断四边形ABDF的形状,并证明.
15.如图,在四边形ABCD中,∠ABC=∠DCB,四边形ABFD是平行四边形,DF交BC于点E,连接AE,CF,CF=BF.
(1)求证:△ADE≌△FCD.
(2)连接DB交AE于点G,连接CG,若AG=DC.求证:四边形BFCG是菱形.
16.如图1,△ABC为等腰三角形,AB=AC=a,P是底边BC上的一个动点,PD∥AC,PE∥AB.
(1)四边形ADPE的周长为 .(用含a的式子表示)
(2)当点P运动到什么位置时,四边形ADPE是菱形?请说明理由.
(3)如果△ABC不是等腰三角形,如图2,其他条件不变,当点P运动到什么位置时,四边形ADPE是菱形?(不必说明理由)
图1 图2
17.如图,将一张矩形纸片ABCD沿着对角线BD向上折叠,顶点C落到点E处,BE交AD于点F.
(1)求证:△BDF是等腰三角形;
(2)如图2,过点D作DG∥BE,交BC于点G,连接FG交BD于点O.
①判断四边形BFDG的形状,并说明理由;
②若AB=6,AD=8,求FG的长.
1
参考答案
一、选择题
1.下列条件中,能判定四边形是菱形的是( C )
A.两条对角线相等 B.两条对角线互相垂直
C.两条对角线互相垂直平分 D.两条对角线互相平分且相等
2.在平行四边形ABCD中添加下列条件,不能判定四边形ABCD是菱形的是( C )
A.AB=BC B.AC⊥BD C.AC=BD D.∠ABD=∠CBD
3.在数学活动课上,为探究四边形瓷砖是否为菱形,以下拟定的测量方案,正确的是( D )
A.测量一组对边是否平行且相等 B.测量四个内角是否相等
C.测量两条对角线是否互相垂直 D.测量四条边是否相等
4.用直尺和圆规作一个以线段AB为边的菱形,作图痕迹如图所示,能得到四边形ABCD是菱形的依据是( B )
A.一组邻边相等的四边形是菱形 B.四边相等的四边形是菱形
C.对角线互相垂直的平行四边形是菱形
D.每条对角线平分一组对角的平行四边形是菱形
5.如图,在四边形ABCD中,E、F、G、H分别是AB、BD、CD、AC的中点,要使四边形EFGH是菱形,则四边形ABCD只需要满足一个条件,是( A )
A.AD=BC B.AC=BD C.AB=CD D.AD=CD
6.如图,在△ABC中,D是BC边的中点,点E,F分别在线段AD及其延长线上,DE=DF.在下列条件中,使四边形BECF是菱形的是( C )
A.EB⊥EC B.AB⊥AC C.AB=AC D.BF∥CE
二、填空题
7.如图,四边形ABCD是对角线互相垂直的四边形,且OB=OD.请你添加一个适当的条件 ,使四边形ABCD成为菱形.
【答案】 OA=OC(答案不唯一,合理即可)
8.如图,聪聪在作线段AB的垂直平分线时,他是这样操作的:分别以点A和B为圆心,大于的长为半径画弧,两弧交于点C,D,则直线CD即为所求.根据他的作图方法可知四边形ADBC一定是 .(填“矩形”“菱形”或“正方形”)
【答案】菱形
9.如图,在 ABCD中,AC平分∠DAB,AB=3,则 ABCD的周长为 .
【答案】12
10.如图,在矩形ABCD中,AB=1,BG,DH分别平分∠ABC,∠ADC,交AD,BC于点G,H.要使四边形BHDG为菱形,则AD的长为 .
【答案】1+
11.如图,A,B两点的坐标分别为(5,0),(1,3),C是平面直角坐标系内一点.若以O,A,B,C四点为顶点的四边形是菱形,则点C的坐标为 .
【答案】(-4,3)
12.在平面直角坐标系中,已知点A(0,0),B(6,0),点C在第一象限,且AC=BC=6.若存在点D,使得以A,B,C,D为顶点的四边形是菱形,则点D的坐标为_________________________________.
【答案】(9,3)
三、解答题
13.如图,在四边形ABCD中,AD∥BC,对角线BD的垂直平分线与边AD,BC分别相交于点M,N.求证:四边形BNDM是菱形.
证明:∵AD∥BC,∴∠DMO=∠BNO.
由题可知OB=OD,MN⊥BD.
易证△MOD≌△NOB,∴OM=ON,
∴四边形BNDM是平行四边形.
∵MN⊥BD,∴平行四边形BNDM是菱形.
14.如图,在△ABC中,BC=2AB,D,E分别是边BC,AC的中点.将△CDE绕点E旋转180°得到△AFE.试判断四边形ABDF的形状,并证明.
解:四边形ABDF是菱形.
证明:由旋转的性质知EF=DE,AF=CD.
∵D,E分别是BC,AC的中点,
∴BD=CD,AB=2DE=DF.
∵BC=2AB,∴BD=DF=AF=AB,
∴四边形ABDF是菱形.
15.如图,在四边形ABCD中,∠ABC=∠DCB,四边形ABFD是平行四边形,DF交BC于点E,连接AE,CF,CF=BF.
(1)求证:△ADE≌△FCD.
(2)连接DB交AE于点G,连接CG,若AG=DC.求证:四边形BFCG是菱形.
证明:(1)证明略.
(2)由(1)知∠AED=∠FDC,∴AG∥DC.
∵AG=DC,∴四边形AGCD是平行四边形,
∴CG∥DA,CG=DA.
∵BF∥DA,BF=DA,∴CG∥BF,CG=BF,
∴四边形BFCG是平行四边形.
∵CF=BF,∴四边形BFCG是菱形.
16.如图1,△ABC为等腰三角形,AB=AC=a,P是底边BC上的一个动点,PD∥AC,PE∥AB.
(1)四边形ADPE的周长为 .(用含a的式子表示)
(2)当点P运动到什么位置时,四边形ADPE是菱形?请说明理由.
(3)如果△ABC不是等腰三角形,如图2,其他条件不变,当点P运动到什么位置时,四边形ADPE是菱形?(不必说明理由)
图1 图2
解:(1)2a
(2)当点P运动到BC的中点时,四边形ADPE是菱形.
理由略.
(3)点P运动到∠BAC的平分线上时,四边形ADPE是菱形.
17.如图,将一张矩形纸片ABCD沿着对角线BD向上折叠,顶点C落到点E处,BE交AD于点F.
(1)求证:△BDF是等腰三角形;
(2)如图2,过点D作DG∥BE,交BC于点G,连接FG交BD于点O.
①判断四边形BFDG的形状,并说明理由;
②若AB=6,AD=8,求FG的长.
(1)证明:根据折叠,∠DBC=∠DBE, 又AD∥BC,∴∠DBC=∠ADB,∴∠DBE=∠ADB,∴DF=BF,∴△BDF是等腰三角形;
(2)解:①∵四边形ABCD是矩形,∴AD∥BC,∴FD∥BG,又∵FB∥DG,∴四边形BFDG是平行四边形,∵DF=BF,∴四边形BFDG是菱形; ②∵AB=6,AD=8,∴BD=10,∴OB=BD=5.假设DF=BF=x,∴AF=AD-DF=8-x.∴在直角△ABF中,AB2+AF2=BF2,即62+(8-x)2=x2,解得x=,即BF=,∴FO===,∴FG=2FO=.
