第2单元比例易错精选题(同步练习) 六年级下册数学北师大版(含解析)
文档属性
| 名称 | 第2单元比例易错精选题(同步练习) 六年级下册数学北师大版(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 167.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-31 10:56:51 | ||
图片预览




文档简介
第2单元比例易错精选题-数学六年级下册北师大版
一、选择题
1.用10、1.5、8、1.2四个数组成比例,下面( )是不正确的。
A.10∶8=1.5∶1.2 B.8∶1.5=10∶1.2
C.8∶10=1.2∶1.5 D.1.5∶1.2=10∶8
2.图上5cm表示实际200km,这幅图的比例尺是( )。
A.1∶4000 B.1∶40000 C.1∶400000 D.1∶4000000
3.淘气调制了一杯糖水,糖和水的质量比是2∶25。其中糖用了12g,共调制糖水( )g。
A.25 B.150 C.162 D.250
4.一个零件长3cm,把它画在比例尺是10∶1的图纸上,长应画( )cm。
A.0.3 B.3 C.30 D.300
5.已知一个圆的半径是R,且R满足3∶R=R∶4,则这个圆的面积为( )。
A.7π B.7 C.12π D.无法求出
6.在比例尺为1∶3000000的地图上,量得A、B两个港口的距离为9厘米。一艘轮船于上午8时以每小时27千米的速度从港口A出发,到达港口B的时间为( )。
A.17时 B.18时 C.19时 D.20时
二、填空题
7.6个矿泉水空瓶可以换2包糖,我用21个矿泉水空瓶换了x包糖。请根据题意,写出比例( )。
8.在比例中,两个外项互为倒数,其中一个内项是0.75,则另一个内项是( )。
9.把等式改写成一个比例是( )。
10.在比例尺是1∶5000000的地图上,量得两城市之间的距离是6.4厘米。这两座城市之间的实际距离是( )千米。
11.某个零件的长为12毫米,画在图上,比例尺为10∶1,图上应该画( )。
12.一个长3分米、宽2分米的长方形按3∶1放大,得到的图形面积是( )平方分米,周长是( )分米。
三、判断题
13.一个正方形按4∶1放大,它的周长和面积都是原来的4倍。( )
14.从甲地到乙地,A车用了6小时,B车用了8小时,A、B两车的速度比是3∶4。( )
15.能与∶0.2组成比例的比有无数个。( )
16.一个机器零件长4毫米,画在图纸上长8厘米,这幅图的比例尺是2∶1。( )
17.甲数的等于乙数的(甲数、乙数不为0),那么甲数与乙数的比是15∶8。( )
四、计算题
18.解比例。
x∶12=∶2.8 100∶x=60∶25% =
五、解答题
19.学校把制作爱心贺卡的任务按5∶4分配给六年级和五年级,五年级实际制作了120个,超过原分配任务的20%,原计划六年级制作多少个爱心贺卡?
20.甲、乙两城之间的航空线在比例尺为1∶6000000地图上长15厘米,一架民航机从甲城飞往乙城的时速是750千米,飞行30分钟后离乙城还有多远?
21.甲、乙两箱苹果共重60千克,取出甲箱苹果的放入乙箱后,甲箱苹果与乙箱苹果的重量之比为2∶3,甲、乙两箱苹果原来各有多少千克?
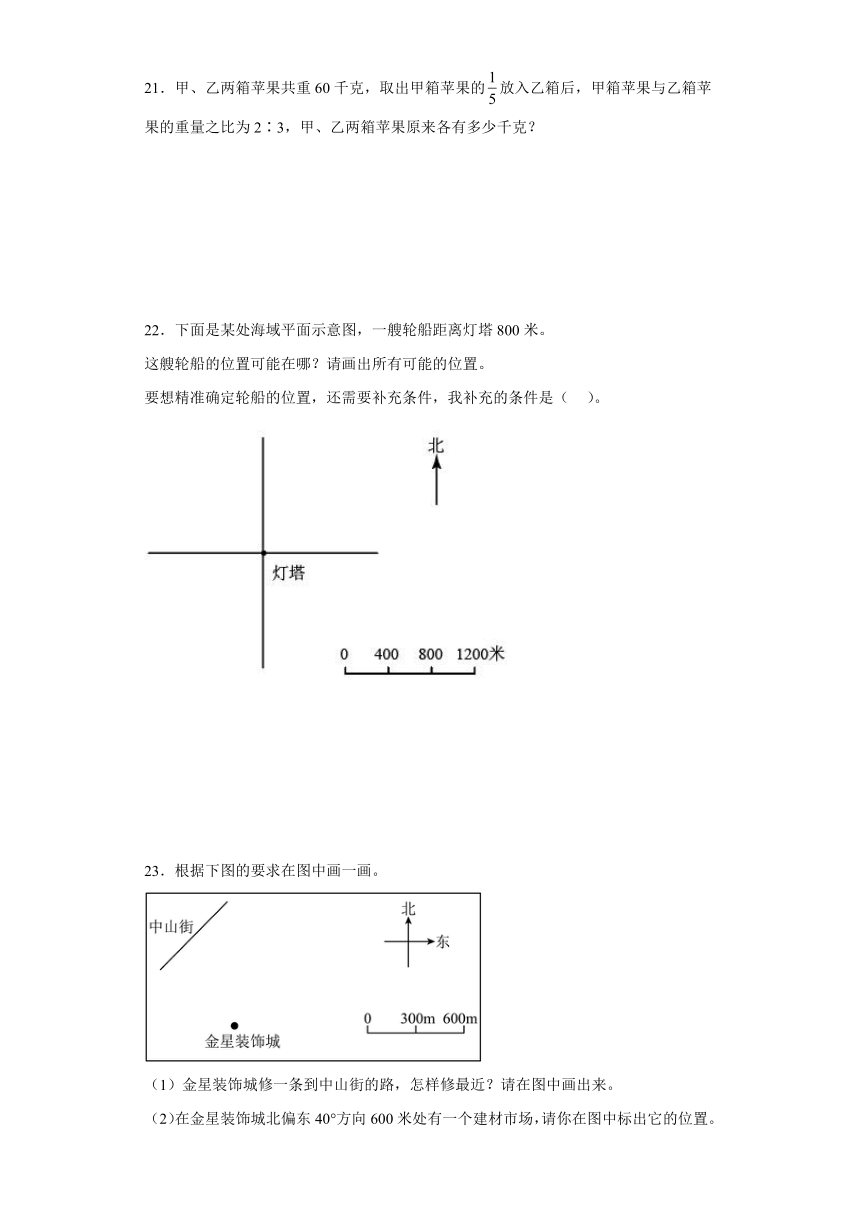
22.下面是某处海域平面示意图,一艘轮船距离灯塔800米。
这艘轮船的位置可能在哪?请画出所有可能的位置。
要想精准确定轮船的位置,还需要补充条件,我补充的条件是( )。
23.根据下图的要求在图中画一画。
(1)金星装饰城修一条到中山街的路,怎样修最近?请在图中画出来。
(2)在金星装饰城北偏东40°方向600米处有一个建材市场,请你在图中标出它的位置。
参考答案:
1.B
【解析】比例的基本性质:在比例中,两个外项的积等于两个内项的积,据此解答。
【详解】A.10∶8=1.5∶1.2,10×1.2=12,8×1.5=12,成比例;
B.8∶1.5=10∶1.2,8×1.2=9.6,1.5×10=15,8×1.2≠1.5×10,不成比例;
C.8∶10=1.2∶1.5,8×1.5=12,10×1.2=12,成比例。
D.1.5∶1.2=10∶8,1.5×8=12,1.2×10=12,成比例。
故答案为:B
【点睛】外项的积等于内项的积,就成比例;外项的积不等于内项的积,就不成比例。
2.D
【解析】一幅图的图上距离和实际距离的比,叫做这幅图的比例尺。
【详解】200km=20000000cm
5∶20000000=1∶4000000
故答案为:D
【点睛】考查了比例尺,注意图上距离和实际距离单位要统一。
3.C
【解析】糖与水的比是2∶25,也就是水是糖的倍,用乘法求出水用了多少,再加上糖的量即可求出糖水的量。
【详解】12×+12
=150+12
=162(g)
故答案为:C
【点睛】本题考查了按比例分配,解题的关键是根据糖与水的比,求出水的克数。
4.C
【解析】图上距离=实际距离×比例尺,据此解答。
【详解】3×10=30(cm)
故答案为:C
【点睛】考查了图上距离和实际距离的换算,根据公式代入数据即可得出答案。
5.C
【分析】根据比例的基本性质:两个内项的乘积等于两个外项的乘积和圆的面积=π×半径×半径即可求解。
【详解】由3∶R=R∶4可转化为乘积的形式:R×R=3×4,即半径×半径=12。即圆的面积=π×半径×半径=12π。
故答案为:C
【点睛】灵活运用比例的基本性质和圆的面积公式的是解题的关键。
6.B
【分析】根据实际距离=图上距离÷比例尺,据此求出A、B两个港口的实际距离,再除以速度即可求出行驶时间,结束时间=开始时间+经过时间,据此解答。
【详解】9÷ =27000000(厘米)=270(千米)
270÷27=10(时)
8+10=18(时)
故选择:B
【点睛】此题主要考查了比例尺的实际应用,先求出两地的实际距离是解题关键。
7.6∶2=21∶x
【分析】根据比例的意义:表示两个比相等的式子叫做比例;用6个矿泉水空瓶可以换2包糖,所以每包糖的可以换(6÷2)瓶矿泉水瓶,用比表示就是6∶2;用21个矿泉水空瓶可以换x包糖,所以每包糖的可以换(21÷x)瓶矿泉水空瓶,用比表示就是21∶x;两个比的比值相等,据此写出比例(答案不唯一)。
【详解】根据分析可知,6个矿泉水空瓶可以换2包糖,我用21个矿泉水空瓶换了x包糖。请根据题意,写出比例:6∶2=21∶x。
【点睛】熟练掌握比例的意义并能灵活运用。
8.
【分析】根据比例的性质:两个内项之积等于两个外项之积;倒数的意义:乘积是1的两个数互为倒数,两个外项之积互为倒数,即两个外项之积等于1,则两个内项之积等于1,用1÷一个内项,即可求出另一个内项。
【详解】1÷0.75
=1÷
=1×
=
【点睛】利用比例的基本性质、倒数的意义进行解答。
9.2.5∶0.5=4∶0.8(答案不唯一)
【分析】在比例里,两个外项的积等于两个内项的积,这叫做比例的基本性质,根据比例的基本性质的逆用,写出比例式即可。
【详解】因为2.5×0.8=0.5×4
所以2.5∶0.5=4∶0.8(答案不唯一)
【点睛】熟练掌握比例的基本性质的逆是解题的关键。
10.320
【分析】要求两座城市之间的实际距离是多少千米,根据“图上距离÷比例尺=实际距离”,代入数值计算即可。
【详解】6.4÷=32000000(厘米)
32000000厘米=320千米
【点睛】本意主要考查比例尺的实际应用。
11.12厘米
【分析】图上距离=实际距离×比例尺,代入数据解答即可。
【详解】12毫米=1.2厘米
1.2×10=12厘米
【点睛】解答此题的关键是掌握比例尺的相关公式。
12. 54 30
【分析】根据图形放大与缩小的意义,一个长3分米、宽2分米的长方形按3∶1放大后,长、宽都扩大到原来的3倍,放大后的长方形的长、宽都分别是9分米、6分米;根据长方形的面积公式S=ab即可求出面积;根据长方形的周长公式C=2(a+b)即可求出周长。
【详解】(3×3)×(2×3)
=9×6
=54(平方分米)
2×(3×3+2×3)
=2×(9+6)
=2×15
=30(分米)
【点睛】本题是考查图形的放大与缩小、长方形的面积与周长的计算。
13.×
【分析】根据正方形的边长比=周长比,边长平方以后的比=面积比,进行分析。
【详解】42∶12=16∶1,一个正方形按4∶1放大后,周长扩大到原来的4倍,面积扩大到原来的16倍,所以原题说法错误。
故答案为:×
【点睛】本题考查了图形的放大与缩小,图形放大或缩小后,对应边长的比相等,周长的比相等,但面积的比不相等。
14.×
【分析】将两地的距离看成单位“1”,根据A车和B车分别用的时间,先分别求出两车的速度,写出比并化简即可。
【详解】1÷6=
1÷8=
∶=4∶3,即A、B两车的速度比是4∶3。
故答案为:×
【点睛】此题关键是先求出两车的速度,进而写比并化简比。
15.√
【分析】表示两个比相等的式子就是比例,只要与∶0.2的比值相等的比就可以与∶0.2组成比例,这样的比有无数个,所以能与∶0.2组成比例的比也有无数个,据此判断。
【详解】由分析可知,能与∶0.2组成比例的比有无数个,说法正确。
故答案为:√
【点睛】此题考查了比例的意义,明确只要两个比的比值相等,就能组成比例。
16.×
【分析】根据比例尺=图上距离∶实际距离,把数代入并化简即可(要注意先统一单位)。
【详解】8厘米=80毫米
比例尺=80毫米∶4毫米=20∶1
故答案为:×。
【点睛】本题主要考查比例尺的意义,熟练掌握比例尺的意义并灵活运用。
17.√
【分析】由题意可知:甲数×=乙数×,于是逆运用比例的基本性质,即可求出两个数的比。
【详解】因为甲数×=乙数×,则甲数∶乙数=∶=15∶8。
故答案为:√
【点睛】此题主要考查比例的基本性质的灵活应用。
18.x=7.5;x=;x=2
【分析】x∶12=∶2.8,解比例,原式化为:2.8x=12×,再根据等式的性质2,方程两边同时除以2.8即可;
100∶x=60∶25%,解比例,原式化为:60x=100×25%,再根据等式的性质2,方程两边同时除以60即可;
=,解比例,原式化为:9x=4×4.5,再根据等式的性质2,方程两边同时除以9即可。
【详解】x∶12=∶2.8
解:2.8x=12×
2.8x=21
x=21÷2.8
x=7.5
100∶x=60∶25%
解:60x=100×25%
60x=25
x=25÷60
x=
=
解:9x=4×4.5
9x=18
x=18÷9
x=2
19.125个
【分析】根据题意,五年级实际制作了120个,超出原分配任务的20%,求出五年级原计划制作的爱心卡片,把五年级原计划制作的爱心卡片总数看作单位“1”,超出20%,实际制作了1+20%,用120÷(1+20%),求出五年级原计划制作爱心卡片,设六年级原计划制作x个爱心卡片,根据比例的基本性质,内项之积等于外项之积,六年级制作爱心卡片∶五年级制作爱心卡片=5∶4,列方程:x∶[120÷(1+20%)]=5∶4,解比例,即可解答。
【详解】解:设六年级原计划制作爱心卡片x个。
x∶[120÷(1+20%)]=5∶4
x∶[120÷1.2]=5∶4
x∶100=5∶4
4x=5×100
4x=500
x=500÷5
x=125
答:原计划六年级制作125个爱心卡片。
【点睛】本题考查方程的实际应用,根据比例的基本性质,列方程,解比例。
20.525千米
【分析】此题应先求出甲、乙两地的实际距离(即全程),根据实际距离=图上距离÷比例尺可求出,然后用全程减民航机30分钟飞行的航程,即为离乙城的距离。
【详解】甲、乙两城之间的实际距离:
15÷=90000000厘米=900(千米)
30分钟=0.5小时
30分钟后离乙城的距离:
900-750×0.5
=900-375
=525(千米)
答:飞行30分钟后离乙城还有525千米。
【点睛】此题考查了比例尺的实际应用,以及对“时间×速度=路程”这一关系式的理解掌握。
21.30千克;30千克
【分析】由甲、乙两箱苹果共重60千克,设甲箱苹果重x千克,则乙箱苹果重(60-x)千克;甲箱苹果取出放入乙箱后,还剩甲箱苹果的(1-),根据甲箱苹果与乙箱苹果的重量比为2∶3,可列方程:(x-x)∶(60-x+x)=2∶3。解方程求解即可。
【详解】解:设甲箱苹果重x千克,则乙箱苹果重(60-x)千克。
(x-x)∶(60-x+x)=2∶3
x∶(60-x)=2∶3
x=120-x
4x=120
x=30
乙:60-30=30(千克)
答:甲箱苹果原来有30千克,乙箱苹果有30千克。
【点睛】本题主要考查列方程解决含有两个未知量的实际问题,解答的关键在于找出等量关系。
22.图见详解;轮船在灯塔东偏北30°方向,距离800米。(答案不唯一)
【分析】(1)根据题意可知,这艘轮船的位置是以灯塔为圆心,实际距离800米为半径的圆上,据此画图;
(2)根据方向和距离方可确定物体的位置,现在只知道距离,所以知道了方向就知道轮船的具体位置了,据此解答。
【详解】图上1厘米表示实际距离400米,所以实际距离800米,图上距离是2厘米。
要想精准确定轮船的位置,还需要补充条件,我补充的条件是:轮船在灯塔东偏北30°方向,距离800米。(答案不唯一)
【点睛】在确定了观测点后,确定另一个物体的位置,要有两个要素:方向、距离。
23.见解析
【分析】(1)根据“点到直线的距离垂线段最短”可知从金星装饰城修一条垂直于中山街的路最近;
(2)根据图“上北、下南、左西、右东”,以及比例尺,用600除以图上1厘米代表的实际距离300米,求出金星装饰到建材商场的图上长度是多少,然后画出建材市场的位置即可。
【详解】(1)从金星装饰城修一条垂直于中山街的路最近(如图)
(2)600÷300=2(厘米)
所以图上建材市场位于金星装饰城北偏东方向2厘米处(如图)
【点睛】此题主要考查线段比例尺的意义,以及依据方向和距离确定物体位置的方法。
一、选择题
1.用10、1.5、8、1.2四个数组成比例,下面( )是不正确的。
A.10∶8=1.5∶1.2 B.8∶1.5=10∶1.2
C.8∶10=1.2∶1.5 D.1.5∶1.2=10∶8
2.图上5cm表示实际200km,这幅图的比例尺是( )。
A.1∶4000 B.1∶40000 C.1∶400000 D.1∶4000000
3.淘气调制了一杯糖水,糖和水的质量比是2∶25。其中糖用了12g,共调制糖水( )g。
A.25 B.150 C.162 D.250
4.一个零件长3cm,把它画在比例尺是10∶1的图纸上,长应画( )cm。
A.0.3 B.3 C.30 D.300
5.已知一个圆的半径是R,且R满足3∶R=R∶4,则这个圆的面积为( )。
A.7π B.7 C.12π D.无法求出
6.在比例尺为1∶3000000的地图上,量得A、B两个港口的距离为9厘米。一艘轮船于上午8时以每小时27千米的速度从港口A出发,到达港口B的时间为( )。
A.17时 B.18时 C.19时 D.20时
二、填空题
7.6个矿泉水空瓶可以换2包糖,我用21个矿泉水空瓶换了x包糖。请根据题意,写出比例( )。
8.在比例中,两个外项互为倒数,其中一个内项是0.75,则另一个内项是( )。
9.把等式改写成一个比例是( )。
10.在比例尺是1∶5000000的地图上,量得两城市之间的距离是6.4厘米。这两座城市之间的实际距离是( )千米。
11.某个零件的长为12毫米,画在图上,比例尺为10∶1,图上应该画( )。
12.一个长3分米、宽2分米的长方形按3∶1放大,得到的图形面积是( )平方分米,周长是( )分米。
三、判断题
13.一个正方形按4∶1放大,它的周长和面积都是原来的4倍。( )
14.从甲地到乙地,A车用了6小时,B车用了8小时,A、B两车的速度比是3∶4。( )
15.能与∶0.2组成比例的比有无数个。( )
16.一个机器零件长4毫米,画在图纸上长8厘米,这幅图的比例尺是2∶1。( )
17.甲数的等于乙数的(甲数、乙数不为0),那么甲数与乙数的比是15∶8。( )
四、计算题
18.解比例。
x∶12=∶2.8 100∶x=60∶25% =
五、解答题
19.学校把制作爱心贺卡的任务按5∶4分配给六年级和五年级,五年级实际制作了120个,超过原分配任务的20%,原计划六年级制作多少个爱心贺卡?
20.甲、乙两城之间的航空线在比例尺为1∶6000000地图上长15厘米,一架民航机从甲城飞往乙城的时速是750千米,飞行30分钟后离乙城还有多远?
21.甲、乙两箱苹果共重60千克,取出甲箱苹果的放入乙箱后,甲箱苹果与乙箱苹果的重量之比为2∶3,甲、乙两箱苹果原来各有多少千克?
22.下面是某处海域平面示意图,一艘轮船距离灯塔800米。
这艘轮船的位置可能在哪?请画出所有可能的位置。
要想精准确定轮船的位置,还需要补充条件,我补充的条件是( )。
23.根据下图的要求在图中画一画。
(1)金星装饰城修一条到中山街的路,怎样修最近?请在图中画出来。
(2)在金星装饰城北偏东40°方向600米处有一个建材市场,请你在图中标出它的位置。
参考答案:
1.B
【解析】比例的基本性质:在比例中,两个外项的积等于两个内项的积,据此解答。
【详解】A.10∶8=1.5∶1.2,10×1.2=12,8×1.5=12,成比例;
B.8∶1.5=10∶1.2,8×1.2=9.6,1.5×10=15,8×1.2≠1.5×10,不成比例;
C.8∶10=1.2∶1.5,8×1.5=12,10×1.2=12,成比例。
D.1.5∶1.2=10∶8,1.5×8=12,1.2×10=12,成比例。
故答案为:B
【点睛】外项的积等于内项的积,就成比例;外项的积不等于内项的积,就不成比例。
2.D
【解析】一幅图的图上距离和实际距离的比,叫做这幅图的比例尺。
【详解】200km=20000000cm
5∶20000000=1∶4000000
故答案为:D
【点睛】考查了比例尺,注意图上距离和实际距离单位要统一。
3.C
【解析】糖与水的比是2∶25,也就是水是糖的倍,用乘法求出水用了多少,再加上糖的量即可求出糖水的量。
【详解】12×+12
=150+12
=162(g)
故答案为:C
【点睛】本题考查了按比例分配,解题的关键是根据糖与水的比,求出水的克数。
4.C
【解析】图上距离=实际距离×比例尺,据此解答。
【详解】3×10=30(cm)
故答案为:C
【点睛】考查了图上距离和实际距离的换算,根据公式代入数据即可得出答案。
5.C
【分析】根据比例的基本性质:两个内项的乘积等于两个外项的乘积和圆的面积=π×半径×半径即可求解。
【详解】由3∶R=R∶4可转化为乘积的形式:R×R=3×4,即半径×半径=12。即圆的面积=π×半径×半径=12π。
故答案为:C
【点睛】灵活运用比例的基本性质和圆的面积公式的是解题的关键。
6.B
【分析】根据实际距离=图上距离÷比例尺,据此求出A、B两个港口的实际距离,再除以速度即可求出行驶时间,结束时间=开始时间+经过时间,据此解答。
【详解】9÷ =27000000(厘米)=270(千米)
270÷27=10(时)
8+10=18(时)
故选择:B
【点睛】此题主要考查了比例尺的实际应用,先求出两地的实际距离是解题关键。
7.6∶2=21∶x
【分析】根据比例的意义:表示两个比相等的式子叫做比例;用6个矿泉水空瓶可以换2包糖,所以每包糖的可以换(6÷2)瓶矿泉水瓶,用比表示就是6∶2;用21个矿泉水空瓶可以换x包糖,所以每包糖的可以换(21÷x)瓶矿泉水空瓶,用比表示就是21∶x;两个比的比值相等,据此写出比例(答案不唯一)。
【详解】根据分析可知,6个矿泉水空瓶可以换2包糖,我用21个矿泉水空瓶换了x包糖。请根据题意,写出比例:6∶2=21∶x。
【点睛】熟练掌握比例的意义并能灵活运用。
8.
【分析】根据比例的性质:两个内项之积等于两个外项之积;倒数的意义:乘积是1的两个数互为倒数,两个外项之积互为倒数,即两个外项之积等于1,则两个内项之积等于1,用1÷一个内项,即可求出另一个内项。
【详解】1÷0.75
=1÷
=1×
=
【点睛】利用比例的基本性质、倒数的意义进行解答。
9.2.5∶0.5=4∶0.8(答案不唯一)
【分析】在比例里,两个外项的积等于两个内项的积,这叫做比例的基本性质,根据比例的基本性质的逆用,写出比例式即可。
【详解】因为2.5×0.8=0.5×4
所以2.5∶0.5=4∶0.8(答案不唯一)
【点睛】熟练掌握比例的基本性质的逆是解题的关键。
10.320
【分析】要求两座城市之间的实际距离是多少千米,根据“图上距离÷比例尺=实际距离”,代入数值计算即可。
【详解】6.4÷=32000000(厘米)
32000000厘米=320千米
【点睛】本意主要考查比例尺的实际应用。
11.12厘米
【分析】图上距离=实际距离×比例尺,代入数据解答即可。
【详解】12毫米=1.2厘米
1.2×10=12厘米
【点睛】解答此题的关键是掌握比例尺的相关公式。
12. 54 30
【分析】根据图形放大与缩小的意义,一个长3分米、宽2分米的长方形按3∶1放大后,长、宽都扩大到原来的3倍,放大后的长方形的长、宽都分别是9分米、6分米;根据长方形的面积公式S=ab即可求出面积;根据长方形的周长公式C=2(a+b)即可求出周长。
【详解】(3×3)×(2×3)
=9×6
=54(平方分米)
2×(3×3+2×3)
=2×(9+6)
=2×15
=30(分米)
【点睛】本题是考查图形的放大与缩小、长方形的面积与周长的计算。
13.×
【分析】根据正方形的边长比=周长比,边长平方以后的比=面积比,进行分析。
【详解】42∶12=16∶1,一个正方形按4∶1放大后,周长扩大到原来的4倍,面积扩大到原来的16倍,所以原题说法错误。
故答案为:×
【点睛】本题考查了图形的放大与缩小,图形放大或缩小后,对应边长的比相等,周长的比相等,但面积的比不相等。
14.×
【分析】将两地的距离看成单位“1”,根据A车和B车分别用的时间,先分别求出两车的速度,写出比并化简即可。
【详解】1÷6=
1÷8=
∶=4∶3,即A、B两车的速度比是4∶3。
故答案为:×
【点睛】此题关键是先求出两车的速度,进而写比并化简比。
15.√
【分析】表示两个比相等的式子就是比例,只要与∶0.2的比值相等的比就可以与∶0.2组成比例,这样的比有无数个,所以能与∶0.2组成比例的比也有无数个,据此判断。
【详解】由分析可知,能与∶0.2组成比例的比有无数个,说法正确。
故答案为:√
【点睛】此题考查了比例的意义,明确只要两个比的比值相等,就能组成比例。
16.×
【分析】根据比例尺=图上距离∶实际距离,把数代入并化简即可(要注意先统一单位)。
【详解】8厘米=80毫米
比例尺=80毫米∶4毫米=20∶1
故答案为:×。
【点睛】本题主要考查比例尺的意义,熟练掌握比例尺的意义并灵活运用。
17.√
【分析】由题意可知:甲数×=乙数×,于是逆运用比例的基本性质,即可求出两个数的比。
【详解】因为甲数×=乙数×,则甲数∶乙数=∶=15∶8。
故答案为:√
【点睛】此题主要考查比例的基本性质的灵活应用。
18.x=7.5;x=;x=2
【分析】x∶12=∶2.8,解比例,原式化为:2.8x=12×,再根据等式的性质2,方程两边同时除以2.8即可;
100∶x=60∶25%,解比例,原式化为:60x=100×25%,再根据等式的性质2,方程两边同时除以60即可;
=,解比例,原式化为:9x=4×4.5,再根据等式的性质2,方程两边同时除以9即可。
【详解】x∶12=∶2.8
解:2.8x=12×
2.8x=21
x=21÷2.8
x=7.5
100∶x=60∶25%
解:60x=100×25%
60x=25
x=25÷60
x=
=
解:9x=4×4.5
9x=18
x=18÷9
x=2
19.125个
【分析】根据题意,五年级实际制作了120个,超出原分配任务的20%,求出五年级原计划制作的爱心卡片,把五年级原计划制作的爱心卡片总数看作单位“1”,超出20%,实际制作了1+20%,用120÷(1+20%),求出五年级原计划制作爱心卡片,设六年级原计划制作x个爱心卡片,根据比例的基本性质,内项之积等于外项之积,六年级制作爱心卡片∶五年级制作爱心卡片=5∶4,列方程:x∶[120÷(1+20%)]=5∶4,解比例,即可解答。
【详解】解:设六年级原计划制作爱心卡片x个。
x∶[120÷(1+20%)]=5∶4
x∶[120÷1.2]=5∶4
x∶100=5∶4
4x=5×100
4x=500
x=500÷5
x=125
答:原计划六年级制作125个爱心卡片。
【点睛】本题考查方程的实际应用,根据比例的基本性质,列方程,解比例。
20.525千米
【分析】此题应先求出甲、乙两地的实际距离(即全程),根据实际距离=图上距离÷比例尺可求出,然后用全程减民航机30分钟飞行的航程,即为离乙城的距离。
【详解】甲、乙两城之间的实际距离:
15÷=90000000厘米=900(千米)
30分钟=0.5小时
30分钟后离乙城的距离:
900-750×0.5
=900-375
=525(千米)
答:飞行30分钟后离乙城还有525千米。
【点睛】此题考查了比例尺的实际应用,以及对“时间×速度=路程”这一关系式的理解掌握。
21.30千克;30千克
【分析】由甲、乙两箱苹果共重60千克,设甲箱苹果重x千克,则乙箱苹果重(60-x)千克;甲箱苹果取出放入乙箱后,还剩甲箱苹果的(1-),根据甲箱苹果与乙箱苹果的重量比为2∶3,可列方程:(x-x)∶(60-x+x)=2∶3。解方程求解即可。
【详解】解:设甲箱苹果重x千克,则乙箱苹果重(60-x)千克。
(x-x)∶(60-x+x)=2∶3
x∶(60-x)=2∶3
x=120-x
4x=120
x=30
乙:60-30=30(千克)
答:甲箱苹果原来有30千克,乙箱苹果有30千克。
【点睛】本题主要考查列方程解决含有两个未知量的实际问题,解答的关键在于找出等量关系。
22.图见详解;轮船在灯塔东偏北30°方向,距离800米。(答案不唯一)
【分析】(1)根据题意可知,这艘轮船的位置是以灯塔为圆心,实际距离800米为半径的圆上,据此画图;
(2)根据方向和距离方可确定物体的位置,现在只知道距离,所以知道了方向就知道轮船的具体位置了,据此解答。
【详解】图上1厘米表示实际距离400米,所以实际距离800米,图上距离是2厘米。
要想精准确定轮船的位置,还需要补充条件,我补充的条件是:轮船在灯塔东偏北30°方向,距离800米。(答案不唯一)
【点睛】在确定了观测点后,确定另一个物体的位置,要有两个要素:方向、距离。
23.见解析
【分析】(1)根据“点到直线的距离垂线段最短”可知从金星装饰城修一条垂直于中山街的路最近;
(2)根据图“上北、下南、左西、右东”,以及比例尺,用600除以图上1厘米代表的实际距离300米,求出金星装饰到建材商场的图上长度是多少,然后画出建材市场的位置即可。
【详解】(1)从金星装饰城修一条垂直于中山街的路最近(如图)
(2)600÷300=2(厘米)
所以图上建材市场位于金星装饰城北偏东方向2厘米处(如图)
【点睛】此题主要考查线段比例尺的意义,以及依据方向和距离确定物体位置的方法。
