人教版八年级下册18.2.3.1 正方形的性质 同步练习(含答案)
文档属性
| 名称 | 人教版八年级下册18.2.3.1 正方形的性质 同步练习(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 272.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-31 11:56:50 | ||
图片预览


文档简介
第十八章 平行四边形
18.2.3 正方形
第1课时 正方形的性质
一、选择题
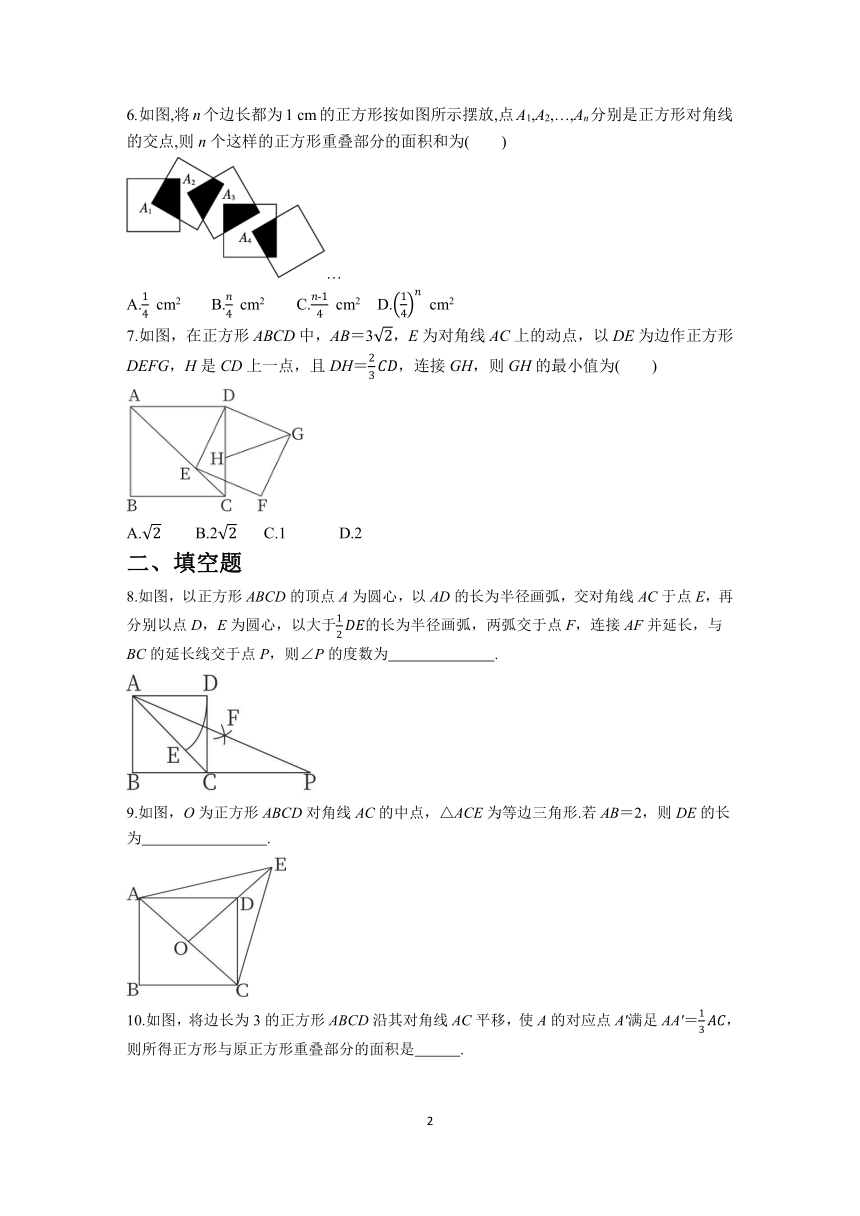
1.正方形具有而菱形不一定有的性质是( )
A.对角线互相垂直 B.对角线相等 C.对角相等 D.邻边相等
2.如图,P是正方形ABCD内位于对角线AC下方的一点,∠1=∠2,则∠BPC的度数为( )
A.135° B.130° C.125° D.120°
3.如图,四边形ABCD为正方形,点A的坐标为(-1,0),点B,C,D分别在坐标轴上,则正方形的周长是( )
A.4 B.3 C.4 D.2
4.如图,在正方形ABCD的外侧作等边△ABE,则∠BED的度数为( )
A.15° B.35° C.45° D.55°
5.如图,正方形ABCD的边长为8,M在DC上,且DM=2,N是AC上一动点,则DN+MN的最小值为( )
A.8 B.10 C.2 D.8
6.如图,将n个边长都为1 cm的正方形按如图所示摆放,点A1,A2,…,An分别是正方形对角线的交点,则n个这样的正方形重叠部分的面积和为( )
…
A. cm2 B. cm2 C. cm2 D. cm2
7.如图,在正方形ABCD中,AB=3,E为对角线AC上的动点,以DE为边作正方形DEFG,H是CD上一点,且DH=,连接GH,则GH的最小值为( )
A. B.2 C.1 D.2
二、填空题
8.如图,以正方形ABCD的顶点A为圆心,以AD的长为半径画弧,交对角线AC于点E,再分别以点D,E为圆心,以大于的长为半径画弧,两弧交于点F,连接AF并延长,与BC的延长线交于点P,则∠P的度数为 .
9.如图,O为正方形ABCD对角线AC的中点,△ACE为等边三角形.若AB=2,则DE的长为 .
10.如图,将边长为3的正方形ABCD沿其对角线AC平移,使A的对应点A'满足AA'=,则所得正方形与原正方形重叠部分的面积是 .
11.如图,正方形ABCD的边长为2,E为与点D不重合的动点,以DE为一边作正方形DEFG.设DE=d1,点F,G与点C的距离分别为d2,d3,则d1+d2+d3的最小值为 .
三、解答题
12.如图,在正方形ABCD中,点E,M,N分别在AB,BC,AD边上,CE=MN.求证:CE⊥MN.
13.如图,正方形ABCD,G是BC边上任意一点(不与B,C重合),DE⊥AG于点E,BF∥DE,且交AG于点F.求证:AF-BF=EF.
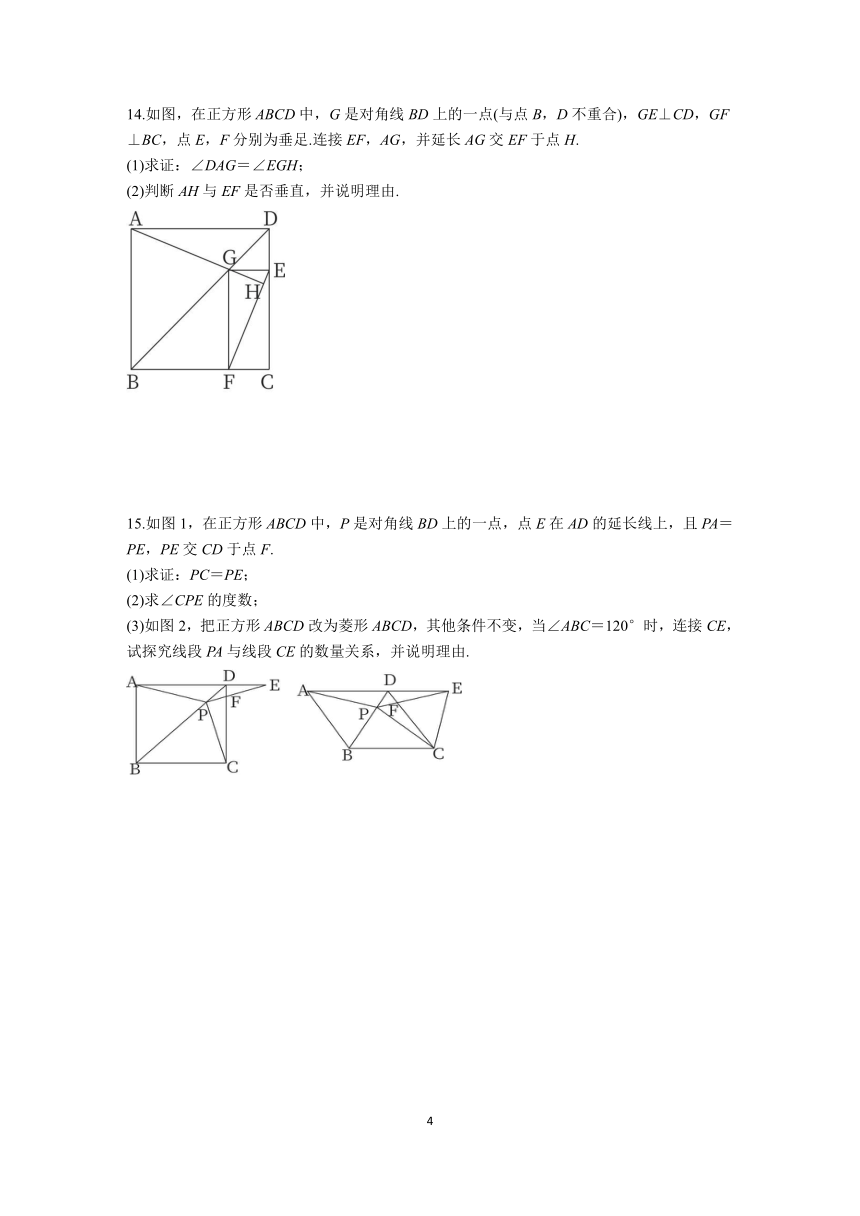
14.如图,在正方形ABCD中,G是对角线BD上的一点(与点B,D不重合),GE⊥CD,GF⊥BC,点E,F分别为垂足.连接EF,AG,并延长AG交EF于点H.
(1)求证:∠DAG=∠EGH;
(2)判断AH与EF是否垂直,并说明理由.
15.如图1,在正方形ABCD中,P是对角线BD上的一点,点E在AD的延长线上,且PA=PE,PE交CD于点F.
(1)求证:PC=PE;
(2)求∠CPE的度数;
(3)如图2,把正方形ABCD改为菱形ABCD,其他条件不变,当∠ABC=120°时,连接CE,试探究线段PA与线段CE的数量关系,并说明理由.
1
参考答案
一、选择题
1.正方形具有而菱形不一定有的性质是( B )
A.对角线互相垂直 B.对角线相等 C.对角相等 D.邻边相等
2.如图,P是正方形ABCD内位于对角线AC下方的一点,∠1=∠2,则∠BPC的度数为( A )
A.135° B.130° C.125° D.120°
3.如图,四边形ABCD为正方形,点A的坐标为(-1,0),点B,C,D分别在坐标轴上,则正方形的周长是( C )
A.4 B.3 C.4 D.2
4.如图,在正方形ABCD的外侧作等边△ABE,则∠BED的度数为( C )
A.15° B.35° C.45° D.55°
5.如图,正方形ABCD的边长为8,M在DC上,且DM=2,N是AC上一动点,则DN+MN的最小值为( B )
A.8 B.10 C.2 D.8
提示:连接BM交AC于点N(图略),此时DN+MN有最小值,且DN+MN=BM==10.
6.如图,将n个边长都为1 cm的正方形按如图所示摆放,点A1,A2,…,An分别是正方形对角线的交点,则n个这样的正方形重叠部分的面积和为( C )
…
A. cm2 B. cm2 C. cm2 D. cm2
7.如图,在正方形ABCD中,AB=3,E为对角线AC上的动点,以DE为边作正方形DEFG,H是CD上一点,且DH=,连接GH,则GH的最小值为( C )
A. B.2 C.1 D.2
提示:连接CG.证△ADE≌△CDG,得CG⊥AC,当GH⊥CG时,GH的值最小.
二、填空题
8.如图,以正方形ABCD的顶点A为圆心,以AD的长为半径画弧,交对角线AC于点E,再分别以点D,E为圆心,以大于的长为半径画弧,两弧交于点F,连接AF并延长,与BC的延长线交于点P,则∠P的度数为 .
【答案】 22.5°
9.如图,O为正方形ABCD对角线AC的中点,△ACE为等边三角形.若AB=2,则DE的长为 .
【答案】
10.如图,将边长为3的正方形ABCD沿其对角线AC平移,使A的对应点A'满足AA'=,则所得正方形与原正方形重叠部分的面积是 .
【答案】4
11.如图,正方形ABCD的边长为2,E为与点D不重合的动点,以DE为一边作正方形DEFG.设DE=d1,点F,G与点C的距离分别为d2,d3,则d1+d2+d3的最小值为 .
【答案】2
提示:连接AE,CG,CF,AC.易证△ADE≌△CDG(SAS),∴AE=CG,∴d1+d2+d3=AE+EF+CF,当点A,E,F,C在同一条直线上时,d1+d2+d3最小.
三、解答题
12.如图,在正方形ABCD中,点E,M,N分别在AB,BC,AD边上,CE=MN.求证:CE⊥MN.
证明:过点N作NF⊥BC于点F.
∵四边形ABCD是正方形,
∴NF=CD=BC.
易证Rt△BCE≌Rt△FNM(HL),
∴∠CON=∠NMF+∠BCE=∠NMF+∠FNM=90°,∴CE⊥MN.
13.如图,正方形ABCD,G是BC边上任意一点(不与B,C重合),DE⊥AG于点E,BF∥DE,且交AG于点F.求证:AF-BF=EF.
证明 ∵四边形ABCD是正方形,
∴AB=AD,∠BAF+∠DAE=90°.
∵DE⊥AG,∴∠DAE+∠ADE=90°,
∴∠ADE=∠BAF.
又BF∥DE,∴∠BFA=∠DEG=∠AED=90°,
∴△ABF≌△DAE(AAS),∴AE=BF,
∴AF-BF=AF-AE=EF.
14.如图,在正方形ABCD中,G是对角线BD上的一点(与点B,D不重合),GE⊥CD,GF⊥BC,点E,F分别为垂足.连接EF,AG,并延长AG交EF于点H.
(1)求证:∠DAG=∠EGH;
(2)判断AH与EF是否垂直,并说明理由.
解:(1)证明略.
(2)AH⊥EF.
理由:连接GC交EF于点O.
易得△ADG≌△CDG,四边形FCEG为矩形,
∴∠DAG=∠DCG,OE=OC,
∴∠OEC=∠DCG=∠DAG.
结合(1)得∠EGH=∠OEC,
∴∠EGH+∠GEH=∠OEC+∠GEH=∠GEC=90°,
∴∠GHE=90°,即AH⊥EF.
15.如图1,在正方形ABCD中,P是对角线BD上的一点,点E在AD的延长线上,且PA=PE,PE交CD于点F.
(1)求证:PC=PE;
(2)求∠CPE的度数;
(3)如图2,把正方形ABCD改为菱形ABCD,其他条件不变,当∠ABC=120°时,连接CE,试探究线段PA与线段CE的数量关系,并说明理由.
解:(1)易证△ABP≌△CBP,∴PA=PC.
∵PA=PE,∴PC=PE.
(2)∠CPE的度数为90°.
(3)PA=CE.
理由:易证△EPC是等边三角形,
∴PC=PE=CE.
∵PA=PE,∴PA=CE.
18.2.3 正方形
第1课时 正方形的性质
一、选择题
1.正方形具有而菱形不一定有的性质是( )
A.对角线互相垂直 B.对角线相等 C.对角相等 D.邻边相等
2.如图,P是正方形ABCD内位于对角线AC下方的一点,∠1=∠2,则∠BPC的度数为( )
A.135° B.130° C.125° D.120°
3.如图,四边形ABCD为正方形,点A的坐标为(-1,0),点B,C,D分别在坐标轴上,则正方形的周长是( )
A.4 B.3 C.4 D.2
4.如图,在正方形ABCD的外侧作等边△ABE,则∠BED的度数为( )
A.15° B.35° C.45° D.55°
5.如图,正方形ABCD的边长为8,M在DC上,且DM=2,N是AC上一动点,则DN+MN的最小值为( )
A.8 B.10 C.2 D.8
6.如图,将n个边长都为1 cm的正方形按如图所示摆放,点A1,A2,…,An分别是正方形对角线的交点,则n个这样的正方形重叠部分的面积和为( )
…
A. cm2 B. cm2 C. cm2 D. cm2
7.如图,在正方形ABCD中,AB=3,E为对角线AC上的动点,以DE为边作正方形DEFG,H是CD上一点,且DH=,连接GH,则GH的最小值为( )
A. B.2 C.1 D.2
二、填空题
8.如图,以正方形ABCD的顶点A为圆心,以AD的长为半径画弧,交对角线AC于点E,再分别以点D,E为圆心,以大于的长为半径画弧,两弧交于点F,连接AF并延长,与BC的延长线交于点P,则∠P的度数为 .
9.如图,O为正方形ABCD对角线AC的中点,△ACE为等边三角形.若AB=2,则DE的长为 .
10.如图,将边长为3的正方形ABCD沿其对角线AC平移,使A的对应点A'满足AA'=,则所得正方形与原正方形重叠部分的面积是 .
11.如图,正方形ABCD的边长为2,E为与点D不重合的动点,以DE为一边作正方形DEFG.设DE=d1,点F,G与点C的距离分别为d2,d3,则d1+d2+d3的最小值为 .
三、解答题
12.如图,在正方形ABCD中,点E,M,N分别在AB,BC,AD边上,CE=MN.求证:CE⊥MN.
13.如图,正方形ABCD,G是BC边上任意一点(不与B,C重合),DE⊥AG于点E,BF∥DE,且交AG于点F.求证:AF-BF=EF.
14.如图,在正方形ABCD中,G是对角线BD上的一点(与点B,D不重合),GE⊥CD,GF⊥BC,点E,F分别为垂足.连接EF,AG,并延长AG交EF于点H.
(1)求证:∠DAG=∠EGH;
(2)判断AH与EF是否垂直,并说明理由.
15.如图1,在正方形ABCD中,P是对角线BD上的一点,点E在AD的延长线上,且PA=PE,PE交CD于点F.
(1)求证:PC=PE;
(2)求∠CPE的度数;
(3)如图2,把正方形ABCD改为菱形ABCD,其他条件不变,当∠ABC=120°时,连接CE,试探究线段PA与线段CE的数量关系,并说明理由.
1
参考答案
一、选择题
1.正方形具有而菱形不一定有的性质是( B )
A.对角线互相垂直 B.对角线相等 C.对角相等 D.邻边相等
2.如图,P是正方形ABCD内位于对角线AC下方的一点,∠1=∠2,则∠BPC的度数为( A )
A.135° B.130° C.125° D.120°
3.如图,四边形ABCD为正方形,点A的坐标为(-1,0),点B,C,D分别在坐标轴上,则正方形的周长是( C )
A.4 B.3 C.4 D.2
4.如图,在正方形ABCD的外侧作等边△ABE,则∠BED的度数为( C )
A.15° B.35° C.45° D.55°
5.如图,正方形ABCD的边长为8,M在DC上,且DM=2,N是AC上一动点,则DN+MN的最小值为( B )
A.8 B.10 C.2 D.8
提示:连接BM交AC于点N(图略),此时DN+MN有最小值,且DN+MN=BM==10.
6.如图,将n个边长都为1 cm的正方形按如图所示摆放,点A1,A2,…,An分别是正方形对角线的交点,则n个这样的正方形重叠部分的面积和为( C )
…
A. cm2 B. cm2 C. cm2 D. cm2
7.如图,在正方形ABCD中,AB=3,E为对角线AC上的动点,以DE为边作正方形DEFG,H是CD上一点,且DH=,连接GH,则GH的最小值为( C )
A. B.2 C.1 D.2
提示:连接CG.证△ADE≌△CDG,得CG⊥AC,当GH⊥CG时,GH的值最小.
二、填空题
8.如图,以正方形ABCD的顶点A为圆心,以AD的长为半径画弧,交对角线AC于点E,再分别以点D,E为圆心,以大于的长为半径画弧,两弧交于点F,连接AF并延长,与BC的延长线交于点P,则∠P的度数为 .
【答案】 22.5°
9.如图,O为正方形ABCD对角线AC的中点,△ACE为等边三角形.若AB=2,则DE的长为 .
【答案】
10.如图,将边长为3的正方形ABCD沿其对角线AC平移,使A的对应点A'满足AA'=,则所得正方形与原正方形重叠部分的面积是 .
【答案】4
11.如图,正方形ABCD的边长为2,E为与点D不重合的动点,以DE为一边作正方形DEFG.设DE=d1,点F,G与点C的距离分别为d2,d3,则d1+d2+d3的最小值为 .
【答案】2
提示:连接AE,CG,CF,AC.易证△ADE≌△CDG(SAS),∴AE=CG,∴d1+d2+d3=AE+EF+CF,当点A,E,F,C在同一条直线上时,d1+d2+d3最小.
三、解答题
12.如图,在正方形ABCD中,点E,M,N分别在AB,BC,AD边上,CE=MN.求证:CE⊥MN.
证明:过点N作NF⊥BC于点F.
∵四边形ABCD是正方形,
∴NF=CD=BC.
易证Rt△BCE≌Rt△FNM(HL),
∴∠CON=∠NMF+∠BCE=∠NMF+∠FNM=90°,∴CE⊥MN.
13.如图,正方形ABCD,G是BC边上任意一点(不与B,C重合),DE⊥AG于点E,BF∥DE,且交AG于点F.求证:AF-BF=EF.
证明 ∵四边形ABCD是正方形,
∴AB=AD,∠BAF+∠DAE=90°.
∵DE⊥AG,∴∠DAE+∠ADE=90°,
∴∠ADE=∠BAF.
又BF∥DE,∴∠BFA=∠DEG=∠AED=90°,
∴△ABF≌△DAE(AAS),∴AE=BF,
∴AF-BF=AF-AE=EF.
14.如图,在正方形ABCD中,G是对角线BD上的一点(与点B,D不重合),GE⊥CD,GF⊥BC,点E,F分别为垂足.连接EF,AG,并延长AG交EF于点H.
(1)求证:∠DAG=∠EGH;
(2)判断AH与EF是否垂直,并说明理由.
解:(1)证明略.
(2)AH⊥EF.
理由:连接GC交EF于点O.
易得△ADG≌△CDG,四边形FCEG为矩形,
∴∠DAG=∠DCG,OE=OC,
∴∠OEC=∠DCG=∠DAG.
结合(1)得∠EGH=∠OEC,
∴∠EGH+∠GEH=∠OEC+∠GEH=∠GEC=90°,
∴∠GHE=90°,即AH⊥EF.
15.如图1,在正方形ABCD中,P是对角线BD上的一点,点E在AD的延长线上,且PA=PE,PE交CD于点F.
(1)求证:PC=PE;
(2)求∠CPE的度数;
(3)如图2,把正方形ABCD改为菱形ABCD,其他条件不变,当∠ABC=120°时,连接CE,试探究线段PA与线段CE的数量关系,并说明理由.
解:(1)易证△ABP≌△CBP,∴PA=PC.
∵PA=PE,∴PC=PE.
(2)∠CPE的度数为90°.
(3)PA=CE.
理由:易证△EPC是等边三角形,
∴PC=PE=CE.
∵PA=PE,∴PA=CE.
