人教版八年级下册18.2.3.2 正方形的判定 同步练习(含答案)
文档属性
| 名称 | 人教版八年级下册18.2.3.2 正方形的判定 同步练习(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 204.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-31 00:00:00 | ||
图片预览

文档简介
第十八章 平行四边形
18.2.3 正方形
第2课时 正方形的判定
一、选择题
1.四个角相等,四条边也相等的四边形一定是( ) A.正方形 B.菱形 C.矩形 D.平行四边形
2.下列命题正确的是( )
A.四边相等的四边形是正方形 B.四角相等的四边形是正方形
C.对角线相等的菱形是正方形 D.对角线垂直的平行四边形是正方形
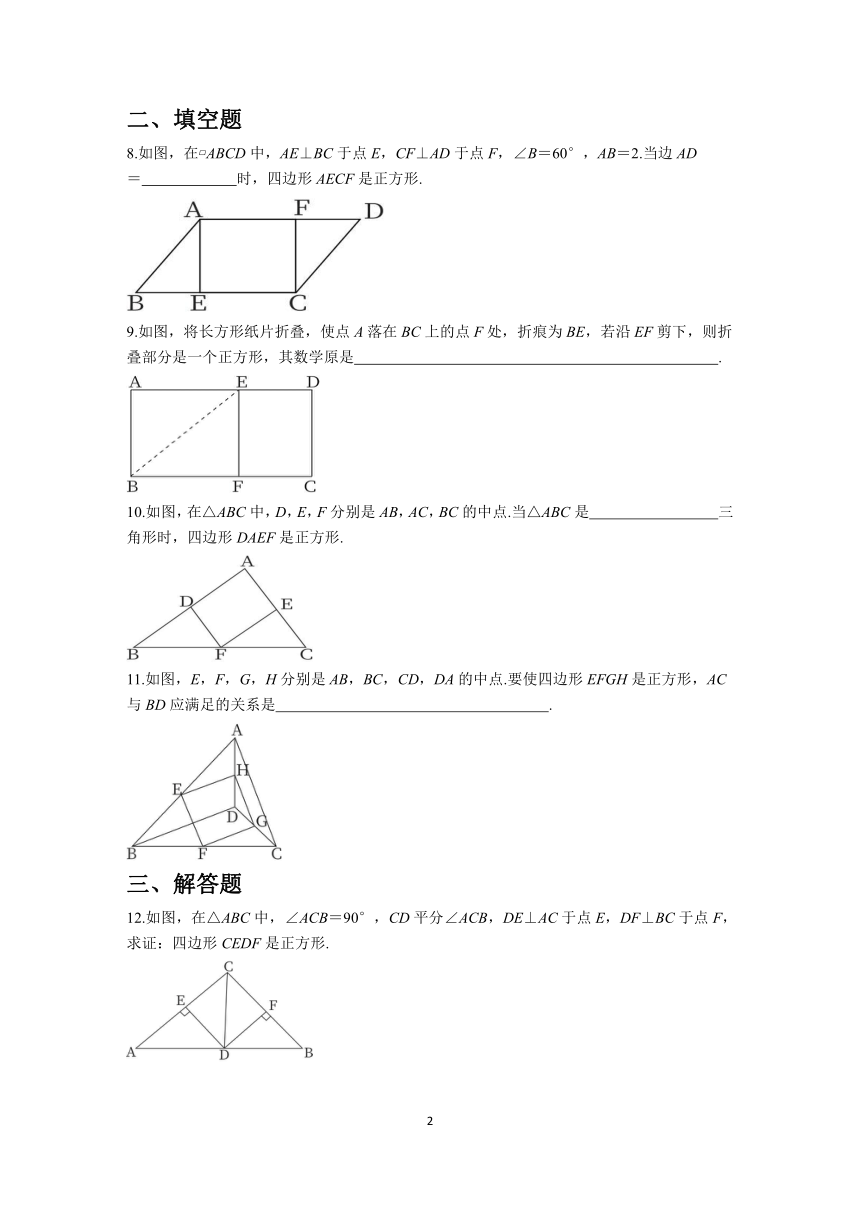
3.下列四个菱形中分别标注了部分数据,根据所标数据,可以判断菱形是正方形的是( )
4.添加下列一个条件,不能使矩形ABCD成为正方形的是( )
A.AB=AD B.AC⊥BD C.∠BAC=45° D.AC=2CD
5.小明在学习了正方形之后,给同桌小文出了道题.从下列四个条件①AB=BC;②∠ABC=90°;③AC=BD;④AC⊥BD中选两个作为补充条件,使 ABCD成为正方形,如图,现有下列四种选法,你认为其中错误的是( )
A.①② B.②③ C.①③ D.②④
6.用对折的方法证明一个四边形是正方形,则对折次数最少是( )
A.1次 B.2次 C.3次 D.4次
7.若四边形ABCD是平行四边形,则下列结论错误的是( )
A.当∠ABC=90°时,它是矩形 B.当AB=BC时,它是菱形
C.当AC⊥BD时,它是菱形 D.当AC=BD时,它是正方形
二、填空题
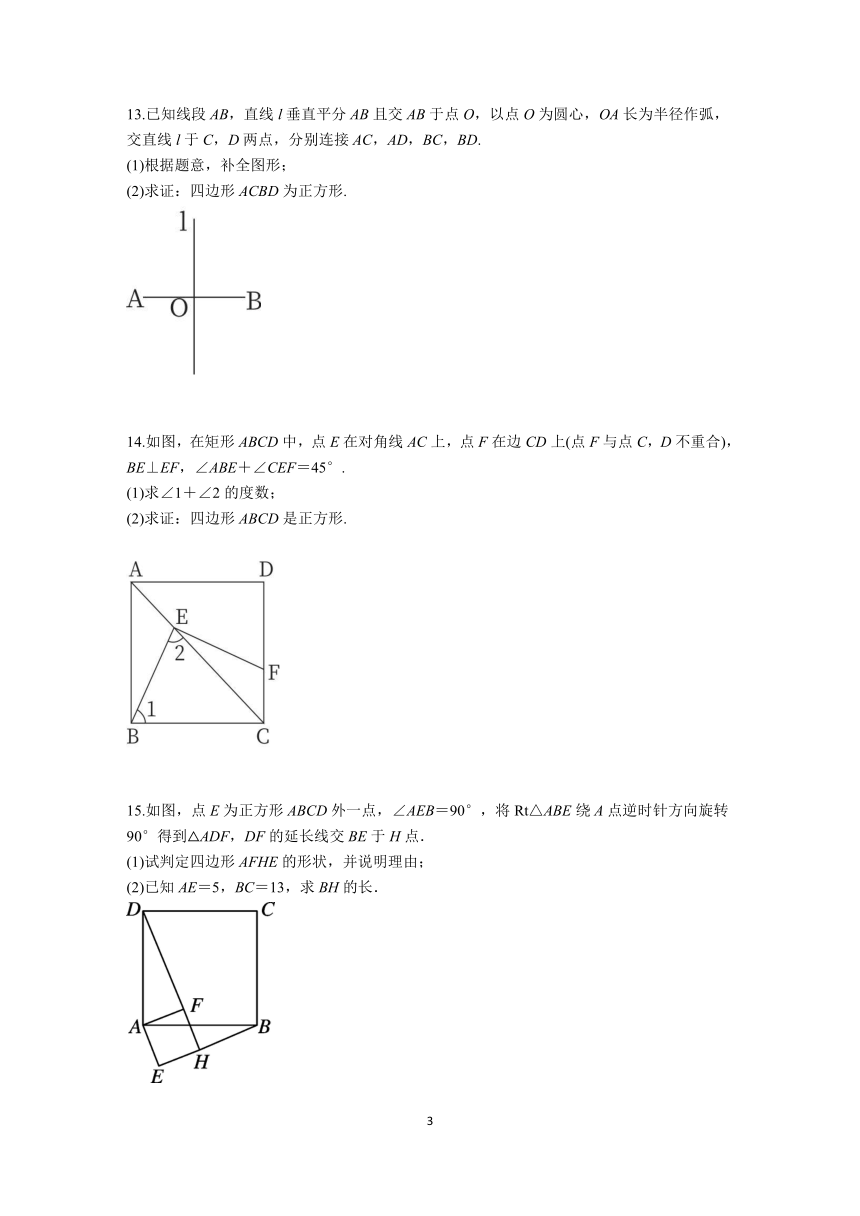
8.如图,在 ABCD中,AE⊥BC于点E,CF⊥AD于点F,∠B=60°,AB=2.当边AD= 时,四边形AECF是正方形.
9.如图,将长方形纸片折叠,使点A落在BC上的点F处,折痕为BE,若沿EF剪下,则折叠部分是一个正方形,其数学原是 .
10.如图,在△ABC中,D,E,F分别是AB,AC,BC的中点.当△ABC是 三角形时,四边形DAEF是正方形.
11.如图,E,F,G,H分别是AB,BC,CD,DA的中点.要使四边形EFGH是正方形,AC与BD应满足的关系是 .
三、解答题
12.如图,在△ABC中,∠ACB=90°,CD平分∠ACB,DE⊥AC于点E,DF⊥BC于点F,求证:四边形CEDF是正方形.
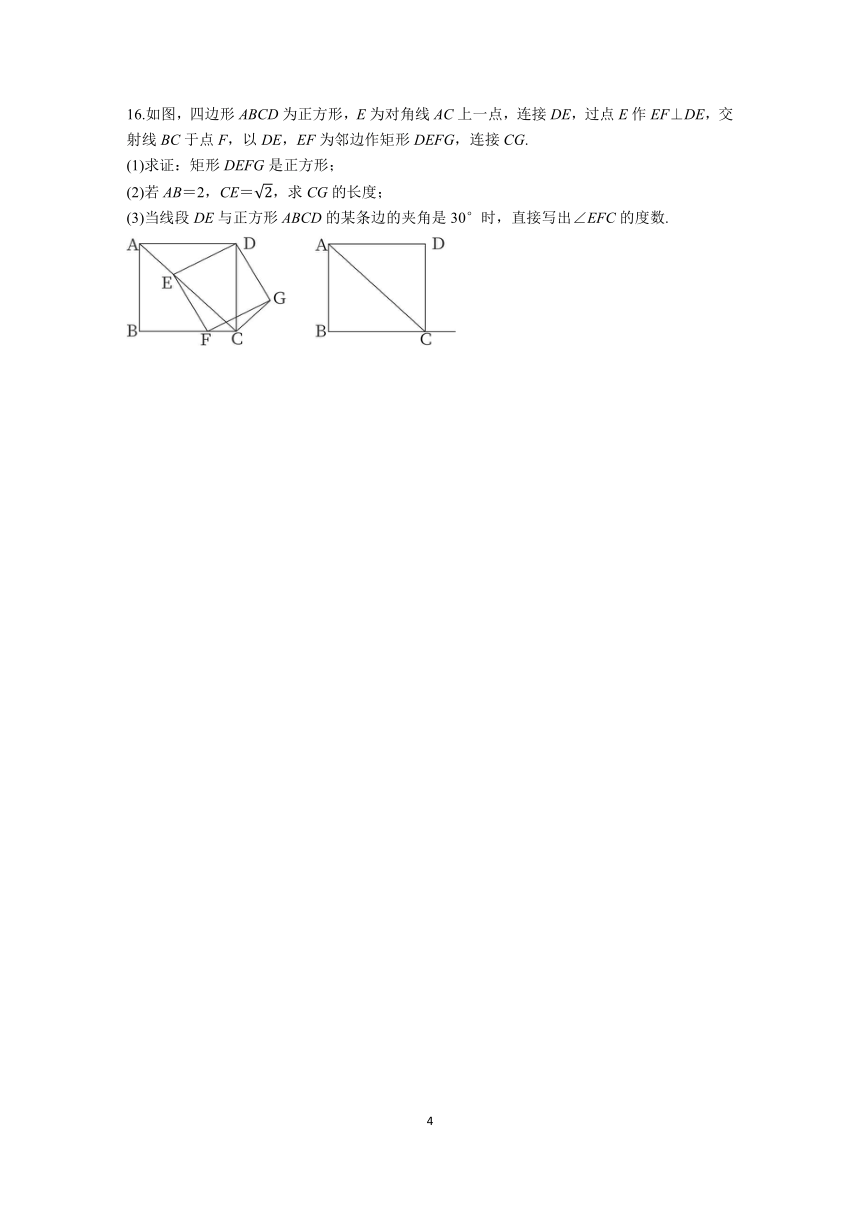
13.已知线段AB,直线l垂直平分AB且交AB于点O,以点O为圆心,OA长为半径作弧,交直线l于C,D两点,分别连接AC,AD,BC,BD.
(1)根据题意,补全图形;
(2)求证:四边形ACBD为正方形.
14.如图,在矩形ABCD中,点E在对角线AC上,点F在边CD上(点F与点C,D不重合),BE⊥EF,∠ABE+∠CEF=45°.
(1)求∠1+∠2的度数;
(2)求证:四边形ABCD是正方形.
15.如图,点E为正方形ABCD外一点,∠AEB=90°,将Rt△ABE绕A点逆时针方向旋转90°得到△ADF,DF的延长线交BE于H点.
(1)试判定四边形AFHE的形状,并说明理由;
(2)已知AE=5,BC=13,求BH的长.
16.如图,四边形ABCD为正方形,E为对角线AC上一点,连接DE,过点E作EF⊥DE,交射线BC于点F,以DE,EF为邻边作矩形DEFG,连接CG.
(1)求证:矩形DEFG是正方形;
(2)若AB=2,CE=,求CG的长度;
(3)当线段DE与正方形ABCD的某条边的夹角是30°时,直接写出∠EFC的度数.
1
参考答案
一、选择题
1.四个角相等,四条边也相等的四边形一定是( A ) A.正方形 B.菱形 C.矩形 D.平行四边形
2.下列命题正确的是( C )
A.四边相等的四边形是正方形 B.四角相等的四边形是正方形
C.对角线相等的菱形是正方形 D.对角线垂直的平行四边形是正方形
3.下列四个菱形中分别标注了部分数据,根据所标数据,可以判断菱形是正方形的是( B )
4.添加下列一个条件,不能使矩形ABCD成为正方形的是( D )
A.AB=AD B.AC⊥BD
C.∠BAC=45° D.AC=2CD
5.小明在学习了正方形之后,给同桌小文出了道题.从下列四个条件①AB=BC;②∠ABC=90°;③AC=BD;④AC⊥BD中选两个作为补充条件,使 ABCD成为正方形,如图,现有下列四种选法,你认为其中错误的是( B )
A.①② B.②③ C.①③ D.②④
6.用对折的方法证明一个四边形是正方形,则对折次数最少是( B )
A.1次 B.2次 C.3次 D.4次
7.若四边形ABCD是平行四边形,则下列结论错误的是( D )
A.当∠ABC=90°时,它是矩形 B.当AB=BC时,它是菱形
C.当AC⊥BD时,它是菱形 D.当AC=BD时,它是正方形
二、填空题
8.如图,在 ABCD中,AE⊥BC于点E,CF⊥AD于点F,∠B=60°,AB=2.当边AD= 时,四边形AECF是正方形.
【答案】+1
9.如图,将长方形纸片折叠,使点A落在BC上的点F处,折痕为BE,若沿EF剪下,则折叠部分是一个正方形,其数学原是 .
【答案】 邻边相等的矩形是正方形
10.如图,在△ABC中,D,E,F分别是AB,AC,BC的中点.当△ABC是 三角形时,四边形DAEF是正方形.
【答案】等腰直角
11.如图,E,F,G,H分别是AB,BC,CD,DA的中点.要使四边形EFGH是正方形,AC与BD应满足的关系是 .
【答案】 AC=BD且AC⊥BD
三、解答题
12.如图,在△ABC中,∠ACB=90°,CD平分∠ACB,DE⊥AC于点E,DF⊥BC于点F,求证:四边形CEDF是正方形.
证明:∵CD平分∠ACB,DE⊥AC,DF⊥BC,
∴DE=DF,∠DFC=∠DEC=90°.
又∵∠ACB=90°,∴四边形CEDF是矩形.
∵DE=DF,∴矩形CEDF是正方形.
13.已知线段AB,直线l垂直平分AB且交AB于点O,以点O为圆心,OA长为半径作弧,交直线l于C,D两点,分别连接AC,AD,BC,BD.
(1)根据题意,补全图形;
(2)求证:四边形ACBD为正方形.
解:(1)如图所示.
(2)∵直线l垂直平分AB,
∴OA=OB,CD⊥AB.
∵OA=OB=OC=OD,
∴AB=CD,∴四边形ACBD是矩形.
∵CD⊥AB,∴矩形ACBD为正方形.
14.如图,在矩形ABCD中,点E在对角线AC上,点F在边CD上(点F与点C,D不重合),BE⊥EF,∠ABE+∠CEF=45°.
(1)求∠1+∠2的度数;
(2)求证:四边形ABCD是正方形.
解:(1)∵四边形ABCD为矩形,
∴∠ABC=90°,∴∠ABE+∠1=90°.
∵BE⊥EF,∴∠CEF+∠2=90°.
∵∠ABE+∠CEF=45°,
∴∠1+∠2=90°+90°-45°=135°.
(2)易知∠ACB=180°-(∠1+∠2)=45°.
∵∠ABC=90°,∴∠BAC=45°,
∴∠ACB=∠BAC,∴AB=BC,
∴矩形ABCD是正方形.
15.如图,点E为正方形ABCD外一点,∠AEB=90°,将Rt△ABE绕A点逆时针方向旋转90°得到△ADF,DF的延长线交BE于H点.
(1)试判定四边形AFHE的形状,并说明理由;
(2)已知AE=5,BC=13,求BH的长.
解:(1)四边形AFHE是正方形.理由如下:
∵Rt△ABE绕A点逆时针方向旋转90°得到△ADF,
∴Rt△ABE≌Rt△ADF,
∴∠AEB=∠AFD=90°=∠AFH,
∠DAF=∠BAE,
又∵∠DAF+∠FAB=90°,
∴∠BAE+∠FAB=90°,∴∠FAE=90°,
∴四边形AFHE是矩形,
又∵AE=AF,∴矩形AFHE是正方形.
(2)在Rt△ABE中,
BE===12,
由(1)知EH=AE,
∴BH=BE-EH=12-5=7.
16.如图,四边形ABCD为正方形,E为对角线AC上一点,连接DE,过点E作EF⊥DE,交射线BC于点F,以DE,EF为邻边作矩形DEFG,连接CG.
(1)求证:矩形DEFG是正方形;
(2)若AB=2,CE=,求CG的长度;
(3)当线段DE与正方形ABCD的某条边的夹角是30°时,直接写出∠EFC的度数.
解:(1)过点E作EP⊥CD于点P,EQ⊥BC于点Q,则四边形PEQC为矩形,∴∠QEP=90°.
∵∠DCA=∠BCA,∴EQ=EP.
∵∠QEF+∠FEP=∠PED+∠FEP=90°,
∴∠QEF=∠PED,
∴△EQF≌△EPD(ASA),
∴EF=ED,∴矩形DEFG是正方形.
(2)在Rt△ABC中,AC==2.
∵CE=,∴AE=CE,∴DE⊥AC,
∴点F与点C重合,∴CG=CE=.
(3)∠EFC的度数为120°或30°.
18.2.3 正方形
第2课时 正方形的判定
一、选择题
1.四个角相等,四条边也相等的四边形一定是( ) A.正方形 B.菱形 C.矩形 D.平行四边形
2.下列命题正确的是( )
A.四边相等的四边形是正方形 B.四角相等的四边形是正方形
C.对角线相等的菱形是正方形 D.对角线垂直的平行四边形是正方形
3.下列四个菱形中分别标注了部分数据,根据所标数据,可以判断菱形是正方形的是( )
4.添加下列一个条件,不能使矩形ABCD成为正方形的是( )
A.AB=AD B.AC⊥BD C.∠BAC=45° D.AC=2CD
5.小明在学习了正方形之后,给同桌小文出了道题.从下列四个条件①AB=BC;②∠ABC=90°;③AC=BD;④AC⊥BD中选两个作为补充条件,使 ABCD成为正方形,如图,现有下列四种选法,你认为其中错误的是( )
A.①② B.②③ C.①③ D.②④
6.用对折的方法证明一个四边形是正方形,则对折次数最少是( )
A.1次 B.2次 C.3次 D.4次
7.若四边形ABCD是平行四边形,则下列结论错误的是( )
A.当∠ABC=90°时,它是矩形 B.当AB=BC时,它是菱形
C.当AC⊥BD时,它是菱形 D.当AC=BD时,它是正方形
二、填空题
8.如图,在 ABCD中,AE⊥BC于点E,CF⊥AD于点F,∠B=60°,AB=2.当边AD= 时,四边形AECF是正方形.
9.如图,将长方形纸片折叠,使点A落在BC上的点F处,折痕为BE,若沿EF剪下,则折叠部分是一个正方形,其数学原是 .
10.如图,在△ABC中,D,E,F分别是AB,AC,BC的中点.当△ABC是 三角形时,四边形DAEF是正方形.
11.如图,E,F,G,H分别是AB,BC,CD,DA的中点.要使四边形EFGH是正方形,AC与BD应满足的关系是 .
三、解答题
12.如图,在△ABC中,∠ACB=90°,CD平分∠ACB,DE⊥AC于点E,DF⊥BC于点F,求证:四边形CEDF是正方形.
13.已知线段AB,直线l垂直平分AB且交AB于点O,以点O为圆心,OA长为半径作弧,交直线l于C,D两点,分别连接AC,AD,BC,BD.
(1)根据题意,补全图形;
(2)求证:四边形ACBD为正方形.
14.如图,在矩形ABCD中,点E在对角线AC上,点F在边CD上(点F与点C,D不重合),BE⊥EF,∠ABE+∠CEF=45°.
(1)求∠1+∠2的度数;
(2)求证:四边形ABCD是正方形.
15.如图,点E为正方形ABCD外一点,∠AEB=90°,将Rt△ABE绕A点逆时针方向旋转90°得到△ADF,DF的延长线交BE于H点.
(1)试判定四边形AFHE的形状,并说明理由;
(2)已知AE=5,BC=13,求BH的长.
16.如图,四边形ABCD为正方形,E为对角线AC上一点,连接DE,过点E作EF⊥DE,交射线BC于点F,以DE,EF为邻边作矩形DEFG,连接CG.
(1)求证:矩形DEFG是正方形;
(2)若AB=2,CE=,求CG的长度;
(3)当线段DE与正方形ABCD的某条边的夹角是30°时,直接写出∠EFC的度数.
1
参考答案
一、选择题
1.四个角相等,四条边也相等的四边形一定是( A ) A.正方形 B.菱形 C.矩形 D.平行四边形
2.下列命题正确的是( C )
A.四边相等的四边形是正方形 B.四角相等的四边形是正方形
C.对角线相等的菱形是正方形 D.对角线垂直的平行四边形是正方形
3.下列四个菱形中分别标注了部分数据,根据所标数据,可以判断菱形是正方形的是( B )
4.添加下列一个条件,不能使矩形ABCD成为正方形的是( D )
A.AB=AD B.AC⊥BD
C.∠BAC=45° D.AC=2CD
5.小明在学习了正方形之后,给同桌小文出了道题.从下列四个条件①AB=BC;②∠ABC=90°;③AC=BD;④AC⊥BD中选两个作为补充条件,使 ABCD成为正方形,如图,现有下列四种选法,你认为其中错误的是( B )
A.①② B.②③ C.①③ D.②④
6.用对折的方法证明一个四边形是正方形,则对折次数最少是( B )
A.1次 B.2次 C.3次 D.4次
7.若四边形ABCD是平行四边形,则下列结论错误的是( D )
A.当∠ABC=90°时,它是矩形 B.当AB=BC时,它是菱形
C.当AC⊥BD时,它是菱形 D.当AC=BD时,它是正方形
二、填空题
8.如图,在 ABCD中,AE⊥BC于点E,CF⊥AD于点F,∠B=60°,AB=2.当边AD= 时,四边形AECF是正方形.
【答案】+1
9.如图,将长方形纸片折叠,使点A落在BC上的点F处,折痕为BE,若沿EF剪下,则折叠部分是一个正方形,其数学原是 .
【答案】 邻边相等的矩形是正方形
10.如图,在△ABC中,D,E,F分别是AB,AC,BC的中点.当△ABC是 三角形时,四边形DAEF是正方形.
【答案】等腰直角
11.如图,E,F,G,H分别是AB,BC,CD,DA的中点.要使四边形EFGH是正方形,AC与BD应满足的关系是 .
【答案】 AC=BD且AC⊥BD
三、解答题
12.如图,在△ABC中,∠ACB=90°,CD平分∠ACB,DE⊥AC于点E,DF⊥BC于点F,求证:四边形CEDF是正方形.
证明:∵CD平分∠ACB,DE⊥AC,DF⊥BC,
∴DE=DF,∠DFC=∠DEC=90°.
又∵∠ACB=90°,∴四边形CEDF是矩形.
∵DE=DF,∴矩形CEDF是正方形.
13.已知线段AB,直线l垂直平分AB且交AB于点O,以点O为圆心,OA长为半径作弧,交直线l于C,D两点,分别连接AC,AD,BC,BD.
(1)根据题意,补全图形;
(2)求证:四边形ACBD为正方形.
解:(1)如图所示.
(2)∵直线l垂直平分AB,
∴OA=OB,CD⊥AB.
∵OA=OB=OC=OD,
∴AB=CD,∴四边形ACBD是矩形.
∵CD⊥AB,∴矩形ACBD为正方形.
14.如图,在矩形ABCD中,点E在对角线AC上,点F在边CD上(点F与点C,D不重合),BE⊥EF,∠ABE+∠CEF=45°.
(1)求∠1+∠2的度数;
(2)求证:四边形ABCD是正方形.
解:(1)∵四边形ABCD为矩形,
∴∠ABC=90°,∴∠ABE+∠1=90°.
∵BE⊥EF,∴∠CEF+∠2=90°.
∵∠ABE+∠CEF=45°,
∴∠1+∠2=90°+90°-45°=135°.
(2)易知∠ACB=180°-(∠1+∠2)=45°.
∵∠ABC=90°,∴∠BAC=45°,
∴∠ACB=∠BAC,∴AB=BC,
∴矩形ABCD是正方形.
15.如图,点E为正方形ABCD外一点,∠AEB=90°,将Rt△ABE绕A点逆时针方向旋转90°得到△ADF,DF的延长线交BE于H点.
(1)试判定四边形AFHE的形状,并说明理由;
(2)已知AE=5,BC=13,求BH的长.
解:(1)四边形AFHE是正方形.理由如下:
∵Rt△ABE绕A点逆时针方向旋转90°得到△ADF,
∴Rt△ABE≌Rt△ADF,
∴∠AEB=∠AFD=90°=∠AFH,
∠DAF=∠BAE,
又∵∠DAF+∠FAB=90°,
∴∠BAE+∠FAB=90°,∴∠FAE=90°,
∴四边形AFHE是矩形,
又∵AE=AF,∴矩形AFHE是正方形.
(2)在Rt△ABE中,
BE===12,
由(1)知EH=AE,
∴BH=BE-EH=12-5=7.
16.如图,四边形ABCD为正方形,E为对角线AC上一点,连接DE,过点E作EF⊥DE,交射线BC于点F,以DE,EF为邻边作矩形DEFG,连接CG.
(1)求证:矩形DEFG是正方形;
(2)若AB=2,CE=,求CG的长度;
(3)当线段DE与正方形ABCD的某条边的夹角是30°时,直接写出∠EFC的度数.
解:(1)过点E作EP⊥CD于点P,EQ⊥BC于点Q,则四边形PEQC为矩形,∴∠QEP=90°.
∵∠DCA=∠BCA,∴EQ=EP.
∵∠QEF+∠FEP=∠PED+∠FEP=90°,
∴∠QEF=∠PED,
∴△EQF≌△EPD(ASA),
∴EF=ED,∴矩形DEFG是正方形.
(2)在Rt△ABC中,AC==2.
∵CE=,∴AE=CE,∴DE⊥AC,
∴点F与点C重合,∴CG=CE=.
(3)∠EFC的度数为120°或30°.
