山东省临沂市费县2023-2024学年高二下学期3月质量检测数学试题(含答案)
文档属性
| 名称 | 山东省临沂市费县2023-2024学年高二下学期3月质量检测数学试题(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 199.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-31 15:16:13 | ||
图片预览




文档简介
费县2023-2024学年高二下学期3月质量检测
数 学(B) 2024.3.28
一、选择题:本题共 8 小题,每小题 5 分,共 40 分。在每小题给出的四个选项中,只有一项是符合题目要 求的。
1 、若 C8 =C-8 ,则 x 的值为( )
A .3 或 5 B .6 C .4 或 9 D .18
2. 若f (x) = ln (一x) ,则f, (一2024) = ( )
A . 一 1 B .-2024 C . 1 D .2024
2024 2024
3.京剧,又称平剧、京戏等,中国国粹之一,是中国影响最大的戏曲剧种,分布地以北京为中心,遍及全国 各地.京剧班社有“七行七科”之说:七行即生行、旦行(亦称占行) 、净行、丑行、杂行、武行、流行.某次京 剧表演结束后 7 个表演者(七行中每行 1 人)排成一排合影留念,其中净行、丑行、杂行互不相邻,则不同的
排法总数是( )
A .144 B .240 C .576 D .1440
4. 中国灯笼又统称为灯彩,主要有宫灯、纱灯、 吊灯等种类.现有 4 名学生,每人从宫灯、纱灯、吊灯中
选购 1 种,则不同的选购方式有( )
A . 34 种 B . 43 种 C .3 x 2 x 1种 D . 4 x 3 x 2 种
的图象画在同一直角坐标系中,得到 2
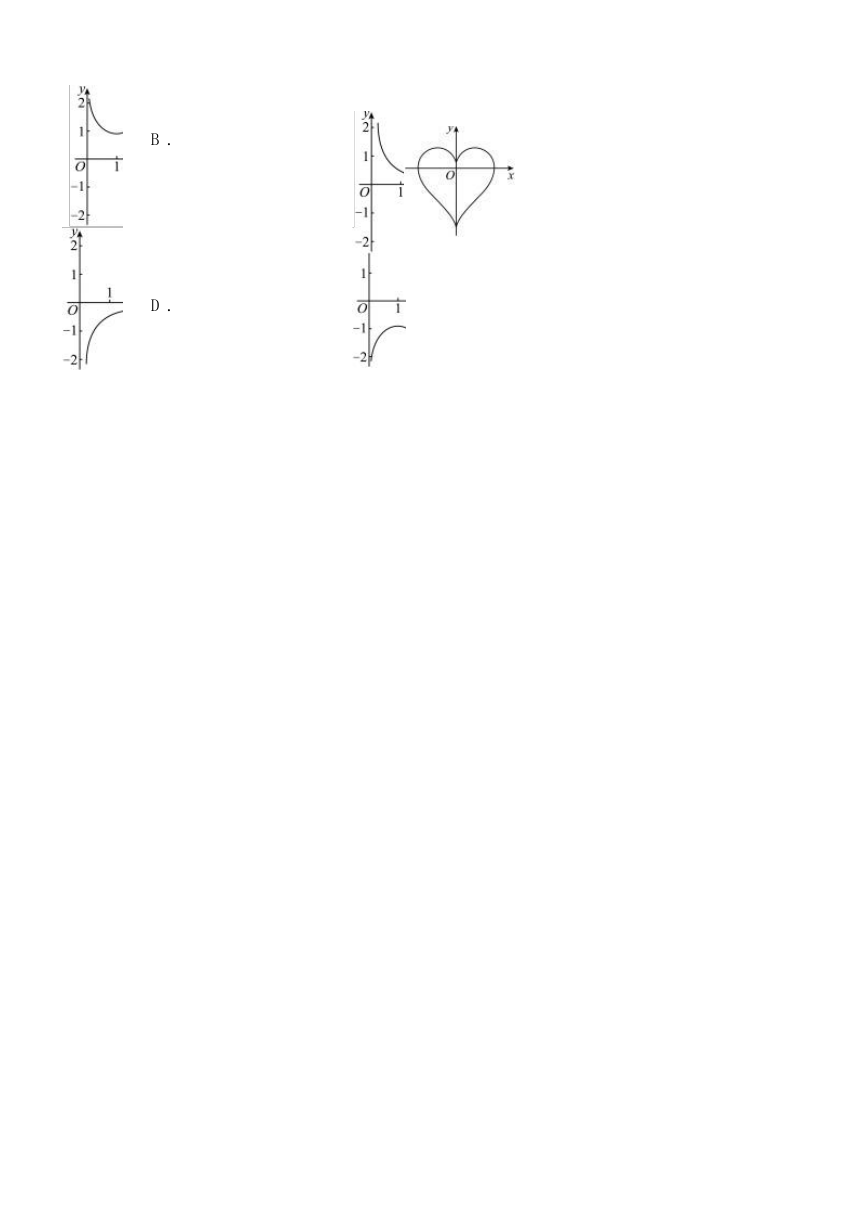
如图的“心形线” .观察图形,当x > 0 时, g (x) 的导函数g,(x) 的图象大致为( )
A .
C .
B .
D .
6.从 10 名大学毕业生中选 3 人担任村主任助理,则甲、乙至少有 1 人入选,而丙没有入选的选法种数为 ( )
A .28 B .49 C .56 D .85
7. (x +1)2 (|(x - 6 的展开式中含 x3 项的系数为( )
A. 20 B. -20 C. 30 D. -30
8. 若对任意的x1 , x2 e (m, +伪) ,且x1 < x2 , < 2 ,则实数m 的取值范围是( )
A . |(e , e)| B . |Le , e」| C . |Le , +伪)| D . |(e , +伪)|
二、选择题:本题共 3 小题,每小题 6 分,共 18 分。在每小题给出的选项中,有多项符合题目要求。全部
选对的得 6 分,部分选对的得部分分,有选错的得 0 分。
9 .下列函数中,既是偶函数,又在区间(0, +伪) 上单调递增的是( )
A . y = ln x B . y = lnx C . y = x-2 D . y = ex + e-x
10.下列结论中正确的是( )
A .若y = cos ,则y, = sin B .若y = ,则y, =
C .若y = ,则y, = D .若y = ln (2x +1) ,则y , =
11. 现有带有编号1、2、3、4、5 的五个球及四个不同的盒子,则下列表述正确的有( )
A .全部投入 4 个不同的盒子里,允许有空盒,共有45 种放法
B .全部投入 4 个不同的盒子里,没有空盒,共有C . A 种不同的放法
C .将其中的 4 个球投入 4 个盒子里的一个(另一个球不投入),共有C . C种放法
D .全部投入 2 个不同的盒子里,每盒至少一个,共有C . A 种放法
三、填空题:本题共 3 小题,每小题 5 分,共 15 分。
12.在二项式 ( - )10 的展开式中,第 4 项的系数为 .
13. 函数f(x) = sin 2x + 2 cos x 在(0, π) 上的单调递增区间为 .
1 4 .已 知 f ( x ) = x ( x - c ) 在 x = 2 处 有 极 小 值 , 则 c = .
四、解答题:本题共 5 小题,共 77 分。解答应写出文字说明、证明过程或演算步骤。
15.(13 分).在 ( - )8 的展开式中,
( 1)求二项式系数最大的项.
(2)求系数最大的项.
16.(15 分)设 f(x)=a(x-5)2+6ln x,其中 a∈R,曲线 y=f(x)在点(1,f(1))处的切线与 y轴相交于点
(0,6).
(1)确定 a的值;
(2)求函数 f(x)的单调区间与极值.
( 15 分) 函数f(x) = (x +1)ex .
(1)判断函数 f (x) 的单调性,并求出 f (x) 的极值;
(2)画出函数 f (x) 的大致图象;
(3)求出方程 f(x) = a(a e R) 解的个数
18.(17分)设函数f (x) = 2x 一 一 a lnx(ae R).
(1)讨论f (x)的单调性.
(2)若f (x)有两个极值点x1,x2,记过A(x1,f( x1) ,) B (x2, f( x2) 两)点的直线的斜率为 k 若x2 e (1, ),证明: k < 0.
19.(17 分)已知函数f (x ) = x2 + ax 一 xlnx 的导函数为f , (x ) .
( 1)若a = 一1 ,求曲线y = f (x) 在点(1, f (1)) 处的切线方程.
(2)若f , (x ) 存在两个不同的零点x1 , x2 ,
(ⅰ) 求实数a 的取值范围;
(ⅱ) 证明:x1 + x2 >1 .
高二年级三月份质量检测试题 数学答案(B)
一、选择题:本题共 8 小题,每小题 5 分,共 40 分.
题目 1 2 3 4 5 6 7 8
答案 C A D A A B C C
二、多选题:本题共 3 小题,每小题 6 分,共 18 分.
9 AD 10.ACD 11. ABD
三、填空题:本题共 3 小题,每小题 5 分,共 15 分.
12. -405 13.-4 14. 2
四、解答题:本题共 5 小题,共 77 分.
15. (1)二项式系数最大的项为中间项,即第 5 项, T5 = (-2)4 Cx-6 = 1120x-6 .
(2)展开式中的第 6 项和第 7 项系数的绝对值最大,而第 6 项的系数为负,第 7 项的系数
为正,所以系数最大的项为第 7 项T7 = (-2)6 Cx- 11 = 1792x- 11
16. (1)因为 f(x)=a(x-5)2+6ln x,所以 f′ (x)=2a(x-5)+
令 x=1,得 f(1)=16a,f′ (1)=6-8a,
所以曲线 y=f(x)在点(1,f(1))处的切线方程为:y-16a= (6-8a)(x-1),
由点(0,6)在切线上,可得 6-16a=8a-6,故 a= .
(2)由(1)知,f(x)= (x-5)2+6ln x(x>0),
f′ (x)=x-5+= ,令 f′ (x)=0,解得 x1 =2,x2 =3.
当 03 时,f′ (x)>0,故 f(x)的单调递增区间为(0,2), (3,+ ∞);
当 2=2 处取得极大值 f(2)=9+6ln 2,在 x=3 处取得极小值 f(3)=2+6ln 3.
17.见课本 95 页
18、
19.解:(1)若a = -1 ,则f (x) = x2 - x - xlnx ,f, (x ) = 2x -lnx - 2 ,
可得f, (1) = 0 ,且f (1) = 0 ,
所以曲线y = f (x) 在点(1, f (1)) 处的切线方程为y = 0 . 3 分
(2)(ⅰ) 由题意可知:f, (x ) = 2x -lnx + a - 1,
设g (x ) = 2x -lnx + a - 1 ,则g , (x ) = 2 - , x > 0
令g,(x) = 0 ,得x = ,
当x e(|(0, 时,g,(x) < 0 ,当x e , +伪 上,g,(x) > 0,
则g (x) 在(|(0, 上单调递减,在 , +伪上单调递增,
可得g(x) > g = 2 x -ln + a - 1 = a + ln2.
且当x 喻 0 或x 喻 +伪 时,g (x) 喻 +伪,
若g (x) 有两个零点,则a + ln2 < 0 ,解得a < -ln2 ,
所以a 的取值范围为(-伪, -ln2) . ..........9 分
(ⅱ) 由题意及(ⅰ) 知,存在不同的x1 , x2 e (0, +伪) ,使得g (x1 ) = g (x2 ) ,
不妨设x1 < x2 ,即x1 e (|(0, , x2 e , +伪 ,则
1- x1 e , 1 , .................... 11 分
设G(x) = g (x) - g (1 - x) , x e(|(0, ,
则G,(x ) = g,(x ) + g,(1 - x ) = 4
1 1
x 1 - x
1
x (1 - x ) ,
................. 13 分
当x e(|(0, 时, e (4, +伪) ,可知G, (x) < 0在(|(0, 上恒成立,
则G(x)在(|(0, 内单调递减,
可得G(x) > G = 0 ,
即g (x) > g (1- x), x = (|(0, , ................... 15 分
又因为x1 = (|(0, , x2 = , +伪 ,1- x1 = , 1 ,则g (x1 ) = g (x2 ) > g (1 - x1 ) ,
且g (x) 在 , +伪上单调递增,可得x2 > 1- x1 ,
即x1 + x2 >1 . ...17 分
数 学(B) 2024.3.28
一、选择题:本题共 8 小题,每小题 5 分,共 40 分。在每小题给出的四个选项中,只有一项是符合题目要 求的。
1 、若 C8 =C-8 ,则 x 的值为( )
A .3 或 5 B .6 C .4 或 9 D .18
2. 若f (x) = ln (一x) ,则f, (一2024) = ( )
A . 一 1 B .-2024 C . 1 D .2024
2024 2024
3.京剧,又称平剧、京戏等,中国国粹之一,是中国影响最大的戏曲剧种,分布地以北京为中心,遍及全国 各地.京剧班社有“七行七科”之说:七行即生行、旦行(亦称占行) 、净行、丑行、杂行、武行、流行.某次京 剧表演结束后 7 个表演者(七行中每行 1 人)排成一排合影留念,其中净行、丑行、杂行互不相邻,则不同的
排法总数是( )
A .144 B .240 C .576 D .1440
4. 中国灯笼又统称为灯彩,主要有宫灯、纱灯、 吊灯等种类.现有 4 名学生,每人从宫灯、纱灯、吊灯中
选购 1 种,则不同的选购方式有( )
A . 34 种 B . 43 种 C .3 x 2 x 1种 D . 4 x 3 x 2 种
的图象画在同一直角坐标系中,得到 2
如图的“心形线” .观察图形,当x > 0 时, g (x) 的导函数g,(x) 的图象大致为( )
A .
C .
B .
D .
6.从 10 名大学毕业生中选 3 人担任村主任助理,则甲、乙至少有 1 人入选,而丙没有入选的选法种数为 ( )
A .28 B .49 C .56 D .85
7. (x +1)2 (|(x - 6 的展开式中含 x3 项的系数为( )
A. 20 B. -20 C. 30 D. -30
8. 若对任意的x1 , x2 e (m, +伪) ,且x1 < x2 , < 2 ,则实数m 的取值范围是( )
A . |(e , e)| B . |Le , e」| C . |Le , +伪)| D . |(e , +伪)|
二、选择题:本题共 3 小题,每小题 6 分,共 18 分。在每小题给出的选项中,有多项符合题目要求。全部
选对的得 6 分,部分选对的得部分分,有选错的得 0 分。
9 .下列函数中,既是偶函数,又在区间(0, +伪) 上单调递增的是( )
A . y = ln x B . y = lnx C . y = x-2 D . y = ex + e-x
10.下列结论中正确的是( )
A .若y = cos ,则y, = sin B .若y = ,则y, =
C .若y = ,则y, = D .若y = ln (2x +1) ,则y , =
11. 现有带有编号1、2、3、4、5 的五个球及四个不同的盒子,则下列表述正确的有( )
A .全部投入 4 个不同的盒子里,允许有空盒,共有45 种放法
B .全部投入 4 个不同的盒子里,没有空盒,共有C . A 种不同的放法
C .将其中的 4 个球投入 4 个盒子里的一个(另一个球不投入),共有C . C种放法
D .全部投入 2 个不同的盒子里,每盒至少一个,共有C . A 种放法
三、填空题:本题共 3 小题,每小题 5 分,共 15 分。
12.在二项式 ( - )10 的展开式中,第 4 项的系数为 .
13. 函数f(x) = sin 2x + 2 cos x 在(0, π) 上的单调递增区间为 .
1 4 .已 知 f ( x ) = x ( x - c ) 在 x = 2 处 有 极 小 值 , 则 c = .
四、解答题:本题共 5 小题,共 77 分。解答应写出文字说明、证明过程或演算步骤。
15.(13 分).在 ( - )8 的展开式中,
( 1)求二项式系数最大的项.
(2)求系数最大的项.
16.(15 分)设 f(x)=a(x-5)2+6ln x,其中 a∈R,曲线 y=f(x)在点(1,f(1))处的切线与 y轴相交于点
(0,6).
(1)确定 a的值;
(2)求函数 f(x)的单调区间与极值.
( 15 分) 函数f(x) = (x +1)ex .
(1)判断函数 f (x) 的单调性,并求出 f (x) 的极值;
(2)画出函数 f (x) 的大致图象;
(3)求出方程 f(x) = a(a e R) 解的个数
18.(17分)设函数f (x) = 2x 一 一 a lnx(ae R).
(1)讨论f (x)的单调性.
(2)若f (x)有两个极值点x1,x2,记过A(x1,f( x1) ,) B (x2, f( x2) 两)点的直线的斜率为 k 若x2 e (1, ),证明: k < 0.
19.(17 分)已知函数f (x ) = x2 + ax 一 xlnx 的导函数为f , (x ) .
( 1)若a = 一1 ,求曲线y = f (x) 在点(1, f (1)) 处的切线方程.
(2)若f , (x ) 存在两个不同的零点x1 , x2 ,
(ⅰ) 求实数a 的取值范围;
(ⅱ) 证明:x1 + x2 >1 .
高二年级三月份质量检测试题 数学答案(B)
一、选择题:本题共 8 小题,每小题 5 分,共 40 分.
题目 1 2 3 4 5 6 7 8
答案 C A D A A B C C
二、多选题:本题共 3 小题,每小题 6 分,共 18 分.
9 AD 10.ACD 11. ABD
三、填空题:本题共 3 小题,每小题 5 分,共 15 分.
12. -405 13.-4 14. 2
四、解答题:本题共 5 小题,共 77 分.
15. (1)二项式系数最大的项为中间项,即第 5 项, T5 = (-2)4 Cx-6 = 1120x-6 .
(2)展开式中的第 6 项和第 7 项系数的绝对值最大,而第 6 项的系数为负,第 7 项的系数
为正,所以系数最大的项为第 7 项T7 = (-2)6 Cx- 11 = 1792x- 11
16. (1)因为 f(x)=a(x-5)2+6ln x,所以 f′ (x)=2a(x-5)+
令 x=1,得 f(1)=16a,f′ (1)=6-8a,
所以曲线 y=f(x)在点(1,f(1))处的切线方程为:y-16a= (6-8a)(x-1),
由点(0,6)在切线上,可得 6-16a=8a-6,故 a= .
(2)由(1)知,f(x)= (x-5)2+6ln x(x>0),
f′ (x)=x-5+= ,令 f′ (x)=0,解得 x1 =2,x2 =3.
当 0
当 2
17.见课本 95 页
18、
19.解:(1)若a = -1 ,则f (x) = x2 - x - xlnx ,f, (x ) = 2x -lnx - 2 ,
可得f, (1) = 0 ,且f (1) = 0 ,
所以曲线y = f (x) 在点(1, f (1)) 处的切线方程为y = 0 . 3 分
(2)(ⅰ) 由题意可知:f, (x ) = 2x -lnx + a - 1,
设g (x ) = 2x -lnx + a - 1 ,则g , (x ) = 2 - , x > 0
令g,(x) = 0 ,得x = ,
当x e(|(0, 时,g,(x) < 0 ,当x e , +伪 上,g,(x) > 0,
则g (x) 在(|(0, 上单调递减,在 , +伪上单调递增,
可得g(x) > g = 2 x -ln + a - 1 = a + ln2.
且当x 喻 0 或x 喻 +伪 时,g (x) 喻 +伪,
若g (x) 有两个零点,则a + ln2 < 0 ,解得a < -ln2 ,
所以a 的取值范围为(-伪, -ln2) . ..........9 分
(ⅱ) 由题意及(ⅰ) 知,存在不同的x1 , x2 e (0, +伪) ,使得g (x1 ) = g (x2 ) ,
不妨设x1 < x2 ,即x1 e (|(0, , x2 e , +伪 ,则
1- x1 e , 1 , .................... 11 分
设G(x) = g (x) - g (1 - x) , x e(|(0, ,
则G,(x ) = g,(x ) + g,(1 - x ) = 4
1 1
x 1 - x
1
x (1 - x ) ,
................. 13 分
当x e(|(0, 时, e (4, +伪) ,可知G, (x) < 0在(|(0, 上恒成立,
则G(x)在(|(0, 内单调递减,
可得G(x) > G = 0 ,
即g (x) > g (1- x), x = (|(0, , ................... 15 分
又因为x1 = (|(0, , x2 = , +伪 ,1- x1 = , 1 ,则g (x1 ) = g (x2 ) > g (1 - x1 ) ,
且g (x) 在 , +伪上单调递增,可得x2 > 1- x1 ,
即x1 + x2 >1 . ...17 分
同课章节目录
