湘教版初中数学导学案七年级上册·第4章 图形的认识
文档属性
| 名称 | 湘教版初中数学导学案七年级上册·第4章 图形的认识 |

|
|
| 格式 | zip | ||
| 文件大小 | 881.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-10-03 00:00:00 | ||
图片预览


文档简介
( http: / / www.21cnjy.com )
第4章 图形的认识
4.1 几何图形
1.能从现实物体中抽象出几何图形.
2.能准确区分立体图形与平面图形.
3.体验平面图形与立体图形之间的相互转化,明确二者之间的关系.
一、 新知探究
初中阶段,把数学大体分为代数学和几何学,前三章我们学习的有理数、代数式以及方程都属于代数的范畴,那么什么是几何呢,让我们一起来感受一下吧!
阅读教材第112~114页的内容,自主探究,回答下列问题:
1.你认为几何主要研究的是什么 与代数相比它有哪些显著的特征
2.什么是几何图形,你能举例说明吗
3.几何图形分为哪两类 请用自己的话分别加以描述,举例说明.
4.你能找出立体图形与平面图形之间的区别和联系吗 二者能互相转化吗
5.请画出如图所示正方体的的展开图,至少画出两种不同的展开图.
( http: / / www.21cnjy.com )
二、 基础演练
根据以上的探究,自主解决下列问题,并与小组成员交流分享你的学习成果:
1.请找出下面图案中所有的几何图形.
( http: / / www.21cnjy.com )
2.请分别将下列四个图形的名称写在横线上.
( http: / / www.21cnjy.com )
3.下面的图形中是平面图形的是 ( )
4.下图可以是一个正方体的平面展开图的是 ( )
三、 综合提升
先尝试独立解决,再与小组成员合作交流,解决下列问题:
1.从下面的图形中,你能抽象出哪些立体图形和平面图形.
( http: / / www.21cnjy.com )
2.将直角三角形绕它一条直角边旋转一周所成的图形是 ,将长方形形绕它一条边旋转一周所成的图形是 .
1.写出下列图形的名称.
( http: / / www.21cnjy.com )
① ②
③ ④
⑤
2.下列图形中,平面图形有 ,空间图形有 .
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
3.将圆绕它一条直径旋转一周所成的图形是 .
本课时主要学习了哪些知识与方法 有何收获和感悟 还有哪些疑惑
欧拉公式
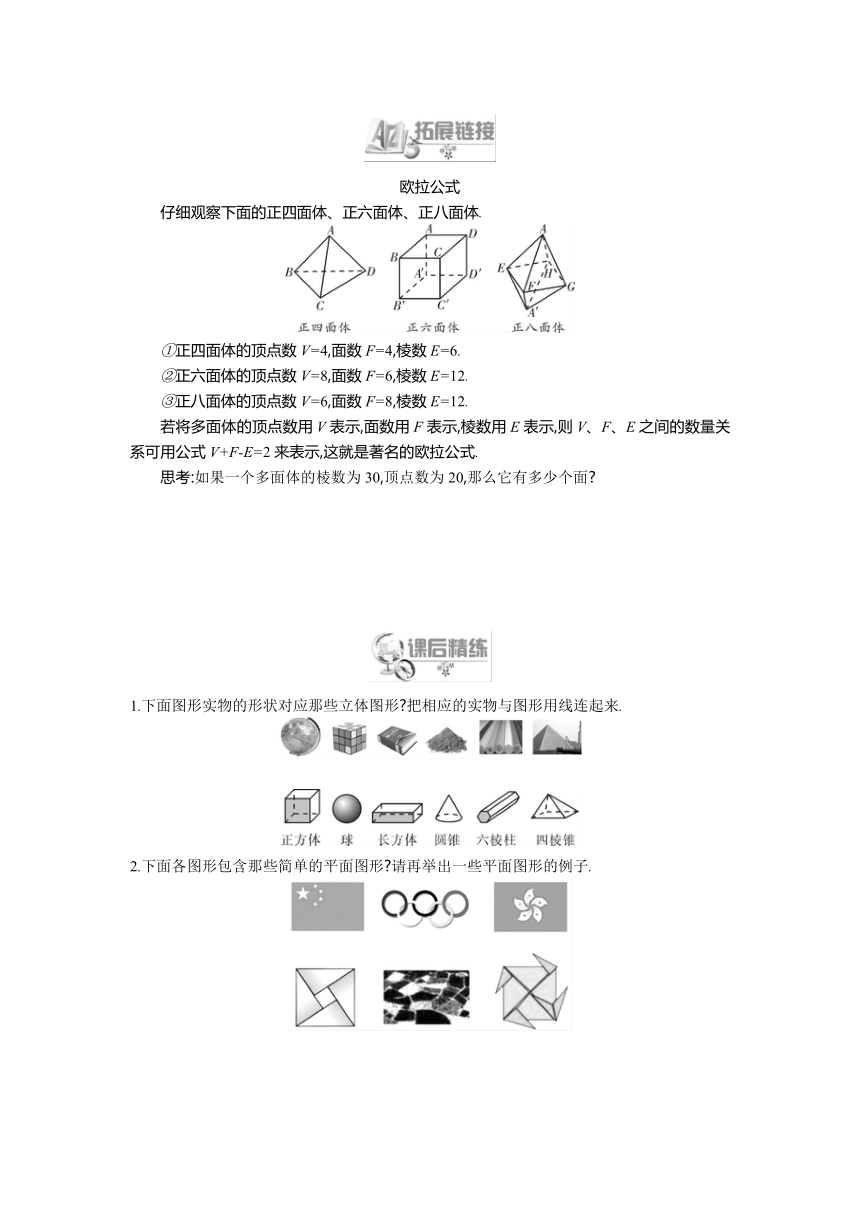
仔细观察下面的正四面体、正六面体、正八面体.
( http: / / www.21cnjy.com )
①正四面体的顶点数V=4,面数F=4,棱数E=6.
②正六面体的顶点数V=8,面数F=6,棱数E=12.
③正八面体的顶点数V=6,面数F=8,棱数E=12.
若将多面体的顶点数用V表示,面数用F表示,棱数用E表示,则V、F、E之间的数量关系可用公式V+F-E=2来表示,这就是著名的欧拉公式.
思考:如果一个多面体的棱数为30,顶点数为20,那么它有多少个面
1.下面图形实物的形状对应那些立体图形 把相应的实物与图形用线连起来.
2.下面各图形包含那些简单的平面图形 请再举出一些平面图形的例子.
( http: / / www.21cnjy.com )
3.下面各立方图形的表面包含哪些平面图形 试指出这些平面图形在立体图形中的位置.
4.2 线段、射线、直线(1)
1.能从现实情境中抽象出线段、射线、直线的概念,并掌握它们的表示方法.
2.理解点与直线的位置关系,并能描述点与直线的位置关系.
3.掌握“两点确定一条直线”的基本事实.
一、 新知探究
阅读教材第117~119页的内容,自主探究,回答下列问题:
1.结合对教材中线段、射线、直线的概念的理解,可以从下面实物图中能抽象出什么图形
(1)
(2)
(3)
2.点与直线有怎样的位置关系,请画图说明.
3.要把一根木条固定在墙上,至少需要几颗钉子 从这里你可以得出怎样的基本事实
二、 基础演练
根据以上的探究,自主解决下列问题,并与小组成员交流分享你的学习成果:
1.试一试,将线段、射线和直线的相关知识总结在下表中:
名称 图形 表示方法 端点个数 长度是否可度量
线段
射线
直线
小结:线段或直线可用 个大写字母或 个小写字母来表示;射线只能用 表示,且端点的字母一定要放在前面.
2.如图,下列说法不正确的是 ( )
A.直线AB与直线BA是同一直线
B.射线OB与射线OA是同一条射线
C.射线OA与射线AB是同一条射线
D.线段AB与线段BA是同一条线段
3.下列说法中正确的是 ( )
A.画一条3 cm长的直线
B.画一条3 cm长的射线
C.画一条3 cm长的线段
D.在直线、射线、线段中,直线最长
4.按照下列语句分别画出图形.
(1)点P在直线l外;
(2)以O为端点的三条射线OA,OB,OC;
(3)点C在线段AB上.
三、 综合提升
先尝试独立解决,再与小组成员合作交流,解决下列问题:
在平面内任意四个点所确定的直线可能有多少条 请在下面画出你能想到的可能情况.
1.下列说法中错误的是 ( )
A. A,B两点之间的距离为3 cm
B. A,B两点之间的距离为线段AB的长度
C. 线段AB的中点C到A,B两点的距离相等
D. A,B两点之间的距离是线段AB
2.下列说法中,正确的个数有 ( )
①射线AB和射线BA是同一条射线;
②延长射线MN到C;
③延长线段MN到A使NA=2MN;
④连结两点的线段叫做两点间的距离.
A. 1 B. 2
C. 3 D. 4
3.在直线上取A,B,C三点,使得AB=9 cm,BC=5 cm,如果O是线段AC的中点,则线段OA的长为 cm.
本课时主要学习了哪些知识与方法 有何收获和感悟 还有哪些疑惑
在测量中怎样定点定线
1.定点:在测量时,常要先定出一些点.如 ( http: / / www.21cnjy.com )测量一条渠道,就要先标定出渠道的起点、终点以及表示渠道走向的点;测量一个地区的地形图,要先在这个地区范围内选定一批作为依据的观测点;架设电线时,要先选定电线杆的位置.定点,就是在地面上标出测量工作所必需的点.在实际操作中,常用木桩或标杆来定点.有时,为节约开支,也可用竹签代替木桩来定点.对于永久性的点位,要用石桩或水泥桩做标志,也可以在坚固的岩石或水泥建筑物上用油漆绘出标志来标定.
2.定直线:我们知道两点确定一条直线,但为 ( http: / / www.21cnjy.com )了测量工作的方便以及工程上的需要,常常要在一直线上插入一些标杆,以明确表示直线的位置,这在测量中叫做定线.定线可用仪器或用目测来进行.
1.按下列语句分别画出图形.
(1)过一点P画直线AB.
(2)直线m,n,l相交于点P.
(3)线段AB与线段CD相交于点O.
(4)A,B,C是直线l上三点,且点C在点A与点B之间.
2.如下图所示,以O为端点的射线有 条,图中共有 条线段;图中共有 条直线.
( http: / / www.21cnjy.com )
4.2 线段、射线、直线(2)
1.会比较两条线段的长短,理解线段的和、差的意义.
2.掌握“两点之间线段最短”的基本事实.
3.了解尺规作图,会用尺规作两线段的和与差.
4.理解线段中点的意义,会准确用数学语言书写有关线段中点的计算问题.
一、 新知探究
阅读教材第119~121页的内容,自主探究,回答下列问题:
1.在教材第119页“做一做”中,介绍了哪两种比较两条线段大小的方法 分别是哪两种
2.在教材第120页“动脑筋”中得到了“两点之间线段最短”的基本事实,请你举例说明.
3.在教材第121页的例1中,介绍了一种非常重要的做图方法——尺规作图,这里对“尺”和“规”各有什么要求 在作图中它们分别有怎样的作用
4.在教材第121页中介绍了线段的中点的概念,请你用几何语言进行描述,在实际生活中,你能找出线段中点的应用吗
二、 基础演练
根据以上的探究,自主解决下列问题,并与小组成员交流分享你的学习成果:
1.不看教材,完成下列表格.
为了比较线段AB,CD的长短,将线段AB移到CD上,使点A与点C重合,点B与点D都在点C的同侧,可能出现的情形如下表:
图形 线段AB与CD的关系 记作
2.已知线段AB的长为10 cm,C为AB的中点,则AC= ,BC= .
3.如图所示,线段a,b,且a>b.用圆规和直尺画线段:
(1)a+b;
(2)a-b.
4.如图,直线l是一条近似平直的河流,A, ( http: / / www.21cnjy.com )B是河两岸的两个城市.现要在A,B两城市之间建一个码头C,使两城市到码头的距离之和最小(河宽不计).请你找出码头的位置.
( http: / / www.21cnjy.com )
5.如图,线段AB=6 cm,点C是AB的中点,点D是AC的中点,求线段AC,AD的长.
学法指导:书写格式请按照新知探究中规范的数学语言进行.
三、 综合提升
先尝试独立解决,再与小组成员合作交流,解决下列问题:
1.若A,B,C三点在同一条直线上,当AB=5 cm,AC=3 cm时,B,C两点间的距离是 .
2.若A,B,C三点在同一条直线上,当AB=5 cm,AC=3 cm时,B,C两点间最长的距离是 .
学法指导:书写格式请按照新知探究中规范的数学语言进行.
1.如图所示,已知AB=CD,则AC与BD的大小关系是 ( )
A. AC>BD B. ACC. AC=BD D.不确定
2.如图所示,已知直线上有四点A,B,C,D,AD= +CD=AB- ,AD+CB-AB= .
3.如下图所示,已知C是AB的中点,D是BC的中点,则下列等式不成立的是 ( )
A. CD=AC-DB B. CD=AD-BC
C. CD=AB-BD D. CD=AB
本课时主要学习了哪些知识与方法 有何收获和感悟 还有哪些疑惑
最大与最小的长度单位
中国有句俗语“差之毫厘,失之千里”,因此,很多人以为,毫、厘是最小的长度单位.
随着人类对宏观世界认识的不 ( http: / / www.21cnjy.com )断扩大,对微观世界的认识也在不断深入;大单位越来越大,小单位越来越小.在天文学中常用的最大长度单位是光年(Light year),是光(每秒299 792.459公里)在一年(365天)里走的距离;最小的长度单位是“埃”,一亿分之一(10-8)厘米.
后来又出现了比埃更小的长度单位,即at ( http: / / www.21cnjy.com )to-meter.1个atto-meter是十的十六次方分之一(10-16)厘米.从1960年开始,度量时间的最短单位称为nano-second,为十亿分之一秒.光线在1个nano-second里,只能走30厘米.
还有比光年更大的单为.太阳以银河为 ( http: / / www.21cnjy.com )中心绕一周,通常称为一个宇宙年,约等于2亿5千万年.但是,最大的长度单位是印度教记年上的“卡巴尔”:一个卡巴尔等于43亿2千万年,或19个宇宙年.
1.如下图,A,B,C,D四点在一条直线上,则:
(1)BD+CD= ;
(2)AB-AC= ;
(3)AB-AC-BD= .
2.当AB=5 cm,BC=3 cm时,A,C两点间的距离是 ( )
A. 2 cm B. 7 cm
C. 8 cm D. 2 cm或8 cm
3.如图,线段AB=1.8 cm,延长AB至点C,使得BC=3AB,D为BC的中点,则B,D两点间的距离是多少
4.如图所示,点C为线段AB上的一点,点D是线段AC的中点,点E是线段CB的中点,AB=9 cm,AC=5 cm.求:
(1)AD的长;
(2)DE的长.
5.如图,已知线段a,b,作一条线段使它等于a+2b.(只要求作出图形,不要求写作法.)
4.3 角
4.3.1 角与角的大小比较
1.理解角、平角、周角的概念,掌握角的几种表示方法.
2.会用度量法和叠合法比较两个角的大小,丰富对角的大小的关系的认识.
3.理解角的平分线的概念,会用角的平分线解决角的计算问题.
一、 新知探究
阅读教材第123~125页的内容,自主探究,回答下列问题:
1.在教材第123页中,谈到了角的两个概念,我们把其中的一种理解为“静态概念”,另外一种理解为“动态概念”,请你分别进行描述.
①静态概念:
②动态概念:
2.在前面,我们知道线段有长度,同样地角也有大小.那么角的大小是由什么决定的呢
3.线段、射线、直线都有自己的表示方法,那么如何表示一个角呢 请你结合教材第124页的内容进行总结.(温馨提示:共有四种)
4.既然角有大小,那么如何比较两个角的大小呢 请类比线段大小的比较方法,总结两种角的大小的比较方法.
5.教材中引入了角平分线的概念,你能用几何语言进行描述吗
二、 基础演练
根据以上的探究,自主解决下列问题,并与小组成员交流分享你的学习成果:
1.先将∠DEF移动,使顶点E与∠AOB的顶点O重合,且边EF和边OA重合,则边DE,OB都在OA的同侧,这时可能出现的情形如下表:
情形 图形 ∠AOB和∠DEF的关系
ED与BO重合
ED落在∠AOB内部
ED落在∠AOB外部
2.如图,射线OC是∠AOB的平分线,则:
∠AOC= ;∠AOC= ;
∠AOB=2 =2 .
3.如图,下面表示角的方法不正确的是 ( )
( http: / / www.21cnjy.com )
A.∠A
B.∠D
C.∠OCB
D.∠B
4.下列两个图中分别有几个角 请用适当的方式将这些角表示出来.
三、 综合提升
先尝试独立解决,再与小组成员合作交流,解决下列问题:
1.如图,射线OC平分∠BOD,OB平分∠AOC,以下结论中正确的是 ( )
①∠COD=∠COB=∠AOB;
( http: / / www.21cnjy.com )
②∠COD=∠AOC;
③∠BOD=2∠AOB;
④∠AOD=2∠BOD.
A. ①②③ B. ②③④
C. ①③④ D. ①②③④
2.如图,OA、OB、OC、OD、OE是经过点O的5条射线,问图中共有几个角 分别写出来
( http: / / www.21cnjy.com )
1.下列四个图形中,能同时用∠1,∠ABC,∠B三种方法表示同一个角的图形是 ( )
2.下列各图中,角的射线依次增加,请数一数各图中有几个角
( http: / / www.21cnjy.com )
(1)如果一个角内部有8条射线,那么该图中有 个角.
(2)如果一个角内部有n条射线,那么该图中有 个角.
本课时主要学习了哪些知识与方法 有何收获和感悟 还有哪些疑惑
3根指挥棒和12个直角
英国发明家瓦特(1736—1819 ( http: / / www.21cnjy.com ))获得了蒸汽机专利后,从一个大学实验员一跃为波士顿─瓦特公司的老板,还成为英国皇家学会的会员,引起了许多旧贵族的不满.据说,在一次皇家音乐会上,有个贵族故意嘲讽地对瓦特说:“乐队指挥手里拿的东西在物理学家眼里仅仅是根棒子而已.”瓦特回答道:“是的,那的确是根棒子,但是我可以用这样3根棒子组成12个直角,而你却不能做到.”那个贵族不服气地用3根指挥棒在桌上摆来摆去,可始终无法摆出12个直角.
你能拼出12个直角吗 你自己先试试看!
1.下列说法错误的是 ( )
A.∠AOB的顶点是O
B.∠AOB的边是两条射线
C.∠AOB与∠BOA表示同一个角
D.射线BO、射线AO分别是∠AOB的边
2.已知O是直线AB上一点,OC是一条射线,则∠AOC与∠BOC的关系是 ( )
A.∠AOC一定大于∠BOC
B.∠AOC一定小于∠BOC
C.∠AOC一定等于∠BOC
D.∠AOC可能大于、等于或小于∠BOC
3.如图,OC平分∠AOB,OD平分∠COB ( http: / / www.21cnjy.com ),∠AOB=x,则∠AOC= ,∠COD= ,∠AOD= + = .
( http: / / www.21cnjy.com )
4.3.2 角的度量与计算(1)
1.理解角的度量单位度、分、秒.
2.会进行角度的简单换算以及角的和、差计算.
一、 新知探究
阅读教材第126、127页的内容,自主探究,回答下列问题:
我们在测量长度时,要用到长 ( http: / / www.21cnjy.com )度单位如:千米、米、厘米、分米、毫米等;在测量重量时,要用到重量单位如:吨、千克、克等;在描述时间时,要用到时间单位如:年、月、日、时、分、秒.
1.每种单位之间都可以互 ( http: / / www.21cnjy.com )相换算,如:1千米=1 000 米,这里我们不妨把“千米”称为“大单位”,把“米”称为“小单位”,那么从“大单位”到“小单位”是如何换算的呢 请根据长度单位的换算关系写出你的理解和做法.
2.要度量角的大小就需要角的度量单位,请认真阅读教材,描述1°的概念.
3.角度单位的换算与时间单位的时、分、秒之间的换算是一致的,因此角度的基本度量单位之间的换算也是60进制,请你写出角度单位的换算关系.
4. 180度以内的角,可以按照角的大小分为哪三种角,请分别画图说明.
二、 基础演练
根据以上的探究,自主解决下列问题,并与小组成员交流分享你的学习成果:
1.两个锐角的和 ( )
A.一定为锐角
B.一定为钝角
C.一定为直角
D.可能是锐角或钝角或直角
2.若∠1=50°5',∠2=50.5°,则∠1和∠2的大小关系是 ( )
A.∠1=∠2 B.∠1>∠2
C.∠1<∠2 D.无法确定
3.阅读教材第126页例1、例2,完成下列题目.
(1)用度、分、秒表示32.36°;
(2)用度表示14°48'54″.
4.阅读教材第127页例3,仿做下题.
(1)77°42'+34°45';
(2)180°-56°23'18″.
三、 综合提升
先尝试独立解决,再与小组成员合作交流,解决下列问题:
1.观察钟面,1小时时针转 度;1分钟分针转 度,时针转 度.
2.求下列时刻时针与分针所成的角,并探索规律.
(1)8点整;
(2)6点30分;
(3)5点54分.
计算:
(1)用度、分、秒表示30.26°;
(2)用度表示35°25'48″;
(3)20°26'+35°54';
(4)90°-43°18'.
本课时主要学习了哪些知识与方法 有何收获和感悟 还有哪些疑惑
用数写的格言
1.王菊珍的百分数
我国科学家王菊珍对待实验失败有句格言,叫做“干下去还有50%成功的希望,不干便是100%的失败.”
2.托尔斯泰的分数
俄国大文豪托尔斯泰在谈到人的评价时,把 ( http: / / www.21cnjy.com )人比作一个分数.他说:“一个人就好像一个分数,他的实际才能好比分子,而他对自己的估价好比分母.分母越大,则分数的值就越小.”
3.雷巴柯夫的常数与变数
俄国历史学家雷巴柯夫在利用时间方面是这 ( http: / / www.21cnjy.com )样说的:“时间是个常数,但对勤奋者来说,是个‘变数’.用‘分’来计算时间的人比用‘小时’来计算时间的人时间多59倍.”
1.已知OC平分∠AOB,若∠BOC=29°34',则∠AOB= .
2.(1)用度、分、秒表示39.33°;
(2)用度表示65°25'12″.
3.计算:
(1)49°38'+66°22'26″;
(2)167°13'-79°48'35″.
4.已知钟表现在时刻为2:30,此时时针和分针所夹角的度数是多少
4.3.2 角的度量与计算(2)
1.知道余角、补角的概念,并会求一个角的余角或补角.
2.理解余角、补角的性质,并能通过它们的性质进行角的运算.
3.体会几何问题从观察、测量、探究向证明的转变.
一、 新知探究
通过阅读教材第128、129页,然后根据你对教材的理解,回答下列问题:
1.如果两个角互为余角,那么对这两个角的大小有怎样的要求,对它们的位置有要求吗
2.如果两个角互为补角,那么对这两个角的大小有怎样的要求,对它们的位置有要求吗
3.教材第128页的“探究”中谈到了“等量代换”的概念,你能用自己的话进行描述吗
4.教材第128页的“探究”中得出结论“同角(或等角)的补角相等”,你理解这句话的含义吗,试结合下图用几何语言进行描述.
5.“同角(或等角)的余角相等”,你理解这句话的含义吗,请结合下图用几何语言进行描述.
( http: / / www.21cnjy.com )
二、 基础演练
根据以上的探究,自主解决下列问题,并与小组成员交流分享你的学习成果:
1.(1)58°的余角是 ,补角是 ;
(2)105°25'的补角是 ;
(3)36°18'47″的余角是 ;
2.已知∠1和∠2互余,∠3和∠2互补,且有∠3=143°,则∠1= .
3.一个角的余角和补角也互为补角,这个角是 ( )
A. 30° B. 75°
C. 45° D. 15°
4.已知一个角比它的余角小15°,则这个角的补角是多少度
三、 综合提升
先尝试独立解决,再与小组成员合作交流,解决下列问题:
1.已知∠A=42°,则它的余角等于 ,补角等于 ,补角与余角的差等于 .
2.如图,O为直线AB上的一点,OM平分∠AOC,ON平分∠BOC,则图中互余的角共有 ( )
A. 1对
B. 2对
C. 3对
D. 4对
3.∠A的余角与∠A的补角互为补角,那么2∠A是 ( )
A.直角 B.锐角
C.钝角 D.以上三种都有可能
4.如图,已知AC为一条直线,O为直线AC上一点,且∠DOB=∠AOB,∠BOE=∠BOC,∠DOB与∠BOE互余,求∠AOB和∠BOC的度数.
1.一个角的补角是36°35',这个角的度数是 .
2.如图,点O在直线AB上,OC为射线,∠1比∠2的3倍少10°,则∠1和∠2的度数分别为 ( )
A.∠1=80°,∠2=100°
B.∠1=100°,∠2=80°
C.∠1=47.5°,∠2=132.5°
D.∠1=132.5°,∠2=47.5°
3.一个角的余角比它的补角的还少20°,求这个角的度数
本课时主要学习了哪些知识与方法 有何收获和感悟 还有哪些疑惑
数学谜语
(1)上午不上午,下午不下午,两针合一处,太阳猛似虎.(打一时刻)
(2)待命出发.(打一数学符号)
(3)一减一不是0.(打一数字)
(4)剃头(打一数学计算方法)
(5)停战(打一数学名称)
1.一个角的余角是53°47'25″,则这个角的补角的度数是 .
2.一个角等于它的补角的5倍,那么这个角的补角的余角是 ( )
A. 30° B. 60°
C. 45° D. 150°
3.已知一个角的补角是它余角的4倍,求这个角的度数.
4.如图,∠AOB=114°,OF是∠AOB的平分线,∠1与∠2互余,求∠1的度数.
第4章 图形的认识
4.1 几何图形
1.能从现实物体中抽象出几何图形.
2.能准确区分立体图形与平面图形.
3.体验平面图形与立体图形之间的相互转化,明确二者之间的关系.
一、 新知探究
初中阶段,把数学大体分为代数学和几何学,前三章我们学习的有理数、代数式以及方程都属于代数的范畴,那么什么是几何呢,让我们一起来感受一下吧!
阅读教材第112~114页的内容,自主探究,回答下列问题:
1.你认为几何主要研究的是什么 与代数相比它有哪些显著的特征
2.什么是几何图形,你能举例说明吗
3.几何图形分为哪两类 请用自己的话分别加以描述,举例说明.
4.你能找出立体图形与平面图形之间的区别和联系吗 二者能互相转化吗
5.请画出如图所示正方体的的展开图,至少画出两种不同的展开图.
( http: / / www.21cnjy.com )
二、 基础演练
根据以上的探究,自主解决下列问题,并与小组成员交流分享你的学习成果:
1.请找出下面图案中所有的几何图形.
( http: / / www.21cnjy.com )
2.请分别将下列四个图形的名称写在横线上.
( http: / / www.21cnjy.com )
3.下面的图形中是平面图形的是 ( )
4.下图可以是一个正方体的平面展开图的是 ( )
三、 综合提升
先尝试独立解决,再与小组成员合作交流,解决下列问题:
1.从下面的图形中,你能抽象出哪些立体图形和平面图形.
( http: / / www.21cnjy.com )
2.将直角三角形绕它一条直角边旋转一周所成的图形是 ,将长方形形绕它一条边旋转一周所成的图形是 .
1.写出下列图形的名称.
( http: / / www.21cnjy.com )
① ②
③ ④
⑤
2.下列图形中,平面图形有 ,空间图形有 .
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
3.将圆绕它一条直径旋转一周所成的图形是 .
本课时主要学习了哪些知识与方法 有何收获和感悟 还有哪些疑惑
欧拉公式
仔细观察下面的正四面体、正六面体、正八面体.
( http: / / www.21cnjy.com )
①正四面体的顶点数V=4,面数F=4,棱数E=6.
②正六面体的顶点数V=8,面数F=6,棱数E=12.
③正八面体的顶点数V=6,面数F=8,棱数E=12.
若将多面体的顶点数用V表示,面数用F表示,棱数用E表示,则V、F、E之间的数量关系可用公式V+F-E=2来表示,这就是著名的欧拉公式.
思考:如果一个多面体的棱数为30,顶点数为20,那么它有多少个面
1.下面图形实物的形状对应那些立体图形 把相应的实物与图形用线连起来.
2.下面各图形包含那些简单的平面图形 请再举出一些平面图形的例子.
( http: / / www.21cnjy.com )
3.下面各立方图形的表面包含哪些平面图形 试指出这些平面图形在立体图形中的位置.
4.2 线段、射线、直线(1)
1.能从现实情境中抽象出线段、射线、直线的概念,并掌握它们的表示方法.
2.理解点与直线的位置关系,并能描述点与直线的位置关系.
3.掌握“两点确定一条直线”的基本事实.
一、 新知探究
阅读教材第117~119页的内容,自主探究,回答下列问题:
1.结合对教材中线段、射线、直线的概念的理解,可以从下面实物图中能抽象出什么图形
(1)
(2)
(3)
2.点与直线有怎样的位置关系,请画图说明.
3.要把一根木条固定在墙上,至少需要几颗钉子 从这里你可以得出怎样的基本事实
二、 基础演练
根据以上的探究,自主解决下列问题,并与小组成员交流分享你的学习成果:
1.试一试,将线段、射线和直线的相关知识总结在下表中:
名称 图形 表示方法 端点个数 长度是否可度量
线段
射线
直线
小结:线段或直线可用 个大写字母或 个小写字母来表示;射线只能用 表示,且端点的字母一定要放在前面.
2.如图,下列说法不正确的是 ( )
A.直线AB与直线BA是同一直线
B.射线OB与射线OA是同一条射线
C.射线OA与射线AB是同一条射线
D.线段AB与线段BA是同一条线段
3.下列说法中正确的是 ( )
A.画一条3 cm长的直线
B.画一条3 cm长的射线
C.画一条3 cm长的线段
D.在直线、射线、线段中,直线最长
4.按照下列语句分别画出图形.
(1)点P在直线l外;
(2)以O为端点的三条射线OA,OB,OC;
(3)点C在线段AB上.
三、 综合提升
先尝试独立解决,再与小组成员合作交流,解决下列问题:
在平面内任意四个点所确定的直线可能有多少条 请在下面画出你能想到的可能情况.
1.下列说法中错误的是 ( )
A. A,B两点之间的距离为3 cm
B. A,B两点之间的距离为线段AB的长度
C. 线段AB的中点C到A,B两点的距离相等
D. A,B两点之间的距离是线段AB
2.下列说法中,正确的个数有 ( )
①射线AB和射线BA是同一条射线;
②延长射线MN到C;
③延长线段MN到A使NA=2MN;
④连结两点的线段叫做两点间的距离.
A. 1 B. 2
C. 3 D. 4
3.在直线上取A,B,C三点,使得AB=9 cm,BC=5 cm,如果O是线段AC的中点,则线段OA的长为 cm.
本课时主要学习了哪些知识与方法 有何收获和感悟 还有哪些疑惑
在测量中怎样定点定线
1.定点:在测量时,常要先定出一些点.如 ( http: / / www.21cnjy.com )测量一条渠道,就要先标定出渠道的起点、终点以及表示渠道走向的点;测量一个地区的地形图,要先在这个地区范围内选定一批作为依据的观测点;架设电线时,要先选定电线杆的位置.定点,就是在地面上标出测量工作所必需的点.在实际操作中,常用木桩或标杆来定点.有时,为节约开支,也可用竹签代替木桩来定点.对于永久性的点位,要用石桩或水泥桩做标志,也可以在坚固的岩石或水泥建筑物上用油漆绘出标志来标定.
2.定直线:我们知道两点确定一条直线,但为 ( http: / / www.21cnjy.com )了测量工作的方便以及工程上的需要,常常要在一直线上插入一些标杆,以明确表示直线的位置,这在测量中叫做定线.定线可用仪器或用目测来进行.
1.按下列语句分别画出图形.
(1)过一点P画直线AB.
(2)直线m,n,l相交于点P.
(3)线段AB与线段CD相交于点O.
(4)A,B,C是直线l上三点,且点C在点A与点B之间.
2.如下图所示,以O为端点的射线有 条,图中共有 条线段;图中共有 条直线.
( http: / / www.21cnjy.com )
4.2 线段、射线、直线(2)
1.会比较两条线段的长短,理解线段的和、差的意义.
2.掌握“两点之间线段最短”的基本事实.
3.了解尺规作图,会用尺规作两线段的和与差.
4.理解线段中点的意义,会准确用数学语言书写有关线段中点的计算问题.
一、 新知探究
阅读教材第119~121页的内容,自主探究,回答下列问题:
1.在教材第119页“做一做”中,介绍了哪两种比较两条线段大小的方法 分别是哪两种
2.在教材第120页“动脑筋”中得到了“两点之间线段最短”的基本事实,请你举例说明.
3.在教材第121页的例1中,介绍了一种非常重要的做图方法——尺规作图,这里对“尺”和“规”各有什么要求 在作图中它们分别有怎样的作用
4.在教材第121页中介绍了线段的中点的概念,请你用几何语言进行描述,在实际生活中,你能找出线段中点的应用吗
二、 基础演练
根据以上的探究,自主解决下列问题,并与小组成员交流分享你的学习成果:
1.不看教材,完成下列表格.
为了比较线段AB,CD的长短,将线段AB移到CD上,使点A与点C重合,点B与点D都在点C的同侧,可能出现的情形如下表:
图形 线段AB与CD的关系 记作
2.已知线段AB的长为10 cm,C为AB的中点,则AC= ,BC= .
3.如图所示,线段a,b,且a>b.用圆规和直尺画线段:
(1)a+b;
(2)a-b.
4.如图,直线l是一条近似平直的河流,A, ( http: / / www.21cnjy.com )B是河两岸的两个城市.现要在A,B两城市之间建一个码头C,使两城市到码头的距离之和最小(河宽不计).请你找出码头的位置.
( http: / / www.21cnjy.com )
5.如图,线段AB=6 cm,点C是AB的中点,点D是AC的中点,求线段AC,AD的长.
学法指导:书写格式请按照新知探究中规范的数学语言进行.
三、 综合提升
先尝试独立解决,再与小组成员合作交流,解决下列问题:
1.若A,B,C三点在同一条直线上,当AB=5 cm,AC=3 cm时,B,C两点间的距离是 .
2.若A,B,C三点在同一条直线上,当AB=5 cm,AC=3 cm时,B,C两点间最长的距离是 .
学法指导:书写格式请按照新知探究中规范的数学语言进行.
1.如图所示,已知AB=CD,则AC与BD的大小关系是 ( )
A. AC>BD B. AC
2.如图所示,已知直线上有四点A,B,C,D,AD= +CD=AB- ,AD+CB-AB= .
3.如下图所示,已知C是AB的中点,D是BC的中点,则下列等式不成立的是 ( )
A. CD=AC-DB B. CD=AD-BC
C. CD=AB-BD D. CD=AB
本课时主要学习了哪些知识与方法 有何收获和感悟 还有哪些疑惑
最大与最小的长度单位
中国有句俗语“差之毫厘,失之千里”,因此,很多人以为,毫、厘是最小的长度单位.
随着人类对宏观世界认识的不 ( http: / / www.21cnjy.com )断扩大,对微观世界的认识也在不断深入;大单位越来越大,小单位越来越小.在天文学中常用的最大长度单位是光年(Light year),是光(每秒299 792.459公里)在一年(365天)里走的距离;最小的长度单位是“埃”,一亿分之一(10-8)厘米.
后来又出现了比埃更小的长度单位,即at ( http: / / www.21cnjy.com )to-meter.1个atto-meter是十的十六次方分之一(10-16)厘米.从1960年开始,度量时间的最短单位称为nano-second,为十亿分之一秒.光线在1个nano-second里,只能走30厘米.
还有比光年更大的单为.太阳以银河为 ( http: / / www.21cnjy.com )中心绕一周,通常称为一个宇宙年,约等于2亿5千万年.但是,最大的长度单位是印度教记年上的“卡巴尔”:一个卡巴尔等于43亿2千万年,或19个宇宙年.
1.如下图,A,B,C,D四点在一条直线上,则:
(1)BD+CD= ;
(2)AB-AC= ;
(3)AB-AC-BD= .
2.当AB=5 cm,BC=3 cm时,A,C两点间的距离是 ( )
A. 2 cm B. 7 cm
C. 8 cm D. 2 cm或8 cm
3.如图,线段AB=1.8 cm,延长AB至点C,使得BC=3AB,D为BC的中点,则B,D两点间的距离是多少
4.如图所示,点C为线段AB上的一点,点D是线段AC的中点,点E是线段CB的中点,AB=9 cm,AC=5 cm.求:
(1)AD的长;
(2)DE的长.
5.如图,已知线段a,b,作一条线段使它等于a+2b.(只要求作出图形,不要求写作法.)
4.3 角
4.3.1 角与角的大小比较
1.理解角、平角、周角的概念,掌握角的几种表示方法.
2.会用度量法和叠合法比较两个角的大小,丰富对角的大小的关系的认识.
3.理解角的平分线的概念,会用角的平分线解决角的计算问题.
一、 新知探究
阅读教材第123~125页的内容,自主探究,回答下列问题:
1.在教材第123页中,谈到了角的两个概念,我们把其中的一种理解为“静态概念”,另外一种理解为“动态概念”,请你分别进行描述.
①静态概念:
②动态概念:
2.在前面,我们知道线段有长度,同样地角也有大小.那么角的大小是由什么决定的呢
3.线段、射线、直线都有自己的表示方法,那么如何表示一个角呢 请你结合教材第124页的内容进行总结.(温馨提示:共有四种)
4.既然角有大小,那么如何比较两个角的大小呢 请类比线段大小的比较方法,总结两种角的大小的比较方法.
5.教材中引入了角平分线的概念,你能用几何语言进行描述吗
二、 基础演练
根据以上的探究,自主解决下列问题,并与小组成员交流分享你的学习成果:
1.先将∠DEF移动,使顶点E与∠AOB的顶点O重合,且边EF和边OA重合,则边DE,OB都在OA的同侧,这时可能出现的情形如下表:
情形 图形 ∠AOB和∠DEF的关系
ED与BO重合
ED落在∠AOB内部
ED落在∠AOB外部
2.如图,射线OC是∠AOB的平分线,则:
∠AOC= ;∠AOC= ;
∠AOB=2 =2 .
3.如图,下面表示角的方法不正确的是 ( )
( http: / / www.21cnjy.com )
A.∠A
B.∠D
C.∠OCB
D.∠B
4.下列两个图中分别有几个角 请用适当的方式将这些角表示出来.
三、 综合提升
先尝试独立解决,再与小组成员合作交流,解决下列问题:
1.如图,射线OC平分∠BOD,OB平分∠AOC,以下结论中正确的是 ( )
①∠COD=∠COB=∠AOB;
( http: / / www.21cnjy.com )
②∠COD=∠AOC;
③∠BOD=2∠AOB;
④∠AOD=2∠BOD.
A. ①②③ B. ②③④
C. ①③④ D. ①②③④
2.如图,OA、OB、OC、OD、OE是经过点O的5条射线,问图中共有几个角 分别写出来
( http: / / www.21cnjy.com )
1.下列四个图形中,能同时用∠1,∠ABC,∠B三种方法表示同一个角的图形是 ( )
2.下列各图中,角的射线依次增加,请数一数各图中有几个角
( http: / / www.21cnjy.com )
(1)如果一个角内部有8条射线,那么该图中有 个角.
(2)如果一个角内部有n条射线,那么该图中有 个角.
本课时主要学习了哪些知识与方法 有何收获和感悟 还有哪些疑惑
3根指挥棒和12个直角
英国发明家瓦特(1736—1819 ( http: / / www.21cnjy.com ))获得了蒸汽机专利后,从一个大学实验员一跃为波士顿─瓦特公司的老板,还成为英国皇家学会的会员,引起了许多旧贵族的不满.据说,在一次皇家音乐会上,有个贵族故意嘲讽地对瓦特说:“乐队指挥手里拿的东西在物理学家眼里仅仅是根棒子而已.”瓦特回答道:“是的,那的确是根棒子,但是我可以用这样3根棒子组成12个直角,而你却不能做到.”那个贵族不服气地用3根指挥棒在桌上摆来摆去,可始终无法摆出12个直角.
你能拼出12个直角吗 你自己先试试看!
1.下列说法错误的是 ( )
A.∠AOB的顶点是O
B.∠AOB的边是两条射线
C.∠AOB与∠BOA表示同一个角
D.射线BO、射线AO分别是∠AOB的边
2.已知O是直线AB上一点,OC是一条射线,则∠AOC与∠BOC的关系是 ( )
A.∠AOC一定大于∠BOC
B.∠AOC一定小于∠BOC
C.∠AOC一定等于∠BOC
D.∠AOC可能大于、等于或小于∠BOC
3.如图,OC平分∠AOB,OD平分∠COB ( http: / / www.21cnjy.com ),∠AOB=x,则∠AOC= ,∠COD= ,∠AOD= + = .
( http: / / www.21cnjy.com )
4.3.2 角的度量与计算(1)
1.理解角的度量单位度、分、秒.
2.会进行角度的简单换算以及角的和、差计算.
一、 新知探究
阅读教材第126、127页的内容,自主探究,回答下列问题:
我们在测量长度时,要用到长 ( http: / / www.21cnjy.com )度单位如:千米、米、厘米、分米、毫米等;在测量重量时,要用到重量单位如:吨、千克、克等;在描述时间时,要用到时间单位如:年、月、日、时、分、秒.
1.每种单位之间都可以互 ( http: / / www.21cnjy.com )相换算,如:1千米=1 000 米,这里我们不妨把“千米”称为“大单位”,把“米”称为“小单位”,那么从“大单位”到“小单位”是如何换算的呢 请根据长度单位的换算关系写出你的理解和做法.
2.要度量角的大小就需要角的度量单位,请认真阅读教材,描述1°的概念.
3.角度单位的换算与时间单位的时、分、秒之间的换算是一致的,因此角度的基本度量单位之间的换算也是60进制,请你写出角度单位的换算关系.
4. 180度以内的角,可以按照角的大小分为哪三种角,请分别画图说明.
二、 基础演练
根据以上的探究,自主解决下列问题,并与小组成员交流分享你的学习成果:
1.两个锐角的和 ( )
A.一定为锐角
B.一定为钝角
C.一定为直角
D.可能是锐角或钝角或直角
2.若∠1=50°5',∠2=50.5°,则∠1和∠2的大小关系是 ( )
A.∠1=∠2 B.∠1>∠2
C.∠1<∠2 D.无法确定
3.阅读教材第126页例1、例2,完成下列题目.
(1)用度、分、秒表示32.36°;
(2)用度表示14°48'54″.
4.阅读教材第127页例3,仿做下题.
(1)77°42'+34°45';
(2)180°-56°23'18″.
三、 综合提升
先尝试独立解决,再与小组成员合作交流,解决下列问题:
1.观察钟面,1小时时针转 度;1分钟分针转 度,时针转 度.
2.求下列时刻时针与分针所成的角,并探索规律.
(1)8点整;
(2)6点30分;
(3)5点54分.
计算:
(1)用度、分、秒表示30.26°;
(2)用度表示35°25'48″;
(3)20°26'+35°54';
(4)90°-43°18'.
本课时主要学习了哪些知识与方法 有何收获和感悟 还有哪些疑惑
用数写的格言
1.王菊珍的百分数
我国科学家王菊珍对待实验失败有句格言,叫做“干下去还有50%成功的希望,不干便是100%的失败.”
2.托尔斯泰的分数
俄国大文豪托尔斯泰在谈到人的评价时,把 ( http: / / www.21cnjy.com )人比作一个分数.他说:“一个人就好像一个分数,他的实际才能好比分子,而他对自己的估价好比分母.分母越大,则分数的值就越小.”
3.雷巴柯夫的常数与变数
俄国历史学家雷巴柯夫在利用时间方面是这 ( http: / / www.21cnjy.com )样说的:“时间是个常数,但对勤奋者来说,是个‘变数’.用‘分’来计算时间的人比用‘小时’来计算时间的人时间多59倍.”
1.已知OC平分∠AOB,若∠BOC=29°34',则∠AOB= .
2.(1)用度、分、秒表示39.33°;
(2)用度表示65°25'12″.
3.计算:
(1)49°38'+66°22'26″;
(2)167°13'-79°48'35″.
4.已知钟表现在时刻为2:30,此时时针和分针所夹角的度数是多少
4.3.2 角的度量与计算(2)
1.知道余角、补角的概念,并会求一个角的余角或补角.
2.理解余角、补角的性质,并能通过它们的性质进行角的运算.
3.体会几何问题从观察、测量、探究向证明的转变.
一、 新知探究
通过阅读教材第128、129页,然后根据你对教材的理解,回答下列问题:
1.如果两个角互为余角,那么对这两个角的大小有怎样的要求,对它们的位置有要求吗
2.如果两个角互为补角,那么对这两个角的大小有怎样的要求,对它们的位置有要求吗
3.教材第128页的“探究”中谈到了“等量代换”的概念,你能用自己的话进行描述吗
4.教材第128页的“探究”中得出结论“同角(或等角)的补角相等”,你理解这句话的含义吗,试结合下图用几何语言进行描述.
5.“同角(或等角)的余角相等”,你理解这句话的含义吗,请结合下图用几何语言进行描述.
( http: / / www.21cnjy.com )
二、 基础演练
根据以上的探究,自主解决下列问题,并与小组成员交流分享你的学习成果:
1.(1)58°的余角是 ,补角是 ;
(2)105°25'的补角是 ;
(3)36°18'47″的余角是 ;
2.已知∠1和∠2互余,∠3和∠2互补,且有∠3=143°,则∠1= .
3.一个角的余角和补角也互为补角,这个角是 ( )
A. 30° B. 75°
C. 45° D. 15°
4.已知一个角比它的余角小15°,则这个角的补角是多少度
三、 综合提升
先尝试独立解决,再与小组成员合作交流,解决下列问题:
1.已知∠A=42°,则它的余角等于 ,补角等于 ,补角与余角的差等于 .
2.如图,O为直线AB上的一点,OM平分∠AOC,ON平分∠BOC,则图中互余的角共有 ( )
A. 1对
B. 2对
C. 3对
D. 4对
3.∠A的余角与∠A的补角互为补角,那么2∠A是 ( )
A.直角 B.锐角
C.钝角 D.以上三种都有可能
4.如图,已知AC为一条直线,O为直线AC上一点,且∠DOB=∠AOB,∠BOE=∠BOC,∠DOB与∠BOE互余,求∠AOB和∠BOC的度数.
1.一个角的补角是36°35',这个角的度数是 .
2.如图,点O在直线AB上,OC为射线,∠1比∠2的3倍少10°,则∠1和∠2的度数分别为 ( )
A.∠1=80°,∠2=100°
B.∠1=100°,∠2=80°
C.∠1=47.5°,∠2=132.5°
D.∠1=132.5°,∠2=47.5°
3.一个角的余角比它的补角的还少20°,求这个角的度数
本课时主要学习了哪些知识与方法 有何收获和感悟 还有哪些疑惑
数学谜语
(1)上午不上午,下午不下午,两针合一处,太阳猛似虎.(打一时刻)
(2)待命出发.(打一数学符号)
(3)一减一不是0.(打一数字)
(4)剃头(打一数学计算方法)
(5)停战(打一数学名称)
1.一个角的余角是53°47'25″,则这个角的补角的度数是 .
2.一个角等于它的补角的5倍,那么这个角的补角的余角是 ( )
A. 30° B. 60°
C. 45° D. 150°
3.已知一个角的补角是它余角的4倍,求这个角的度数.
4.如图,∠AOB=114°,OF是∠AOB的平分线,∠1与∠2互余,求∠1的度数.
同课章节目录
